4.2 平方根与立方根 第1课时 算术平方根(共24张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 4.2 平方根与立方根 第1课时 算术平方根(共24张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 10:47:46 | ||
图片预览






文档简介
(共24张PPT)
2 平方根与立方根
第1课时 算术平方根
第四章 实数
1.了解算术平方根的概念及其性质.
2.会求一个数的算术平方根.
学习目标
学校要举行美术作品比赛,小明很高兴,他想裁出一块面积为25的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?你能帮小明算一算吗?
身边小事
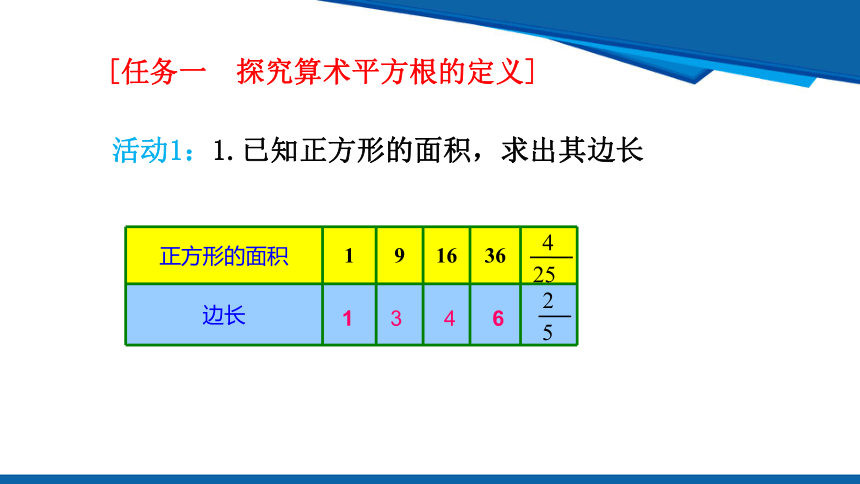
正方形的面积 1 9 16 36
边长
1
3
4
6
25
4
[任务一 探究算术平方根的定义]
活动1:1.已知正方形的面积,求出其边长
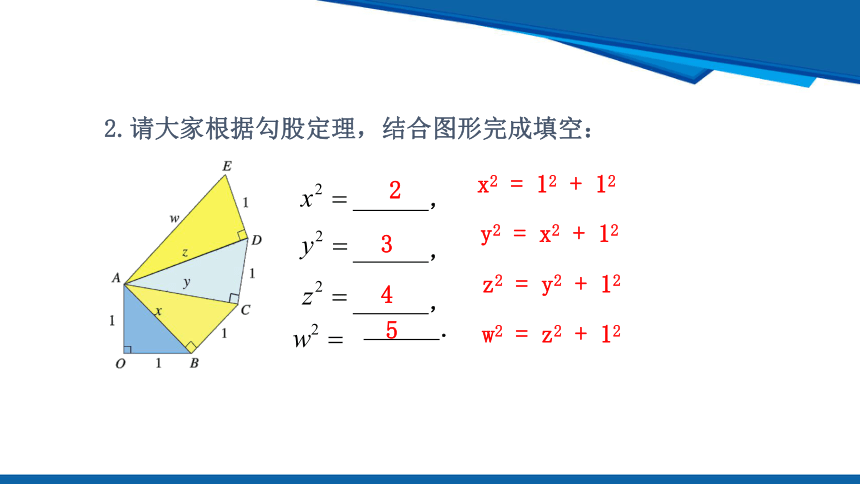
2.请大家根据勾股定理,结合图形完成填空:
x2 = 12 + 12
,
,
,
.
2
3
4
5
y2 = x2 + 12
z2 = y2 + 12
w2 = z2 + 12
问题1:x,y,z,w中哪些是有理数 哪些是无理数
x,y,w是无理数,z是有理数.因为没有任何整数或分数的平方等于2,3,5,
所以x,y,w不是有理数,而=4,所以z=2,是有理数.
问题2:我们发现这些问题都是知道一个正数的平方,去找这个正数,引出定义.
算术平方根的定义:若一个正数x的平方等于a,即x2=a,则这个正数x就叫作a的算术平方根.记为“”,读作“根号a”.特别地,规定0的算术平方根是0,即 =0.
问题3:根据算术平方根是定义,你能表示x,y,z,w吗
x=,y=,z=,w=.
典
题
精
讲
例1 求下列各数的算术平方根:
(1)900;(2)1;(3) ;(4)14.
解:(1) 因为302=900,所以900的算术平方根是30,
即 ;
(2)因为12=1,所以1的算术平方根是1,即 ;
(3)因为 ,所以 的算术平方根是 ,
即 ;
(4)14的算术平方根是 .
1.的算术平方根等于( )
A.4 B.±4 C.2 D.±2
2.9的算术平方根为( )
A.﹣ B.3 C.﹣3 D.
3.算术平方根等于它本身的实数有 个.
4.若=5,则m的值是 .
5.若x+2的算术平方根是3,求3x+4的算术平方根.
即时测评
解:∵x+2的算术平方根是3,
∴x+2=9,
∴x=7,
∴3x+4=25,
∴3x+4的算术平方根为5.
C
B
2
25
问题1:在例1中,一些数的算术平方根的结果没了“”,这些数有什么持点?
这些数是一个非负数数的完全平方即中a≥0.
问题2:的结果能为负数吗?
不能,即≥0,
问题3:中a≥0且≥0(双重非负性).
问题4:在例1中,=30.也就是=30.一般地,当a≥0时,=a成立吗?
a≥0时,=a成立.
[任务二 探究算术平方根的性质]
活动2
问题5:思考当a<0时,=a成立吗?
不成立,当a<0时,=﹣a.
问题6:=a成立吗?这里的a是什么数?你是怎么理解的?与同伴交流.
=a成立,这里a≥0.
总结归纳:
(1)算术平方根的性质:一个正数的算术平方根是 ;0的算术平方根是0;
负数 算术平方根.
(2)式子的双重非负性:一是a≥0,二是
(3)=,=a(a≥0)。
一个正数
没有
例2 自由下落物体的高度h(米)与下落时间t(秒)的关系为h=4.9t2.有一铁球从19.6 米高的建筑物上自由下落,到达地面需要多长时间 ?
典例精讲
即时测评
1.∣2a-4∣=0,则a+b=( )
A.a+b=﹣1 B.a+b=1 C.a+b=2 D.a+b=3
2.已知+∣b+2∣=0,则的值为( )
A.0 B.±1 C.1 D.﹣1
3.若a,b为实数,且+=0,则(a+b)2025= .
B
C
-1
4.若实数m、n满足+=0等式,求2m+n的算术平方根.
解:∵+=0,
∴m﹣2=0,n+4=0,
∴m=2,n=﹣4,
∴2m+n=2×2﹣4=0,
∵0的算术平方根是0,
∴2m+n的算术平方根为0.
5.《清秘藏》是明代所著工艺美术鉴赏著作,其中所述的刺绣在中国经过长时间的发展,已经形成了极高的工艺水平和独特的工艺门类.现有一张长方形绣布,长、宽之比为4:3,绣布面积为588cm2,求绣布的周长。
解:设绣布的长为4x cm,宽为3x cm,根据题意,
得4x 3x=588,
即12x2=588,
∴x2=49,
∵x>0,∴x=7,
∴绣布的长为28cm,宽为21cm,周长为2×(28+21)=98(cm).
1.下列说法中,正确的是( )
A.一个数的算术平方根一定是正数 B.-4 的算术平方根是2
C.-7是的算术平方根 D.如果a﹤0,那么没有意义
2.一个数的算术平方根为,比这个数小3的数是( )
A. a-3 B.-3 C. +3 D.-3
3.2的算术平方根是 ,的算术平方根是 ,的算术平方根是 .
4.若与互为相反数,则的值为 .
5.若,则实数a的取值范围为 .
D
D
9
3
16
a≥0
6.求下列各式的值:
(1) (2) (3)-
解:(1) =1.2;
(2) =47;
(3)-=﹣=﹣
7.某小区准备修建一个面积为75m2的花坛,甲、乙两个工程队给出如下两个施工方案.
甲:花坛为长方形,且长与宽的比为3:1.
乙:花坛为正方形.
(1)求长方形花坛的宽.
(2)嘉淇说:“正方形花坛的边长肯定比长方形花坛的宽长3m.”请你判断嘉淇的说法是否正确,并通过计算说明.
解:(1)设长方形花坛的宽为x m,则长为3x m,
由题意得x 3x=3x2=75,
因此,x===5,
即长方形花坛的宽为5m.
(2)嘉淇的说法错误,理由如下:
由(1)知长方形花坛的宽为5米,
若嘉淇的说法正确,正方形花坛的边长为:5+3=8(m),
则正方形花坛的面积为:82=64(m2)≠75(m2),
因此假设不成立,即嘉淇的说法错误.
课堂总结
1.一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,则这个正数 x 就叫做 a 的算术平方根,记作“ ”,读作“根号 a ”.
特别地,我们规定:0 的算术平方根是0,即 .
2 算术平方根的性质:
非负数
算术平方根具有双重非负性
(a≥0)
基础题:1.课后随堂练习第3题
提高题:2.请学有余力的同学做课后习题第5,6题,下节课在班内展示、交流。
课后作业
本节课到此结束,谢谢大家!
2 平方根与立方根
第1课时 算术平方根
第四章 实数
1.了解算术平方根的概念及其性质.
2.会求一个数的算术平方根.
学习目标
学校要举行美术作品比赛,小明很高兴,他想裁出一块面积为25的正方形画布,画上自己的得意之作参加比赛,这块正方形画布的边长应取多少?你能帮小明算一算吗?
身边小事
正方形的面积 1 9 16 36
边长
1
3
4
6
25
4
[任务一 探究算术平方根的定义]
活动1:1.已知正方形的面积,求出其边长
2.请大家根据勾股定理,结合图形完成填空:
x2 = 12 + 12
,
,
,
.
2
3
4
5
y2 = x2 + 12
z2 = y2 + 12
w2 = z2 + 12
问题1:x,y,z,w中哪些是有理数 哪些是无理数
x,y,w是无理数,z是有理数.因为没有任何整数或分数的平方等于2,3,5,
所以x,y,w不是有理数,而=4,所以z=2,是有理数.
问题2:我们发现这些问题都是知道一个正数的平方,去找这个正数,引出定义.
算术平方根的定义:若一个正数x的平方等于a,即x2=a,则这个正数x就叫作a的算术平方根.记为“”,读作“根号a”.特别地,规定0的算术平方根是0,即 =0.
问题3:根据算术平方根是定义,你能表示x,y,z,w吗
x=,y=,z=,w=.
典
题
精
讲
例1 求下列各数的算术平方根:
(1)900;(2)1;(3) ;(4)14.
解:(1) 因为302=900,所以900的算术平方根是30,
即 ;
(2)因为12=1,所以1的算术平方根是1,即 ;
(3)因为 ,所以 的算术平方根是 ,
即 ;
(4)14的算术平方根是 .
1.的算术平方根等于( )
A.4 B.±4 C.2 D.±2
2.9的算术平方根为( )
A.﹣ B.3 C.﹣3 D.
3.算术平方根等于它本身的实数有 个.
4.若=5,则m的值是 .
5.若x+2的算术平方根是3,求3x+4的算术平方根.
即时测评
解:∵x+2的算术平方根是3,
∴x+2=9,
∴x=7,
∴3x+4=25,
∴3x+4的算术平方根为5.
C
B
2
25
问题1:在例1中,一些数的算术平方根的结果没了“”,这些数有什么持点?
这些数是一个非负数数的完全平方即中a≥0.
问题2:的结果能为负数吗?
不能,即≥0,
问题3:中a≥0且≥0(双重非负性).
问题4:在例1中,=30.也就是=30.一般地,当a≥0时,=a成立吗?
a≥0时,=a成立.
[任务二 探究算术平方根的性质]
活动2
问题5:思考当a<0时,=a成立吗?
不成立,当a<0时,=﹣a.
问题6:=a成立吗?这里的a是什么数?你是怎么理解的?与同伴交流.
=a成立,这里a≥0.
总结归纳:
(1)算术平方根的性质:一个正数的算术平方根是 ;0的算术平方根是0;
负数 算术平方根.
(2)式子的双重非负性:一是a≥0,二是
(3)=,=a(a≥0)。
一个正数
没有
例2 自由下落物体的高度h(米)与下落时间t(秒)的关系为h=4.9t2.有一铁球从19.6 米高的建筑物上自由下落,到达地面需要多长时间 ?
典例精讲
即时测评
1.∣2a-4∣=0,则a+b=( )
A.a+b=﹣1 B.a+b=1 C.a+b=2 D.a+b=3
2.已知+∣b+2∣=0,则的值为( )
A.0 B.±1 C.1 D.﹣1
3.若a,b为实数,且+=0,则(a+b)2025= .
B
C
-1
4.若实数m、n满足+=0等式,求2m+n的算术平方根.
解:∵+=0,
∴m﹣2=0,n+4=0,
∴m=2,n=﹣4,
∴2m+n=2×2﹣4=0,
∵0的算术平方根是0,
∴2m+n的算术平方根为0.
5.《清秘藏》是明代所著工艺美术鉴赏著作,其中所述的刺绣在中国经过长时间的发展,已经形成了极高的工艺水平和独特的工艺门类.现有一张长方形绣布,长、宽之比为4:3,绣布面积为588cm2,求绣布的周长。
解:设绣布的长为4x cm,宽为3x cm,根据题意,
得4x 3x=588,
即12x2=588,
∴x2=49,
∵x>0,∴x=7,
∴绣布的长为28cm,宽为21cm,周长为2×(28+21)=98(cm).
1.下列说法中,正确的是( )
A.一个数的算术平方根一定是正数 B.-4 的算术平方根是2
C.-7是的算术平方根 D.如果a﹤0,那么没有意义
2.一个数的算术平方根为,比这个数小3的数是( )
A. a-3 B.-3 C. +3 D.-3
3.2的算术平方根是 ,的算术平方根是 ,的算术平方根是 .
4.若与互为相反数,则的值为 .
5.若,则实数a的取值范围为 .
D
D
9
3
16
a≥0
6.求下列各式的值:
(1) (2) (3)-
解:(1) =1.2;
(2) =47;
(3)-=﹣=﹣
7.某小区准备修建一个面积为75m2的花坛,甲、乙两个工程队给出如下两个施工方案.
甲:花坛为长方形,且长与宽的比为3:1.
乙:花坛为正方形.
(1)求长方形花坛的宽.
(2)嘉淇说:“正方形花坛的边长肯定比长方形花坛的宽长3m.”请你判断嘉淇的说法是否正确,并通过计算说明.
解:(1)设长方形花坛的宽为x m,则长为3x m,
由题意得x 3x=3x2=75,
因此,x===5,
即长方形花坛的宽为5m.
(2)嘉淇的说法错误,理由如下:
由(1)知长方形花坛的宽为5米,
若嘉淇的说法正确,正方形花坛的边长为:5+3=8(m),
则正方形花坛的面积为:82=64(m2)≠75(m2),
因此假设不成立,即嘉淇的说法错误.
课堂总结
1.一般地,如果一个正数 x 的平方等于 a ,即 x2 = a,则这个正数 x 就叫做 a 的算术平方根,记作“ ”,读作“根号 a ”.
特别地,我们规定:0 的算术平方根是0,即 .
2 算术平方根的性质:
非负数
算术平方根具有双重非负性
(a≥0)
基础题:1.课后随堂练习第3题
提高题:2.请学有余力的同学做课后习题第5,6题,下节课在班内展示、交流。
课后作业
本节课到此结束,谢谢大家!
