4.2 平方根与立方根 第4课时 估算(共31张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 4.2 平方根与立方根 第4课时 估算(共31张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 10:50:21 | ||
图片预览









文档简介
(共31张PPT)
2 平方根与立方根
第4课时 估算
第四章 实数
1.会估算一个无理数的大致范围;
2.会利用估算的方法比较两个无理数的大小;
3.会利用估算解决一些简单的实际问题。
学习目标
小丽:“我想在一块面积为500cm 的正方形纸片中,沿着边的方向裁出一块面积为300cm 的长方形的纸片,使它的长是宽的2倍,不知能否裁出?”
小明:“用一块面积大的纸片裁出一块面积小的纸片,那肯定行.”
你同意小明的说法吗?小丽能否用这块纸片裁出符合要求的纸片呢?为什么?学习了下面的知识你就知道啦!
[任务一 探究估算的方法]
问题1:某地开辟了一块长方形的荒地,新建一个以环保为主题的公园.已知这块荒地的长是宽的2倍,它的面积为400 000 .
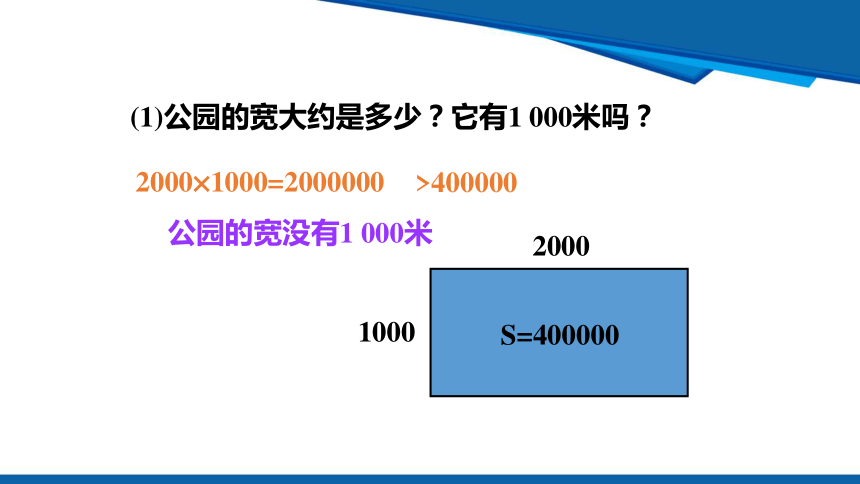
(1)公园的宽大约是多少 它有1 000 m吗
(2)如果要求误差小于10 m,它的宽大约是多少
(3)该公园中心有一个圆形花圃,它的面积是800 ,你能估计它的半径吗 (误差小于1 m)
活动1:阅读课本并解答下列问题
思考1:大家能不能具体确定一下公园的宽是几位数呢
思考2:公园的宽大约是几百米
思考3:再继续估算,估计十位上的数字是几
因为100的平方是10 000,1 000的平方是1 000 000,而200 000大于 10 000 小于1 000 000,所以公园的宽比100大而比1 000小,是三位数.
因为400的平方为160 000,500的平方为250 000,所以公园的宽应比400大比500小,所以公园的宽应为400多.
因为440的平方为193 600,450的平方为202 500,所以公园的宽应比440大比450小,故十位上的数字为4.因为题目要求误差小于10米,不是精确到十位,所以我们估算出十位上数就行了,即公园的宽应为440或450米.
(1)公园的宽大约是多少?它有1 000米吗?
1000
2000
S=400000
2000×1000=2000000
>400000
公园的宽没有1 000米
(2)如果要求误差小于10米,它的宽大约是多少?
x
2x
S=400000
x×2x=400000
2x2=400000
x2=200000
x=
怎样估算一个无理数的范围?
凭直觉,我们知道:
因为4002<20 0000<5002
所以 400< <500
所以 的百位数字是4
因为4402< 200000 <4502
所以440<<450
所以,的十位数字是4
因为 要求误差小于10米,
所以≈440或450
夹逼法
误差小于10 ,就是估算到什么位?
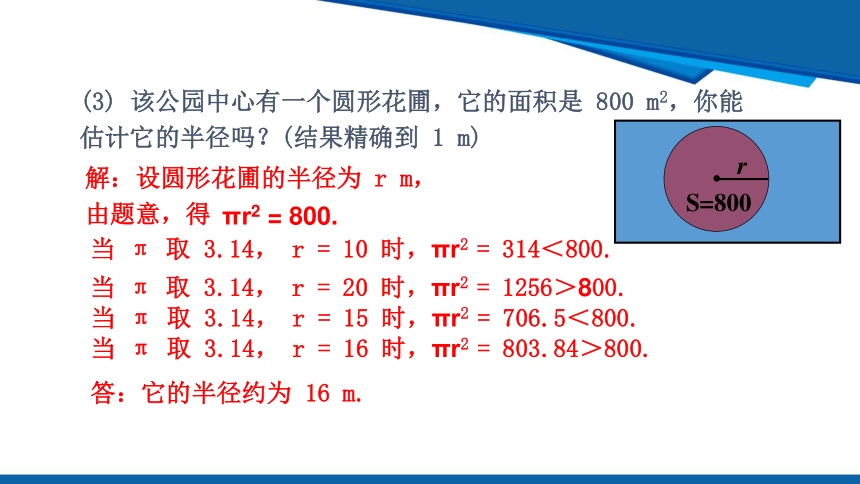
(3) 该公园中心有一个圆形花圃,它的面积是 800 m2,你能估计它的半径吗?(结果精确到 1 m)
解:设圆形花圃的半径为 r m,由题意,得
πr2 = 800.
当 π 取 3.14, r = 10 时,πr2 = 314<800.
当 π 取 3.14, r = 20 时,πr2 = 1256>800.
当 π 取 3.14, r = 15 时,πr2 = 706.5<800.
当 π 取 3.14, r = 16 时,πr2 = 803.84>800.
答:它的半径约为 16 m.
S=800
r
总结:估算的一般步骤
(1)估计是几位数.
(2)确定最高位上的数字(如百位).
(3)确定下一位上的数字(如十位).
(4)依次类推,直到确定出个位上的数,或者按要求精确到小数点后的某一位.
问题2:思考·交流:
(1)下列计算结果正确吗?你是怎样判断的?与同伴进行交流.
√
×
×
方法一:两数同时乘方
(2) 你能估算 的大小吗?(结果精确到1)
解:因为9.53=857.375,
103=1000,
所以9.5 < < 10,
所以 ≈ 10.
当 x = 10 时,x2 = 100> 88.
当 x = 9 时,x2 =81 < 88.
当 x = 9.5 时,x2 = 90.25 > 88.
当 x = 9.3 时,x2 = 86.49 <88.
所以 x = ≈ 9.4.
答:估计草坪的边长为9.4m.
(3)校园里有一块面积是88正方形草坪,试估计草坪的边长(结果精确到0.1m)
当 x = 9.4 时,x2 = 88.36 > 88.
生活经验表明,靠墙摆放梯子时,
若梯子底端离墙距离为梯子长度的
三分之一,则梯子比较稳定.现有一
长度为6 m的梯子,当梯子稳定摆放
时,他的顶端最多能到达5.6m高的
墙头吗 ?
典例精讲
解:设梯子稳定摆放时所能达到的的高度为x m,
此时梯子底端离墙恰好为梯子长度的 ,根
据勾股定理,有
6
A
B
C
所以
因此,当梯子稳定摆放时,它的顶端能够达到5.6米的墙头。
即时测评
1.估计-2的值在( )
A.4到5之间 B.3到4之间 C.2到3之间 D.1到2之间
2.若一个正方形的面积是8,则估计它的边长大小在( )
A.2与2.5之间 B.2.5与3之间
C.3与3.5之间 D.3.5与4之间
3.m、n是连续的两个整数,若m<<n,则m+n的值为 .
4.规定用[m]表示一个实数m的整数部分,例如[]=0,[3.14]=3.按此规定[-+1]的值为 .
C
B
7
-4
(1)宽与长之比是的长方形称为“黄金矩形”,通过估算,通过估算,你能比较 与 的大小吗?你是怎样想的?与同伴进行交流.
(2)小明是这样想的: 与 的分母相同,只要比较它们的分子就可以了.因为 >2,所以 -1>1,因此 >.
你认为小明的想法正确吗
正确
[任务二 探究通过估算比较大小]
活动2:
比较两个无理数大小的常用方法:
1.估算法:估算出所给无理数的近似值,再比较.
2.作差法:若 ,则 ;若 ,
则 .
3.乘方法:把含根号的两个无理数同时乘方(一般平方或立方),比较乘方后的数的大小,同时考虑符号确定大小即可.
4.放缩法:将其中一个数(或两个数)放大或缩小,再比较.
5.作商法、倒数法等.
总结
例2通过估算,你能比较与的大小吗?说说你的理由.
典例精讲
解:<,理由如下:
因为1<<2,
所以-1<1,
所以<
1.下列各式比较大小正确的是( )
A.-<- B.﹣>﹣
C.﹣π<﹣3.14 D.->-3
2.比较大小: .
3.比较大小:6 3.
即时测评
C
<
>
4.比较下列各组数的大小:
(1)与6;
(2)与﹣3;
(3)-1与.
解:因为1<<2,
所以<
-1<2,
所以 -1>
解:(1)∵<,
∴<6;
(2)∵>,
∴>﹣3;
1. 的值在( )
A.1与 2 之间 B.2 与 3 之间
C.3 与 4 之间 D.5 与 6 之间
C
2.下列式子成立的是( )
A. >2.5 B. <
C. < 3.85 D. -1<
D
3.如果设4-的整数部分为a,则a的值为 .
4.比较大小 .
5.已知<a<,且a是整数,则a的值是 .
2
<
3
6.一个人每天平均要饮用大约0.001 5 m3的各种液体,按70岁计算,他所饮用的液体总量大约为40m3.如果用一圆柱形的容器(底面直径等于高)来装这些液体,这个容器大约有多高 (结果精确到1m)
解:设容器的高大约为h m.
h3≈51,h≈ .
因为 ,所以这个容器的高大约为4m.
通过本节课的学习,你有哪些收获?
1、 “误差小于1”与“精确到1” 意义不同。
2、学会了用“夹逼法”估算无理数的大小。
3、学会了怎样比较两个实数的大小。
基础题:1.课后习题第2题
提高题:2.请学有余力的同学做课后习题第4、5题,下节课在班内展示、交流。
课后作业
本节课到此结束,谢谢大家!
2 平方根与立方根
第4课时 估算
第四章 实数
1.会估算一个无理数的大致范围;
2.会利用估算的方法比较两个无理数的大小;
3.会利用估算解决一些简单的实际问题。
学习目标
小丽:“我想在一块面积为500cm 的正方形纸片中,沿着边的方向裁出一块面积为300cm 的长方形的纸片,使它的长是宽的2倍,不知能否裁出?”
小明:“用一块面积大的纸片裁出一块面积小的纸片,那肯定行.”
你同意小明的说法吗?小丽能否用这块纸片裁出符合要求的纸片呢?为什么?学习了下面的知识你就知道啦!
[任务一 探究估算的方法]
问题1:某地开辟了一块长方形的荒地,新建一个以环保为主题的公园.已知这块荒地的长是宽的2倍,它的面积为400 000 .
(1)公园的宽大约是多少 它有1 000 m吗
(2)如果要求误差小于10 m,它的宽大约是多少
(3)该公园中心有一个圆形花圃,它的面积是800 ,你能估计它的半径吗 (误差小于1 m)
活动1:阅读课本并解答下列问题
思考1:大家能不能具体确定一下公园的宽是几位数呢
思考2:公园的宽大约是几百米
思考3:再继续估算,估计十位上的数字是几
因为100的平方是10 000,1 000的平方是1 000 000,而200 000大于 10 000 小于1 000 000,所以公园的宽比100大而比1 000小,是三位数.
因为400的平方为160 000,500的平方为250 000,所以公园的宽应比400大比500小,所以公园的宽应为400多.
因为440的平方为193 600,450的平方为202 500,所以公园的宽应比440大比450小,故十位上的数字为4.因为题目要求误差小于10米,不是精确到十位,所以我们估算出十位上数就行了,即公园的宽应为440或450米.
(1)公园的宽大约是多少?它有1 000米吗?
1000
2000
S=400000
2000×1000=2000000
>400000
公园的宽没有1 000米
(2)如果要求误差小于10米,它的宽大约是多少?
x
2x
S=400000
x×2x=400000
2x2=400000
x2=200000
x=
怎样估算一个无理数的范围?
凭直觉,我们知道:
因为4002<20 0000<5002
所以 400< <500
所以 的百位数字是4
因为4402< 200000 <4502
所以440<<450
所以,的十位数字是4
因为 要求误差小于10米,
所以≈440或450
夹逼法
误差小于10 ,就是估算到什么位?
(3) 该公园中心有一个圆形花圃,它的面积是 800 m2,你能估计它的半径吗?(结果精确到 1 m)
解:设圆形花圃的半径为 r m,由题意,得
πr2 = 800.
当 π 取 3.14, r = 10 时,πr2 = 314<800.
当 π 取 3.14, r = 20 时,πr2 = 1256>800.
当 π 取 3.14, r = 15 时,πr2 = 706.5<800.
当 π 取 3.14, r = 16 时,πr2 = 803.84>800.
答:它的半径约为 16 m.
S=800
r
总结:估算的一般步骤
(1)估计是几位数.
(2)确定最高位上的数字(如百位).
(3)确定下一位上的数字(如十位).
(4)依次类推,直到确定出个位上的数,或者按要求精确到小数点后的某一位.
问题2:思考·交流:
(1)下列计算结果正确吗?你是怎样判断的?与同伴进行交流.
√
×
×
方法一:两数同时乘方
(2) 你能估算 的大小吗?(结果精确到1)
解:因为9.53=857.375,
103=1000,
所以9.5 < < 10,
所以 ≈ 10.
当 x = 10 时,x2 = 100> 88.
当 x = 9 时,x2 =81 < 88.
当 x = 9.5 时,x2 = 90.25 > 88.
当 x = 9.3 时,x2 = 86.49 <88.
所以 x = ≈ 9.4.
答:估计草坪的边长为9.4m.
(3)校园里有一块面积是88正方形草坪,试估计草坪的边长(结果精确到0.1m)
当 x = 9.4 时,x2 = 88.36 > 88.
生活经验表明,靠墙摆放梯子时,
若梯子底端离墙距离为梯子长度的
三分之一,则梯子比较稳定.现有一
长度为6 m的梯子,当梯子稳定摆放
时,他的顶端最多能到达5.6m高的
墙头吗 ?
典例精讲
解:设梯子稳定摆放时所能达到的的高度为x m,
此时梯子底端离墙恰好为梯子长度的 ,根
据勾股定理,有
6
A
B
C
所以
因此,当梯子稳定摆放时,它的顶端能够达到5.6米的墙头。
即时测评
1.估计-2的值在( )
A.4到5之间 B.3到4之间 C.2到3之间 D.1到2之间
2.若一个正方形的面积是8,则估计它的边长大小在( )
A.2与2.5之间 B.2.5与3之间
C.3与3.5之间 D.3.5与4之间
3.m、n是连续的两个整数,若m<<n,则m+n的值为 .
4.规定用[m]表示一个实数m的整数部分,例如[]=0,[3.14]=3.按此规定[-+1]的值为 .
C
B
7
-4
(1)宽与长之比是的长方形称为“黄金矩形”,通过估算,通过估算,你能比较 与 的大小吗?你是怎样想的?与同伴进行交流.
(2)小明是这样想的: 与 的分母相同,只要比较它们的分子就可以了.因为 >2,所以 -1>1,因此 >.
你认为小明的想法正确吗
正确
[任务二 探究通过估算比较大小]
活动2:
比较两个无理数大小的常用方法:
1.估算法:估算出所给无理数的近似值,再比较.
2.作差法:若 ,则 ;若 ,
则 .
3.乘方法:把含根号的两个无理数同时乘方(一般平方或立方),比较乘方后的数的大小,同时考虑符号确定大小即可.
4.放缩法:将其中一个数(或两个数)放大或缩小,再比较.
5.作商法、倒数法等.
总结
例2通过估算,你能比较与的大小吗?说说你的理由.
典例精讲
解:<,理由如下:
因为1<<2,
所以-1<1,
所以<
1.下列各式比较大小正确的是( )
A.-<- B.﹣>﹣
C.﹣π<﹣3.14 D.->-3
2.比较大小: .
3.比较大小:6 3.
即时测评
C
<
>
4.比较下列各组数的大小:
(1)与6;
(2)与﹣3;
(3)-1与.
解:因为1<<2,
所以<
-1<2,
所以 -1>
解:(1)∵<,
∴<6;
(2)∵>,
∴>﹣3;
1. 的值在( )
A.1与 2 之间 B.2 与 3 之间
C.3 与 4 之间 D.5 与 6 之间
C
2.下列式子成立的是( )
A. >2.5 B. <
C. < 3.85 D. -1<
D
3.如果设4-的整数部分为a,则a的值为 .
4.比较大小 .
5.已知<a<,且a是整数,则a的值是 .
2
<
3
6.一个人每天平均要饮用大约0.001 5 m3的各种液体,按70岁计算,他所饮用的液体总量大约为40m3.如果用一圆柱形的容器(底面直径等于高)来装这些液体,这个容器大约有多高 (结果精确到1m)
解:设容器的高大约为h m.
h3≈51,h≈ .
因为 ,所以这个容器的高大约为4m.
通过本节课的学习,你有哪些收获?
1、 “误差小于1”与“精确到1” 意义不同。
2、学会了用“夹逼法”估算无理数的大小。
3、学会了怎样比较两个实数的大小。
基础题:1.课后习题第2题
提高题:2.请学有余力的同学做课后习题第4、5题,下节课在班内展示、交流。
课后作业
本节课到此结束,谢谢大家!
