5.2 平面直角坐标系 第1课时 平面直角坐标系(共24张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 5.2 平面直角坐标系 第1课时 平面直角坐标系(共24张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 10:56:00 | ||
图片预览







文档简介
(共24张PPT)
第五章 位置与坐标
2 平面直角坐标系
第1课时 平面直角坐标系
1.掌握平面直角坐标系及相关概念,会建立适当的直角坐标系;
2.会根据坐标轴描出点的位置,由点的位置写出它的坐标.
3.了解平面直角坐标系把平面分成四个象限,坐标轴不属于任何象限;
4.知道有序实数对与平面内的点的一一对应的关系。
学习目标
如图呈现了北京市部分景点的大致位置、小亮和来访的朋友位于卢沟桥、小亮如何向来访的朋友分绍图中各个最点的位置呢?
向东……,向北…….
[任务一:探究平面直角坐标系]
活动1:解答下列各题.
(1) 小亮在景点图上画上了方格,标上数字,并用 (0 , 0) 表示卢沟桥的位置,用 (11 , 4) 表示天安门广场的位置,那么北京奥林匹克公园的位置如何表示?(5 , 12) 表示哪个景点的位置?(6 , 5) 呢?
(11,12)
圆明园景点的位置
湘潭公园景点的位置
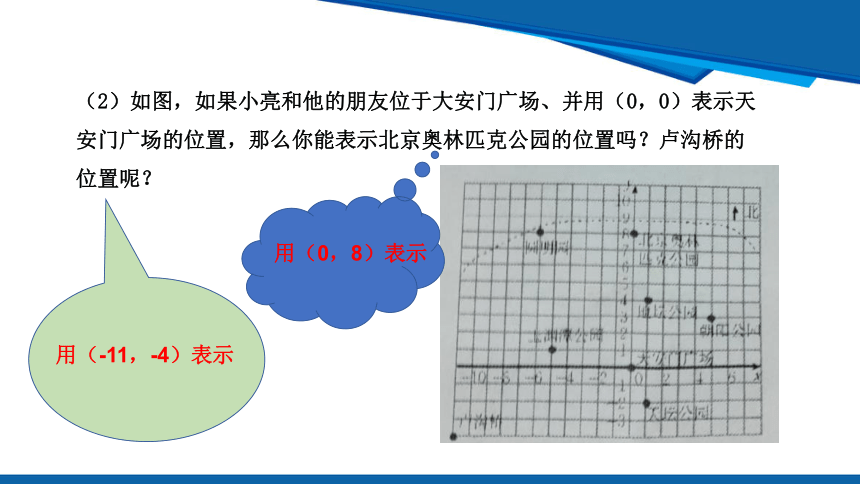
(2)如图,如果小亮和他的朋友位于大安门广场、并用(0,0)表示天安门广场的位置,那么你能表示北京奥林匹克公园的位置吗?卢沟桥的位置呢?
用(0,8)表示
用(-11,-4)表示
总结
1. 在平面内, 组成平面直角坐标系。
2.两条坐标轴:通常,两条数轴分别置于 位置与 位置,取向 或 的方向分别为两条数轴的正方向,水平的数轴称为 轴或 轴;铅直的数轴称为 轴或 轴.
3.两条数轴的公共原点叫作 .
4.这个平面叫 平面.
两条互相垂直且有公共原点的数轴
右
上
坐标
坐标原点
铅直
水平
x
横
y
纵
[任务二 探究点的坐标及象限]
活动2:解答下列问题.
问题1:对于平面内的某一点,如图中点M,怎样用一对有序实数来表示呢?
问题2:给出有序实数对(-3,2),
如何在直角坐标系中标出点A(-3,2)呢?
M(4,3)
如图,经过点M向X轴、y轴作垂线,垂足在x轴、y轴上上,对应的数是4,3分别叫作点M的横坐标、纵坐标;有序实数对(4,3)叫作点M的坐标.
追问:你能写出N、G、H、P的坐标吗?
问题3:在平面直角坐标系中,任意有序实数都对应着一个点吗?你是怎样得到这个点的?
N(3,4);G(2,-2);H(-2,1);P(-3,-3).
例如:经过x轴上对应的数为-3的点作x轴的垂线,经过y轴上对应的数为2的点作y轴的垂线,两条垂线的交点A就是和有序实数对(-3,2)相对应的点。同样,可以得到和有序实数对(2.5,-2)对应的点B,和有序实数对(2,1)对应的点C。
在平面直角坐标系中,对于任意一对有序实数对,都有平面上唯一的一点与它对应.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
y
纵轴
原点
x
横轴
第一象限
第二象限
第三象限
第四象限
注意:坐标轴上的点不属于任何象限。
追问:坐标轴上的点在象限内吗?
坐标轴上的点不在任何一个象限内.
例1 写出图中多边形ABCDEF各顶点的坐标.
典例精讲
解:如图,各个顶点的坐标分别为
A(-2,0)、B(0,-3)、C(3,-1)、D(4,0)、E(3,1)、F(0,3).
1.在如图所示的平面直角坐标系中:
(1)写出点A,B,C,D,E,F的坐标;
(2)描出下列各点:L(-5, -3),
M(4,0),N(0,5),P(6,2).
(1)A( -3,-2),B(-5,4),
C( 5, -4),D(0, -3 ),
E( 2,5),F(-3,0).
(2)描出各点如图.
即时测评
L
M
N
P
(1) 在下图所示的平面直角坐标系中, 描出下列各点:
A (-5 , 0),B (1 , 4 ),C (3 , 3),
D (1 , 0 ),E (3 , -3),F (1 , -4).
(2) 依次连接 A,B,C,D,E,F,A,你得到什么图形?
A
B
C
D
E
F
解:(1) 如图所示.
(2) 如图所示,图形像纸飞机.
[任务三 探究有序实数对与坐标平面内点的关系]
活动3:按要求解答下列问题.
(3) 在平面直角坐标系中,点与实数对之间有何关系?
在直角坐标系中,对于平面上的任意一点,都有唯一的一个有序实数对 (即点的坐标) 与它对应;
反过来,对于任意一个有序实数对,都有平面上唯一的一点与它对应.
1.2023年12月16日,“横跨”花溪、南明、云岩和乌当四区的贵阳地铁3号线正式开通运营.“北京路”是其中的一个换乘站,若以“北京路”为原点,建立如图所示的平面直角坐标系,若用表示“喷水池”,则可以表示“贵阳一中”的坐标是( )
A.(-7,1) B.(1,-7)
C.(-1,7) D.(7,1)
A
2.用(1,-2)可大致表示图中的( )
A.点E B.点F C.点 G D.点H
3.如下所示的图形中,平面直角坐标系的画法正确的有( ).
C
B
4.如图,在平面直角坐标系中完成以下问题:
(1)描出点A(-3,-2)、B(2,-2)、C(-2,1)、D(3,1),
并顺次连接点A,B,C,D;
(2)求四边形ABCD的面积.
解:(1)如图所示:
(2)解:AB=2-(-3)=2+3=5,
边上的高为3,
四边形ABCD的面积=5×3=15.
课堂总结
平面直角坐标系
定义:原点、坐标轴
点的坐标
定义与符号特征
描点
点的坐标的确定
布置作业
随堂练习P121,P122 T1~T3
本节课到此结束,谢谢大家!
第五章 位置与坐标
2 平面直角坐标系
第1课时 平面直角坐标系
1.掌握平面直角坐标系及相关概念,会建立适当的直角坐标系;
2.会根据坐标轴描出点的位置,由点的位置写出它的坐标.
3.了解平面直角坐标系把平面分成四个象限,坐标轴不属于任何象限;
4.知道有序实数对与平面内的点的一一对应的关系。
学习目标
如图呈现了北京市部分景点的大致位置、小亮和来访的朋友位于卢沟桥、小亮如何向来访的朋友分绍图中各个最点的位置呢?
向东……,向北…….
[任务一:探究平面直角坐标系]
活动1:解答下列各题.
(1) 小亮在景点图上画上了方格,标上数字,并用 (0 , 0) 表示卢沟桥的位置,用 (11 , 4) 表示天安门广场的位置,那么北京奥林匹克公园的位置如何表示?(5 , 12) 表示哪个景点的位置?(6 , 5) 呢?
(11,12)
圆明园景点的位置
湘潭公园景点的位置
(2)如图,如果小亮和他的朋友位于大安门广场、并用(0,0)表示天安门广场的位置,那么你能表示北京奥林匹克公园的位置吗?卢沟桥的位置呢?
用(0,8)表示
用(-11,-4)表示
总结
1. 在平面内, 组成平面直角坐标系。
2.两条坐标轴:通常,两条数轴分别置于 位置与 位置,取向 或 的方向分别为两条数轴的正方向,水平的数轴称为 轴或 轴;铅直的数轴称为 轴或 轴.
3.两条数轴的公共原点叫作 .
4.这个平面叫 平面.
两条互相垂直且有公共原点的数轴
右
上
坐标
坐标原点
铅直
水平
x
横
y
纵
[任务二 探究点的坐标及象限]
活动2:解答下列问题.
问题1:对于平面内的某一点,如图中点M,怎样用一对有序实数来表示呢?
问题2:给出有序实数对(-3,2),
如何在直角坐标系中标出点A(-3,2)呢?
M(4,3)
如图,经过点M向X轴、y轴作垂线,垂足在x轴、y轴上上,对应的数是4,3分别叫作点M的横坐标、纵坐标;有序实数对(4,3)叫作点M的坐标.
追问:你能写出N、G、H、P的坐标吗?
问题3:在平面直角坐标系中,任意有序实数都对应着一个点吗?你是怎样得到这个点的?
N(3,4);G(2,-2);H(-2,1);P(-3,-3).
例如:经过x轴上对应的数为-3的点作x轴的垂线,经过y轴上对应的数为2的点作y轴的垂线,两条垂线的交点A就是和有序实数对(-3,2)相对应的点。同样,可以得到和有序实数对(2.5,-2)对应的点B,和有序实数对(2,1)对应的点C。
在平面直角坐标系中,对于任意一对有序实数对,都有平面上唯一的一点与它对应.
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
y
纵轴
原点
x
横轴
第一象限
第二象限
第三象限
第四象限
注意:坐标轴上的点不属于任何象限。
追问:坐标轴上的点在象限内吗?
坐标轴上的点不在任何一个象限内.
例1 写出图中多边形ABCDEF各顶点的坐标.
典例精讲
解:如图,各个顶点的坐标分别为
A(-2,0)、B(0,-3)、C(3,-1)、D(4,0)、E(3,1)、F(0,3).
1.在如图所示的平面直角坐标系中:
(1)写出点A,B,C,D,E,F的坐标;
(2)描出下列各点:L(-5, -3),
M(4,0),N(0,5),P(6,2).
(1)A( -3,-2),B(-5,4),
C( 5, -4),D(0, -3 ),
E( 2,5),F(-3,0).
(2)描出各点如图.
即时测评
L
M
N
P
(1) 在下图所示的平面直角坐标系中, 描出下列各点:
A (-5 , 0),B (1 , 4 ),C (3 , 3),
D (1 , 0 ),E (3 , -3),F (1 , -4).
(2) 依次连接 A,B,C,D,E,F,A,你得到什么图形?
A
B
C
D
E
F
解:(1) 如图所示.
(2) 如图所示,图形像纸飞机.
[任务三 探究有序实数对与坐标平面内点的关系]
活动3:按要求解答下列问题.
(3) 在平面直角坐标系中,点与实数对之间有何关系?
在直角坐标系中,对于平面上的任意一点,都有唯一的一个有序实数对 (即点的坐标) 与它对应;
反过来,对于任意一个有序实数对,都有平面上唯一的一点与它对应.
1.2023年12月16日,“横跨”花溪、南明、云岩和乌当四区的贵阳地铁3号线正式开通运营.“北京路”是其中的一个换乘站,若以“北京路”为原点,建立如图所示的平面直角坐标系,若用表示“喷水池”,则可以表示“贵阳一中”的坐标是( )
A.(-7,1) B.(1,-7)
C.(-1,7) D.(7,1)
A
2.用(1,-2)可大致表示图中的( )
A.点E B.点F C.点 G D.点H
3.如下所示的图形中,平面直角坐标系的画法正确的有( ).
C
B
4.如图,在平面直角坐标系中完成以下问题:
(1)描出点A(-3,-2)、B(2,-2)、C(-2,1)、D(3,1),
并顺次连接点A,B,C,D;
(2)求四边形ABCD的面积.
解:(1)如图所示:
(2)解:AB=2-(-3)=2+3=5,
边上的高为3,
四边形ABCD的面积=5×3=15.
课堂总结
平面直角坐标系
定义:原点、坐标轴
点的坐标
定义与符号特征
描点
点的坐标的确定
布置作业
随堂练习P121,P122 T1~T3
本节课到此结束,谢谢大家!
