6.1 函数(共38张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 6.1 函数(共38张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 10:59:59 | ||
图片预览





文档简介
(共38张PPT)
第六章 一次函数
1 函数
学习目标
1.经历函数概念的抽象概括过程,体会函数概念,能判断两个变量间的关系是否可看作函数。
2.初步形成函数的观点、认识现实世界的意识和能力。
你坐在摩天轮上,随着时间的变化,你离开地面的高度是如何变化的?
由低变高,再由高变低.
O 1 2 3 4 5 6 7 8 9 10 11 12
h(米)
t(分)
[任务一 探究两个变量关系的三种表示方法]
活动1
O 1 2 3 4 5 6 7 8 9 10 11 12
3
h(米)
t(分)
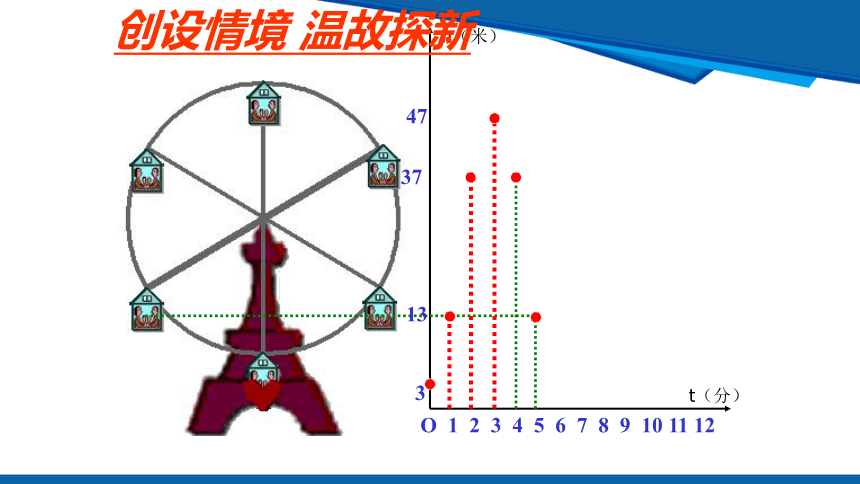
创设情境 温故探新
O 1 2 3 4 5 6 7 8 9 10 11 12
3
13
37
h(米)
t(分)
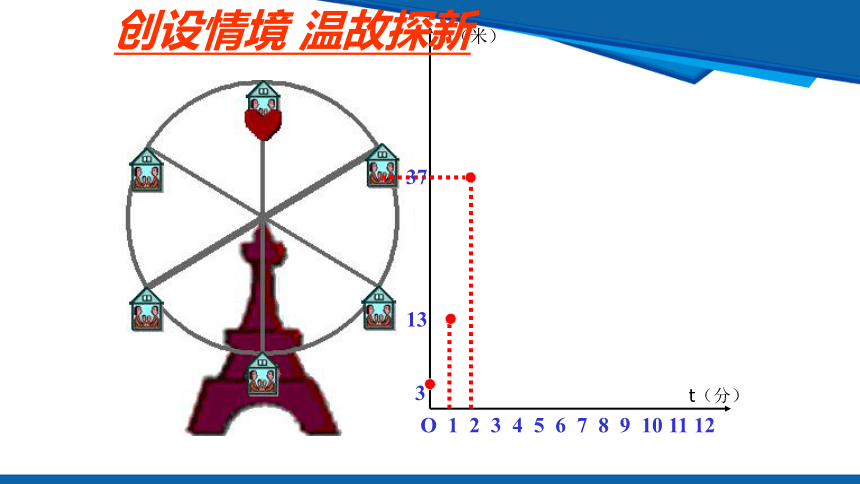
创设情境 温故探新
O 1 2 3 4 5 6 7 8 9 10 11 12
3
13
37
47
h(米)
t(分)
创设情境 温故探新
O 1 2 3 4 5 6 7 8 9 10 11 12
3
13
37
47
h(米)
t(分)
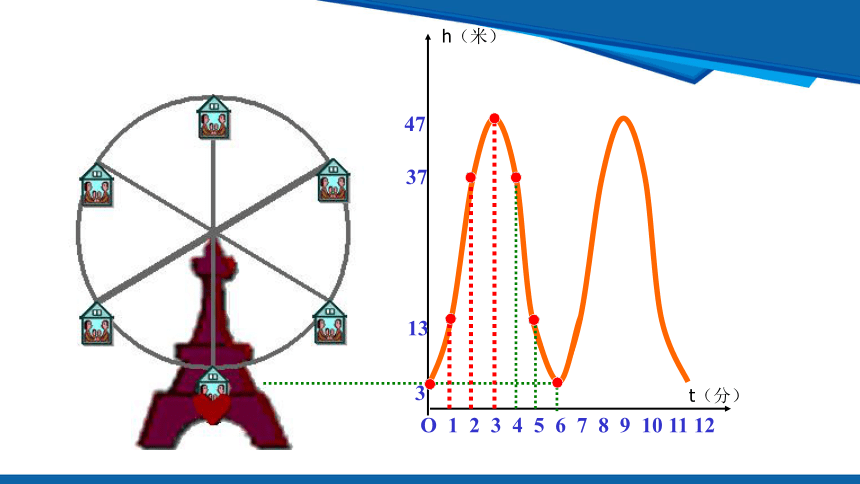
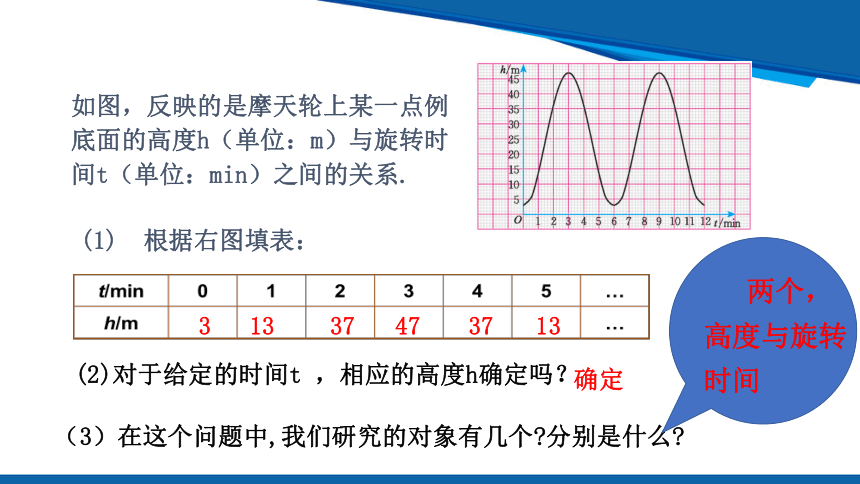
如图,反映的是摩天轮上某一点例底面的高度h(单位:m)与旋转时间t(单位:min)之间的关系.
(1) 根据右图填表:
3
13
37
47
37
13
(2)对于给定的时间t ,相应的高度h确定吗?
确定
(3)在这个问题中,我们研究的对象有几个 分别是什么
两个,
高度与旋转 时间
圆柱形的物体如下图堆放.随着层数的增加,物体的总数是如何变化的
填写下表:
1
3
6
10
15
思考? 层数n和物体总数y之间是什么关系
活动2
一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
(1)当t分别等于-43 ℃ ,-27 ℃ ,0 ℃ ,18 ℃时,相应的热力学温度T是多少?
活动3
解:当t=﹣43 ℃时,T=﹣43+273=230(K);
当t=﹣27 ℃时,T=﹣27+273=246(K);
当t=0 ℃时,T=0+273=273(K);
当t=18 ℃时,T=18+273=291(K).
思考: 在关系式T=t+273中,两个变量中若知道其中一个,是否可以确定另外一个
可以
(2)给定一个大于-273 ℃的t值,你能求出相应的T值吗?
将t的值代入关系式中,可求得T值
思考: 在关系式T=t+273中,两个变量中若知道其中一个,是否可以确定另外一个
可以
(2)给定一个大于-273 ℃的t值,你能求出相应的T值吗?
将t的值代入关系式中,可求得T值
1.(1)汽车在公路上匀速行驶,速度为每小时30千米,则汽车行驶的路程s(千米)与行驶的时间t(时)之间的关系式为 .
(2)圆的面积S与半径R的关系式为 .
2.某30层的大厦底层高4米,以上每层高3米,从底层数起,则前n层的高度h(米)与n的函数关系式为 .
即时测评
s=30t
S=πR2
h=3n+1
3.豌豆苗的呼吸作用强度受温度影响很大,观察图,回答问题:
(1)说明哪个量是自变量,哪个量是自变量的函数.
(2)温度在什么范围内时豌豆苗的呼吸作用强度逐渐变强?在什么范围内逐渐减弱?温度对豌豆苗的呼吸作用强度的影响.
即时测评
(1)此图反映的自变量是温度,呼吸作用强度是温度的函数;
(2)由图象知,温度在0℃到35℃范围内时豌豆苗的呼吸作用强度逐渐变强;在35℃到50℃范围内逐渐减弱.
上面的三个问题中,有什么共同特点?
①时间 t 、高度 h ;
②层数n、物体总数y;
③摄氏温度t、热力学温度T。
都有两个变量。
[任务二 探究函数的定义]
给定其中某一个变量的值,相应地就确定了另一个变量的值
活动4
(1)函数的定义:一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有 的值与它对应,那么我们称y是x的函数(function)、其x是 、y是 。
一个x值
一个y值
y就是x的函数
对应
总结:
即:
(2)函数的表示方法: 、 和 。
唯一
自变量
因变量
图象法
列表法
表达式法
典例精析
例1下列各曲线中,表示y是x的函数的是( )
D
A.
B.
C.
D.
即时测评
1.下列各图象中,y是x的函数的是( )
A
A.
B.
C.
D.
即时测评
2.圆的周长公式C=2πR中,有 个变量,
是 ,自变量是 ,因变量是 。
两
R、C
R
C
上述的三个问题中,要使函数有意义,自变量能取哪些值
同桌探究一下吧
注意:对于实际问题中,自变量的取值应使实际问题有意义。
[任务三 探究函数自变量取值范围及函数值]
活动5
(1)自变量 t 的取值范围: ;
(2)自变量 n 的取值范围: ;
(3)自变量t的取值范围:___________.
t≥0
n取正整数
t≥-273℃
总结:
对于自变量在可取值范围内的一个 的值 a,函数有 确定的对应值,这个对应值称为当自变量等于a 时的 .
确定
唯一
函数值
反馈练习巩固新知
指出下列变化关系中,哪些y是x的函数?哪些不是?
①xy=2;②x2+y2=10;
③x+y=5;④∣y∣=3x+1;
⑤y=x2-4x+5
解:①是,②不是,③是,
④不是,⑤是
1.下列曲线中,不能表示y是x的函数的是( )
A. B.
C. D.
D
2.如图是护士统计一位甲型H1N1流感疑似病人的体温变化图,这位病人在16时的体温约是( )
A.37.8℃ B.38℃
C.38.7℃ D.39.1℃
C
3.在利用太阳能热水器来加热水的过程中,热水器里的水温随所晒时间的长短而变化,这个问题中因变量是( )
A.太阳光强弱 B.水的温度 C.所晒时间 D.热水器
4.变量x与y之间的关系是y=x2﹣1,当自变量x=2时,因变量y的值是( )
A.﹣2 B.﹣1 C.1 D.2
B
C
5.如果两个变量x、y之间的函数关系如图所示,则自变量x的取值范围是 .
﹣3≤x≤3
6.我们解答过一些求代数式的值的题目,请把下面的问题补充完整:
当x的值分别取﹣5、0、1…时,3x2﹣2x+4的值分别为89、4、5…根据函数的定义,可以把x看做自变量,把 看做因变量,那么因变量 (填“是”或“不是”)自变量x的函数,理由是 .
代数式的值,
是
对于自变量每取一个值,因变量都有唯一确定的值与它对应.
7.在男子1000米的长跑中,运动员的平均速度v=,则这个关系式中自变量是 .
t
8.大家知道:“距离地面越远,温度越低”.小明查阅资料得到下面表格中的对应数据:
距离地面高度h/km 0 1 2 3 4 5 …
温度T/℃ 20 14 8 2 ﹣4 ﹣10 …
根据表中,请你帮助小明解决下列问题:
(1)根据表格中的数据发现:距离地面高度每升高1km,温度就降低 ℃,进而猜想:温度T与距离地面高度h之间的函数关系式为 .
(2)当h=10km时,高空的温度T是多少?
(3)当T=﹣28℃时,距离地面的高度h是多少?
(3)估计岩层10km深处的温度是多少.
8.解:(1)6,T=20﹣6h;
(2)由(1)得:T=20﹣6×10=﹣40(℃),
答:当h=10km时,高空的温度T是﹣40℃;
(3)当T=﹣28℃时,则:﹣28=20﹣6h,
解得:h=8.
1、函数的概念
2、函数的表示方法:
3、函数的自变量的取值范围.
4、函数值的求法—代入法
(1)图象法
(2)列表法
(3)关系式法
课堂小结
基础题:1.课后习题第 2题
提高题:2.请学有余力的同学采取合理的方式,搜集整理与本节课有关的“好题”,被选中的同学下节课为全班展示。
课后作业
本节课到此结束,谢谢大家!
第六章 一次函数
1 函数
学习目标
1.经历函数概念的抽象概括过程,体会函数概念,能判断两个变量间的关系是否可看作函数。
2.初步形成函数的观点、认识现实世界的意识和能力。
你坐在摩天轮上,随着时间的变化,你离开地面的高度是如何变化的?
由低变高,再由高变低.
O 1 2 3 4 5 6 7 8 9 10 11 12
h(米)
t(分)
[任务一 探究两个变量关系的三种表示方法]
活动1
O 1 2 3 4 5 6 7 8 9 10 11 12
3
h(米)
t(分)
创设情境 温故探新
O 1 2 3 4 5 6 7 8 9 10 11 12
3
13
37
h(米)
t(分)
创设情境 温故探新
O 1 2 3 4 5 6 7 8 9 10 11 12
3
13
37
47
h(米)
t(分)
创设情境 温故探新
O 1 2 3 4 5 6 7 8 9 10 11 12
3
13
37
47
h(米)
t(分)
如图,反映的是摩天轮上某一点例底面的高度h(单位:m)与旋转时间t(单位:min)之间的关系.
(1) 根据右图填表:
3
13
37
47
37
13
(2)对于给定的时间t ,相应的高度h确定吗?
确定
(3)在这个问题中,我们研究的对象有几个 分别是什么
两个,
高度与旋转 时间
圆柱形的物体如下图堆放.随着层数的增加,物体的总数是如何变化的
填写下表:
1
3
6
10
15
思考? 层数n和物体总数y之间是什么关系
活动2
一定质量的气体在体积不变时,假若温度降低到-273℃,则气体的压强为零.因此,物理学把-273℃作为热力学温度的零度.热力学温度T(K)与摄氏温度t(℃)之间有如下数量关系:T=t+273,T≥0.
(1)当t分别等于-43 ℃ ,-27 ℃ ,0 ℃ ,18 ℃时,相应的热力学温度T是多少?
活动3
解:当t=﹣43 ℃时,T=﹣43+273=230(K);
当t=﹣27 ℃时,T=﹣27+273=246(K);
当t=0 ℃时,T=0+273=273(K);
当t=18 ℃时,T=18+273=291(K).
思考: 在关系式T=t+273中,两个变量中若知道其中一个,是否可以确定另外一个
可以
(2)给定一个大于-273 ℃的t值,你能求出相应的T值吗?
将t的值代入关系式中,可求得T值
思考: 在关系式T=t+273中,两个变量中若知道其中一个,是否可以确定另外一个
可以
(2)给定一个大于-273 ℃的t值,你能求出相应的T值吗?
将t的值代入关系式中,可求得T值
1.(1)汽车在公路上匀速行驶,速度为每小时30千米,则汽车行驶的路程s(千米)与行驶的时间t(时)之间的关系式为 .
(2)圆的面积S与半径R的关系式为 .
2.某30层的大厦底层高4米,以上每层高3米,从底层数起,则前n层的高度h(米)与n的函数关系式为 .
即时测评
s=30t
S=πR2
h=3n+1
3.豌豆苗的呼吸作用强度受温度影响很大,观察图,回答问题:
(1)说明哪个量是自变量,哪个量是自变量的函数.
(2)温度在什么范围内时豌豆苗的呼吸作用强度逐渐变强?在什么范围内逐渐减弱?温度对豌豆苗的呼吸作用强度的影响.
即时测评
(1)此图反映的自变量是温度,呼吸作用强度是温度的函数;
(2)由图象知,温度在0℃到35℃范围内时豌豆苗的呼吸作用强度逐渐变强;在35℃到50℃范围内逐渐减弱.
上面的三个问题中,有什么共同特点?
①时间 t 、高度 h ;
②层数n、物体总数y;
③摄氏温度t、热力学温度T。
都有两个变量。
[任务二 探究函数的定义]
给定其中某一个变量的值,相应地就确定了另一个变量的值
活动4
(1)函数的定义:一般地,如果在一个变化过程中有两个变量x和y,并且对于变量x的每一个值,变量y都有 的值与它对应,那么我们称y是x的函数(function)、其x是 、y是 。
一个x值
一个y值
y就是x的函数
对应
总结:
即:
(2)函数的表示方法: 、 和 。
唯一
自变量
因变量
图象法
列表法
表达式法
典例精析
例1下列各曲线中,表示y是x的函数的是( )
D
A.
B.
C.
D.
即时测评
1.下列各图象中,y是x的函数的是( )
A
A.
B.
C.
D.
即时测评
2.圆的周长公式C=2πR中,有 个变量,
是 ,自变量是 ,因变量是 。
两
R、C
R
C
上述的三个问题中,要使函数有意义,自变量能取哪些值
同桌探究一下吧
注意:对于实际问题中,自变量的取值应使实际问题有意义。
[任务三 探究函数自变量取值范围及函数值]
活动5
(1)自变量 t 的取值范围: ;
(2)自变量 n 的取值范围: ;
(3)自变量t的取值范围:___________.
t≥0
n取正整数
t≥-273℃
总结:
对于自变量在可取值范围内的一个 的值 a,函数有 确定的对应值,这个对应值称为当自变量等于a 时的 .
确定
唯一
函数值
反馈练习巩固新知
指出下列变化关系中,哪些y是x的函数?哪些不是?
①xy=2;②x2+y2=10;
③x+y=5;④∣y∣=3x+1;
⑤y=x2-4x+5
解:①是,②不是,③是,
④不是,⑤是
1.下列曲线中,不能表示y是x的函数的是( )
A. B.
C. D.
D
2.如图是护士统计一位甲型H1N1流感疑似病人的体温变化图,这位病人在16时的体温约是( )
A.37.8℃ B.38℃
C.38.7℃ D.39.1℃
C
3.在利用太阳能热水器来加热水的过程中,热水器里的水温随所晒时间的长短而变化,这个问题中因变量是( )
A.太阳光强弱 B.水的温度 C.所晒时间 D.热水器
4.变量x与y之间的关系是y=x2﹣1,当自变量x=2时,因变量y的值是( )
A.﹣2 B.﹣1 C.1 D.2
B
C
5.如果两个变量x、y之间的函数关系如图所示,则自变量x的取值范围是 .
﹣3≤x≤3
6.我们解答过一些求代数式的值的题目,请把下面的问题补充完整:
当x的值分别取﹣5、0、1…时,3x2﹣2x+4的值分别为89、4、5…根据函数的定义,可以把x看做自变量,把 看做因变量,那么因变量 (填“是”或“不是”)自变量x的函数,理由是 .
代数式的值,
是
对于自变量每取一个值,因变量都有唯一确定的值与它对应.
7.在男子1000米的长跑中,运动员的平均速度v=,则这个关系式中自变量是 .
t
8.大家知道:“距离地面越远,温度越低”.小明查阅资料得到下面表格中的对应数据:
距离地面高度h/km 0 1 2 3 4 5 …
温度T/℃ 20 14 8 2 ﹣4 ﹣10 …
根据表中,请你帮助小明解决下列问题:
(1)根据表格中的数据发现:距离地面高度每升高1km,温度就降低 ℃,进而猜想:温度T与距离地面高度h之间的函数关系式为 .
(2)当h=10km时,高空的温度T是多少?
(3)当T=﹣28℃时,距离地面的高度h是多少?
(3)估计岩层10km深处的温度是多少.
8.解:(1)6,T=20﹣6h;
(2)由(1)得:T=20﹣6×10=﹣40(℃),
答:当h=10km时,高空的温度T是﹣40℃;
(3)当T=﹣28℃时,则:﹣28=20﹣6h,
解得:h=8.
1、函数的概念
2、函数的表示方法:
3、函数的自变量的取值范围.
4、函数值的求法—代入法
(1)图象法
(2)列表法
(3)关系式法
课堂小结
基础题:1.课后习题第 2题
提高题:2.请学有余力的同学采取合理的方式,搜集整理与本节课有关的“好题”,被选中的同学下节课为全班展示。
课后作业
本节课到此结束,谢谢大家!
