6.4 一次函数的应用 第2课时 一次函数的实际应用(共34张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 6.4 一次函数的应用 第2课时 一次函数的实际应用(共34张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 00:00:00 | ||
图片预览







文档简介
(共34张PPT)
4 一次函数的应用
第2课时 一次函数的实际应用
1.能通过函数图象获取信息,发展形象思维。
2.能利用函数图象解决简单的实际问题。
3.初步体会方程与函数的关系。
学习目标
温故知新
1.确定一次函数表达式需要几个条件?
2个
2.确定一次函数表示式的步骤是什么?
①设——设函数表达式y=kx+b;
②代——将点的坐标代入y=kx+b中,列出关于k、b的方程;
③求——解方程,求k、b;
④写——把求出的k、b值代回到表达式中即可
在前几节课里,我们分别学习了一次函数、一次函数的图象、一次函数图象的特征,并且了解到一次函数的应用十分广泛,和我们日常生活密切相关,因此本节课我们一起来学习一次函数的应用.
一起走进我们今天的学习.
某种摩托车的油箱加满油后,油箱中的剩余油量y(单位:L)与摩托车行驶路程x(单位:km)之间的关系如图所示.根据图象回答下列问题:(1)油箱最多可储油多少升?
x/千米
y/升
2
1
4
3
6
5
8
7
10
9
100
200
300
400
500
0
(2)一箱汽油可供摩托车行 驶多少千米?
解:(1)根据图象可知,当x=0时,y=10,故油箱最多可储油10升,
答:油箱最多可储油10升
(2)观察图象,得:
当y=0时,x=500.因此一箱汽油可供摩托车行驶500千米。
[任务一 探究从函数图象获取信息解决问题]
x/千米
y/升
2
1
4
3
6
5
8
7
10
9
100
200
300
400
500
0
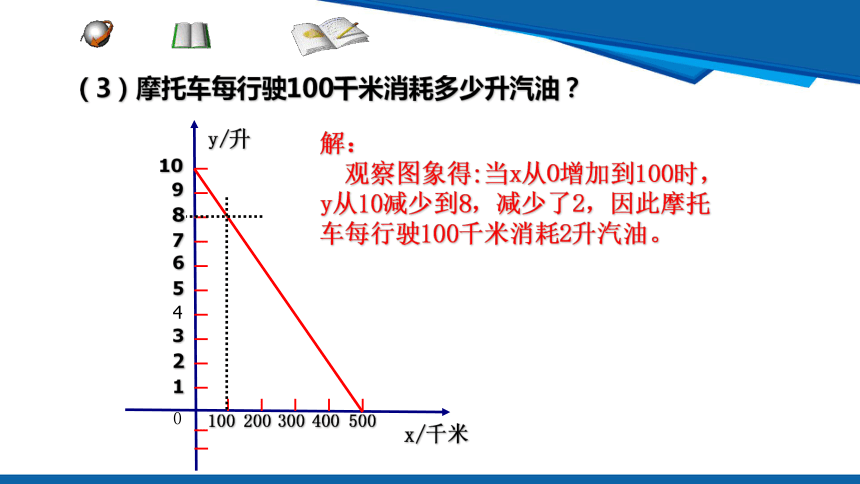
(3)摩托车每行驶100千米消耗多少升汽油?
解:
观察图象得:当x从0增加到100时,y从10减少到8,减少了2,因此摩托车每行驶100千米消耗2升汽油。
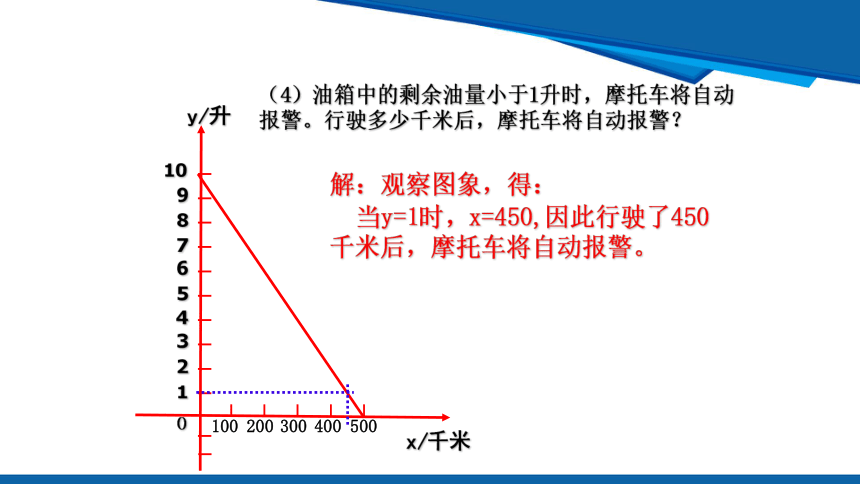
(4)油箱中的剩余油量小于1升时,摩托车将自动报警。行驶多少千米后,摩托车将自动报警?
x/千米
y/升
2
1
4
3
6
5
8
7
10
9
100
200
300
400
500
0
解:观察图象,得:
当y=1时,x=450,因此行驶了450千米后,摩托车将自动报警。
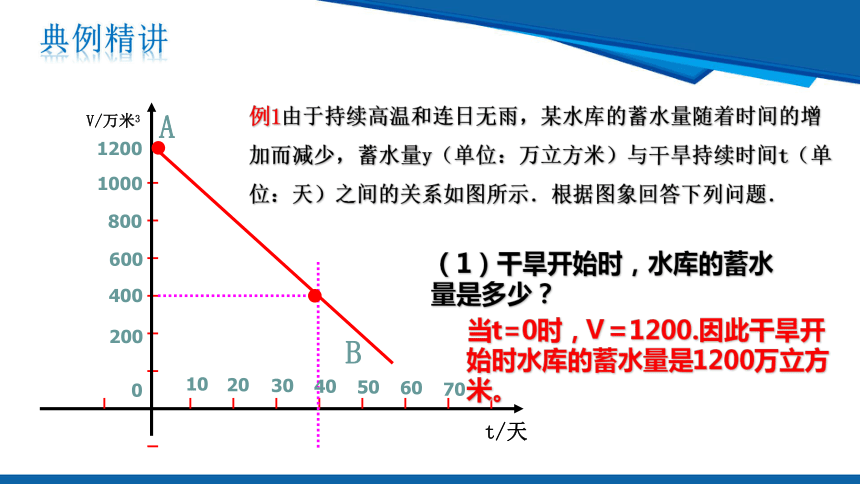
例1由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少,蓄水量y(单位:万立方米)与干旱持续时间t(单位:天)之间的关系如图所示.根据图象回答下列问题.
(1)干旱开始时,水库的蓄水量是多少?
A
t/天
V/万米3
200
400
600
800
1000
1200
10
20
30
40
50
60
70
0
B
典例精讲
当t=0时,V=1200.因此干旱开始时水库的蓄水量是1200万立方米。
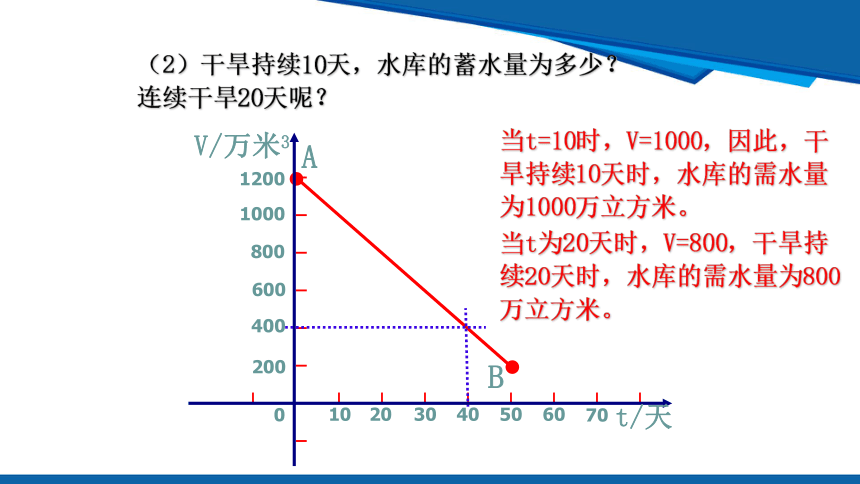
(2)干旱持续10天,水库的蓄水量为多少?连续干旱20天呢?
A
t/天
V/万米3
200
400
600
800
1000
1200
10
20
30
40
50
60
70
0
B
当t=10时,V=1000,因此,干旱持续10天时,水库的需水量为1000万立方米。
当t为20天时,V=800,干旱持续20天时,水库的需水量为800万立方米。
(3)蓄水量小于400万立方米时,将发生严重干旱警报,干旱持续约多少天后将发生严重干旱警报?
A
t/天
V/万米3
200
400
600
800
1000
1200
10
20
30
40
50
60
70
0
B
合作探究
当V=400万时,所t≈40,因此干旱持续约40天后将发生严重干旱警报。
问题1:干旱开始时,t的值是多少?
t=0
问题2:求干旱持续10天时的蓄水量,也就是求t等于多少时所对应的V的值?
求干旱持续10天时的蓄水量,也就是求t等于10时所对应的V的值。
问题3:当蓄水量小于400万立方米时,将发出严重干旱警报,也就是当V等于400万立方米时,求哪个变量的值?
所对应t的值
思考?按照这个规律,预计干旱持续多少天水库将干涸?你是怎么判断的.
预计持续干旱60天,水库将干涸.根据图象可知,蓄水池的水从第10天到第20天,蓄水池的水量从1000降到800,每天的降水量为(1000-800)÷10=20万立方米,第40天时蓄水池的水量是400万立方米,400÷20=20(天),即再有20天蓄水池干涸,所以预计干旱持续60天水库将干涸.
1.小亮意识到节水的重要性.当天在全校倡议节约用水,得到全校师生的积极响应.
从宣传活动开始,每天参加该活动的家庭数数量不断增加,
假设每天参加该活动的家庭数增加数量相同,
最后全校师生都参加了活动,并且参加该活动的家庭数(户)
与宣传时间(天)的函数关系如图所示.
根据图象回答下列问题:
即时测评
·
200
10000
20 t(天)
S(户)
0
(1)活动开始当天,全校有多少户家庭参加了该活动?
(2)全校师生共有多少户?该活动持续了几天?
(3)你知道平均每天增加了多少户?
(4)活动第几天时,参加该活动的家庭数达到600户?
即时测评
200
1000 20
设s=kt+b,将(0,200),(20,1000)代入
解得b=200,k=40,所以s=40t+200
所以平均每天增加40户.
600=40t+200,得t=10。
问题1:一元一次方程-20x+1200=0与一次函数y=-20x+1200有什么联系?
一元一次方程-20x+1200=0的解为x=60,一次函数y=-20x+1200的函数值为0时,相应的自变量的值为x=60。
问题2:你发现方程的解与函数与x轴交点的横坐标有什么关系?
一次函数y=-20x+1200与x轴交点的横坐标即为方程0.5x+1=0的解。
思考?一元一次方程kx+b=0的解与一次所数y=kx+b与x轴交点的横坐标都有这样的联系吗 与同伴进行交流。
一般地,当一次函数y=kx+b的函数值为0时,相应的白变量的值就是方程=kx+b=0的解,从图象上看,一次函数y=kx+b与x轴交点的横坐标就是方程kx+b=0的解.
[任务二 探究一次函数与一元一次方程的关系]
例2已知一次函数y=﹣x+2.
(1)求该直线与坐标轴的交点坐标;
(2)画出一次函数的图象;
(3)由图可知,若方程﹣x+2=0,
则方程的解为 .
[任务二 探究一次函数与一元一次方程的关系]
解:(1)x=0时,y=2,
y=0时,x=4,
则直线与x轴交点为(4,0),与y轴交点为(0,2);
(2)过点(4,0)与点(0,2)作直线,即为一次函数y=﹣x+2的图象;
(3)x=4.
1. 从“数”的方面看,当一次函数y=kx+b的函数值y=__时,相应的自变量的值即为方程kx+b=0的__ .
2. 从“形”的方面看,函数y=kx+b与x轴交点的_____即为方程kx+b=0的____.
归纳
0
解
横坐标
解
1.若直线y=kx﹣b经过点(﹣2,0),则关于x的方程kx﹣b=0的解是( )
A.2 B.﹣b C.﹣2 D.k
2.若一次函数y=kx+b(k≠0)的图象如图,则方程kx+b=0的解是 .
3.一次函数y=kx+b(k≠0)中两个变量
x,y的部分对应值如表所示:
那么关于x的方程kx+b=7的解是 .
即时测评
x … ﹣4 ﹣3 ﹣2 ﹣1 0 …
y … 9 7 5 3 1 …
C
x=2
x=﹣3
4.如图,根据一次函数y=kx+b的图象,直接写出下列问题的答案:
(1)关于x的方程kx+b=0的解;
(2)当x=1时,代数式kx+b的值;
(3)关于x的方程kx+b=﹣3的解.
解:(1)当x=2时,y=0,
所以方程kx+b=0的解为x=2;
(2)当x=1时,y=﹣1,
所以代数式kx+b的值为﹣1;
(3)当x=﹣1时,y=﹣3,
所以方程kx+b=﹣3的解为x=﹣1.
即时测评
1.如图,一次函数y=kx+b(k<0)的图象经过点A,则方程kx+b=3的解是( )
A.x=b B.x=2 C.x=3 D.
2.如图,一次函数y=kx+b(k≠0)
的图象经过点(﹣2,0),
则下列说法正确的是( )
A.k<0
B.b<0
C.y随x的增大而减小
D.方程kx+b=0的解是x=﹣2
B
D
3.生物活动小组的同学们观察某植物生长,得到该植物高度y(cm)与观察时间x(天)的关系,画出如图所示的函数图象(CD∥x轴).则该植物最高长到 cm.
31
4.爱好数学研究的依依同学受《乌鸦喝水》故事的启发,在学习完一次函数后,利用未装满水的容器和体积相同的小球(实心小铁球)进行了一次小游戏,她发现壁厚均匀的圆柱形容器的总高度为50cm,里面装有一定量的水,未放小球前测得水面高度为20cm,她将这些体积相同的小球逐个放入容器中,观察发现容器中水面高度y(cm)与她放入容器中的小球个数x(个)之间的关系如图所示.根据图中信息,解答下列问题:
(1)求图中AB段y与x之间的函数关系式;(无需写出自变量x的取值范围)
(2)当水面高度为40cm时,求依依放入容器中的小球个数.
解:(1)设图中AB段y与x之间的函数关系式为y=kx+b,
把(0,20)代入y=kx+b,得,b=20,
把(15,50)代入y=kx+b,得,
∴k=2
∴y=2x+20;
(2)在y=2x+20中,当y=2x+20=40时,x=10,
∴依依放入容器中的小球个数为10个.
5.汽车出发前油箱有油50L,行驶若干小时后,在加油站加油若干升.图象表示的是从出发后,油箱中剩余油量y(L)与行驶时间t(h)之间的关系.
(1)汽车行驶 h后加油,中途加油 L;
3
31
(2)求加油前油箱剩余油量y与行驶时间t的函数关系式;
解:设y与t的函数关系式y=kt+b(k、b为常数,且k≠0).
将坐标(0,50)代入y=kt+b,得b=50,
把(3,14)代入y=kt+b,得3k+b=14,
解得k=﹣12,
∴y与t的函数关系式y=﹣12t+50(0≤t≤3).
(3)已知加油前、后汽车都以70km/h匀速行驶,如果加油站距目的地280km,那么要到达目的地,油箱中的油是否够用?请说明理由.
解:要到达目的地,油箱中的油不够用.理由如下:
280÷70=4(h),
12×4=48(L),
∵45<48,
∴要到达目的地,油箱中的油不够用.
这节课你有哪些收获
1.从函数图象获取信息解决问题
2.一次函数与一元一次方程的关系
基础题:1.课后习题第 1题
提高题:2.请学有余力的同学做课后习题第 3题,下节课在全班展示、交流。
课后作业
课后作业
P163 随堂练习;
习题6.7 第1题
4 一次函数的应用
第2课时 一次函数的实际应用
1.能通过函数图象获取信息,发展形象思维。
2.能利用函数图象解决简单的实际问题。
3.初步体会方程与函数的关系。
学习目标
温故知新
1.确定一次函数表达式需要几个条件?
2个
2.确定一次函数表示式的步骤是什么?
①设——设函数表达式y=kx+b;
②代——将点的坐标代入y=kx+b中,列出关于k、b的方程;
③求——解方程,求k、b;
④写——把求出的k、b值代回到表达式中即可
在前几节课里,我们分别学习了一次函数、一次函数的图象、一次函数图象的特征,并且了解到一次函数的应用十分广泛,和我们日常生活密切相关,因此本节课我们一起来学习一次函数的应用.
一起走进我们今天的学习.
某种摩托车的油箱加满油后,油箱中的剩余油量y(单位:L)与摩托车行驶路程x(单位:km)之间的关系如图所示.根据图象回答下列问题:(1)油箱最多可储油多少升?
x/千米
y/升
2
1
4
3
6
5
8
7
10
9
100
200
300
400
500
0
(2)一箱汽油可供摩托车行 驶多少千米?
解:(1)根据图象可知,当x=0时,y=10,故油箱最多可储油10升,
答:油箱最多可储油10升
(2)观察图象,得:
当y=0时,x=500.因此一箱汽油可供摩托车行驶500千米。
[任务一 探究从函数图象获取信息解决问题]
x/千米
y/升
2
1
4
3
6
5
8
7
10
9
100
200
300
400
500
0
(3)摩托车每行驶100千米消耗多少升汽油?
解:
观察图象得:当x从0增加到100时,y从10减少到8,减少了2,因此摩托车每行驶100千米消耗2升汽油。
(4)油箱中的剩余油量小于1升时,摩托车将自动报警。行驶多少千米后,摩托车将自动报警?
x/千米
y/升
2
1
4
3
6
5
8
7
10
9
100
200
300
400
500
0
解:观察图象,得:
当y=1时,x=450,因此行驶了450千米后,摩托车将自动报警。
例1由于持续高温和连日无雨,某水库的蓄水量随着时间的增加而减少,蓄水量y(单位:万立方米)与干旱持续时间t(单位:天)之间的关系如图所示.根据图象回答下列问题.
(1)干旱开始时,水库的蓄水量是多少?
A
t/天
V/万米3
200
400
600
800
1000
1200
10
20
30
40
50
60
70
0
B
典例精讲
当t=0时,V=1200.因此干旱开始时水库的蓄水量是1200万立方米。
(2)干旱持续10天,水库的蓄水量为多少?连续干旱20天呢?
A
t/天
V/万米3
200
400
600
800
1000
1200
10
20
30
40
50
60
70
0
B
当t=10时,V=1000,因此,干旱持续10天时,水库的需水量为1000万立方米。
当t为20天时,V=800,干旱持续20天时,水库的需水量为800万立方米。
(3)蓄水量小于400万立方米时,将发生严重干旱警报,干旱持续约多少天后将发生严重干旱警报?
A
t/天
V/万米3
200
400
600
800
1000
1200
10
20
30
40
50
60
70
0
B
合作探究
当V=400万时,所t≈40,因此干旱持续约40天后将发生严重干旱警报。
问题1:干旱开始时,t的值是多少?
t=0
问题2:求干旱持续10天时的蓄水量,也就是求t等于多少时所对应的V的值?
求干旱持续10天时的蓄水量,也就是求t等于10时所对应的V的值。
问题3:当蓄水量小于400万立方米时,将发出严重干旱警报,也就是当V等于400万立方米时,求哪个变量的值?
所对应t的值
思考?按照这个规律,预计干旱持续多少天水库将干涸?你是怎么判断的.
预计持续干旱60天,水库将干涸.根据图象可知,蓄水池的水从第10天到第20天,蓄水池的水量从1000降到800,每天的降水量为(1000-800)÷10=20万立方米,第40天时蓄水池的水量是400万立方米,400÷20=20(天),即再有20天蓄水池干涸,所以预计干旱持续60天水库将干涸.
1.小亮意识到节水的重要性.当天在全校倡议节约用水,得到全校师生的积极响应.
从宣传活动开始,每天参加该活动的家庭数数量不断增加,
假设每天参加该活动的家庭数增加数量相同,
最后全校师生都参加了活动,并且参加该活动的家庭数(户)
与宣传时间(天)的函数关系如图所示.
根据图象回答下列问题:
即时测评
·
200
10000
20 t(天)
S(户)
0
(1)活动开始当天,全校有多少户家庭参加了该活动?
(2)全校师生共有多少户?该活动持续了几天?
(3)你知道平均每天增加了多少户?
(4)活动第几天时,参加该活动的家庭数达到600户?
即时测评
200
1000 20
设s=kt+b,将(0,200),(20,1000)代入
解得b=200,k=40,所以s=40t+200
所以平均每天增加40户.
600=40t+200,得t=10。
问题1:一元一次方程-20x+1200=0与一次函数y=-20x+1200有什么联系?
一元一次方程-20x+1200=0的解为x=60,一次函数y=-20x+1200的函数值为0时,相应的自变量的值为x=60。
问题2:你发现方程的解与函数与x轴交点的横坐标有什么关系?
一次函数y=-20x+1200与x轴交点的横坐标即为方程0.5x+1=0的解。
思考?一元一次方程kx+b=0的解与一次所数y=kx+b与x轴交点的横坐标都有这样的联系吗 与同伴进行交流。
一般地,当一次函数y=kx+b的函数值为0时,相应的白变量的值就是方程=kx+b=0的解,从图象上看,一次函数y=kx+b与x轴交点的横坐标就是方程kx+b=0的解.
[任务二 探究一次函数与一元一次方程的关系]
例2已知一次函数y=﹣x+2.
(1)求该直线与坐标轴的交点坐标;
(2)画出一次函数的图象;
(3)由图可知,若方程﹣x+2=0,
则方程的解为 .
[任务二 探究一次函数与一元一次方程的关系]
解:(1)x=0时,y=2,
y=0时,x=4,
则直线与x轴交点为(4,0),与y轴交点为(0,2);
(2)过点(4,0)与点(0,2)作直线,即为一次函数y=﹣x+2的图象;
(3)x=4.
1. 从“数”的方面看,当一次函数y=kx+b的函数值y=__时,相应的自变量的值即为方程kx+b=0的__ .
2. 从“形”的方面看,函数y=kx+b与x轴交点的_____即为方程kx+b=0的____.
归纳
0
解
横坐标
解
1.若直线y=kx﹣b经过点(﹣2,0),则关于x的方程kx﹣b=0的解是( )
A.2 B.﹣b C.﹣2 D.k
2.若一次函数y=kx+b(k≠0)的图象如图,则方程kx+b=0的解是 .
3.一次函数y=kx+b(k≠0)中两个变量
x,y的部分对应值如表所示:
那么关于x的方程kx+b=7的解是 .
即时测评
x … ﹣4 ﹣3 ﹣2 ﹣1 0 …
y … 9 7 5 3 1 …
C
x=2
x=﹣3
4.如图,根据一次函数y=kx+b的图象,直接写出下列问题的答案:
(1)关于x的方程kx+b=0的解;
(2)当x=1时,代数式kx+b的值;
(3)关于x的方程kx+b=﹣3的解.
解:(1)当x=2时,y=0,
所以方程kx+b=0的解为x=2;
(2)当x=1时,y=﹣1,
所以代数式kx+b的值为﹣1;
(3)当x=﹣1时,y=﹣3,
所以方程kx+b=﹣3的解为x=﹣1.
即时测评
1.如图,一次函数y=kx+b(k<0)的图象经过点A,则方程kx+b=3的解是( )
A.x=b B.x=2 C.x=3 D.
2.如图,一次函数y=kx+b(k≠0)
的图象经过点(﹣2,0),
则下列说法正确的是( )
A.k<0
B.b<0
C.y随x的增大而减小
D.方程kx+b=0的解是x=﹣2
B
D
3.生物活动小组的同学们观察某植物生长,得到该植物高度y(cm)与观察时间x(天)的关系,画出如图所示的函数图象(CD∥x轴).则该植物最高长到 cm.
31
4.爱好数学研究的依依同学受《乌鸦喝水》故事的启发,在学习完一次函数后,利用未装满水的容器和体积相同的小球(实心小铁球)进行了一次小游戏,她发现壁厚均匀的圆柱形容器的总高度为50cm,里面装有一定量的水,未放小球前测得水面高度为20cm,她将这些体积相同的小球逐个放入容器中,观察发现容器中水面高度y(cm)与她放入容器中的小球个数x(个)之间的关系如图所示.根据图中信息,解答下列问题:
(1)求图中AB段y与x之间的函数关系式;(无需写出自变量x的取值范围)
(2)当水面高度为40cm时,求依依放入容器中的小球个数.
解:(1)设图中AB段y与x之间的函数关系式为y=kx+b,
把(0,20)代入y=kx+b,得,b=20,
把(15,50)代入y=kx+b,得,
∴k=2
∴y=2x+20;
(2)在y=2x+20中,当y=2x+20=40时,x=10,
∴依依放入容器中的小球个数为10个.
5.汽车出发前油箱有油50L,行驶若干小时后,在加油站加油若干升.图象表示的是从出发后,油箱中剩余油量y(L)与行驶时间t(h)之间的关系.
(1)汽车行驶 h后加油,中途加油 L;
3
31
(2)求加油前油箱剩余油量y与行驶时间t的函数关系式;
解:设y与t的函数关系式y=kt+b(k、b为常数,且k≠0).
将坐标(0,50)代入y=kt+b,得b=50,
把(3,14)代入y=kt+b,得3k+b=14,
解得k=﹣12,
∴y与t的函数关系式y=﹣12t+50(0≤t≤3).
(3)已知加油前、后汽车都以70km/h匀速行驶,如果加油站距目的地280km,那么要到达目的地,油箱中的油是否够用?请说明理由.
解:要到达目的地,油箱中的油不够用.理由如下:
280÷70=4(h),
12×4=48(L),
∵45<48,
∴要到达目的地,油箱中的油不够用.
这节课你有哪些收获
1.从函数图象获取信息解决问题
2.一次函数与一元一次方程的关系
基础题:1.课后习题第 1题
提高题:2.请学有余力的同学做课后习题第 3题,下节课在全班展示、交流。
课后作业
课后作业
P163 随堂练习;
习题6.7 第1题
