问题解决策略:特殊化(共23张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 问题解决策略:特殊化(共23张PPT) 2025-2026学年数学鲁教版(五四制)七年级上册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
问题解决策略:特殊化
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
已知甲校学生数是乙校学生数的百分之四十,甲校女生数是甲校学生数的百分之三十,乙校男生数是乙校学生数的百分之四十二,那么两校女生总数占两校学生总数的百分之几
面对一般性问题时,可以先考虑特殊情形,借助特殊情形
下获得的结论或方法解决一般性问题,这就是特殊化策略。
一般性问题
一般性问题解决
特殊化
特殊问题
推广到
新知初探
贰
讲授新知
探究一:问题解决策略-特殊化
贰
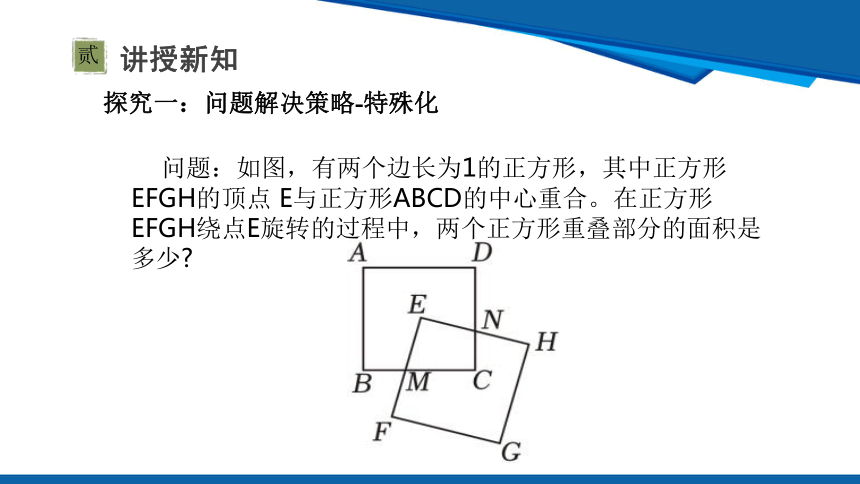
问题:如图,有两个边长为1的正方形,其中正方形EFGH的顶点 E与正方形ABCD的中心重合。在正方形 EFGH绕点E旋转的过程中,两个正方形重叠部分的面积是多少
理解问题
(1)在旋转的过程中,两个正方形的重叠部分会呈现出哪些情形
(2)对于这些不同的情形,如何求两个正方形重叠部分的面积?你遇到的困难是什么?
拟定计划
(1)哪些特殊情形下,两个正方形重叠部分的面积容易求出?
(2)其他情形能转化为容易求解的特殊情形吗?
实施计划
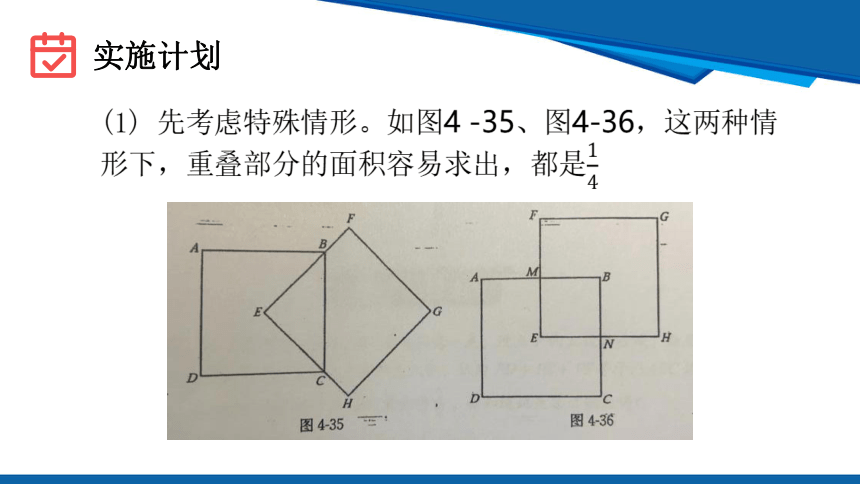
(1) 先考虑特殊情形。如图4 -35、图4-36,这两种情形下,重叠部分的面积容易求出,都是
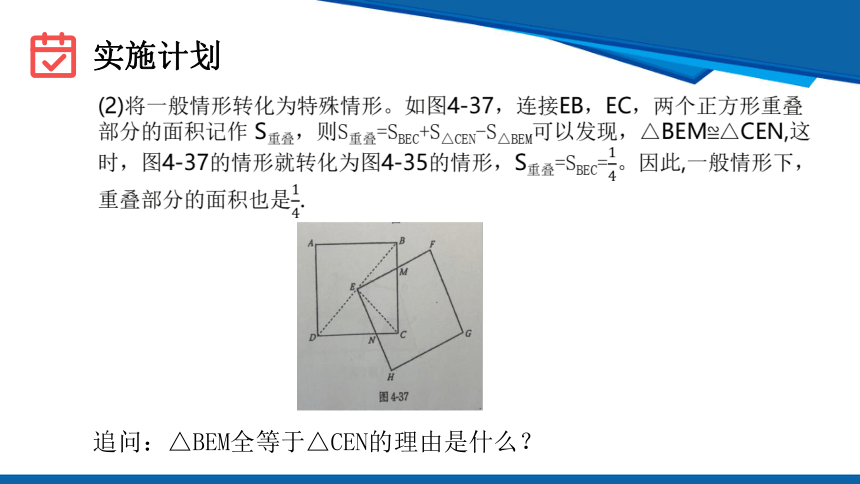
(2)将一般情形转化为特殊情形。如图4-37,连接EB,EC,两个正方形重叠部分的面积记作 S重叠,则S重叠=SBEC+S△CEN-S△BEM可以发现,△BEM≌△CEN,这时,图4-37的情形就转化为图4-35的情形,S重叠=SBEC=。因此,一般情形下,重叠部分的面积也是.
实施计划
追问:△BEM全等于△CEN的理由是什么?
回顾反思
(1)回顾本题的解决过程,你有哪些感悟
(2)具有什么特点的问题,可以从特殊情形入手 如何寻找特殊情形 与同伴进行交流。
C
即时测评
-ab
-a3b3
<
=
<
当堂达标
叁
当堂达标
叁
B
28
3.已知,在等边三角形ABC中,AD为BC边上的高.操作发现
(1)如图1,过点D分别作DE⊥AB,DF⊥AC,垂足分别为E,F.请直接写出DE+DF和AD的数量关系;
(2)如图2,若点P为AD上任意一点(不与A,D重合),过点P作PE⊥AB,PF⊥AC,垂足分别为E,F.判断PD+PE+PF和AD的数量关系,并说明理由;
拓广探索
(3)如图3,点P为等边三角形ABC内任意一点,过点P作PH⊥BC,PE⊥AB,PF⊥AC,垂足分别为H,E,F,探究PH+PE+PF和AD的数量关系,并说明理由。
(1)如图1,过点D分别作DE⊥AB,DF⊥AC,垂足分别为E,F.
请直接写出DE+DF和AD的数量关系;
因为
所以
所以
(2)如图2,若点P为AD上任意一点(不与A,D重合),过点P作PE⊥AB,PF⊥AC,垂足分别为E,F.判断PD+PE+PF和AD的数量关系,并说明理由;
解:PD+PE+PF=AD
理由如下:因为△ABC为等边三角形,
所以∠BAC=60°,
因为AD为BC边上的高,
所以∠BAD=∠CAD=
因为PE⊥AB,PF⊥AC,
所以PE=AP,PE=AP
所以PD+PE+PF=PD+AP=AD
(3)如图3,点P为等边三角形ABC内任意一点,过点P作PH⊥BC,PE⊥AB,PF⊥AC,垂足分别为H,E,F,
探究PH+PE+PF和AD的数量关系,并说明理由。
因为
所以
因为
所以
因为
所以
所以
所以
课堂小结
肆
课堂小结
肆
在利用特殊化法解决问题时,从特殊情形入手,借助特殊情形的经验解决一般情形下的问题,它的思考步骤为:
①不确定的是什么?
②有哪些限制条件?
③需要求的确定的是什么?
④下结论
常见的一些定值、定点等问题,均可用特殊值法求出答案!
课后作业
基础题:1.课后习题第 1,2题。
提高题:2.请学有余力的同学完成课后习题第3,4题
谢
谢
问题解决策略:特殊化
情境导入
壹
目
录
课堂小结
肆
当堂达标
叁
新知初探
贰
情境导入
壹
已知甲校学生数是乙校学生数的百分之四十,甲校女生数是甲校学生数的百分之三十,乙校男生数是乙校学生数的百分之四十二,那么两校女生总数占两校学生总数的百分之几
面对一般性问题时,可以先考虑特殊情形,借助特殊情形
下获得的结论或方法解决一般性问题,这就是特殊化策略。
一般性问题
一般性问题解决
特殊化
特殊问题
推广到
新知初探
贰
讲授新知
探究一:问题解决策略-特殊化
贰
问题:如图,有两个边长为1的正方形,其中正方形EFGH的顶点 E与正方形ABCD的中心重合。在正方形 EFGH绕点E旋转的过程中,两个正方形重叠部分的面积是多少
理解问题
(1)在旋转的过程中,两个正方形的重叠部分会呈现出哪些情形
(2)对于这些不同的情形,如何求两个正方形重叠部分的面积?你遇到的困难是什么?
拟定计划
(1)哪些特殊情形下,两个正方形重叠部分的面积容易求出?
(2)其他情形能转化为容易求解的特殊情形吗?
实施计划
(1) 先考虑特殊情形。如图4 -35、图4-36,这两种情形下,重叠部分的面积容易求出,都是
(2)将一般情形转化为特殊情形。如图4-37,连接EB,EC,两个正方形重叠部分的面积记作 S重叠,则S重叠=SBEC+S△CEN-S△BEM可以发现,△BEM≌△CEN,这时,图4-37的情形就转化为图4-35的情形,S重叠=SBEC=。因此,一般情形下,重叠部分的面积也是.
实施计划
追问:△BEM全等于△CEN的理由是什么?
回顾反思
(1)回顾本题的解决过程,你有哪些感悟
(2)具有什么特点的问题,可以从特殊情形入手 如何寻找特殊情形 与同伴进行交流。
C
即时测评
-ab
-a3b3
<
=
<
当堂达标
叁
当堂达标
叁
B
28
3.已知,在等边三角形ABC中,AD为BC边上的高.操作发现
(1)如图1,过点D分别作DE⊥AB,DF⊥AC,垂足分别为E,F.请直接写出DE+DF和AD的数量关系;
(2)如图2,若点P为AD上任意一点(不与A,D重合),过点P作PE⊥AB,PF⊥AC,垂足分别为E,F.判断PD+PE+PF和AD的数量关系,并说明理由;
拓广探索
(3)如图3,点P为等边三角形ABC内任意一点,过点P作PH⊥BC,PE⊥AB,PF⊥AC,垂足分别为H,E,F,探究PH+PE+PF和AD的数量关系,并说明理由。
(1)如图1,过点D分别作DE⊥AB,DF⊥AC,垂足分别为E,F.
请直接写出DE+DF和AD的数量关系;
因为
所以
所以
(2)如图2,若点P为AD上任意一点(不与A,D重合),过点P作PE⊥AB,PF⊥AC,垂足分别为E,F.判断PD+PE+PF和AD的数量关系,并说明理由;
解:PD+PE+PF=AD
理由如下:因为△ABC为等边三角形,
所以∠BAC=60°,
因为AD为BC边上的高,
所以∠BAD=∠CAD=
因为PE⊥AB,PF⊥AC,
所以PE=AP,PE=AP
所以PD+PE+PF=PD+AP=AD
(3)如图3,点P为等边三角形ABC内任意一点,过点P作PH⊥BC,PE⊥AB,PF⊥AC,垂足分别为H,E,F,
探究PH+PE+PF和AD的数量关系,并说明理由。
因为
所以
因为
所以
因为
所以
所以
所以
课堂小结
肆
课堂小结
肆
在利用特殊化法解决问题时,从特殊情形入手,借助特殊情形的经验解决一般情形下的问题,它的思考步骤为:
①不确定的是什么?
②有哪些限制条件?
③需要求的确定的是什么?
④下结论
常见的一些定值、定点等问题,均可用特殊值法求出答案!
课后作业
基础题:1.课后习题第 1,2题。
提高题:2.请学有余力的同学完成课后习题第3,4题
谢
谢
