辽宁省朝阳市建平县实验中学2024-2025学年高二下学期7月月考数学试题(PDF版、含答案)
文档属性
| 名称 | 辽宁省朝阳市建平县实验中学2024-2025学年高二下学期7月月考数学试题(PDF版、含答案) |

|
|
| 格式 | |||
| 文件大小 | 254.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 12:24:15 | ||
图片预览


文档简介
辽宁省朝阳市建平县实验中学 2024-2025学年高二下学期
7月月考数学试题
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.已知 i 为虚数单位,复数 (1 3i)z 3 4i,则 | z | ( )
A.1 B. 2 10C. D. 10
2
2.数学老师从 6 道习题中随机抽 3 道让同学检测,规定至少要解答正确 2 道题才能及格.某同学只能求解其
中的 4 道题,则他能及格的概率是( )
1 2 3 4
A. B. C. D.
5 5 5 5
3.现将 A,B,C,D,E,F六名学生排成一排,要求 D,E相邻,且 C,F不相邻,则不同的排列方式有( )
A.144 种 B.240 种 C.120 种 D.72 种
4.已知等差数列 an 的前 n项和为 Sn,若 S3 9,S9 3,则 S16 ( )
400 134 136
A. B.-44 C. D.
9 3 3
5 直三棱柱 ABC A1B1C1 中, AB AC AA1, AB AC,则 AB1 与 BC所成的角的大小为( )
A 30 B. 45 C. 60 D. 90
6.点 P是曲线 y x2 lnx上任意一点,则点 P到直线 y=x-4 的距离的最小值是( )
A.1 B. 2 C.2 D. 2 2
7.已知直线 l : 3x 4y 16 0,点 P为圆C : (x 2)2 y 2 1上一动点,则点 P到直线 l的最小距离为
( )
A.1 B.2 C.3 D.4
8.已知 a 0 x,不等式 xe ax a ln x恒成立,则实数 a的取值范围为( )
1
A.[1,e] B. 0,
c. (0,e]
1
D.
e
,1
e
二、选择题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
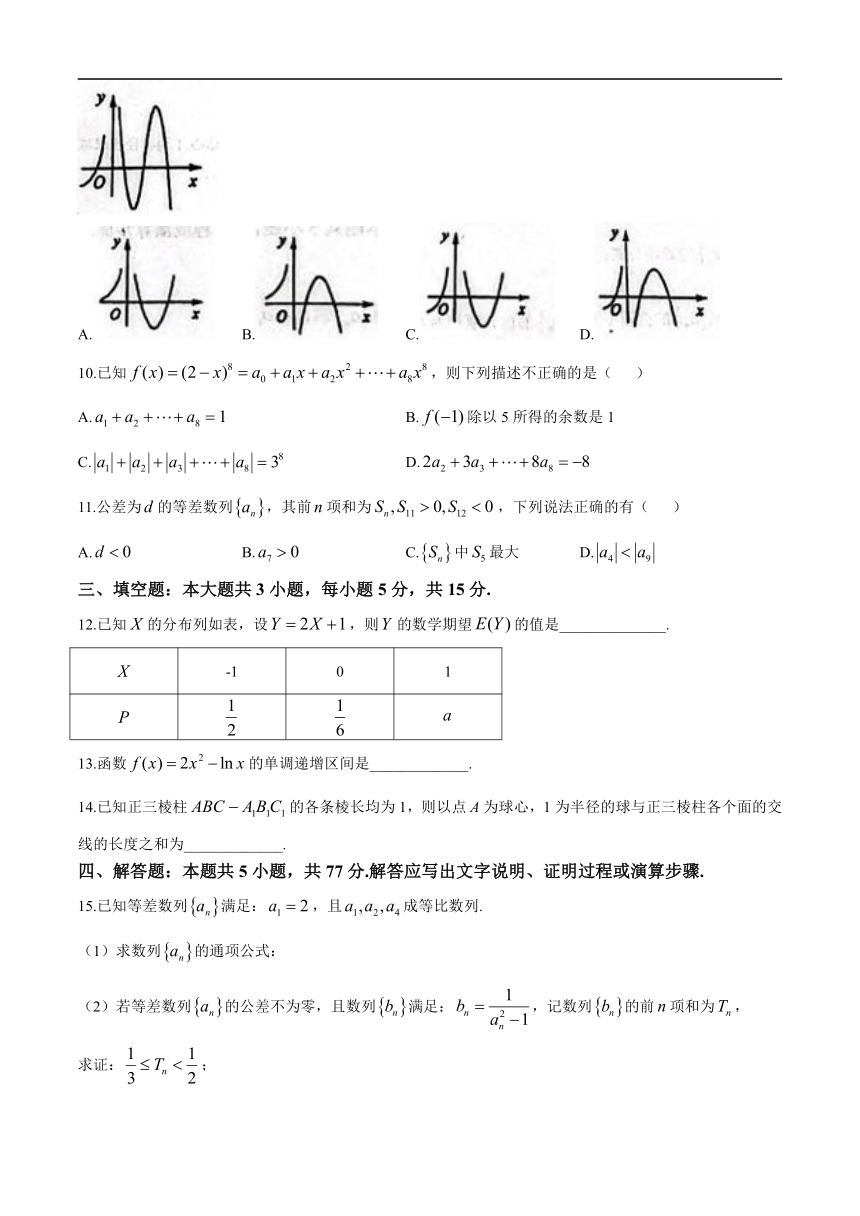
9.设函数 f (x)在定义域内可导, y f (x) 的图象如图所示,则导函数 y f (x) 的图象不可能是( )
A. B. C. D.
10.已知 f (x) (2 x)8 a0 a1x a2x
2 a8x
8
,则下列描述不正确的是( )
A.a1 a2 a8 1 B. f ( 1) 除以 5 所得的余数是 1
C. a1 a2 a3 a 3
8
8 D. 2a2 3a3 8a8 8
11.公差为d 的等差数列 an ,其前n项和为 Sn ,S11 0,S12 0 ,下列说法正确的有( )
A.d 0 B.a7 0 C. Sn 中 S5 最大 D. a4 a9
三、填空题:本大题共 3小题,每小题 5分,共 15分.
12.已知 X 的分布列如表,设Y 2X 1,则Y 的数学期望E(Y ) 的值是______________.
X -1 0 1
1 1
P a
2 6
13. 2函数 f (x) 2x ln x的单调递增区间是_____________.
14.已知正三棱柱 ABC A1B1C1 的各条棱长均为 1,则以点 A为球心,1 为半径的球与正三棱柱各个面的交
线的长度之和为_____________.
四、解答题:本题共 5小题,共 77分.解答应写出文字说明、证明过程或演算步骤.
15.已知等差数列 an 满足:a1 2 ,且 a1,a2 ,a4 成等比数列.
(1)求数列 an 的通项公式:
(2)若等差数列 an 的公差不为零,且数列 bn
1
满足:bn 2 ,记数列 bn 的前 n项和为T ,a nn 1
1 T 1求证: ;
3 n 2
16.如图,在直三棱柱 ABC A1B1C1 中, ACB为直角,侧面 ACC1A1 为正方形, AC BC 2 ,D,E
分别为 AB,AC1 的中点.
(1)求证:DE / / 平面 BB1C1C;
(2)求证: AC DE ;
(3)求直线 AC1 与平面 B1DE所成角的正弦值.
B C
17 在 ABC 中,角 A,B,C 的对边分别是a,b,c,bsin a sinB,BC 3,如图所示,点D在线段 AC
2
上,满足 AB AD .
(1)求 A的值;
(2)若 BD 2CD,求 AB CB的值.
18.目前电动车的电池有石墨烯电池与铅酸电池两种,某公司为了了解该市电动车消费者对这两种电池电动
车的偏好,随机调查了 500 名电动车用户,其中男性用户 300 名,在被调查的女性用户中偏好铅酸电池电
3
动车的占 ,得到以下的2 2列联表:
5
偏好石墨烯电池电动车 偏好铅酸电池电动车 合计
男性用户 200 300
女性用户
合计 500
(1)根据以上数据,完成2 2列联表,依据小概率值 0.005的独立性检验,能否认为该市电动车用户
对这两种电池的电动东的偏好与性别有关;
(2)从偏好石墨烯电池电动车的用户中按性别比例用分层随机抽样的方法随机抽取 7 人进行问卷调查,再
从这 7 名用户中抽取 2 人进行座谈,在有女性用户参加座谈的条件下,求恰有两名女性用户参加座谈的概
率;
(3)用样本的频率估计概率,在该市所有女性电动车用户中随机抽取 3 名进行新车试驾,记 3 名参加试驾
的女性用户中偏好石墨烯电池电动车的人数为 X ,求 X 的分布列.
2 n(ad bc)2
参考公式: ,其中 n a b c d .
(a b)(c d )(a c)(b d )
参考数据:
0.100 0.050 0.025 0.010 0.005 0.001
x 2.706 3.841 5.024 6.635 7.879 10.828
19.已知点F1,F
2 2
2 分别是双曲线C1 : x y 2的左右焦点,过 F2 的直线交双曲线右支于 P,A两点,点 P在
第一象限.
(1)求点 P横坐标的取值范围;
(2)线段 PF1交圆C2 : (x 2)
2 y2 8于点 B,记 PF2B, AF2F1, PAF1 的面积分别为 S1,S2 ,S,求
S S
的最小值.
S1 S2
建平县实验中学 2024-2025年高二月考数学试卷
一:单选题答案
1.C 2.D 3.A 4.A 5.C 6.D 7.A 8.A
8 题【答案】C
【解析】
x
【分析】设 f (x) xe a(x ln x) 由题可知 f (x)min 0,利用导函数研究 f (x) 单调性知存在 x0 使得
f x0 0 x,此时得a x 00e ,而 f (x)min f x0 0 ,即1 x0 ln x0 0 ,则即 x0 ln x0 1构造
g(x) x ln x,由 g(x)的单调性可知, x0 (0,1],构造 h(x) xe
x , x (0,1],利用导函数研究 h(x) 的
单调性,进而求得 h(x) 的值域,得出 a的取值范围.
x
【详解】解法一:不等式 xe ax a ln x x,即 xe a(x ln x) 0 ,
设 f (x) xe x a(x ln x) ,则 f (x) (x 1)e x a 1
1
(1 x)
e x a
x x
, x 0 ,
x
令 f x0 0,则a x0e 0 ,
当 x 0, x0 时, f (x) 0, f (x) 单调递减,
当 x x , f 0 时, (x) 0, f (x) 单调递增.
故只需 f (x) x0 x0min f x0 x0e a x0 ln x0 x0e 1 x0 ln x0 0,
所以1 x0 ln x0 0 ,即 x0 ln x0 1 .
设 g(x) x ln x,则 g(x)在 (0, ) 上单调递增,又 g(1) 1,
所以 x0 (0,1],设 h(x) xe
x , x (0,1] x,则 h (x) (1 x)e 0 ,
所以 h(x) 在 (0,1]上单调递增,所以 h(x) 的值域为 (0,e],即 a的取值范围为 (0,e] .
解法二:由题意将原不等式变形可得 a(x ln x) xe x a(x ln x) e lnxe x ,
a(x ln x) t即 e x ln x x ln x t R at et,令 ,则有 ,即a t 1e
因为 a 0 t 1,所以有 t 对于任意的 t R 恒成立,e a
f (t) t 1 t令 t ,则 f (t) e et
因为 f (1) 0 ,且当 t ( ,1) 时, f (t) 0, f (t) 单调逆增;当 t (1, )时, f (t) 0, f (t) 单调递减;
所以 f (t) 在 x 1处取极大值,也是 f (t) 的最大值
1
所以 f (t) 1
a max
f (1)
e
又因为a 0,所以a (0,e]
故选:C
二题多选题答案
9.【答案】ACD
10.【答案】ACD
11.AD
三、填空题:本大题共 3小题,每小题 5分,共 15分.
2
12.故答案为: .
3
1 1
【详解】由已知得 a 1
2 6
a 1 ,
3
E(X ) 1 1 1 ,
2 3 6
QE(Y ) 2E(X ) 1,
E(Y ) 2 .
3
1
13. , 【答案】
2
3π
14.【答案】
2
四、解答题:本题共 5小题,共 77分.解答应写出文字说明、证明过程或演算步骤.
15.答案:【小问 1 详解】设数列 an 的公差为d ,依题意:2,2 d ,2 3d 成等比数列,
所以 (2 d )2 2(2 3d ) ,解得: d 0或d 2
当d 0时,an 2 ,当d 2时,an 2 (n 1) 2 2n
所以数列 an 的通项公式为 an 2 或an 2n
【小问 2 详解】
*
因为等差数列 an 的公差不为零,由(1)知an 2n n N
b 1 1 1 1 1则 n
an 1 an 1 (2n 1)(2n 1) 2 2n 1 2n 1
T 1 所以 n 1
1 1 1 1 1 1 1 1 1 1
1 ,故T 1 2 3 3 5 2n 1 2n 1 2 2n 1 n 2 2n 1
2
T 1 1 1 1 1 1而 n 随 n的增大而增大,则Tn T1 ,故 Tn 成立2 2n 1 3 3 2
16 题答案【小问 1 详解】
连接 BC1,因为 D,E分别为 AB,AC1 的中点,
所以DE / /BC1 ,
因为 BC1 平面 BB1C1C ,DE 平面 BB1C1C,
所以DE / / 平面 BB1C1C;
【小问 2 详解】直三棱柱 ABC A1B1C1 中, ACB为直角,
故 AC BC,AC CC1,
又BC,CC1 平面 BCC1B1,BC CC1 C ,
所以 AC 平面 BCC1B1,
又BC1 平面 BCC1B1,所以 AC BC1 ,
由(1)知,DE / /BC1 ,
所以 AC DE ;
【小问 3 详解】
以C为坐标原点,CA,CB,CC1所在直线分别为 x,y,z轴,建立空间直角坐标系,
侧面 ACC1A1 为正方形, AC BC 2 ,
故 A(2,0,0),C1(0,0,2),B1(0,2,2),D(1,1,0),E(1,0,1) ,
设平面B1DE
的法向量为m (x, y, z),
m B1D (x, y, z) (1, 1, 2) x y 2z 0
则 ,
m B1E (x, y, z) (1, 2, 1) x 2y z 0
令 z 1得 x 3, y 1,故m (3,1,1),
设直线 AC1 与平面 B1DE所成角的大小为 ,
AC1 msin cos AC ,m | ( 2,0,2) (3,1,1) | 22则 1 .
AC 1 |m | 4 4 9 1 1 11
B C
17 题:【详解】(1)由正弦定理得: sinBsin sin AsinB,
2
B C π A, sin B C sin π A A cos ,2 2 2 2
又B (0,π), sinB 0, A A cos sin A 2sin cos A,
2 2 2
A 0,
π
, cos
A
0, sin A 1 ,
2 2 2 2 2
A π π
,解得: A .
2 6 3
AB AD,A π(2) , ABD 为等边三角形,
3
设DC x,则 BD AB AD 2x,
在 ABC 中,由余弦定理得:
BC2 AB2 AC2 2AB AC cos A 4x2 9x2 6x2 3 7 9 ,解得: x
7
AB 6 7 , AC 9 7
2 2 2
, cosB AB BC AC 7 ,
7 7 2AB BC 14
6 7 7 9
AB CB | AB | | BC | cosB 3 .
7 14 7
18 题:【小问 1 详解】
被调查的女性市民人数为500 200 100 200,
其中偏好铅酸电池电动车的女性市民人数为200 3 120 .
5
偏好石墨烯电池电动车的女性市民人数为 200 120 80,
所以2 2列联表为:
偏好石墨烯电池电动车 偏好铅酸电池电动车 合计
男性市民 200 100 300
女性市民 80 120 200
合计 280 220 500
零假设H0 :市民对这两种电池的电动车的偏好与市民的性别无关,
根据列联表中的数据可以求得
2 n(ad bc)
2 500 (200 120 80 100)2
34.632 ,
(a b)(c d )(a c)(b d ) 300 200 280 220
2由于 34.632 7.879 ,
根据小概率值 0.005的独立性检验,我们推断H0 不成立,
即认为市民对这两种电池的电动车的偏好与市民的性别有关.
【小问 2 详解】
200 5
因为偏好石墨烯电池电动车的市民中,男性市民与女性市民的比为 ,
80 2
所以采用分层抽样的方法抽取 7 的人中,男性市民有 5 人,女性市民有 2 人,
设“有女性市民参加座谈”为事件 A,“恰有两名女性市民参加座谈”为事件 B,
C2 1 C1C1 2
则P(AB) 22 ,P(A)
5 2 C2 11
C 21 C2
,
7 7 21
1
所以 P(B∣A) P(AB) 21 1
P(A) 11 11
21
【小问 3 详解】
80 2
根据频率估计概率知,女性用户中偏好石墨烯电池电动车的概率为 ,
200 5
120 3
偏好铅酸电池电动车的概率为 ,
200 5
参加试驾的女性用户中偏好石墨烯电池电动车的人数为 X,X可能取值为 0,1,2,3,
2 0P(X 0) C0 3
3
27 3 5
,
5 125
1 2
P(X 1) C1 2 3 54 3 5 5
,
125
2 1
P(X 2) C2 2 3 363 ,
5 5 125
3 0
P(X 3) C3 2 3 83 ,
5 5 125
故 X 的分布列如下:
X 0 1 2 3
27 54 36 8
P
125 125 125 125
22
证明过程见解析(3)
11
19 题答案
x2 y2
【小问 1 2 2详解】由双曲线C1 : x y 2即 1可得交点 F2 (2,0) ,2 2
设P x1, y1 ,A x2 , y2 ,PF2 F2A ,则 0,
2 x1 x
2
1
根据向量定比分点公式: ,
0 y y 1 2
1
x2 y2 2 x2 y2
P,A 1 1 1 1
2
将 坐标代入双曲线得: 2 ,
x2 y
2
2 2
2 2 2
x2 y
2 2
2 2
两式相减得: x1 x2 x1 x2 2 1 2 x1 x2 2(1 ) 2(1 )(1 )
则有: x1 x2 1 ,再结合 x1 x2 2(1 ) x
3 3
,解得 1 ,2 2 2
3
故 x1 ,
.
2
x2 y2 2
【小问 2 详解】由 1可得 e 2 ,
2 2 2
2 2 2
P x x y b1, y1 在 1 y2 x2 b2上则有2 2 1 a2 1
2
PF1 x1 c
2 y21 , 将 y
2 b 2
1 2 x1 b
2
代入,
a
2 2
PF x c 2 b x 2 b 2 x 2 2cx c 2 b x 2 b 21 1 a2 1 1 1 a2 1
b2
1
2
2 x1 2x1 a
2 e2x21 2x1 a
2 x1 a
2 x a,
a
1
根据双曲线的定义 PF1 PF2 2a, PF2 ex1 a,
显然 | PB | PF1 2 2 PF2 ,
S PF1 |PA | PF1 |PA | ex1 a 1
S1 |PB | PF2 PF2 PF2 ex1 a
2 3 2
2 2 1 5 1 5 ,
2 3 2 1 2 2
S | PA |
1 ,
S2 AF2
S S 5 5则 1 2 2 5 2,当且仅当 5 时取等号,
S1 S2
S S
故 为 2 5 2 .
S1 S2
7月月考数学试题
一、选择题:本题共 8小题,每小题 5分,共 40分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.已知 i 为虚数单位,复数 (1 3i)z 3 4i,则 | z | ( )
A.1 B. 2 10C. D. 10
2
2.数学老师从 6 道习题中随机抽 3 道让同学检测,规定至少要解答正确 2 道题才能及格.某同学只能求解其
中的 4 道题,则他能及格的概率是( )
1 2 3 4
A. B. C. D.
5 5 5 5
3.现将 A,B,C,D,E,F六名学生排成一排,要求 D,E相邻,且 C,F不相邻,则不同的排列方式有( )
A.144 种 B.240 种 C.120 种 D.72 种
4.已知等差数列 an 的前 n项和为 Sn,若 S3 9,S9 3,则 S16 ( )
400 134 136
A. B.-44 C. D.
9 3 3
5 直三棱柱 ABC A1B1C1 中, AB AC AA1, AB AC,则 AB1 与 BC所成的角的大小为( )
A 30 B. 45 C. 60 D. 90
6.点 P是曲线 y x2 lnx上任意一点,则点 P到直线 y=x-4 的距离的最小值是( )
A.1 B. 2 C.2 D. 2 2
7.已知直线 l : 3x 4y 16 0,点 P为圆C : (x 2)2 y 2 1上一动点,则点 P到直线 l的最小距离为
( )
A.1 B.2 C.3 D.4
8.已知 a 0 x,不等式 xe ax a ln x恒成立,则实数 a的取值范围为( )
1
A.[1,e] B. 0,
c. (0,e]
1
D.
e
,1
e
二、选择题:本题共 3小题,每小题 6分,共 18分.在每小题给出的选项中,有多项符合题目
要求.全部选对的得 6分,部分选对的得部分分,有选错的得 0分.
9.设函数 f (x)在定义域内可导, y f (x) 的图象如图所示,则导函数 y f (x) 的图象不可能是( )
A. B. C. D.
10.已知 f (x) (2 x)8 a0 a1x a2x
2 a8x
8
,则下列描述不正确的是( )
A.a1 a2 a8 1 B. f ( 1) 除以 5 所得的余数是 1
C. a1 a2 a3 a 3
8
8 D. 2a2 3a3 8a8 8
11.公差为d 的等差数列 an ,其前n项和为 Sn ,S11 0,S12 0 ,下列说法正确的有( )
A.d 0 B.a7 0 C. Sn 中 S5 最大 D. a4 a9
三、填空题:本大题共 3小题,每小题 5分,共 15分.
12.已知 X 的分布列如表,设Y 2X 1,则Y 的数学期望E(Y ) 的值是______________.
X -1 0 1
1 1
P a
2 6
13. 2函数 f (x) 2x ln x的单调递增区间是_____________.
14.已知正三棱柱 ABC A1B1C1 的各条棱长均为 1,则以点 A为球心,1 为半径的球与正三棱柱各个面的交
线的长度之和为_____________.
四、解答题:本题共 5小题,共 77分.解答应写出文字说明、证明过程或演算步骤.
15.已知等差数列 an 满足:a1 2 ,且 a1,a2 ,a4 成等比数列.
(1)求数列 an 的通项公式:
(2)若等差数列 an 的公差不为零,且数列 bn
1
满足:bn 2 ,记数列 bn 的前 n项和为T ,a nn 1
1 T 1求证: ;
3 n 2
16.如图,在直三棱柱 ABC A1B1C1 中, ACB为直角,侧面 ACC1A1 为正方形, AC BC 2 ,D,E
分别为 AB,AC1 的中点.
(1)求证:DE / / 平面 BB1C1C;
(2)求证: AC DE ;
(3)求直线 AC1 与平面 B1DE所成角的正弦值.
B C
17 在 ABC 中,角 A,B,C 的对边分别是a,b,c,bsin a sinB,BC 3,如图所示,点D在线段 AC
2
上,满足 AB AD .
(1)求 A的值;
(2)若 BD 2CD,求 AB CB的值.
18.目前电动车的电池有石墨烯电池与铅酸电池两种,某公司为了了解该市电动车消费者对这两种电池电动
车的偏好,随机调查了 500 名电动车用户,其中男性用户 300 名,在被调查的女性用户中偏好铅酸电池电
3
动车的占 ,得到以下的2 2列联表:
5
偏好石墨烯电池电动车 偏好铅酸电池电动车 合计
男性用户 200 300
女性用户
合计 500
(1)根据以上数据,完成2 2列联表,依据小概率值 0.005的独立性检验,能否认为该市电动车用户
对这两种电池的电动东的偏好与性别有关;
(2)从偏好石墨烯电池电动车的用户中按性别比例用分层随机抽样的方法随机抽取 7 人进行问卷调查,再
从这 7 名用户中抽取 2 人进行座谈,在有女性用户参加座谈的条件下,求恰有两名女性用户参加座谈的概
率;
(3)用样本的频率估计概率,在该市所有女性电动车用户中随机抽取 3 名进行新车试驾,记 3 名参加试驾
的女性用户中偏好石墨烯电池电动车的人数为 X ,求 X 的分布列.
2 n(ad bc)2
参考公式: ,其中 n a b c d .
(a b)(c d )(a c)(b d )
参考数据:
0.100 0.050 0.025 0.010 0.005 0.001
x 2.706 3.841 5.024 6.635 7.879 10.828
19.已知点F1,F
2 2
2 分别是双曲线C1 : x y 2的左右焦点,过 F2 的直线交双曲线右支于 P,A两点,点 P在
第一象限.
(1)求点 P横坐标的取值范围;
(2)线段 PF1交圆C2 : (x 2)
2 y2 8于点 B,记 PF2B, AF2F1, PAF1 的面积分别为 S1,S2 ,S,求
S S
的最小值.
S1 S2
建平县实验中学 2024-2025年高二月考数学试卷
一:单选题答案
1.C 2.D 3.A 4.A 5.C 6.D 7.A 8.A
8 题【答案】C
【解析】
x
【分析】设 f (x) xe a(x ln x) 由题可知 f (x)min 0,利用导函数研究 f (x) 单调性知存在 x0 使得
f x0 0 x,此时得a x 00e ,而 f (x)min f x0 0 ,即1 x0 ln x0 0 ,则即 x0 ln x0 1构造
g(x) x ln x,由 g(x)的单调性可知, x0 (0,1],构造 h(x) xe
x , x (0,1],利用导函数研究 h(x) 的
单调性,进而求得 h(x) 的值域,得出 a的取值范围.
x
【详解】解法一:不等式 xe ax a ln x x,即 xe a(x ln x) 0 ,
设 f (x) xe x a(x ln x) ,则 f (x) (x 1)e x a 1
1
(1 x)
e x a
x x
, x 0 ,
x
令 f x0 0,则a x0e 0 ,
当 x 0, x0 时, f (x) 0, f (x) 单调递减,
当 x x , f 0 时, (x) 0, f (x) 单调递增.
故只需 f (x) x0 x0min f x0 x0e a x0 ln x0 x0e 1 x0 ln x0 0,
所以1 x0 ln x0 0 ,即 x0 ln x0 1 .
设 g(x) x ln x,则 g(x)在 (0, ) 上单调递增,又 g(1) 1,
所以 x0 (0,1],设 h(x) xe
x , x (0,1] x,则 h (x) (1 x)e 0 ,
所以 h(x) 在 (0,1]上单调递增,所以 h(x) 的值域为 (0,e],即 a的取值范围为 (0,e] .
解法二:由题意将原不等式变形可得 a(x ln x) xe x a(x ln x) e lnxe x ,
a(x ln x) t即 e x ln x x ln x t R at et,令 ,则有 ,即a t 1e
因为 a 0 t 1,所以有 t 对于任意的 t R 恒成立,e a
f (t) t 1 t令 t ,则 f (t) e et
因为 f (1) 0 ,且当 t ( ,1) 时, f (t) 0, f (t) 单调逆增;当 t (1, )时, f (t) 0, f (t) 单调递减;
所以 f (t) 在 x 1处取极大值,也是 f (t) 的最大值
1
所以 f (t) 1
a max
f (1)
e
又因为a 0,所以a (0,e]
故选:C
二题多选题答案
9.【答案】ACD
10.【答案】ACD
11.AD
三、填空题:本大题共 3小题,每小题 5分,共 15分.
2
12.故答案为: .
3
1 1
【详解】由已知得 a 1
2 6
a 1 ,
3
E(X ) 1 1 1 ,
2 3 6
QE(Y ) 2E(X ) 1,
E(Y ) 2 .
3
1
13. , 【答案】
2
3π
14.【答案】
2
四、解答题:本题共 5小题,共 77分.解答应写出文字说明、证明过程或演算步骤.
15.答案:【小问 1 详解】设数列 an 的公差为d ,依题意:2,2 d ,2 3d 成等比数列,
所以 (2 d )2 2(2 3d ) ,解得: d 0或d 2
当d 0时,an 2 ,当d 2时,an 2 (n 1) 2 2n
所以数列 an 的通项公式为 an 2 或an 2n
【小问 2 详解】
*
因为等差数列 an 的公差不为零,由(1)知an 2n n N
b 1 1 1 1 1则 n
an 1 an 1 (2n 1)(2n 1) 2 2n 1 2n 1
T 1 所以 n 1
1 1 1 1 1 1 1 1 1 1
1 ,故T 1 2 3 3 5 2n 1 2n 1 2 2n 1 n 2 2n 1
2
T 1 1 1 1 1 1而 n 随 n的增大而增大,则Tn T1 ,故 Tn 成立2 2n 1 3 3 2
16 题答案【小问 1 详解】
连接 BC1,因为 D,E分别为 AB,AC1 的中点,
所以DE / /BC1 ,
因为 BC1 平面 BB1C1C ,DE 平面 BB1C1C,
所以DE / / 平面 BB1C1C;
【小问 2 详解】直三棱柱 ABC A1B1C1 中, ACB为直角,
故 AC BC,AC CC1,
又BC,CC1 平面 BCC1B1,BC CC1 C ,
所以 AC 平面 BCC1B1,
又BC1 平面 BCC1B1,所以 AC BC1 ,
由(1)知,DE / /BC1 ,
所以 AC DE ;
【小问 3 详解】
以C为坐标原点,CA,CB,CC1所在直线分别为 x,y,z轴,建立空间直角坐标系,
侧面 ACC1A1 为正方形, AC BC 2 ,
故 A(2,0,0),C1(0,0,2),B1(0,2,2),D(1,1,0),E(1,0,1) ,
设平面B1DE
的法向量为m (x, y, z),
m B1D (x, y, z) (1, 1, 2) x y 2z 0
则 ,
m B1E (x, y, z) (1, 2, 1) x 2y z 0
令 z 1得 x 3, y 1,故m (3,1,1),
设直线 AC1 与平面 B1DE所成角的大小为 ,
AC1 msin cos AC ,m | ( 2,0,2) (3,1,1) | 22则 1 .
AC 1 |m | 4 4 9 1 1 11
B C
17 题:【详解】(1)由正弦定理得: sinBsin sin AsinB,
2
B C π A, sin B C sin π A A cos ,2 2 2 2
又B (0,π), sinB 0, A A cos sin A 2sin cos A,
2 2 2
A 0,
π
, cos
A
0, sin A 1 ,
2 2 2 2 2
A π π
,解得: A .
2 6 3
AB AD,A π(2) , ABD 为等边三角形,
3
设DC x,则 BD AB AD 2x,
在 ABC 中,由余弦定理得:
BC2 AB2 AC2 2AB AC cos A 4x2 9x2 6x2 3 7 9 ,解得: x
7
AB 6 7 , AC 9 7
2 2 2
, cosB AB BC AC 7 ,
7 7 2AB BC 14
6 7 7 9
AB CB | AB | | BC | cosB 3 .
7 14 7
18 题:【小问 1 详解】
被调查的女性市民人数为500 200 100 200,
其中偏好铅酸电池电动车的女性市民人数为200 3 120 .
5
偏好石墨烯电池电动车的女性市民人数为 200 120 80,
所以2 2列联表为:
偏好石墨烯电池电动车 偏好铅酸电池电动车 合计
男性市民 200 100 300
女性市民 80 120 200
合计 280 220 500
零假设H0 :市民对这两种电池的电动车的偏好与市民的性别无关,
根据列联表中的数据可以求得
2 n(ad bc)
2 500 (200 120 80 100)2
34.632 ,
(a b)(c d )(a c)(b d ) 300 200 280 220
2由于 34.632 7.879 ,
根据小概率值 0.005的独立性检验,我们推断H0 不成立,
即认为市民对这两种电池的电动车的偏好与市民的性别有关.
【小问 2 详解】
200 5
因为偏好石墨烯电池电动车的市民中,男性市民与女性市民的比为 ,
80 2
所以采用分层抽样的方法抽取 7 的人中,男性市民有 5 人,女性市民有 2 人,
设“有女性市民参加座谈”为事件 A,“恰有两名女性市民参加座谈”为事件 B,
C2 1 C1C1 2
则P(AB) 22 ,P(A)
5 2 C2 11
C 21 C2
,
7 7 21
1
所以 P(B∣A) P(AB) 21 1
P(A) 11 11
21
【小问 3 详解】
80 2
根据频率估计概率知,女性用户中偏好石墨烯电池电动车的概率为 ,
200 5
120 3
偏好铅酸电池电动车的概率为 ,
200 5
参加试驾的女性用户中偏好石墨烯电池电动车的人数为 X,X可能取值为 0,1,2,3,
2 0P(X 0) C0 3
3
27 3 5
,
5 125
1 2
P(X 1) C1 2 3 54 3 5 5
,
125
2 1
P(X 2) C2 2 3 363 ,
5 5 125
3 0
P(X 3) C3 2 3 83 ,
5 5 125
故 X 的分布列如下:
X 0 1 2 3
27 54 36 8
P
125 125 125 125
22
证明过程见解析(3)
11
19 题答案
x2 y2
【小问 1 2 2详解】由双曲线C1 : x y 2即 1可得交点 F2 (2,0) ,2 2
设P x1, y1 ,A x2 , y2 ,PF2 F2A ,则 0,
2 x1 x
2
1
根据向量定比分点公式: ,
0 y y 1 2
1
x2 y2 2 x2 y2
P,A 1 1 1 1
2
将 坐标代入双曲线得: 2 ,
x2 y
2
2 2
2 2 2
x2 y
2 2
2 2
两式相减得: x1 x2 x1 x2 2 1 2 x1 x2 2(1 ) 2(1 )(1 )
则有: x1 x2 1 ,再结合 x1 x2 2(1 ) x
3 3
,解得 1 ,2 2 2
3
故 x1 ,
.
2
x2 y2 2
【小问 2 详解】由 1可得 e 2 ,
2 2 2
2 2 2
P x x y b1, y1 在 1 y2 x2 b2上则有2 2 1 a2 1
2
PF1 x1 c
2 y21 , 将 y
2 b 2
1 2 x1 b
2
代入,
a
2 2
PF x c 2 b x 2 b 2 x 2 2cx c 2 b x 2 b 21 1 a2 1 1 1 a2 1
b2
1
2
2 x1 2x1 a
2 e2x21 2x1 a
2 x1 a
2 x a,
a
1
根据双曲线的定义 PF1 PF2 2a, PF2 ex1 a,
显然 | PB | PF1 2 2 PF2 ,
S PF1 |PA | PF1 |PA | ex1 a 1
S1 |PB | PF2 PF2 PF2 ex1 a
2 3 2
2 2 1 5 1 5 ,
2 3 2 1 2 2
S | PA |
1 ,
S2 AF2
S S 5 5则 1 2 2 5 2,当且仅当 5 时取等号,
S1 S2
S S
故 为 2 5 2 .
S1 S2
同课章节目录
