山东省东营市2024-2025学年(五四学制)七年级下学期7月期末考试数学试卷(含详解)
文档属性
| 名称 | 山东省东营市2024-2025学年(五四学制)七年级下学期7月期末考试数学试卷(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 13:21:10 | ||
图片预览



文档简介
山东省东营市2024-2025学年七年级下学期7月期末数学试题
一、单选题
1.下列方程组中是二元一次方程组的是( )
A. B. C. D.
2.已知,将含角的直角三角板如图放置,若,则的度数为( )
A. B. C. D.
3.若,则下列不等式正确的是( )
A. B.
C. D.
4.欧阳修在《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆其口,徐以构酌油之,自钱孔入,而钱不湿”,可见卖油的技艺之高超.如图,若铜钱半径为,中间有边长为的正方形小孔,随机向铜钱上滴一滴油(油滴大小忽略不计),则油恰好落入孔中的概率是( )
A. B. C. D.
5.5月26日,“2023中国国际大数据产业博览会”在贵阳开幕,在“自动化立体库”中有许多几何元素,其中有一个等腰三角形模型(示意图如图所示),它的顶角为,腰长为,则底边上的高是( )
A. B. C. D.
6.如图,若直线与直线交于一点,则关于的不等式的解集是( )
A. B. C. D.
7.我国古典数学文献《增删算法统宗·六均输》中有一个“隔沟计算”的问题:甲乙两人隔一条沟放牧,二人心里暗中合计,甲对乙说:“我得到你的九只羊,我的羊就比你多一倍.”乙对甲说:“我得到你的九只羊,咱俩家的羊一样多.”请问甲乙各有多少只羊呢?两个人在沟两边闲坐,心里很烦躁,因为在地上画了半晌,也没算出来.设甲有羊x只,乙有羊y只,则得合题意的方程组是( )
A. B.
C. D.
8.如图,在中,,,,以为圆心,适当长为半径画弧,分别交,于,两点,再分别以,为圆心,大于的长为半径画弧,两弧交于点.作射线交于点,则的面积是( )
A. B. C. D.
9.如图,,,,,垂足分别是点、,,,则的长是( )
A. B. C. D.
10.已知:如图,中,点是边上一点,,,平分,且于,与相交于点,若于,交于点.有以下结论:
①;②;③若连接,则;④点是的中点;⑤与成轴对称.以上五个结论中正确的是( )
A.①③⑤ B.①④⑤ C.①②③⑤ D.①③④⑤
二、填空题
11.已知是关于x,y的二元一次方程的一个解,那么a的值是 .
12.一只不透明的口袋中装有若干个白球,再将8个红球放入袋中,这些球除颜色外都相同.每次摸出一个球,记录颜色、放回搅匀后再摸,通过大量重复摸球试验后发现,摸到红球的频率在附近摆动,根据频率的稳定性,估计袋中的白球有 个.
13.不等式组的整数解为 .
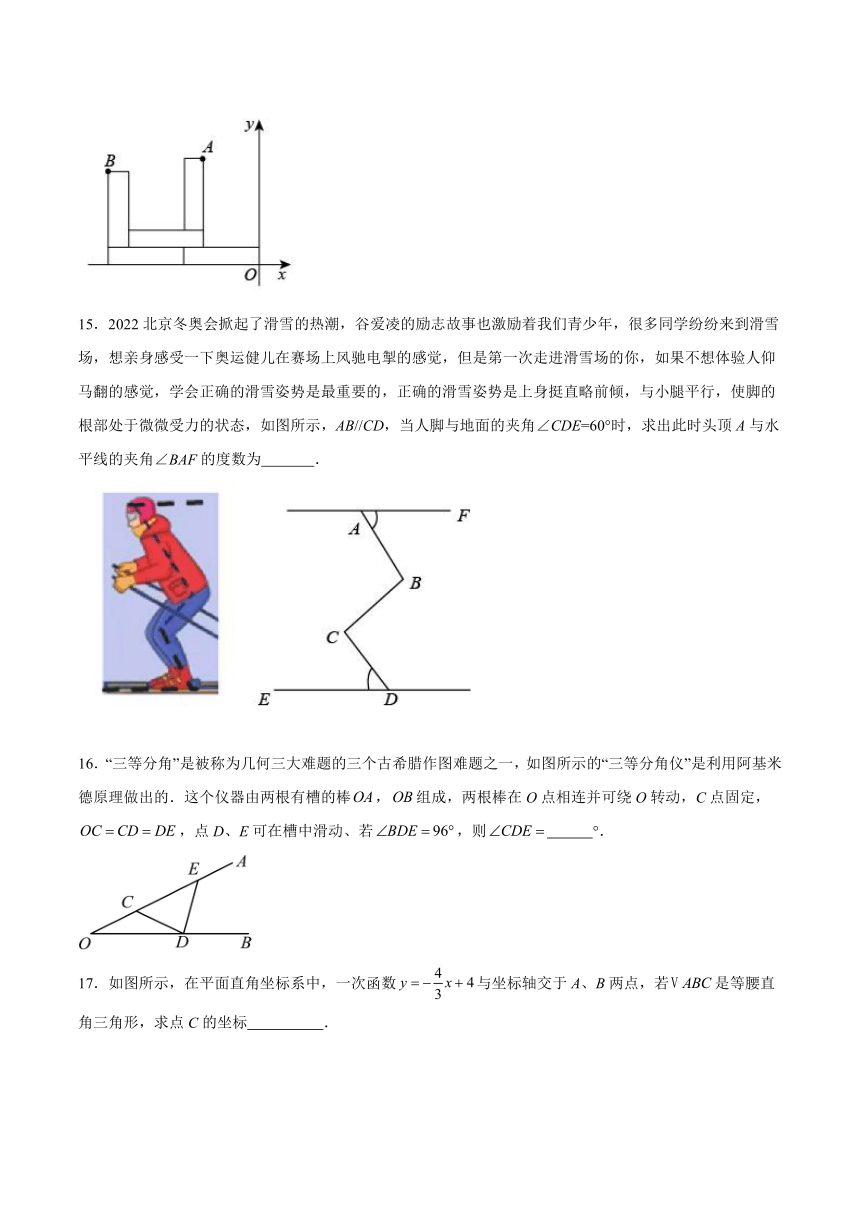
14.如图,5个大小形状完全相同的长方形纸片,在直角坐标系中摆成如图图案,已知,则点的坐标是 .
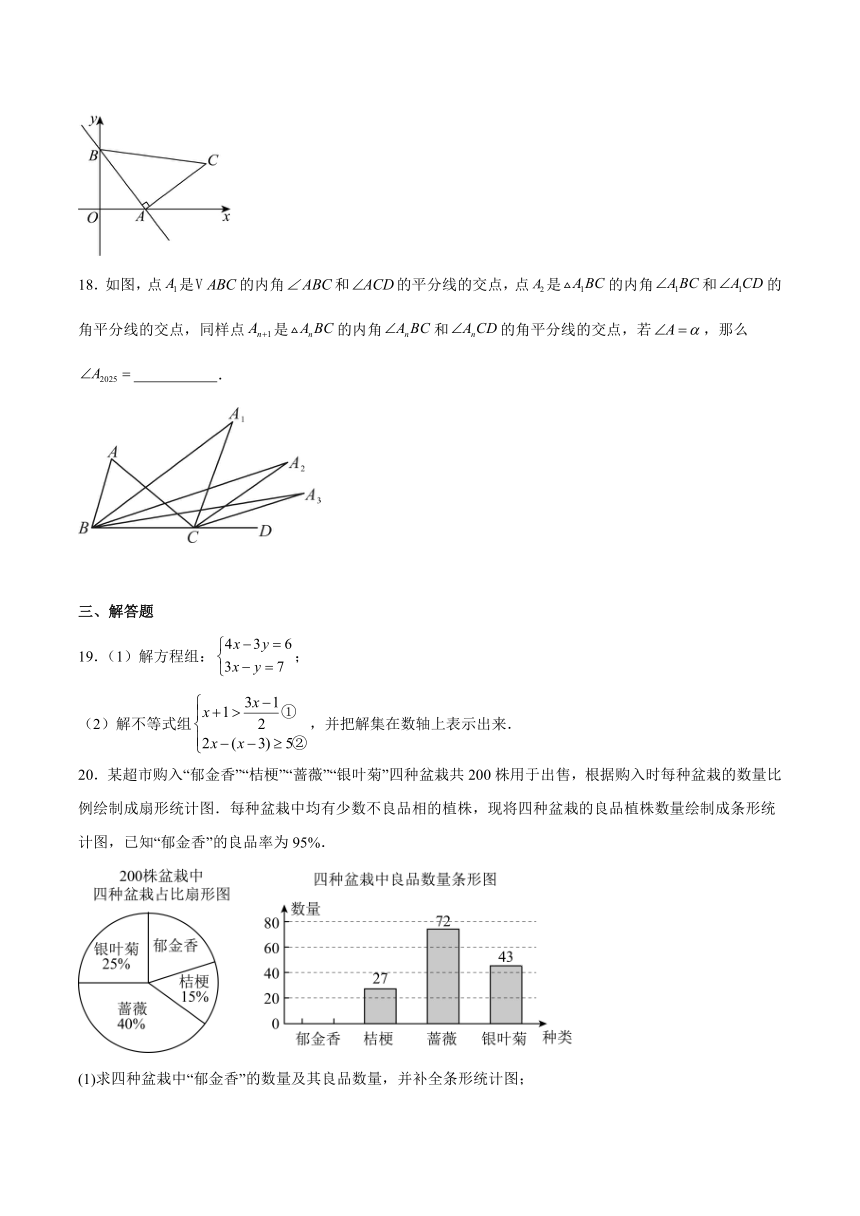
15.2022北京冬奥会掀起了滑雪的热潮,谷爱凌的励志故事也激励着我们青少年,很多同学纷纷来到滑雪场,想亲身感受一下奥运健儿在赛场上风驰电掣的感觉,但是第一次走进滑雪场的你,如果不想体验人仰马翻的感觉,学会正确的滑雪姿势是最重要的,正确的滑雪姿势是上身挺直略前倾,与小腿平行,使脚的根部处于微微受力的状态,如图所示,AB//CD,当人脚与地面的夹角∠CDE=60°时,求出此时头顶A与水平线的夹角∠BAF的度数为 .
16.“三等分角”是被称为几何三大难题的三个古希腊作图难题之一,如图所示的“三等分角仪”是利用阿基米德原理做出的.这个仪器由两根有槽的棒,组成,两根棒在O点相连并可绕O转动,C点固定,,点D、E可在槽中滑动、若,则 °.
17.如图所示,在平面直角坐标系中,一次函数与坐标轴交于A、B两点,若是等腰直角三角形,求点C的坐标 .
18.如图,点是的内角和的平分线的交点,点是的内角和的角平分线的交点,同样点是的内角和的角平分线的交点,若,那么 .
三、解答题
19.(1)解方程组:;
(2)解不等式组,并把解集在数轴上表示出来.
20.某超市购入“郁金香”“桔梗”“蔷薇”“银叶菊”四种盆栽共200株用于出售,根据购入时每种盆栽的数量比例绘制成扇形统计图.每种盆栽中均有少数不良品相的植株,现将四种盆栽的良品植株数量绘制成条形统计图,已知“郁金香”的良品率为95%.
(1)求四种盆栽中“郁金香”的数量及其良品数量,并补全条形统计图;
(2)如果从这200株盆栽中随机抽选1株,求它为良品的概率:
(3)根据市场调查,这四种盆栽的进价和售价如下:
盆栽品种 郁金香 桔梗 蔷薇 银叶菊
每株进价(元) 30 30 20 30
每株售价(元) 60 50 40 50
为了尽快卖出这批盆栽,超市对不良品相的植株在售价基础上进行8折促销.请你从四种盆栽中选择一种你喜欢的盆栽,计算这种盆栽全部售完后超市获得的利润是多少?
21.如图所示是超市购物车的侧面示意图,扶手框顶框底,车轮两支脚架.
(1)求的度数.
(2)若支脚架所在的直线垂直于,试判断与支脚架的位置关系,并说明理由.
22.根据以下学习素材,完成下列两个任务:
学习素材
素材一 某校组织学生去农场进行学农实践,体验草莓采摘、包装和销售.同学们了解到该农场在包装草莓时,通常会采用精包装和简包装两种包装方式.
素材二 精包装 简包装
每盒3斤,每盒售价35元 每盒2斤,每盒售价25元
问题解决
任务一 在活动中,学生共卖出了700斤草莓,销售总收入为8500元,请问精包装和简包装各销售了多少盒?
任务二 根据客户要求,农场现在需要分装100盒草莓,既有精包装也有简包装,分装草莓总重量不少于260斤.每个精包装盒的成本为1元,每个简包装盒的成本为元.若要将购买包装盒的成本控制在88元以内,怎么样确定分装方案才能让农场总收入最大,最大值为多少,并说明理由.
23.如图,在中,点为上一点,,点是延长线上一点,连接,点恰好在的垂直平分线上,过点作,过点作.
(1)试说明:;
(2)若,求的度数.
24.如图,在平面直角坐标系中,一次函数的图象与x轴交点为A,且与正比例函数的图象交于点C.
(1)求m 的值及一次函数 的表达式;
(2)根据图象,直接的解集是: .
(3)若P是x轴上一点,且,求点P的坐标.
25.已知在和中,,,,点D是直线上的一动点(点D不与点B,C重合),连接.
(1)在图①中,当点D在边上时,求证:;(提示:证全等)
(2)在图②中,当点D在边的延长线上时,结论是否成立?若不成立,请猜想,,之间存在的数量关系,并说明理由;猜想与的位置关系,并说明理由;
(3)在图③中,当点D在边的反向延长线上时,补全图形,不需要写证明过程,直接写出,,间存在的数量关系.
参考答案
1.D
A选项中最高次数为2次,则不是;
B选项中第二个方程不是整式方程,则不是;
C选项中含有3个未知数,则不是;
故选:D.
2.B
解:如图所示
,,
,
,,
,
故选:B.
3.D
、∵,∴,原选项不成立,此选项不符合题意;
、∵,∴,原选项不成立,此选项不符合题意;
、∵,∴或,原选项不成立,此选项不符合题意;
、∵,∴,原选项成立,此选项符合题意;
故选:.
4.D
∵铜钱的面积为4π,而中间正方形小孔的面积为1,
∴随机向铜钱上滴一滴油(油滴大小忽略不计),则油恰好落入孔中的概率是 ,
故选D.
5.B
解:如图,作于点D,
中,,,
,
,
,
故选B.
6.A
解:由图形可知,交点
当时,,
关于的不等式的解集是:,
故选:A.
7.D
解:设甲有羊只,乙有羊只,
甲得到乙的九只羊,甲的羊就比乙的羊多一倍,
;
乙得到甲的九只羊,甲、乙两家的羊一样多,
.
根据题意可得,
故选:D.
8.B
解:如图,过点作于,则,
由作图可知,是的角平分线,
∴,
∵,,
∴,
∴,,
∵,
∴,,
设,则,
在中,,
∴,
解得,
∴,
∴,
故选:B.
9.B
解:,,
,
.
,
,
在和中,
,
∴,
,,
,
故选:.
10.A
解:∵,,
∴,,
∵,
∴,
又∵,
∴,
∵,,
∴,故①正确;
∵平分,
∴,
∴;故②错误;
连接,
∵,
∴,
∴
∵,
∴垂直平分,,
∴,,故③正确;
在中,,
∴,故④错误;
∵,平分,
∴,
又∵,
∴,
∴,
∴垂直平分,
∴与成轴对称,故⑤正确;
故选:A.
11.3
解: 是关于x,y的二元一次方程的一个解,
,
解得.
故答案为:3.
12.42
解:设白球有个,
∴,
解得,,
检验,当时,原分式方程的分母不为零,
∴是原分式方程的解,
∴白球有个,
故答案为:42 .
13.
解:,
由①得:,
由②得:,
不等式组的解集为,
则不等式组的整数解为,
故答案为:.
14.
解:设长方形纸片的长和宽分别为x、y,
由题意得,
解得,
∴,
∴,
故答案为;.
15.60°/60度
解:延长AB交直线ED于点H,
∵AH∥CD,
∴∠CDE=∠DHA=60°,
∵根据题意得AF∥EH,
∴∠FAB=∠DHA=60°,
故答案为:60°.
16.52
解:,
,,
,
,
,
,
.
故答案为:52.
17.
解:当时,,解得,即点坐标为,
当时,,则点坐标为,
作垂直于轴,
∴,
∵是等腰直角三角形,
,,
,
,
,
在和中,
∴,
,,
,
,
∴点的坐标是.
故答案为:.
18.
解:∵和的平分线交于点,
∴,
∵,
∴
;
同理可得,,
…,
∴,
∴
故答案为:.
19.(1);(2),数轴见解析.
(1)解:,
得:,
得:,
解得,
把代入②:,
原方程组的解为:;
(2)解:,
解不等式①得:,
解不等式②得:,
原不等式组的解集为:.
不等式组的解集在数轴上表示为:
20.(1)40;38;见解析
(2)
(3)郁金香全部售完获得利润1176元;(答案不唯一)
(1)解:四种盆栽中“郁金香”的数量为:
(株),
良品数量掌握(株),
补全条形统计图,如图所示:
(2)解:从这200株盆栽中随机抽选1株,它为良品的概率为:
.
(3)解:郁金香全部售完后超市获得的利润为:
(元);
桔梗全部售完后超市获得的利润为:
(元);
蔷薇全部售完后超市获得的利润为:
(元);
银叶菊全部售完后超市获得的利润为:
(元).
21.(1);
(2)平行,理由见解析.
(1)解:∵,
∴ ,
又∵ ,
∴;
(2)解:∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴.
22.(1)100,200(2)精包装75盒,简包装25盒,收入最大,最大值为元.
(1)解:设精包装卖出x盒,简包装卖出y盒,
根据题意得:,
解得:.
答:精包装卖出100盒,简包装卖出200盒;
(2)解;设精包装草莓盒,则简包装草莓盒;
根据题意,得,
解得,
设总收入为y元,根据题意,得
,
又y随a的增大而增大,且a为正整数,
故时,y取得最大值,此时
故精包装75盒,简包装25盒,收入最大,最大值为元.
23.(1)见解析
(2)
(1)证明:∵点恰好在的垂直平分线上,
∴,
∵,
∴,
∴,
∵,,
∴,,
∴;
(2)解:∵,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴.
24.(1)2,
(2)
(3)或
(1)解:∵在正比例函数的图象上,
∴,解得:,
∴,
∵一次函数的图象与x轴交点为,且与正比例函数的图象交于点,
∴,解得:,
∴一次函数的表达式为;
(2)由图象可知,位于轴的右侧,在点的左侧,
∵C,
∴的解集是;
(3)设点坐标为,
∵,
∴,
解得:或,
∴点P的坐标为或.
25.(1)见解析
(2)不成立,存在的数量关系为,位置关系为,理由见解析
(3)图见解析,或
(1)证明:∵,
∴,
∴,
又∵,,
∴,
∴,
∴;
(2)解:不成立,存在的数量关系为,位置关系为,理由如下:
∵,
∴,
又∵,,
∴,
∴,,
∵,
∴,
∵,,
∴,
∴,
∴,
∴;
(3)解:①当E在下方时,如图3,
存在的数量关系为,
理由如下:
∵,
∴,
又∵,,
∴,
∴,
∴.
②当E在上方时,如图4,
存在的数量关系为,
∵,,
∴;
又∵,,
∴,
∴,,
∴;
在中,由勾股定理得,
∴.
一、单选题
1.下列方程组中是二元一次方程组的是( )
A. B. C. D.
2.已知,将含角的直角三角板如图放置,若,则的度数为( )
A. B. C. D.
3.若,则下列不等式正确的是( )
A. B.
C. D.
4.欧阳修在《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆其口,徐以构酌油之,自钱孔入,而钱不湿”,可见卖油的技艺之高超.如图,若铜钱半径为,中间有边长为的正方形小孔,随机向铜钱上滴一滴油(油滴大小忽略不计),则油恰好落入孔中的概率是( )
A. B. C. D.
5.5月26日,“2023中国国际大数据产业博览会”在贵阳开幕,在“自动化立体库”中有许多几何元素,其中有一个等腰三角形模型(示意图如图所示),它的顶角为,腰长为,则底边上的高是( )
A. B. C. D.
6.如图,若直线与直线交于一点,则关于的不等式的解集是( )
A. B. C. D.
7.我国古典数学文献《增删算法统宗·六均输》中有一个“隔沟计算”的问题:甲乙两人隔一条沟放牧,二人心里暗中合计,甲对乙说:“我得到你的九只羊,我的羊就比你多一倍.”乙对甲说:“我得到你的九只羊,咱俩家的羊一样多.”请问甲乙各有多少只羊呢?两个人在沟两边闲坐,心里很烦躁,因为在地上画了半晌,也没算出来.设甲有羊x只,乙有羊y只,则得合题意的方程组是( )
A. B.
C. D.
8.如图,在中,,,,以为圆心,适当长为半径画弧,分别交,于,两点,再分别以,为圆心,大于的长为半径画弧,两弧交于点.作射线交于点,则的面积是( )
A. B. C. D.
9.如图,,,,,垂足分别是点、,,,则的长是( )
A. B. C. D.
10.已知:如图,中,点是边上一点,,,平分,且于,与相交于点,若于,交于点.有以下结论:
①;②;③若连接,则;④点是的中点;⑤与成轴对称.以上五个结论中正确的是( )
A.①③⑤ B.①④⑤ C.①②③⑤ D.①③④⑤
二、填空题
11.已知是关于x,y的二元一次方程的一个解,那么a的值是 .
12.一只不透明的口袋中装有若干个白球,再将8个红球放入袋中,这些球除颜色外都相同.每次摸出一个球,记录颜色、放回搅匀后再摸,通过大量重复摸球试验后发现,摸到红球的频率在附近摆动,根据频率的稳定性,估计袋中的白球有 个.
13.不等式组的整数解为 .
14.如图,5个大小形状完全相同的长方形纸片,在直角坐标系中摆成如图图案,已知,则点的坐标是 .
15.2022北京冬奥会掀起了滑雪的热潮,谷爱凌的励志故事也激励着我们青少年,很多同学纷纷来到滑雪场,想亲身感受一下奥运健儿在赛场上风驰电掣的感觉,但是第一次走进滑雪场的你,如果不想体验人仰马翻的感觉,学会正确的滑雪姿势是最重要的,正确的滑雪姿势是上身挺直略前倾,与小腿平行,使脚的根部处于微微受力的状态,如图所示,AB//CD,当人脚与地面的夹角∠CDE=60°时,求出此时头顶A与水平线的夹角∠BAF的度数为 .
16.“三等分角”是被称为几何三大难题的三个古希腊作图难题之一,如图所示的“三等分角仪”是利用阿基米德原理做出的.这个仪器由两根有槽的棒,组成,两根棒在O点相连并可绕O转动,C点固定,,点D、E可在槽中滑动、若,则 °.
17.如图所示,在平面直角坐标系中,一次函数与坐标轴交于A、B两点,若是等腰直角三角形,求点C的坐标 .
18.如图,点是的内角和的平分线的交点,点是的内角和的角平分线的交点,同样点是的内角和的角平分线的交点,若,那么 .
三、解答题
19.(1)解方程组:;
(2)解不等式组,并把解集在数轴上表示出来.
20.某超市购入“郁金香”“桔梗”“蔷薇”“银叶菊”四种盆栽共200株用于出售,根据购入时每种盆栽的数量比例绘制成扇形统计图.每种盆栽中均有少数不良品相的植株,现将四种盆栽的良品植株数量绘制成条形统计图,已知“郁金香”的良品率为95%.
(1)求四种盆栽中“郁金香”的数量及其良品数量,并补全条形统计图;
(2)如果从这200株盆栽中随机抽选1株,求它为良品的概率:
(3)根据市场调查,这四种盆栽的进价和售价如下:
盆栽品种 郁金香 桔梗 蔷薇 银叶菊
每株进价(元) 30 30 20 30
每株售价(元) 60 50 40 50
为了尽快卖出这批盆栽,超市对不良品相的植株在售价基础上进行8折促销.请你从四种盆栽中选择一种你喜欢的盆栽,计算这种盆栽全部售完后超市获得的利润是多少?
21.如图所示是超市购物车的侧面示意图,扶手框顶框底,车轮两支脚架.
(1)求的度数.
(2)若支脚架所在的直线垂直于,试判断与支脚架的位置关系,并说明理由.
22.根据以下学习素材,完成下列两个任务:
学习素材
素材一 某校组织学生去农场进行学农实践,体验草莓采摘、包装和销售.同学们了解到该农场在包装草莓时,通常会采用精包装和简包装两种包装方式.
素材二 精包装 简包装
每盒3斤,每盒售价35元 每盒2斤,每盒售价25元
问题解决
任务一 在活动中,学生共卖出了700斤草莓,销售总收入为8500元,请问精包装和简包装各销售了多少盒?
任务二 根据客户要求,农场现在需要分装100盒草莓,既有精包装也有简包装,分装草莓总重量不少于260斤.每个精包装盒的成本为1元,每个简包装盒的成本为元.若要将购买包装盒的成本控制在88元以内,怎么样确定分装方案才能让农场总收入最大,最大值为多少,并说明理由.
23.如图,在中,点为上一点,,点是延长线上一点,连接,点恰好在的垂直平分线上,过点作,过点作.
(1)试说明:;
(2)若,求的度数.
24.如图,在平面直角坐标系中,一次函数的图象与x轴交点为A,且与正比例函数的图象交于点C.
(1)求m 的值及一次函数 的表达式;
(2)根据图象,直接的解集是: .
(3)若P是x轴上一点,且,求点P的坐标.
25.已知在和中,,,,点D是直线上的一动点(点D不与点B,C重合),连接.
(1)在图①中,当点D在边上时,求证:;(提示:证全等)
(2)在图②中,当点D在边的延长线上时,结论是否成立?若不成立,请猜想,,之间存在的数量关系,并说明理由;猜想与的位置关系,并说明理由;
(3)在图③中,当点D在边的反向延长线上时,补全图形,不需要写证明过程,直接写出,,间存在的数量关系.
参考答案
1.D
A选项中最高次数为2次,则不是;
B选项中第二个方程不是整式方程,则不是;
C选项中含有3个未知数,则不是;
故选:D.
2.B
解:如图所示
,,
,
,,
,
故选:B.
3.D
、∵,∴,原选项不成立,此选项不符合题意;
、∵,∴,原选项不成立,此选项不符合题意;
、∵,∴或,原选项不成立,此选项不符合题意;
、∵,∴,原选项成立,此选项符合题意;
故选:.
4.D
∵铜钱的面积为4π,而中间正方形小孔的面积为1,
∴随机向铜钱上滴一滴油(油滴大小忽略不计),则油恰好落入孔中的概率是 ,
故选D.
5.B
解:如图,作于点D,
中,,,
,
,
,
故选B.
6.A
解:由图形可知,交点
当时,,
关于的不等式的解集是:,
故选:A.
7.D
解:设甲有羊只,乙有羊只,
甲得到乙的九只羊,甲的羊就比乙的羊多一倍,
;
乙得到甲的九只羊,甲、乙两家的羊一样多,
.
根据题意可得,
故选:D.
8.B
解:如图,过点作于,则,
由作图可知,是的角平分线,
∴,
∵,,
∴,
∴,,
∵,
∴,,
设,则,
在中,,
∴,
解得,
∴,
∴,
故选:B.
9.B
解:,,
,
.
,
,
在和中,
,
∴,
,,
,
故选:.
10.A
解:∵,,
∴,,
∵,
∴,
又∵,
∴,
∵,,
∴,故①正确;
∵平分,
∴,
∴;故②错误;
连接,
∵,
∴,
∴
∵,
∴垂直平分,,
∴,,故③正确;
在中,,
∴,故④错误;
∵,平分,
∴,
又∵,
∴,
∴,
∴垂直平分,
∴与成轴对称,故⑤正确;
故选:A.
11.3
解: 是关于x,y的二元一次方程的一个解,
,
解得.
故答案为:3.
12.42
解:设白球有个,
∴,
解得,,
检验,当时,原分式方程的分母不为零,
∴是原分式方程的解,
∴白球有个,
故答案为:42 .
13.
解:,
由①得:,
由②得:,
不等式组的解集为,
则不等式组的整数解为,
故答案为:.
14.
解:设长方形纸片的长和宽分别为x、y,
由题意得,
解得,
∴,
∴,
故答案为;.
15.60°/60度
解:延长AB交直线ED于点H,
∵AH∥CD,
∴∠CDE=∠DHA=60°,
∵根据题意得AF∥EH,
∴∠FAB=∠DHA=60°,
故答案为:60°.
16.52
解:,
,,
,
,
,
,
.
故答案为:52.
17.
解:当时,,解得,即点坐标为,
当时,,则点坐标为,
作垂直于轴,
∴,
∵是等腰直角三角形,
,,
,
,
,
在和中,
∴,
,,
,
,
∴点的坐标是.
故答案为:.
18.
解:∵和的平分线交于点,
∴,
∵,
∴
;
同理可得,,
…,
∴,
∴
故答案为:.
19.(1);(2),数轴见解析.
(1)解:,
得:,
得:,
解得,
把代入②:,
原方程组的解为:;
(2)解:,
解不等式①得:,
解不等式②得:,
原不等式组的解集为:.
不等式组的解集在数轴上表示为:
20.(1)40;38;见解析
(2)
(3)郁金香全部售完获得利润1176元;(答案不唯一)
(1)解:四种盆栽中“郁金香”的数量为:
(株),
良品数量掌握(株),
补全条形统计图,如图所示:
(2)解:从这200株盆栽中随机抽选1株,它为良品的概率为:
.
(3)解:郁金香全部售完后超市获得的利润为:
(元);
桔梗全部售完后超市获得的利润为:
(元);
蔷薇全部售完后超市获得的利润为:
(元);
银叶菊全部售完后超市获得的利润为:
(元).
21.(1);
(2)平行,理由见解析.
(1)解:∵,
∴ ,
又∵ ,
∴;
(2)解:∵,
∴,
∴,
∴,
∵,
∴,
∴,
∴.
22.(1)100,200(2)精包装75盒,简包装25盒,收入最大,最大值为元.
(1)解:设精包装卖出x盒,简包装卖出y盒,
根据题意得:,
解得:.
答:精包装卖出100盒,简包装卖出200盒;
(2)解;设精包装草莓盒,则简包装草莓盒;
根据题意,得,
解得,
设总收入为y元,根据题意,得
,
又y随a的增大而增大,且a为正整数,
故时,y取得最大值,此时
故精包装75盒,简包装25盒,收入最大,最大值为元.
23.(1)见解析
(2)
(1)证明:∵点恰好在的垂直平分线上,
∴,
∵,
∴,
∴,
∵,,
∴,,
∴;
(2)解:∵,
∴,
∴,
∵,
∴,
∵,
∴,
∵,
∴.
24.(1)2,
(2)
(3)或
(1)解:∵在正比例函数的图象上,
∴,解得:,
∴,
∵一次函数的图象与x轴交点为,且与正比例函数的图象交于点,
∴,解得:,
∴一次函数的表达式为;
(2)由图象可知,位于轴的右侧,在点的左侧,
∵C,
∴的解集是;
(3)设点坐标为,
∵,
∴,
解得:或,
∴点P的坐标为或.
25.(1)见解析
(2)不成立,存在的数量关系为,位置关系为,理由见解析
(3)图见解析,或
(1)证明:∵,
∴,
∴,
又∵,,
∴,
∴,
∴;
(2)解:不成立,存在的数量关系为,位置关系为,理由如下:
∵,
∴,
又∵,,
∴,
∴,,
∵,
∴,
∵,,
∴,
∴,
∴,
∴;
(3)解:①当E在下方时,如图3,
存在的数量关系为,
理由如下:
∵,
∴,
又∵,,
∴,
∴,
∴.
②当E在上方时,如图4,
存在的数量关系为,
∵,,
∴;
又∵,,
∴,
∴,,
∴;
在中,由勾股定理得,
∴.
同课章节目录
