23.1.2行线分线段成比例 教案 华东师大版(2024)教案九年级上册
文档属性
| 名称 | 23.1.2行线分线段成比例 教案 华东师大版(2024)教案九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 171.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 19:06:47 | ||
图片预览


文档简介
2.平行线分线段成比例
1.了解平行线分线段成比例的生成过程,掌握平行线分线段成比例的内容.能应用平行线分线段成比例证明线段成比例等问题,并会进行有关的计算.
2.通过平行线分线段成比例的生成过程与应用,培养学生探索新知识、提高分析问题和解决问题的能力,提高学生的识图能力和发散思维能力,以及现有知识向新知识迁移的能力.
重点:平行线分线段成比例及其推论的应用.
难点:平行线分线段成比例的推导过程.
一组等距离的平行线在直线m上所截得的线段相等,那么在直线n上所截得的线段有什么关系
阅读教材P51~52内容,完成下列问题:
问题一:如图(1)所示,
翻开我们的作业本,每一页都是由一些间距相等的平行线组成的.
所以AB=BC,DE=EF,那么 = .
现在让我们观察一般的情况.
问题二:如图(2)所示,当m,n两条直线平行时,AD,DB,FE,EC这四条线段的长度有什么关系 我们量一量,算一算,看和是否还存在这种关系呢
解:=.
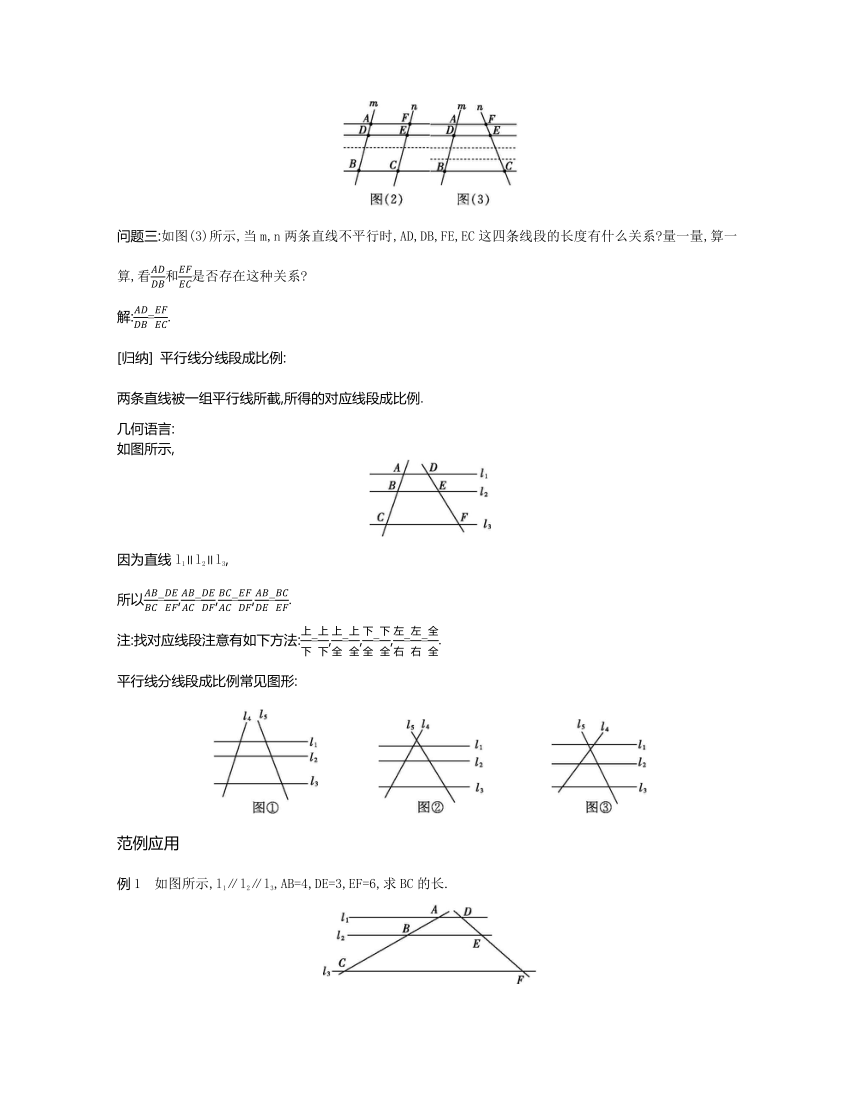
问题三:如图(3)所示,当m,n两条直线不平行时,AD,DB,FE,EC这四条线段的长度有什么关系 量一量,算一算,看和是否存在这种关系
解:=.
[归纳] 平行线分线段成比例:
两条直线被一组平行线所截,所得的对应线段成比例.
几何语言:
如图所示,
因为直线l1∥l2∥l3,
所以=,=,=,=.
注:找对应线段注意有如下方法:=,=,=,==.
平行线分线段成比例常见图形:
范例应用
例1 如图所示,l1∥l2∥l3,AB=4,DE=3,EF=6,求BC的长.
解:因为l1∥l2∥l3,所以=.
又AB=4,DE=3,EF=6,所以=.
所以BC=8.
例2 如图所示,l1∥l2∥l3,两条直线与这三条平行线分别交于点A,B,C和D,E,F.若AB=4,BC=3,DE=6,求DF的值.
解:因为l1∥l2∥l3,
所以=,即=,解得EF=.
则DF=DE+EF=.
问题四:如图所示,DE∥BC.
(1)下列各式是否正确:
=( √ ); =( √ ); =( × ); =( √ );
(2)已知=,则= .
[归纳] 平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
推论的几何语言:
如图所示,因为DE∥BC,
所以=.
范例应用
例3 如图所示,E为 ABCD的边CD延长线上的一点,连结BE,交AC于点O,交AD于点F.求证:OB∶OF=OE∶OB.
证明:因为四边形ABCD为平行四边形,
所以AB∥CD,AD∥BC.
所以OE∶OB=OC∶OA,OC∶OA=OB∶OF.
所以OB∶OF=OE∶OB.
1.如图所示,已知l1∥l2∥l3,下列比例式中错误的是(D)
A.= B.= C.= D.=
第1题图 第2题图
2.如图所示,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是(B)
A.EG=4GC B.EG=3GC C.EG=GC D.EG=2GC
3.如图所示,l1∥l2∥l3,两条直线与这三条平行线分别交于点A,B,C和D,E,F,已知=,则的值为 .
第3题图 第4题图
4.如图所示,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A,B,C都在横格线上.若线段AB=4 cm,则线段BC= 12 cm.
5.如图所示,DE∥BC,EF∥DC,求证:AD2=AB·AF.
证明:因为DE∥BC,
所以=.
因为EF∥CD,所以=.
所以=.所以AD2=AB·AF.
平行线分线段成比例
1.平行线分线段成比例:两条直线被一组平行线所截,所得的对应线段成比例.
2.平行线分线段成比例的推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
2.平行线分线段成比例
1.平行线分线段成比例.
2.平行线分线段成比例的推论.
本节课引导学生探究基本事实后,尝试归纳,理解“对应线段”数形结合,借助直观想象,在探究的过程中,不断计算比例的值,培养学生数学运算能力,推论形成的过程引导学生分析利用平行四边形性质从不同角度去说明推论成立,整个过程培养学生的逻辑推理能力.
1.了解平行线分线段成比例的生成过程,掌握平行线分线段成比例的内容.能应用平行线分线段成比例证明线段成比例等问题,并会进行有关的计算.
2.通过平行线分线段成比例的生成过程与应用,培养学生探索新知识、提高分析问题和解决问题的能力,提高学生的识图能力和发散思维能力,以及现有知识向新知识迁移的能力.
重点:平行线分线段成比例及其推论的应用.
难点:平行线分线段成比例的推导过程.
一组等距离的平行线在直线m上所截得的线段相等,那么在直线n上所截得的线段有什么关系
阅读教材P51~52内容,完成下列问题:
问题一:如图(1)所示,
翻开我们的作业本,每一页都是由一些间距相等的平行线组成的.
所以AB=BC,DE=EF,那么 = .
现在让我们观察一般的情况.
问题二:如图(2)所示,当m,n两条直线平行时,AD,DB,FE,EC这四条线段的长度有什么关系 我们量一量,算一算,看和是否还存在这种关系呢
解:=.
问题三:如图(3)所示,当m,n两条直线不平行时,AD,DB,FE,EC这四条线段的长度有什么关系 量一量,算一算,看和是否存在这种关系
解:=.
[归纳] 平行线分线段成比例:
两条直线被一组平行线所截,所得的对应线段成比例.
几何语言:
如图所示,
因为直线l1∥l2∥l3,
所以=,=,=,=.
注:找对应线段注意有如下方法:=,=,=,==.
平行线分线段成比例常见图形:
范例应用
例1 如图所示,l1∥l2∥l3,AB=4,DE=3,EF=6,求BC的长.
解:因为l1∥l2∥l3,所以=.
又AB=4,DE=3,EF=6,所以=.
所以BC=8.
例2 如图所示,l1∥l2∥l3,两条直线与这三条平行线分别交于点A,B,C和D,E,F.若AB=4,BC=3,DE=6,求DF的值.
解:因为l1∥l2∥l3,
所以=,即=,解得EF=.
则DF=DE+EF=.
问题四:如图所示,DE∥BC.
(1)下列各式是否正确:
=( √ ); =( √ ); =( × ); =( √ );
(2)已知=,则= .
[归纳] 平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
推论的几何语言:
如图所示,因为DE∥BC,
所以=.
范例应用
例3 如图所示,E为 ABCD的边CD延长线上的一点,连结BE,交AC于点O,交AD于点F.求证:OB∶OF=OE∶OB.
证明:因为四边形ABCD为平行四边形,
所以AB∥CD,AD∥BC.
所以OE∶OB=OC∶OA,OC∶OA=OB∶OF.
所以OB∶OF=OE∶OB.
1.如图所示,已知l1∥l2∥l3,下列比例式中错误的是(D)
A.= B.= C.= D.=
第1题图 第2题图
2.如图所示,DE∥FG∥BC,若DB=4FB,则EG与GC的关系是(B)
A.EG=4GC B.EG=3GC C.EG=GC D.EG=2GC
3.如图所示,l1∥l2∥l3,两条直线与这三条平行线分别交于点A,B,C和D,E,F,已知=,则的值为 .
第3题图 第4题图
4.如图所示,练习本中的横格线都平行,且相邻两条横格线间的距离都相等,同一条直线上的三个点A,B,C都在横格线上.若线段AB=4 cm,则线段BC= 12 cm.
5.如图所示,DE∥BC,EF∥DC,求证:AD2=AB·AF.
证明:因为DE∥BC,
所以=.
因为EF∥CD,所以=.
所以=.所以AD2=AB·AF.
平行线分线段成比例
1.平行线分线段成比例:两条直线被一组平行线所截,所得的对应线段成比例.
2.平行线分线段成比例的推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例.
2.平行线分线段成比例
1.平行线分线段成比例.
2.平行线分线段成比例的推论.
本节课引导学生探究基本事实后,尝试归纳,理解“对应线段”数形结合,借助直观想象,在探究的过程中,不断计算比例的值,培养学生数学运算能力,推论形成的过程引导学生分析利用平行四边形性质从不同角度去说明推论成立,整个过程培养学生的逻辑推理能力.
