初中数学华东师大版九年级上册 23.5 位似图形 教学设计
文档属性
| 名称 | 初中数学华东师大版九年级上册 23.5 位似图形 教学设计 |
|
|
| 格式 | docx | ||
| 文件大小 | 380.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 21:23:42 | ||
图片预览

文档简介
23.5 位似图形
1.了解位似图形及其有关概念,了解位似与相似的联系和区别,掌握位似图形的性质.
2.掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小.
3.能简单利用位似图形的性质解决问题.
重点:理解位似图形的概念,能利用位似的方法将一个图形放大或缩小.
难点:能利用位似图形的性质解决问题.
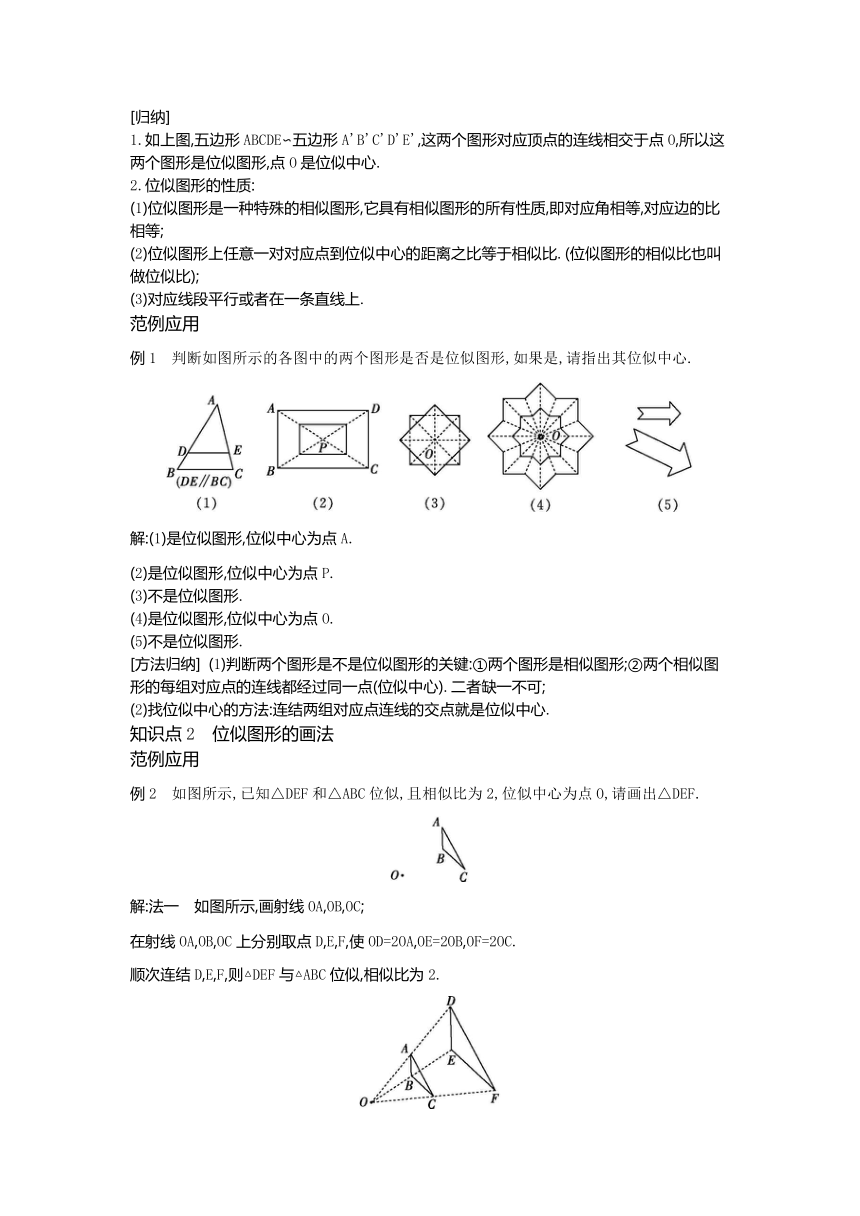
下列是一些图的变换,请连线:
我们发现:前三个图中的两个图形都是全等的,而第四个图形中的两个图形相似,那么第四个图是怎样的一种变换呢
知识点1 位似图形的概念
阅读教材P80~81内容,完成下列问题.
下面介绍一种特殊的画相似多边形的方法.
现在要把多边形ABCDE放大到1.5倍,也就是使所得的多边形与原多边形的相似比为1.5.如图所示,我们可以按下列步骤画出所需的多边形:
1.任取一点O.
2.以点O为端点作射线OA,OB,OC,OD和OE.
3.分别在射线OA,OB,OC,OD和OE上取点A',B',C',D'和E',使OA'∶OA=OB'∶OB=OC'∶OC=OD'∶OD=OE'∶OE=1.5.
4.顺次连结点A',B',C',D'和E',就得到所要画的多边形A'B'C'D'E'.
定义:两个多边形不仅相似,而且对应顶点的连线相交于一点,各组对应顶点到该点的距离之比相等,像这样的两个图形叫做位似图形,这点叫做位似中心.
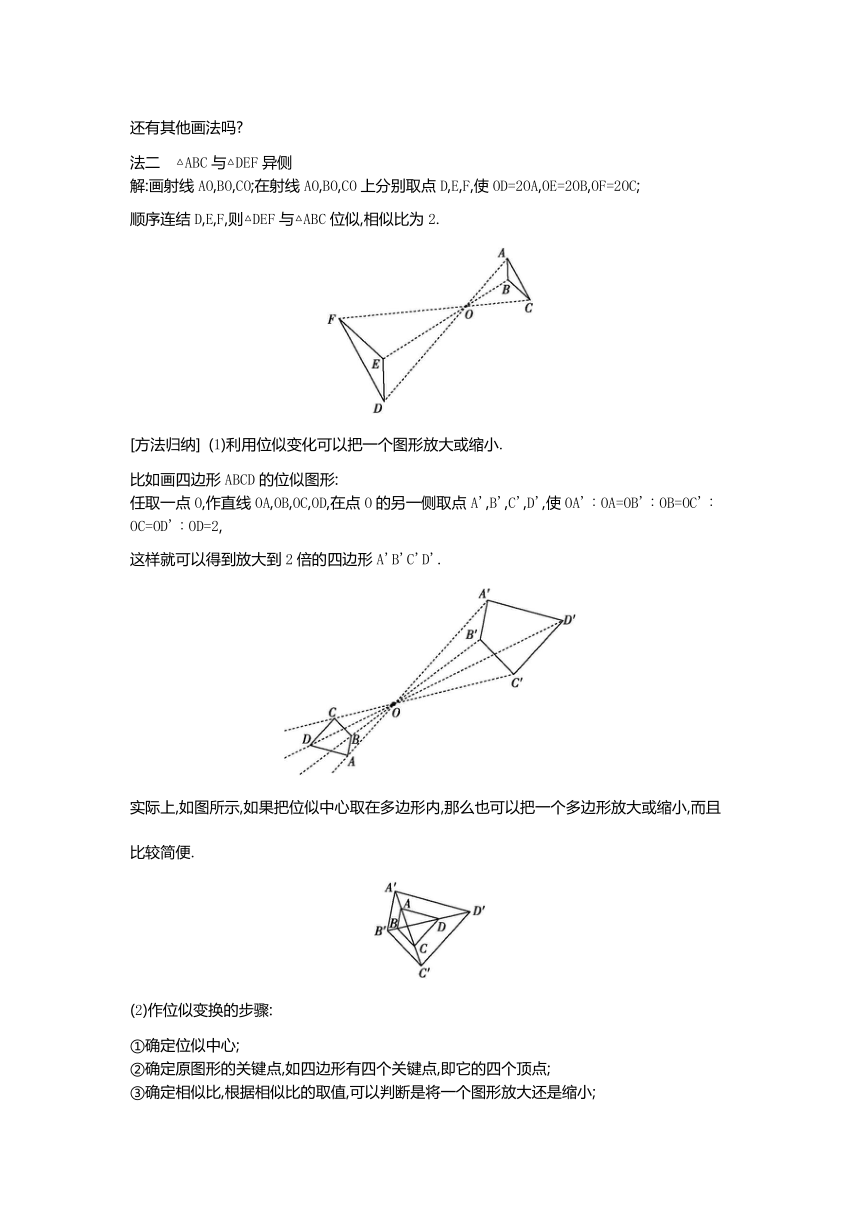
[归纳]
1.如上图,五边形ABCDE∽五边形A'B'C'D'E',这两个图形对应顶点的连线相交于点O,所以这两个图形是位似图形,点O是位似中心.
2.位似图形的性质:
(1)位似图形是一种特殊的相似图形,它具有相似图形的所有性质,即对应角相等,对应边的比相等;
(2)位似图形上任意一对对应点到位似中心的距离之比等于相似比.(位似图形的相似比也叫做位似比);
(3)对应线段平行或者在一条直线上.
范例应用
例1 判断如图所示的各图中的两个图形是否是位似图形,如果是,请指出其位似中心.
解:(1)是位似图形,位似中心为点A.
(2)是位似图形,位似中心为点P.
(3)不是位似图形.
(4)是位似图形,位似中心为点O.
(5)不是位似图形.
[方法归纳] (1)判断两个图形是不是位似图形的关键:①两个图形是相似图形;②两个相似图形的每组对应点的连线都经过同一点(位似中心).二者缺一不可;
(2)找位似中心的方法:连结两组对应点连线的交点就是位似中心.
知识点2 位似图形的画法
范例应用
例2 如图所示,已知△DEF和△ABC位似,且相似比为2,位似中心为点O,请画出△DEF.
解:法一 如图所示,画射线OA,OB,OC;
在射线OA,OB,OC上分别取点D,E,F,使OD=2OA,OE=2OB,OF=2OC.
顺次连结D,E,F,则△DEF与△ABC位似,相似比为2.
还有其他画法吗
法二 △ABC与△DEF异侧
解:画射线AO,BO,CO;在射线AO,BO,CO上分别取点D,E,F,使OD=2OA,OE=2OB,OF=2OC;
顺序连结D,E,F,则△DEF与△ABC位似,相似比为2.
[方法归纳] (1)利用位似变化可以把一个图形放大或缩小.
比如画四边形ABCD的位似图形:
任取一点O,作直线OA,OB,OC,OD,在点O的另一侧取点A',B',C',D',使OA'∶OA=OB'∶OB=OC'∶OC=OD'∶OD=2,
这样就可以得到放大到2倍的四边形A'B'C'D'.
实际上,如图所示,如果把位似中心取在多边形内,那么也可以把一个多边形放大或缩小,而且比较简便.
(2)作位似变换的步骤:
①确定位似中心;
②确定原图形的关键点,如四边形有四个关键点,即它的四个顶点;
③确定相似比,根据相似比的取值,可以判断是将一个图形放大还是缩小;
④找到对应点,顺次连结,即可得到位似变换后的图形.
(3)符合要求的图形不唯一,因为所作的图形与所确定的位似中心的位置有关,并且同一个位似中心的两侧各有一个符合要求的图形.
1.如图所示的两个四边形是位似图形,它们的位似中心是(D)
A.点M B.点N C.点O D.点P
2.下列关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于相似比.其中正确的是(A)
A.②③ B.①② C.③④ D.②③④
3.如图所示,点O是五边形ABCDE和五边形A1B1C1D1E1的位似中心,若OA∶OA1=1∶3,则C1D1∶CD等于(C)
A.1∶2 B.1∶3 C.3∶1 D.1∶4
4.△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,点A的对应点A'的坐标为 (4,6)或(-4,-6) .
5.如图所示,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB'C'D',使它与四边形ABCD位似,且相似比为2.在图中画出四边形AB'C'D'.
解:如图所示.
6.如图所示,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的格点上.
(1)画出位似中心点O;
(2)求出△ABC与△A'B'C'的相似比;
(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的相似比等于1.5.
解:(1)如图所示,分别作射线C'C、B'B,交于点O,则点O就是要求作的位似中心.
(2)因为BC==,B'C'==2,
所以△ABC与△A'B'C'的相似比为∶2=1∶2.
(3)如图所示,作射线OA,在OA,OB,OC上依次取点A1,B1,C1,使===1.5,顺次连结点A1,B1,C1,所得到的
△A1B1C1就是符合要求的图形.
位似图形
1.位似图形的概念.
2.位似图形的性质.
3.画位似图形.
4.判断是不是位似图形,找位似中心.
23.5 位似图形
1.位似图形的概念
(1)相似图形
(2)对应点连线交于一点
(3)对应边的比等于相似比
2.利用位似把图形放大或缩小,一般有2种情况.
“切身体验”是本节课的重要学习途径,要动手操作,动脑研究操作过程,还要将理论联系实际,同时要分析不同作法的区别与联系.每个学生都是在一系列“切身体验”中自主找到利用位似多边形的相关知识放大或缩小图形的方法的.课堂的教学过程也通过学生的“切身体验”,实现了以学生为主体,由教师为主导,将知识融入到个体体验中的目的,同时也体现了新课改的理念.
1.了解位似图形及其有关概念,了解位似与相似的联系和区别,掌握位似图形的性质.
2.掌握位似图形的画法,能够利用作位似图形的方法将一个图形放大或缩小.
3.能简单利用位似图形的性质解决问题.
重点:理解位似图形的概念,能利用位似的方法将一个图形放大或缩小.
难点:能利用位似图形的性质解决问题.
下列是一些图的变换,请连线:
我们发现:前三个图中的两个图形都是全等的,而第四个图形中的两个图形相似,那么第四个图是怎样的一种变换呢
知识点1 位似图形的概念
阅读教材P80~81内容,完成下列问题.
下面介绍一种特殊的画相似多边形的方法.
现在要把多边形ABCDE放大到1.5倍,也就是使所得的多边形与原多边形的相似比为1.5.如图所示,我们可以按下列步骤画出所需的多边形:
1.任取一点O.
2.以点O为端点作射线OA,OB,OC,OD和OE.
3.分别在射线OA,OB,OC,OD和OE上取点A',B',C',D'和E',使OA'∶OA=OB'∶OB=OC'∶OC=OD'∶OD=OE'∶OE=1.5.
4.顺次连结点A',B',C',D'和E',就得到所要画的多边形A'B'C'D'E'.
定义:两个多边形不仅相似,而且对应顶点的连线相交于一点,各组对应顶点到该点的距离之比相等,像这样的两个图形叫做位似图形,这点叫做位似中心.
[归纳]
1.如上图,五边形ABCDE∽五边形A'B'C'D'E',这两个图形对应顶点的连线相交于点O,所以这两个图形是位似图形,点O是位似中心.
2.位似图形的性质:
(1)位似图形是一种特殊的相似图形,它具有相似图形的所有性质,即对应角相等,对应边的比相等;
(2)位似图形上任意一对对应点到位似中心的距离之比等于相似比.(位似图形的相似比也叫做位似比);
(3)对应线段平行或者在一条直线上.
范例应用
例1 判断如图所示的各图中的两个图形是否是位似图形,如果是,请指出其位似中心.
解:(1)是位似图形,位似中心为点A.
(2)是位似图形,位似中心为点P.
(3)不是位似图形.
(4)是位似图形,位似中心为点O.
(5)不是位似图形.
[方法归纳] (1)判断两个图形是不是位似图形的关键:①两个图形是相似图形;②两个相似图形的每组对应点的连线都经过同一点(位似中心).二者缺一不可;
(2)找位似中心的方法:连结两组对应点连线的交点就是位似中心.
知识点2 位似图形的画法
范例应用
例2 如图所示,已知△DEF和△ABC位似,且相似比为2,位似中心为点O,请画出△DEF.
解:法一 如图所示,画射线OA,OB,OC;
在射线OA,OB,OC上分别取点D,E,F,使OD=2OA,OE=2OB,OF=2OC.
顺次连结D,E,F,则△DEF与△ABC位似,相似比为2.
还有其他画法吗
法二 △ABC与△DEF异侧
解:画射线AO,BO,CO;在射线AO,BO,CO上分别取点D,E,F,使OD=2OA,OE=2OB,OF=2OC;
顺序连结D,E,F,则△DEF与△ABC位似,相似比为2.
[方法归纳] (1)利用位似变化可以把一个图形放大或缩小.
比如画四边形ABCD的位似图形:
任取一点O,作直线OA,OB,OC,OD,在点O的另一侧取点A',B',C',D',使OA'∶OA=OB'∶OB=OC'∶OC=OD'∶OD=2,
这样就可以得到放大到2倍的四边形A'B'C'D'.
实际上,如图所示,如果把位似中心取在多边形内,那么也可以把一个多边形放大或缩小,而且比较简便.
(2)作位似变换的步骤:
①确定位似中心;
②确定原图形的关键点,如四边形有四个关键点,即它的四个顶点;
③确定相似比,根据相似比的取值,可以判断是将一个图形放大还是缩小;
④找到对应点,顺次连结,即可得到位似变换后的图形.
(3)符合要求的图形不唯一,因为所作的图形与所确定的位似中心的位置有关,并且同一个位似中心的两侧各有一个符合要求的图形.
1.如图所示的两个四边形是位似图形,它们的位似中心是(D)
A.点M B.点N C.点O D.点P
2.下列关于位似图形的表述:①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于相似比.其中正确的是(A)
A.②③ B.①② C.③④ D.②③④
3.如图所示,点O是五边形ABCDE和五边形A1B1C1D1E1的位似中心,若OA∶OA1=1∶3,则C1D1∶CD等于(C)
A.1∶2 B.1∶3 C.3∶1 D.1∶4
4.△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,点A的对应点A'的坐标为 (4,6)或(-4,-6) .
5.如图所示,在10×10的正方形网格中,点A,B,C,D均在格点上,以点A为位似中心画四边形AB'C'D',使它与四边形ABCD位似,且相似比为2.在图中画出四边形AB'C'D'.
解:如图所示.
6.如图所示,图中的小方格都是边长为1的正方形,△ABC与△A'B'C'是以点O为位似中心的位似图形,它们的顶点都在小正方形的格点上.
(1)画出位似中心点O;
(2)求出△ABC与△A'B'C'的相似比;
(3)以点O为位似中心,再画一个△A1B1C1,使它与△ABC的相似比等于1.5.
解:(1)如图所示,分别作射线C'C、B'B,交于点O,则点O就是要求作的位似中心.
(2)因为BC==,B'C'==2,
所以△ABC与△A'B'C'的相似比为∶2=1∶2.
(3)如图所示,作射线OA,在OA,OB,OC上依次取点A1,B1,C1,使===1.5,顺次连结点A1,B1,C1,所得到的
△A1B1C1就是符合要求的图形.
位似图形
1.位似图形的概念.
2.位似图形的性质.
3.画位似图形.
4.判断是不是位似图形,找位似中心.
23.5 位似图形
1.位似图形的概念
(1)相似图形
(2)对应点连线交于一点
(3)对应边的比等于相似比
2.利用位似把图形放大或缩小,一般有2种情况.
“切身体验”是本节课的重要学习途径,要动手操作,动脑研究操作过程,还要将理论联系实际,同时要分析不同作法的区别与联系.每个学生都是在一系列“切身体验”中自主找到利用位似多边形的相关知识放大或缩小图形的方法的.课堂的教学过程也通过学生的“切身体验”,实现了以学生为主体,由教师为主导,将知识融入到个体体验中的目的,同时也体现了新课改的理念.
