1.1同底数幂的除法 课件(共28张PPT) 北师大版(2024)数学七年级下册
文档属性
| 名称 | 1.1同底数幂的除法 课件(共28张PPT) 北师大版(2024)数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 29.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 21:32:00 | ||
图片预览








文档简介
(共28张PPT)
同底数幂的除法
时间:
主讲人:
2025.7
2025
年 级:七年级 学 科:数学(北师版)
目录
课程导入
01
知识讲解
02
应用实践
03
总结拓展
04
CONTENTS
课堂练习
05
课程导入
Part.
01
幂运算不仅是数学中的基础概念,更是科技和日常生活中的常见工具。从计算机存储容量的计算到生物种群增长的模型,幂运算无处不在。例如,计算机的存储单位从KB到TB,每增加一个单位都是以2的幂次方增长,这种增长方式直观地展示了幂运算在科技领域的应用价值。
幂运算在科技与生活中的应用
生活中的幂运算现象
复习导入
1.同底数幂乘法法则:
2.幂的乘方法则:
(m,n都是正整数)
3.积的乘方法则:
(n是正整数)
(m,n都是正整数)
引入新课
一种液体每升含有 1012 个有害细菌。为了试验某种灭菌剂的效果,科学家进行了实验,发现 1 滴灭菌剂可以杀死 109 个有害细菌。要将 1 L 液体中的有害细菌全部杀死, 需要这种灭菌剂多少滴 你是怎样计算的
1012÷109
同底数幂的除法
同底数的幂相除,怎样计算呢
观察这个算式,它有何特点
是相同底数的幂相除。
知识讲解
Part.
02
从具体实例到一般规律
逆用同底数幂乘法推导
在讲解同底数幂的除法法则时,可以通过具体的实例来引导学生发现规律。例如,计算(a5 a3)时,学生可以通过约分的方式,发现结果实际上是(a5- 3=a2)。这种从具体到一般的推理过程,不仅帮助学生记忆法则,更重要的是培养了他们的逻辑思维能力和数学直觉。
同底数幂的除法法则可以看作是同底数幂乘法法则的逆过程。通过复习同底数幂的乘法法则,学生可以更容易地理解除法法则的推导过程。例如,已知(amⅹ an = am+n),那么(am+n an = am),这样的逆向思维训练有助于学生加深对数学法则的理解和记忆。
同底数幂除法的法则推导
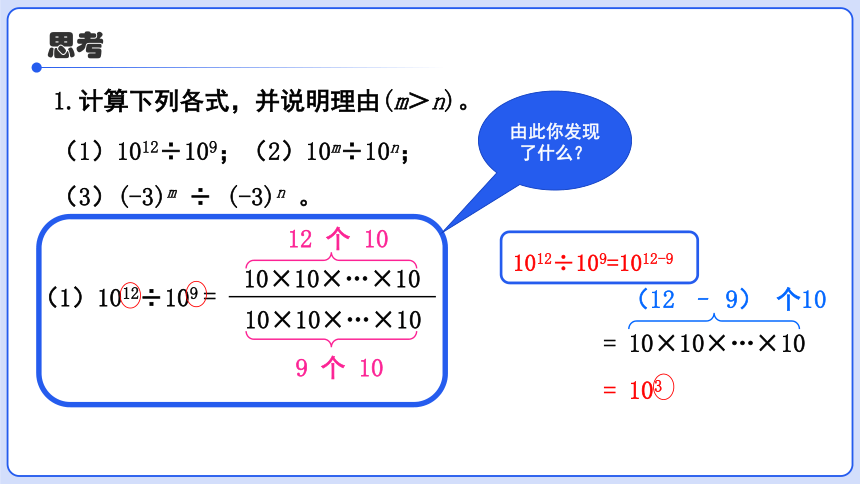
思考
1.计算下列各式,并说明理由(m>n)。
(1)1012÷109;(2)10m÷10n;
(3)(-3)m ÷ (-3)n 。
(1)1012÷109
12 个 10
=
10×10×…×10
10×10×…×10
9 个 10
由此你发现了什么?
= 103
= 10×10×…×10
(12 – 9) 个10
1012÷109=1012-9
思考
1.计算下列各式,并说明理由(m>n)。
(1)1012÷109;(2)10m÷10n;
(3)(-3)m ÷ (-3)n 。
由此你发现了什么?
(2)10m÷10n
m 个 10
=
10×10×…×10
10×10×…×10
n 个 10
= 10m – n
= 10×10×…×10
(m – n) 个 10
10m÷10n=10m-n
思考
1.计算下列各式,并说明理由(m>n)。
(1)1012÷109;(2)10m÷10n;
(3)(-3)m ÷ (-3)n 。
由此你发现了什么?
(3)(– 3)m÷ (– 3) n
=
(– 3) × (– 3) ×…× (– 3)
(– 3) × (– 3) ×…× (– 3)
n 个 (– 3)
m 个 (– 3)
= (– 3) m – n
= (– 3) × (– 3) ×…× (– 3)
(m – n) 个 (– 3)
(-3)m÷(-3) n=(-3)m-n
公式推导
2.如果m,n都是正整数,且m>n,那么am÷an等于什么 你是怎样得到的
am÷an
m 个 a
=
a · a · … · a
a · a · … · a
n 个 a
= am – n
= a · a · … · a
(m – n) 个 a
即am÷an= am – n(m>n,且m,n都是正整数)
应用实践
Part.
03
例5 计算
(1) a7÷a4; (2) (– x)6÷(– x)3;
(3) (xy)4÷(xy); (4) b2m+2÷b2 。
解:(1) a7÷a4 = a7 – 4 = a3;
(2) (– x)6÷(– x)3 = (– x)6 – 3 = (– x)3 = – x3;
(3) (xy)4÷(xy) = (xy)4–1 = (xy)3 = x3y3 ;
(4) b2m+2÷b2 = b2m+2–2 = b2m 。
01
同底数幂除法的直接应用
在基础计算题型中,需要直接应用同底数幂的除法法则进行计算。例如,计算(x7 x4)时,应能够迅速得出结果为(x7- 4=x3)。通过大量的练习,可以熟练掌握这一法则,并能够在不同的题目情境中灵活运用,提高解题的准确性和速度。
基础计算题型训练
思考
解:(1)23÷23 = = 1,
(2)a3÷a3 = = 1。
(1)23÷23=23-3=20,
(2)a3÷a3=a3-3=a0,
20=1
a0=1
根据除法意义计算:
根据同底数幂除法法则计算:
你能得出什么结论
(1)23÷23;(2)a3÷a3。
思考
我们规定:
任何一个不等于0的数的0次幂都等于1。
数学语言:
a0=1(a≠0)
注意:零指数幂的底数可以是单项式,也可以是多项式,但是不能为0。
思考
23÷25 = = ,
a3÷a5 = = 。
23÷25=23-5=2-2,
a3÷a5=a3-5=a-2。
=2-2
=a-2
根据除法意义计算:
根据同底数幂除法法则计算:
你能得出什么结论
(1)23÷25;(2)a3÷a5。
思考
我们规定:
任何不等于零的数的-p(p是正整数)次幂等于这个数的p次幂的倒数。
同底数幂的除法法则:
数学语言:
a-p=(a≠0)
am ÷ an = am – n(a ≠ 0,m,n 都是正整数)
例6 计算
用小数或分数表示下列各数:
(1)10 –3;(2)70×8 –2;(3)1.6×10 –4 。
解:(1) ;
(2) ;
(3)
思考
有的细胞的直径只有 1 微米(μm),
即 0.000 001 m;
某种计算机完成一次基本运算的时间约为 1纳秒(ns), 即 0.000 000 001 s;
一个氧原子的质量为
0.000 000 000 000 000 000 000 000 026 57 kg 。
你能用负指数表示这些数吗
思考
用科学记数法可以很方便地表示一些绝对值较大的数,同样,用科学记数法也可以很方便地表示一些绝对值较小的数。
因为
= 10 – 1 ;
= 10 – 2;
= 10 – 3 ……
思考
0.000 001 = = 1×10 – 6,
0.000 000 001 = = 1×10 – 9,
0.000 000 000 000 000 000 000 000 026 57
= 2.657× = 2.657×10 – 26 。
思考
一般地,一个小于 1 的正数可以表示为
a× 10n的形式, 其中 1 ≤ a < 10, n 是负整数。
大于-1的负数也可以用类似的方法表示,如-0.000 002 56=-2.56×10-6。
总结拓展
Part.
04
在课程的最后,需要对同底数幂的运算进行综合回顾,帮助学生梳理知识体系。通过总结同底数幂的乘法、除法法则,以及它们之间的联系,学生可以形成一个完整的知识网络。这样的梳理不仅有助于巩固所学知识,也为后续学习更复杂的数学概念打下坚实的基础。
同底数幂运算的综合回顾
幂运算作为数学中的基础概念,其应用范围远不止于初中数学。在课程的拓展部分,可以介绍幂运算在高中数学、物理、计算机科学等领域的应用,激发学生的学习兴趣和探索欲望。例如,可以简要介绍指数函数、对数函数等高级概念,为学生未来的学习指明方向。
幂运算的拓展学习方向
知识体系梳理
课堂练习
Part.
05
练一练
(1)(xy2)6m (xy2)m
(2)(b-a)6 (a-b)3
(3)已知am=3,an=2,求a2m-3n的值。
同底数幂的除法
时间:
主讲人:
2025.7
2025
年 级:七年级 学 科:数学(北师版)
目录
课程导入
01
知识讲解
02
应用实践
03
总结拓展
04
CONTENTS
课堂练习
05
课程导入
Part.
01
幂运算不仅是数学中的基础概念,更是科技和日常生活中的常见工具。从计算机存储容量的计算到生物种群增长的模型,幂运算无处不在。例如,计算机的存储单位从KB到TB,每增加一个单位都是以2的幂次方增长,这种增长方式直观地展示了幂运算在科技领域的应用价值。
幂运算在科技与生活中的应用
生活中的幂运算现象
复习导入
1.同底数幂乘法法则:
2.幂的乘方法则:
(m,n都是正整数)
3.积的乘方法则:
(n是正整数)
(m,n都是正整数)
引入新课
一种液体每升含有 1012 个有害细菌。为了试验某种灭菌剂的效果,科学家进行了实验,发现 1 滴灭菌剂可以杀死 109 个有害细菌。要将 1 L 液体中的有害细菌全部杀死, 需要这种灭菌剂多少滴 你是怎样计算的
1012÷109
同底数幂的除法
同底数的幂相除,怎样计算呢
观察这个算式,它有何特点
是相同底数的幂相除。
知识讲解
Part.
02
从具体实例到一般规律
逆用同底数幂乘法推导
在讲解同底数幂的除法法则时,可以通过具体的实例来引导学生发现规律。例如,计算(a5 a3)时,学生可以通过约分的方式,发现结果实际上是(a5- 3=a2)。这种从具体到一般的推理过程,不仅帮助学生记忆法则,更重要的是培养了他们的逻辑思维能力和数学直觉。
同底数幂的除法法则可以看作是同底数幂乘法法则的逆过程。通过复习同底数幂的乘法法则,学生可以更容易地理解除法法则的推导过程。例如,已知(amⅹ an = am+n),那么(am+n an = am),这样的逆向思维训练有助于学生加深对数学法则的理解和记忆。
同底数幂除法的法则推导
思考
1.计算下列各式,并说明理由(m>n)。
(1)1012÷109;(2)10m÷10n;
(3)(-3)m ÷ (-3)n 。
(1)1012÷109
12 个 10
=
10×10×…×10
10×10×…×10
9 个 10
由此你发现了什么?
= 103
= 10×10×…×10
(12 – 9) 个10
1012÷109=1012-9
思考
1.计算下列各式,并说明理由(m>n)。
(1)1012÷109;(2)10m÷10n;
(3)(-3)m ÷ (-3)n 。
由此你发现了什么?
(2)10m÷10n
m 个 10
=
10×10×…×10
10×10×…×10
n 个 10
= 10m – n
= 10×10×…×10
(m – n) 个 10
10m÷10n=10m-n
思考
1.计算下列各式,并说明理由(m>n)。
(1)1012÷109;(2)10m÷10n;
(3)(-3)m ÷ (-3)n 。
由此你发现了什么?
(3)(– 3)m÷ (– 3) n
=
(– 3) × (– 3) ×…× (– 3)
(– 3) × (– 3) ×…× (– 3)
n 个 (– 3)
m 个 (– 3)
= (– 3) m – n
= (– 3) × (– 3) ×…× (– 3)
(m – n) 个 (– 3)
(-3)m÷(-3) n=(-3)m-n
公式推导
2.如果m,n都是正整数,且m>n,那么am÷an等于什么 你是怎样得到的
am÷an
m 个 a
=
a · a · … · a
a · a · … · a
n 个 a
= am – n
= a · a · … · a
(m – n) 个 a
即am÷an= am – n(m>n,且m,n都是正整数)
应用实践
Part.
03
例5 计算
(1) a7÷a4; (2) (– x)6÷(– x)3;
(3) (xy)4÷(xy); (4) b2m+2÷b2 。
解:(1) a7÷a4 = a7 – 4 = a3;
(2) (– x)6÷(– x)3 = (– x)6 – 3 = (– x)3 = – x3;
(3) (xy)4÷(xy) = (xy)4–1 = (xy)3 = x3y3 ;
(4) b2m+2÷b2 = b2m+2–2 = b2m 。
01
同底数幂除法的直接应用
在基础计算题型中,需要直接应用同底数幂的除法法则进行计算。例如,计算(x7 x4)时,应能够迅速得出结果为(x7- 4=x3)。通过大量的练习,可以熟练掌握这一法则,并能够在不同的题目情境中灵活运用,提高解题的准确性和速度。
基础计算题型训练
思考
解:(1)23÷23 = = 1,
(2)a3÷a3 = = 1。
(1)23÷23=23-3=20,
(2)a3÷a3=a3-3=a0,
20=1
a0=1
根据除法意义计算:
根据同底数幂除法法则计算:
你能得出什么结论
(1)23÷23;(2)a3÷a3。
思考
我们规定:
任何一个不等于0的数的0次幂都等于1。
数学语言:
a0=1(a≠0)
注意:零指数幂的底数可以是单项式,也可以是多项式,但是不能为0。
思考
23÷25 = = ,
a3÷a5 = = 。
23÷25=23-5=2-2,
a3÷a5=a3-5=a-2。
=2-2
=a-2
根据除法意义计算:
根据同底数幂除法法则计算:
你能得出什么结论
(1)23÷25;(2)a3÷a5。
思考
我们规定:
任何不等于零的数的-p(p是正整数)次幂等于这个数的p次幂的倒数。
同底数幂的除法法则:
数学语言:
a-p=(a≠0)
am ÷ an = am – n(a ≠ 0,m,n 都是正整数)
例6 计算
用小数或分数表示下列各数:
(1)10 –3;(2)70×8 –2;(3)1.6×10 –4 。
解:(1) ;
(2) ;
(3)
思考
有的细胞的直径只有 1 微米(μm),
即 0.000 001 m;
某种计算机完成一次基本运算的时间约为 1纳秒(ns), 即 0.000 000 001 s;
一个氧原子的质量为
0.000 000 000 000 000 000 000 000 026 57 kg 。
你能用负指数表示这些数吗
思考
用科学记数法可以很方便地表示一些绝对值较大的数,同样,用科学记数法也可以很方便地表示一些绝对值较小的数。
因为
= 10 – 1 ;
= 10 – 2;
= 10 – 3 ……
思考
0.000 001 = = 1×10 – 6,
0.000 000 001 = = 1×10 – 9,
0.000 000 000 000 000 000 000 000 026 57
= 2.657× = 2.657×10 – 26 。
思考
一般地,一个小于 1 的正数可以表示为
a× 10n的形式, 其中 1 ≤ a < 10, n 是负整数。
大于-1的负数也可以用类似的方法表示,如-0.000 002 56=-2.56×10-6。
总结拓展
Part.
04
在课程的最后,需要对同底数幂的运算进行综合回顾,帮助学生梳理知识体系。通过总结同底数幂的乘法、除法法则,以及它们之间的联系,学生可以形成一个完整的知识网络。这样的梳理不仅有助于巩固所学知识,也为后续学习更复杂的数学概念打下坚实的基础。
同底数幂运算的综合回顾
幂运算作为数学中的基础概念,其应用范围远不止于初中数学。在课程的拓展部分,可以介绍幂运算在高中数学、物理、计算机科学等领域的应用,激发学生的学习兴趣和探索欲望。例如,可以简要介绍指数函数、对数函数等高级概念,为学生未来的学习指明方向。
幂运算的拓展学习方向
知识体系梳理
课堂练习
Part.
05
练一练
(1)(xy2)6m (xy2)m
(2)(b-a)6 (a-b)3
(3)已知am=3,an=2,求a2m-3n的值。
同课章节目录
