3.4 相似三角形的判定与性质 同步练习(含答案)
文档属性
| 名称 | 3.4 相似三角形的判定与性质 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 577.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-21 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
3.4 相似三角形的判定与性质
一、单选题
1.(2024九上·吉安月考)如图,在中,,分别在和上,且.下列结论错误的是( )
A. B. C. D.
2.(2024九上·双峰期末)如图,添加以下哪个条件,仍不能直接证明与相似 ( )
A. B. C. D.
3.(2024九上·德化期末)如图,是的中位线,若的面积为,则为四边形的面积( )
A.8 B.10 C.12 D.14
4.(2022九上·衡山期末)如图,已知在,为上一点,连结,不能判断的是( )
A. B. C. D.
5.(2023九上·覃塘期中)下列说法错误的是( )
A.所有的等边三角形都相似 B.所有的正方形都相似
C.两个矩形一定不相似 D.两个菱形不一定相似
6.(2021九上·犍为期末)如图,在△ABC中,中线BE、CF相交于点G,连接EF,下列结论错误的是( )
A. B.
C. D.
7.(2017九上·文安期末)如同,在△ABC中,点D,E分别在边AB,AC上,下列条件中不能判断△ABC∽△AED的是( )
A. B. C.∠ADE=∠C D.∠AED=∠B
8.(2023·遵义模拟)如图,正方形网格中每个小正方形的边长均为,其中,B、C、D、E四点都在网格的格点上,则的面积为( )
A. B. C. D.
9.如图,△ABC中,点DE分别是ABAC的中点,则下列结论:①BC=2DE;②△ADE∽△ABC;③.其中正确的有( )
A.3个 B.2个 C.1个 D.0个
10.(2024九上·西湖月考)如图,在矩形中,,点分别在线段和线段的延长线上.若,则的长为( )
A. B. C. D.
二、填空题
11.(2024九上·贵州期中)如图,在中,,点D在边上,点E在边上且.只需添加一个条件即可证明,这个条件可以是(写出一个即可).
12.(2024九上·甘州月考)如图,在中,对角线,相交于点O,点E为的中点,交于点F.若,则的长为 .
13.相似三角形对应高的比、对应中线的比、对应角平分线的比都等于 .
14.(2020八下·香坊期末)如图,将矩形ABCD沿AE折叠,使点D落在BC边的点F处,过F作FG∥CD交AE于点G,连接DG.若AG=3 ,FG=5,则AE的长为 .
15.(2024八下·苏州工业园月考)如图,大小为4×4的正方形方格中,能作出与△ABC相似的格点三角形(顶点都在正方形的顶点上),其中最小的一个面积是 .
16.(2024·浙江模拟)如图,在中,,,点P在反比例函数图象上,,且y轴平分,则 .
三、计算题
17.(2025九下·清城开学考)如图,在中,于点D,,求和.
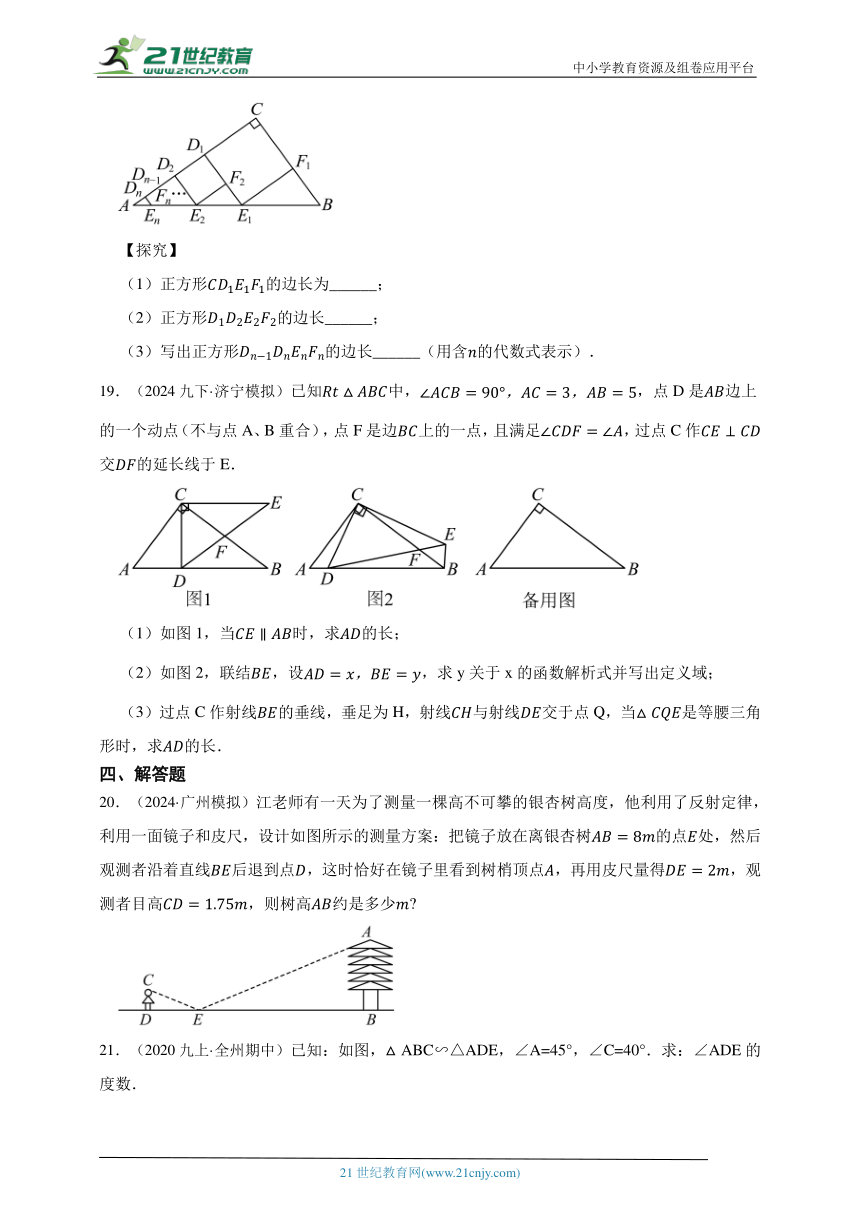
18.(2024·青岛模拟)在中,,,,依次作正方形,正方形,正方形,…,正方形,顶点,,,…,在边上,顶点,,,…,在边上.
【探究】
(1)正方形的边长为______;
(2)正方形的边长______;
(3)写出正方形的边长______(用含的代数式表示).
19.(2024九下·济宁模拟)已知中,,点D是边上的一个动点(不与点A、B重合),点F是边上的一点,且满足,过点C作交的延长线于E.
(1)如图1,当时,求的长;
(2)如图2,联结,设,求y关于x的函数解析式并写出定义域;
(3)过点C作射线的垂线,垂足为H,射线与射线交于点Q,当是等腰三角形时,求的长.
四、解答题
20.(2024·广州模拟)江老师有一天为了测量一棵高不可攀的银杏树高度,他利用了反射定律,利用一面镜子和皮尺,设计如图所示的测量方案:把镜子放在离银杏树的点处,然后观测者沿着直线后退到点,这时恰好在镜子里看到树梢顶点,再用皮尺量得,观测者目高,则树高约是多少
21.(2020九上·全州期中)已知:如图,△ABC∽△ADE,∠A=45°,∠C=40°.求:∠ADE的度数.
22.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
23.(2022九上·宁波期中)如图①,在Rt△ABC中,∠B=90°,AB=5,BC=12,CD=5,DE∥AB.将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)①当α=0°时,= ;②当α=180°时,= .
(2)试判断:当0≤α≤360°时,的大小有无变化?请仅就图②的情形给出证明.
(3)当△EDC旋转到A,D,E三点共线时,直接写出线段BD的长.
答案解析部分
1.【答案】B
【知识点】两条直线被一组平行线所截,所得的对应线段成比例;相似三角形的判定与性质
2.【答案】D
【知识点】相似三角形的判定
3.【答案】C
【知识点】相似三角形的判定与性质;三角形的中位线定理
4.【答案】D
【知识点】相似三角形的判定
5.【答案】C
【知识点】矩形的性质;正方形的性质;相似三角形的判定
6.【答案】D
【知识点】相似三角形的判定与性质;三角形的中位线定理
7.【答案】A
【知识点】相似三角形的判定
8.【答案】C
【知识点】平行线的性质;三角形的面积;相似三角形的判定与性质
9.【答案】A
【知识点】相似三角形的判定与性质;三角形的中位线定理
10.【答案】B
【知识点】等腰三角形的判定与性质;矩形的性质;相似三角形的判定与性质
11.【答案】
【知识点】相似三角形的判定
12.【答案】3
【知识点】平行四边形的性质;相似三角形的判定与性质
13.【答案】相似比
【知识点】相似三角形的性质
14.【答案】
【知识点】翻折变换(折叠问题);相似三角形的判定与性质
15.【答案】
【知识点】正方形的性质;相似三角形的性质;作图﹣相似变换
16.【答案】
【知识点】待定系数法求反比例函数解析式;轴对称的性质;相似三角形的判定与性质
17.【答案】,
【知识点】勾股定理;相似三角形的判定与性质
18.【答案】(1);
(2);
(3).
【知识点】相似三角形的判定与性质
19.【答案】(1)
(2)函数关系式为,定义域为
(3)
【知识点】平行线的判定与性质;勾股定理;相似三角形的判定与性质;等腰三角形的概念
20.【答案】
【知识点】相似三角形的判定与性质
21.【答案】解答:∵△ABC∽△ADE,∠C=40°,∴∠AED=∠C=40°.在△ADE中,∵∠AED+∠ADE+∠A=180°,∠A=45°即40°+∠ADE+45°=180°,∴∠ADE=95°.
【知识点】相似三角形的性质
22.【答案】解:(1)∵∠ACB=90°,AC=3,BC=4,
∴AB= =5.
∵AD=5t,CE=3t,
∴当AD=AB时,5t=5,即t=1;
∴AE=AC+CE=3+3t=6,DE=6﹣5=1.
(2)∵EF=BC=4,G是EF的中点,
∴GE=2.
当AD<AE(即t<)时,DE=AE﹣AD=3+3t﹣5t=3﹣2t,
若△DEG与△ACB相似,则 或 ,
∴=或 =,
∴t=或t= ;
当AD>AE(即t>)时,DE=AD﹣AE=5t﹣(3+3t)=2t﹣3,
若△DEG与△ACB相似,则 或 ,
∴=或 =,
解得t=或t=;
综上所述,当t=或 或 或 时,△DEG与△ACB相似.
【知识点】相似三角形的判定
23.【答案】(1);
(2)解:当0°≤α<90°时,的大小没有变化,
∵∠ECD=∠ACB,
∴∠ECA=∠DCB,
又∵=,
∴△ECA∽△DCB,
∴=.
(3)解:BD=
【知识点】相似三角形的判定与性质;图形的旋转
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.4 相似三角形的判定与性质
一、单选题
1.(2024九上·吉安月考)如图,在中,,分别在和上,且.下列结论错误的是( )
A. B. C. D.
2.(2024九上·双峰期末)如图,添加以下哪个条件,仍不能直接证明与相似 ( )
A. B. C. D.
3.(2024九上·德化期末)如图,是的中位线,若的面积为,则为四边形的面积( )
A.8 B.10 C.12 D.14
4.(2022九上·衡山期末)如图,已知在,为上一点,连结,不能判断的是( )
A. B. C. D.
5.(2023九上·覃塘期中)下列说法错误的是( )
A.所有的等边三角形都相似 B.所有的正方形都相似
C.两个矩形一定不相似 D.两个菱形不一定相似
6.(2021九上·犍为期末)如图,在△ABC中,中线BE、CF相交于点G,连接EF,下列结论错误的是( )
A. B.
C. D.
7.(2017九上·文安期末)如同,在△ABC中,点D,E分别在边AB,AC上,下列条件中不能判断△ABC∽△AED的是( )
A. B. C.∠ADE=∠C D.∠AED=∠B
8.(2023·遵义模拟)如图,正方形网格中每个小正方形的边长均为,其中,B、C、D、E四点都在网格的格点上,则的面积为( )
A. B. C. D.
9.如图,△ABC中,点DE分别是ABAC的中点,则下列结论:①BC=2DE;②△ADE∽△ABC;③.其中正确的有( )
A.3个 B.2个 C.1个 D.0个
10.(2024九上·西湖月考)如图,在矩形中,,点分别在线段和线段的延长线上.若,则的长为( )
A. B. C. D.
二、填空题
11.(2024九上·贵州期中)如图,在中,,点D在边上,点E在边上且.只需添加一个条件即可证明,这个条件可以是(写出一个即可).
12.(2024九上·甘州月考)如图,在中,对角线,相交于点O,点E为的中点,交于点F.若,则的长为 .
13.相似三角形对应高的比、对应中线的比、对应角平分线的比都等于 .
14.(2020八下·香坊期末)如图,将矩形ABCD沿AE折叠,使点D落在BC边的点F处,过F作FG∥CD交AE于点G,连接DG.若AG=3 ,FG=5,则AE的长为 .
15.(2024八下·苏州工业园月考)如图,大小为4×4的正方形方格中,能作出与△ABC相似的格点三角形(顶点都在正方形的顶点上),其中最小的一个面积是 .
16.(2024·浙江模拟)如图,在中,,,点P在反比例函数图象上,,且y轴平分,则 .
三、计算题
17.(2025九下·清城开学考)如图,在中,于点D,,求和.
18.(2024·青岛模拟)在中,,,,依次作正方形,正方形,正方形,…,正方形,顶点,,,…,在边上,顶点,,,…,在边上.
【探究】
(1)正方形的边长为______;
(2)正方形的边长______;
(3)写出正方形的边长______(用含的代数式表示).
19.(2024九下·济宁模拟)已知中,,点D是边上的一个动点(不与点A、B重合),点F是边上的一点,且满足,过点C作交的延长线于E.
(1)如图1,当时,求的长;
(2)如图2,联结,设,求y关于x的函数解析式并写出定义域;
(3)过点C作射线的垂线,垂足为H,射线与射线交于点Q,当是等腰三角形时,求的长.
四、解答题
20.(2024·广州模拟)江老师有一天为了测量一棵高不可攀的银杏树高度,他利用了反射定律,利用一面镜子和皮尺,设计如图所示的测量方案:把镜子放在离银杏树的点处,然后观测者沿着直线后退到点,这时恰好在镜子里看到树梢顶点,再用皮尺量得,观测者目高,则树高约是多少
21.(2020九上·全州期中)已知:如图,△ABC∽△ADE,∠A=45°,∠C=40°.求:∠ADE的度数.
22.如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
23.(2022九上·宁波期中)如图①,在Rt△ABC中,∠B=90°,AB=5,BC=12,CD=5,DE∥AB.将△EDC绕点C按顺时针方向旋转,记旋转角为α.
(1)①当α=0°时,= ;②当α=180°时,= .
(2)试判断:当0≤α≤360°时,的大小有无变化?请仅就图②的情形给出证明.
(3)当△EDC旋转到A,D,E三点共线时,直接写出线段BD的长.
答案解析部分
1.【答案】B
【知识点】两条直线被一组平行线所截,所得的对应线段成比例;相似三角形的判定与性质
2.【答案】D
【知识点】相似三角形的判定
3.【答案】C
【知识点】相似三角形的判定与性质;三角形的中位线定理
4.【答案】D
【知识点】相似三角形的判定
5.【答案】C
【知识点】矩形的性质;正方形的性质;相似三角形的判定
6.【答案】D
【知识点】相似三角形的判定与性质;三角形的中位线定理
7.【答案】A
【知识点】相似三角形的判定
8.【答案】C
【知识点】平行线的性质;三角形的面积;相似三角形的判定与性质
9.【答案】A
【知识点】相似三角形的判定与性质;三角形的中位线定理
10.【答案】B
【知识点】等腰三角形的判定与性质;矩形的性质;相似三角形的判定与性质
11.【答案】
【知识点】相似三角形的判定
12.【答案】3
【知识点】平行四边形的性质;相似三角形的判定与性质
13.【答案】相似比
【知识点】相似三角形的性质
14.【答案】
【知识点】翻折变换(折叠问题);相似三角形的判定与性质
15.【答案】
【知识点】正方形的性质;相似三角形的性质;作图﹣相似变换
16.【答案】
【知识点】待定系数法求反比例函数解析式;轴对称的性质;相似三角形的判定与性质
17.【答案】,
【知识点】勾股定理;相似三角形的判定与性质
18.【答案】(1);
(2);
(3).
【知识点】相似三角形的判定与性质
19.【答案】(1)
(2)函数关系式为,定义域为
(3)
【知识点】平行线的判定与性质;勾股定理;相似三角形的判定与性质;等腰三角形的概念
20.【答案】
【知识点】相似三角形的判定与性质
21.【答案】解答:∵△ABC∽△ADE,∠C=40°,∴∠AED=∠C=40°.在△ADE中,∵∠AED+∠ADE+∠A=180°,∠A=45°即40°+∠ADE+45°=180°,∴∠ADE=95°.
【知识点】相似三角形的性质
22.【答案】解:(1)∵∠ACB=90°,AC=3,BC=4,
∴AB= =5.
∵AD=5t,CE=3t,
∴当AD=AB时,5t=5,即t=1;
∴AE=AC+CE=3+3t=6,DE=6﹣5=1.
(2)∵EF=BC=4,G是EF的中点,
∴GE=2.
当AD<AE(即t<)时,DE=AE﹣AD=3+3t﹣5t=3﹣2t,
若△DEG与△ACB相似,则 或 ,
∴=或 =,
∴t=或t= ;
当AD>AE(即t>)时,DE=AD﹣AE=5t﹣(3+3t)=2t﹣3,
若△DEG与△ACB相似,则 或 ,
∴=或 =,
解得t=或t=;
综上所述,当t=或 或 或 时,△DEG与△ACB相似.
【知识点】相似三角形的判定
23.【答案】(1);
(2)解:当0°≤α<90°时,的大小没有变化,
∵∠ECD=∠ACB,
∴∠ECA=∠DCB,
又∵=,
∴△ECA∽△DCB,
∴=.
(3)解:BD=
【知识点】相似三角形的判定与性质;图形的旋转
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
