3.5 相似三角形的应用 同步练习(含答案)
文档属性
| 名称 | 3.5 相似三角形的应用 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 911.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-21 11:43:03 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
3.5 相似三角形的应用
一、单选题
1.(2024九上·泰安月考)小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为,坡面上的影长为,已知斜坡的坡角为,同一时刻,一根长为且垂直于地面放置的标杆在地面上的影长为,则树的高度为( )
A. B. C. D.
2.(2024·高平模拟)《海岛算经》是我国杰出数学家刘徽留给后世最宝贵的数学遗产.书中第一问的大致意思是:如图,要测量海岛上一座山峰的高度,立两根等高的标杆,,点,,在同一直线上,从点,处退行到点,处观察点.已知,,,的长,就可推算出山峰的高度.想要解决这一问题,需要利用( )
A.全等三角形 B.相似三角形 C.勾股定理 D.垂径定理
3.(2023九上·南海月考)据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了“小孔成像”实验,阐释了光的直线传播原理.小孔成像的示意图如图所示,光线经过小孔O,物体AB在幕布上形成倒立的实像CD.若物体AB的高为6cm,小孔O到物体和实像的水平距离BE,CE分别为8cm,6cm,则实像CD的高度为( )
A.4cm B.4.5cm C.5cm D.6cm
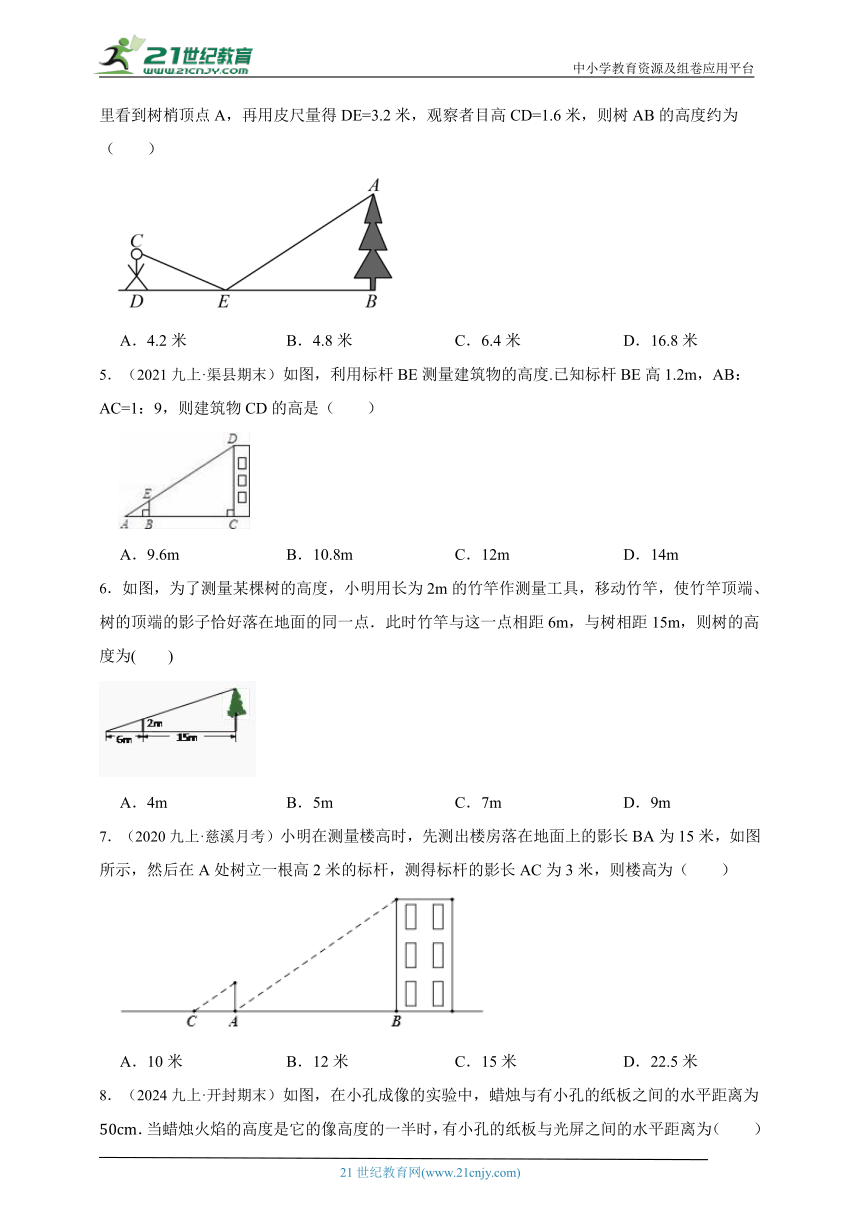
4.(2024九下·淅川月考)如图,为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组根据光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子水平放置在离树底B端8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,则树AB的高度约为( )
A.4.2米 B.4.8米 C.6.4米 D.16.8米
5.(2021九上·渠县期末)如图,利用标杆BE测量建筑物的高度.已知标杆BE高1.2m,AB:AC=1:9,则建筑物CD的高是( )
A.9.6m B.10.8m C.12m D.14m
6.如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端、树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距6m,与树相距15m,则树的高度为( )
A.4m B.5m C.7m D.9m
7.(2020九上·慈溪月考)小明在测量楼高时,先测出楼房落在地面上的影长BA为15米,如图所示,然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( )
A.10米 B.12米 C.15米 D.22.5米
8.(2024九上·开封期末)如图,在小孔成像的实验中,蜡烛与有小孔的纸板之间的水平距离为.当蜡烛火焰的高度是它的像高度的一半时,有小孔的纸板与光屏之间的水平距离为( )
A. B. C. D.
9.如图所示,一张等腰三角形纸片,底边长18cm,底边上的高长18cm,现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.第4张 B.第5张 C.第6张 D.第7张
10.(2022九上·榆树期中)如图 ABCD,F为BC中点,延长AD至E,使 ,连结EF交DC于点G,则 =( )
A.2:3 B.3:2 C.9:4 D.4:9
二、填空题
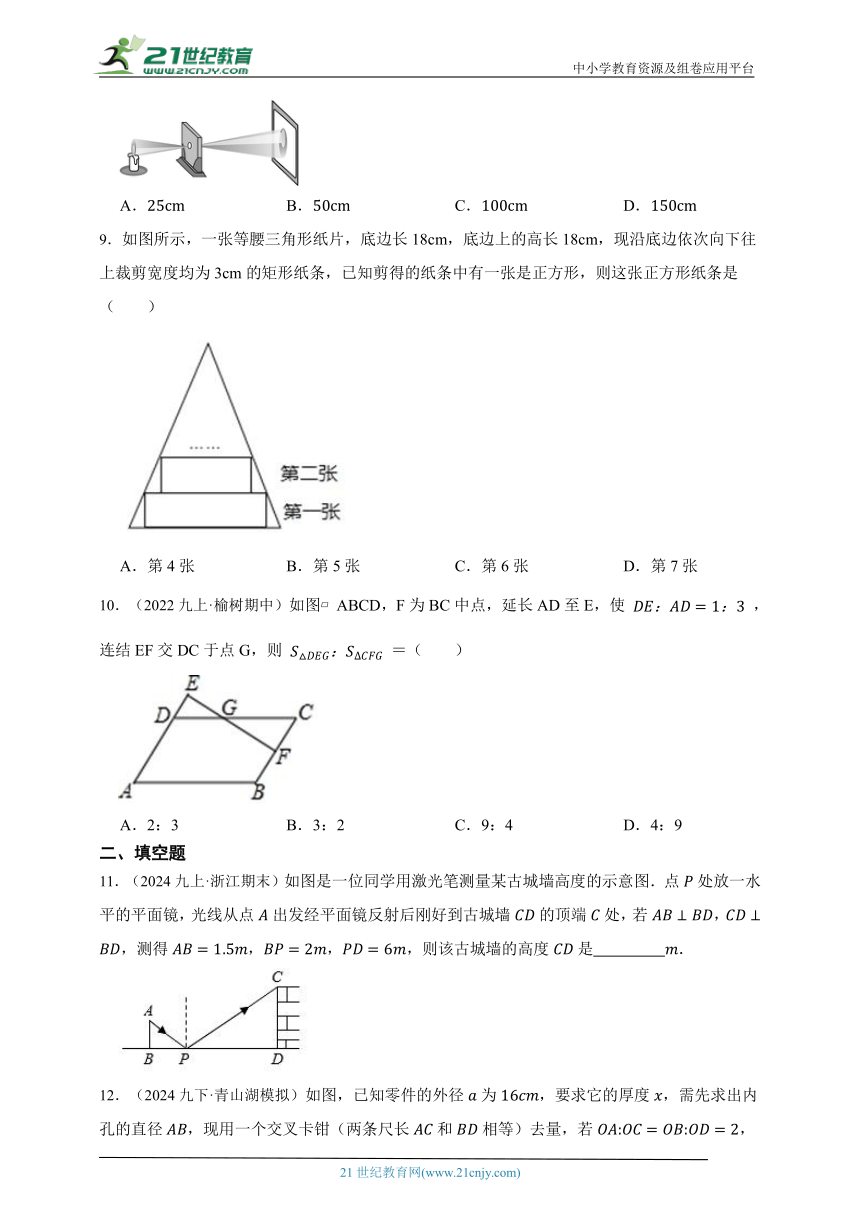
11.(2024九上·浙江期末)如图是一位同学用激光笔测量某古城墙高度的示意图.点处放一水平的平面镜,光线从点出发经平面镜反射后刚好到古城墙的顶端处,若,,测得,,,则该古城墙的高度是 .
12.(2024九下·青山湖模拟)如图,已知零件的外径为,要求它的厚度,需先求出内孔的直径,现用一个交叉卡钳(两条尺长和相等)去量,若,且量得,则厚度 .
13.(2024七上·邵阳月考)如图所示,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径为,桌面距离地面,若灯泡距离地面,则地面上阴影部分的面积为 .
14.(2022九下·普陀期中)如图,中,E是边AD的中点,BE交对角线AC于点F,那么S△AFB :S四边形FEDC的值为
15.(2023九上·萧山期中)甲、乙两同学测量一棵树的高度,在阳光下,甲同学测得一根1米长的竹竿的影长为0.8米,同时,乙同学测量时,发现树的影子不全落在地面上,如图,有一部分影子落在教学楼的墙壁上,其影长CD=1.2米,落在地面上的影长BC=2.4米,则树高AB的长是 米.
16.(2022·番禺模拟)如图,将 ABCD绕点A逆时针旋转到 AB′C′D′的位置,使点B′落在BC上,B′C′与CD交于点E.若AB=3,BC=4,BB′=1,则CE的长为 .
三、计算题
17.(2023九上·法库期中)某“综合与实践”小组开展了测量本校旗杆高度的实践活动,如图,他们在旗杆底部所在的平地上放置一个平面镜E来测量学校旗杆的高度,镜子中心E与旗杆的距离米,当镜子中心E与测量者的距离米时,测量者刚好从镜子中看到旗杆顶部的端点A.已知测量者的身高为1.6米,测量者的眼睛距地面的高度为1.5米.
(1)在计算过程中C、D之间的距离应是______米;
(2)根据以上测量结果,求出学校旗杆的高度.
18.(2024八下·苏州工业园月考)为了加快城市发展,保障市民出行方便,某市在流经该市的河流上架起一座桥,连通南北,铺就城市繁荣之路.小明和小颖想通过自己所学的数学知识计算该桥AF的长.如图,该桥两侧河岸平行,他们在河的对岸选定一个目标作为点A,再在河岸的这一边选出点B和点C,分别在AB、AC的延长线上取点D、E,使得DEBC.经测量,BC=120米,DE=210米,且点E到河岸BC的距离为60米.已知AF⊥BC于点F,请你根据提供的数据,帮助他们计算桥AF的长度.
四、解答题
19.(2024九下·石嘴山月考)如图,路灯(点)距地面8米,身高1.6米的小明从距路灯的底部(点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
20.(2023九上·金台期中)如图①,“丝绸之路群雕”刻画和表达了一队来往于丝路中途的中外混合的骆驼商旅,已成为西安著名的城市标志之一.为了测量群雕某处的高度,小明和晓璐带着平面镜和皮尺去进行测量.测量过程如下:如图②,首先,小明在处放置了一面平面镜,然后沿后退,当小明蹲在点处时恰好能在平面镜中看到雕塑顶端的像,此时小明的眼睛到地面的距离米,米;然后小明在处起立站直,晓璐眼睛贴地观察发现地面上点、小明头顶和顶端重合,测得小明的身高米,米,,,点、、、在同一条水平线上,点在上,请你求出该处雕塑的高.(平面镜的大小、厚度忽略不计,晓璐眼睛贴地观察时眼睛到地面的距离忽略不计)
21.(2017·西安模拟)某学校的学生为了对小雁塔有基本的认识,在老师的带领下对小雁塔进行了测量.测量方法如下:如图,间接测得小雁塔地部点D到地面上一点E的距离为115.2米,小雁塔的顶端为点B,且BD⊥DE,在点E处竖直放一个木棒,其顶端为C,CE=1.72米,在DE的延长线上找一点A,使A、C、B三点在同一直线上,测得AE=4.8米.求小雁塔的高度.
22.(2023九上·黄岛期中)已知不等臂跷跷板的长为3米,当的一端点碰到地面时(如图1),点离地高1.5米;当的另一端点碰到地面时(如图2),点离地高1米,求跷跷板的支撑点到地面的距离。
答案解析部分
1.【答案】A
【知识点】相似三角形的性质;相似三角形的应用
2.【答案】B
【知识点】相似三角形的应用
3.【答案】B
【知识点】相似三角形的应用
4.【答案】A
【知识点】相似三角形的应用
5.【答案】B
【知识点】相似三角形的应用
6.【答案】C
【知识点】相似三角形的应用
7.【答案】A
【知识点】相似三角形的应用
8.【答案】C
【知识点】相似三角形的应用
9.【答案】B
【知识点】相似三角形的应用
10.【答案】D
【知识点】相似三角形的判定与性质;相似三角形的应用
11.【答案】4.5
【知识点】相似三角形的应用
12.【答案】2
【知识点】相似三角形的应用
13.【答案】
【知识点】相似三角形的应用
14.【答案】
【知识点】三角形的面积;两条直线被一组平行线所截,所得的对应线段成比例;相似三角形的应用
15.【答案】4.2
【知识点】相似三角形的应用
16.【答案】
【知识点】三角形的面积;勾股定理的应用;相似三角形的应用
17.【答案】(1)1.5
(2)15米
【知识点】相似三角形的判定;相似三角形的应用
18.【答案】桥AF的长度为80米.
【知识点】相似三角形的应用
19.【答案】从点走到点,身影的长度是变短了
【知识点】相似三角形的应用
20.【答案】该处雕塑的高为7米.
【知识点】相似三角形的应用
21.【答案】解:由题意可得:△AEC∽△ADB,
则 = ,
故 = ,
解得:DB=43,
答:小雁塔的高度为43m
【知识点】相似三角形的应用
22.【答案】解:解:由题意可得,,,
∴,
在与中,
,
∴∴即∴
在与中,
,∴
∴即∴
∵∴∴
答:跷跷板的支撑点到地面的距离为0.6米.
【知识点】相似三角形的判定与性质;相似三角形的应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
3.5 相似三角形的应用
一、单选题
1.(2024九上·泰安月考)小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上,如图,此时测得地面上的影长为,坡面上的影长为,已知斜坡的坡角为,同一时刻,一根长为且垂直于地面放置的标杆在地面上的影长为,则树的高度为( )
A. B. C. D.
2.(2024·高平模拟)《海岛算经》是我国杰出数学家刘徽留给后世最宝贵的数学遗产.书中第一问的大致意思是:如图,要测量海岛上一座山峰的高度,立两根等高的标杆,,点,,在同一直线上,从点,处退行到点,处观察点.已知,,,的长,就可推算出山峰的高度.想要解决这一问题,需要利用( )
A.全等三角形 B.相似三角形 C.勾股定理 D.垂径定理
3.(2023九上·南海月考)据《墨经》记载,在两千多年前,我国学者墨子和他的学生做了“小孔成像”实验,阐释了光的直线传播原理.小孔成像的示意图如图所示,光线经过小孔O,物体AB在幕布上形成倒立的实像CD.若物体AB的高为6cm,小孔O到物体和实像的水平距离BE,CE分别为8cm,6cm,则实像CD的高度为( )
A.4cm B.4.5cm C.5cm D.6cm
4.(2024九下·淅川月考)如图,为了测量校园水平地面上一棵不可攀的树的高度,学校数学兴趣小组根据光的反射定律,利用一面镜子和一根皮尺,设计如下图所示的测量方案:把一面很小的镜子水平放置在离树底B端8.4米的点E处,然后沿着直线BE后退到点D,这时恰好在镜子里看到树梢顶点A,再用皮尺量得DE=3.2米,观察者目高CD=1.6米,则树AB的高度约为( )
A.4.2米 B.4.8米 C.6.4米 D.16.8米
5.(2021九上·渠县期末)如图,利用标杆BE测量建筑物的高度.已知标杆BE高1.2m,AB:AC=1:9,则建筑物CD的高是( )
A.9.6m B.10.8m C.12m D.14m
6.如图,为了测量某棵树的高度,小明用长为2m的竹竿作测量工具,移动竹竿,使竹竿顶端、树的顶端的影子恰好落在地面的同一点.此时竹竿与这一点相距6m,与树相距15m,则树的高度为( )
A.4m B.5m C.7m D.9m
7.(2020九上·慈溪月考)小明在测量楼高时,先测出楼房落在地面上的影长BA为15米,如图所示,然后在A处树立一根高2米的标杆,测得标杆的影长AC为3米,则楼高为( )
A.10米 B.12米 C.15米 D.22.5米
8.(2024九上·开封期末)如图,在小孔成像的实验中,蜡烛与有小孔的纸板之间的水平距离为.当蜡烛火焰的高度是它的像高度的一半时,有小孔的纸板与光屏之间的水平距离为( )
A. B. C. D.
9.如图所示,一张等腰三角形纸片,底边长18cm,底边上的高长18cm,现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条,已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
A.第4张 B.第5张 C.第6张 D.第7张
10.(2022九上·榆树期中)如图 ABCD,F为BC中点,延长AD至E,使 ,连结EF交DC于点G,则 =( )
A.2:3 B.3:2 C.9:4 D.4:9
二、填空题
11.(2024九上·浙江期末)如图是一位同学用激光笔测量某古城墙高度的示意图.点处放一水平的平面镜,光线从点出发经平面镜反射后刚好到古城墙的顶端处,若,,测得,,,则该古城墙的高度是 .
12.(2024九下·青山湖模拟)如图,已知零件的外径为,要求它的厚度,需先求出内孔的直径,现用一个交叉卡钳(两条尺长和相等)去量,若,且量得,则厚度 .
13.(2024七上·邵阳月考)如图所示,这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后,在地面上形成阴影(圆形)的示意图.已知桌面的直径为,桌面距离地面,若灯泡距离地面,则地面上阴影部分的面积为 .
14.(2022九下·普陀期中)如图,中,E是边AD的中点,BE交对角线AC于点F,那么S△AFB :S四边形FEDC的值为
15.(2023九上·萧山期中)甲、乙两同学测量一棵树的高度,在阳光下,甲同学测得一根1米长的竹竿的影长为0.8米,同时,乙同学测量时,发现树的影子不全落在地面上,如图,有一部分影子落在教学楼的墙壁上,其影长CD=1.2米,落在地面上的影长BC=2.4米,则树高AB的长是 米.
16.(2022·番禺模拟)如图,将 ABCD绕点A逆时针旋转到 AB′C′D′的位置,使点B′落在BC上,B′C′与CD交于点E.若AB=3,BC=4,BB′=1,则CE的长为 .
三、计算题
17.(2023九上·法库期中)某“综合与实践”小组开展了测量本校旗杆高度的实践活动,如图,他们在旗杆底部所在的平地上放置一个平面镜E来测量学校旗杆的高度,镜子中心E与旗杆的距离米,当镜子中心E与测量者的距离米时,测量者刚好从镜子中看到旗杆顶部的端点A.已知测量者的身高为1.6米,测量者的眼睛距地面的高度为1.5米.
(1)在计算过程中C、D之间的距离应是______米;
(2)根据以上测量结果,求出学校旗杆的高度.
18.(2024八下·苏州工业园月考)为了加快城市发展,保障市民出行方便,某市在流经该市的河流上架起一座桥,连通南北,铺就城市繁荣之路.小明和小颖想通过自己所学的数学知识计算该桥AF的长.如图,该桥两侧河岸平行,他们在河的对岸选定一个目标作为点A,再在河岸的这一边选出点B和点C,分别在AB、AC的延长线上取点D、E,使得DEBC.经测量,BC=120米,DE=210米,且点E到河岸BC的距离为60米.已知AF⊥BC于点F,请你根据提供的数据,帮助他们计算桥AF的长度.
四、解答题
19.(2024九下·石嘴山月考)如图,路灯(点)距地面8米,身高1.6米的小明从距路灯的底部(点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?
20.(2023九上·金台期中)如图①,“丝绸之路群雕”刻画和表达了一队来往于丝路中途的中外混合的骆驼商旅,已成为西安著名的城市标志之一.为了测量群雕某处的高度,小明和晓璐带着平面镜和皮尺去进行测量.测量过程如下:如图②,首先,小明在处放置了一面平面镜,然后沿后退,当小明蹲在点处时恰好能在平面镜中看到雕塑顶端的像,此时小明的眼睛到地面的距离米,米;然后小明在处起立站直,晓璐眼睛贴地观察发现地面上点、小明头顶和顶端重合,测得小明的身高米,米,,,点、、、在同一条水平线上,点在上,请你求出该处雕塑的高.(平面镜的大小、厚度忽略不计,晓璐眼睛贴地观察时眼睛到地面的距离忽略不计)
21.(2017·西安模拟)某学校的学生为了对小雁塔有基本的认识,在老师的带领下对小雁塔进行了测量.测量方法如下:如图,间接测得小雁塔地部点D到地面上一点E的距离为115.2米,小雁塔的顶端为点B,且BD⊥DE,在点E处竖直放一个木棒,其顶端为C,CE=1.72米,在DE的延长线上找一点A,使A、C、B三点在同一直线上,测得AE=4.8米.求小雁塔的高度.
22.(2023九上·黄岛期中)已知不等臂跷跷板的长为3米,当的一端点碰到地面时(如图1),点离地高1.5米;当的另一端点碰到地面时(如图2),点离地高1米,求跷跷板的支撑点到地面的距离。
答案解析部分
1.【答案】A
【知识点】相似三角形的性质;相似三角形的应用
2.【答案】B
【知识点】相似三角形的应用
3.【答案】B
【知识点】相似三角形的应用
4.【答案】A
【知识点】相似三角形的应用
5.【答案】B
【知识点】相似三角形的应用
6.【答案】C
【知识点】相似三角形的应用
7.【答案】A
【知识点】相似三角形的应用
8.【答案】C
【知识点】相似三角形的应用
9.【答案】B
【知识点】相似三角形的应用
10.【答案】D
【知识点】相似三角形的判定与性质;相似三角形的应用
11.【答案】4.5
【知识点】相似三角形的应用
12.【答案】2
【知识点】相似三角形的应用
13.【答案】
【知识点】相似三角形的应用
14.【答案】
【知识点】三角形的面积;两条直线被一组平行线所截,所得的对应线段成比例;相似三角形的应用
15.【答案】4.2
【知识点】相似三角形的应用
16.【答案】
【知识点】三角形的面积;勾股定理的应用;相似三角形的应用
17.【答案】(1)1.5
(2)15米
【知识点】相似三角形的判定;相似三角形的应用
18.【答案】桥AF的长度为80米.
【知识点】相似三角形的应用
19.【答案】从点走到点,身影的长度是变短了
【知识点】相似三角形的应用
20.【答案】该处雕塑的高为7米.
【知识点】相似三角形的应用
21.【答案】解:由题意可得:△AEC∽△ADB,
则 = ,
故 = ,
解得:DB=43,
答:小雁塔的高度为43m
【知识点】相似三角形的应用
22.【答案】解:解:由题意可得,,,
∴,
在与中,
,
∴∴即∴
在与中,
,∴
∴即∴
∵∴∴
答:跷跷板的支撑点到地面的距离为0.6米.
【知识点】相似三角形的判定与性质;相似三角形的应用
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
