3.6 位似 同步练习（含答案）

中小学教育资源及组卷应用平台
3.6 位似
一、单选题
1．（2023九上·宁波期末）在平面直角坐标系中，已知点E（3，﹣6），F（﹣6，9），以原点O为位似中心，把△EOF缩小为原来的 ，则点F的对应点F′的坐标是（　　）
A．（1，﹣2） B．（﹣2，3）
C．（1，﹣2）或（﹣1，2） D．（﹣2，3）或（2，﹣3）
2．（2018九上·新野期中）如图，在平面直角坐标系中，已知点A（-3，6）、B（-9，-3），以原点O为位似中心，相似比为 ，把△ABO缩小，则点A的对应点A′的坐标是（　　）
A． B．
C． 或 D． 或
3．（2023·衡阳模拟） 位似于 ，它们的周长比为 ，已知位似中心O到A的距离为3，那么O到D的距离为（　　）
A．4 B．4.5 C．6 D．9
4．（2021九上·沈河期末）在平面直角坐标系中，点A，B的坐标分别是（4，2），B（5，0），以O为位似中心，相似比为 ，把△ABO缩小，得到△A1B1O，则点A的对应点A1的坐标为（　　）
A．（2，1） B．（2，﹣1）
C．（﹣2，﹣1） D．（2，1）或（﹣2，﹣1）
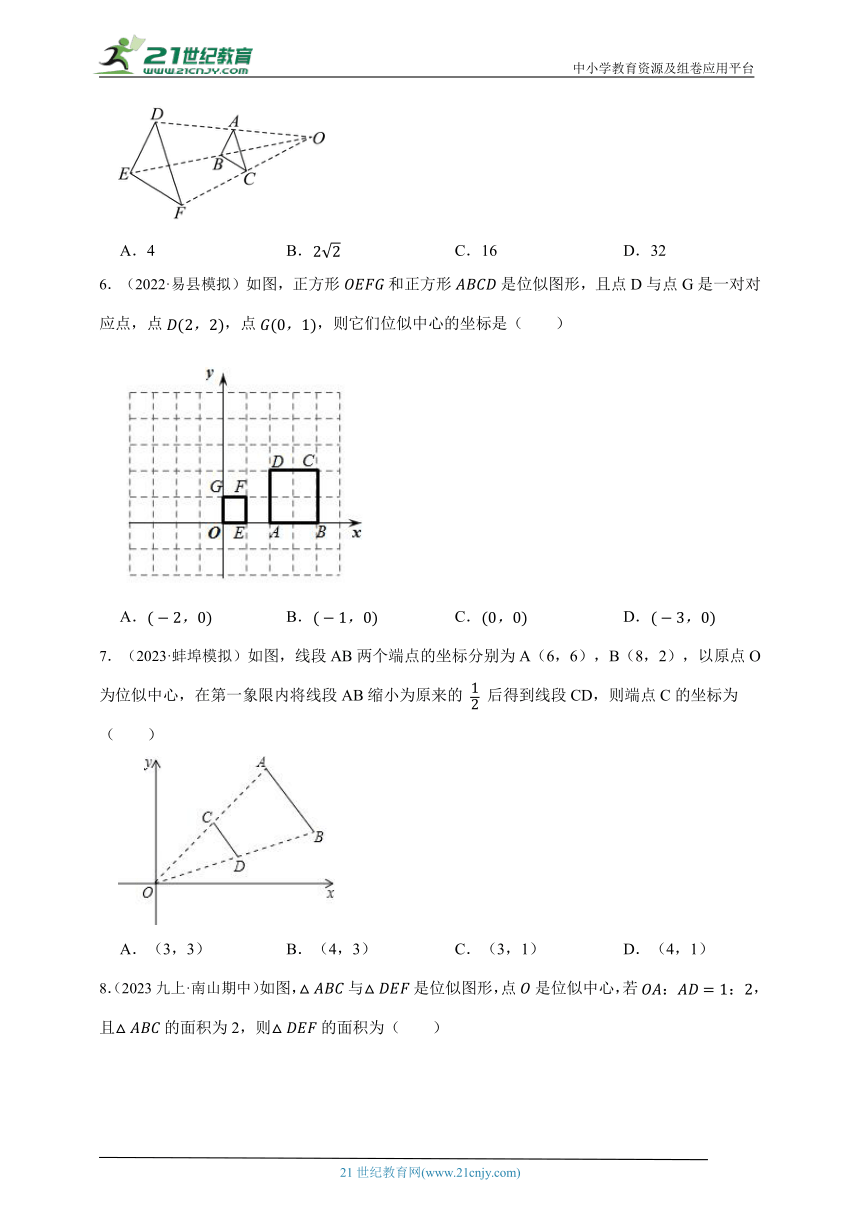
5．（2024·天山模拟） 如图，与是位似图形，点O为位似中心，且，若的周长为8，则的周长为（　　）
A．4 B． C．16 D．32
6．（2022·易县模拟）如图，正方形和正方形是位似图形，且点D与点G是一对对应点，点，点，则它们位似中心的坐标是（　　）
A． B． C． D．
7．（2023·蚌埠模拟）如图，线段AB两个端点的坐标分别为A（6，6），B（8，2），以原点O为位似中心，在第一象限内将线段AB缩小为原来的 后得到线段CD，则端点C的坐标为（　　）
A．（3，3） B．（4，3） C．（3，1） D．（4，1）
8．（2023九上·南山期中）如图，与是位似图形，点是位似中心，若，且的面积为2，则的面积为（　　）
A．6 B．9 C．18 D．27
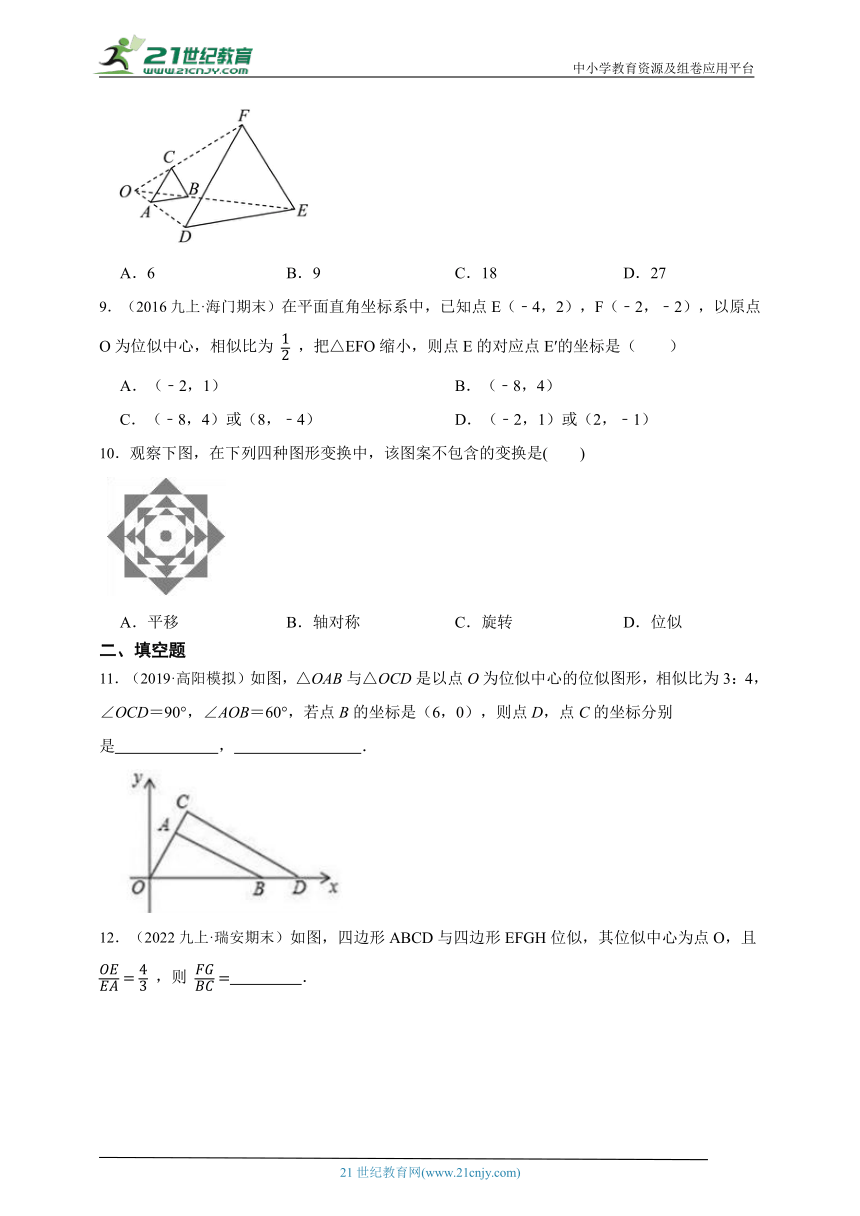
9．（2016九上·海门期末）在平面直角坐标系中，已知点E（﹣4，2），F（﹣2，﹣2），以原点O为位似中心，相似比为 ，把△EFO缩小，则点E的对应点E′的坐标是（　　）
A．（﹣2，1） B．（﹣8，4）
C．（﹣8，4）或（8，﹣4） D．（﹣2，1）或（2，﹣1）
10．观察下图，在下列四种图形变换中，该图案不包含的变换是(　　)
A．平移 B．轴对称 C．旋转 D．位似
二、填空题
11．（2019·高阳模拟）如图，△OAB与△OCD是以点O为位似中心的位似图形，相似比为3：4，∠OCD＝90°，∠AOB＝60°，若点B的坐标是（6，0），则点D，点C的坐标分别是　 　，　 　．
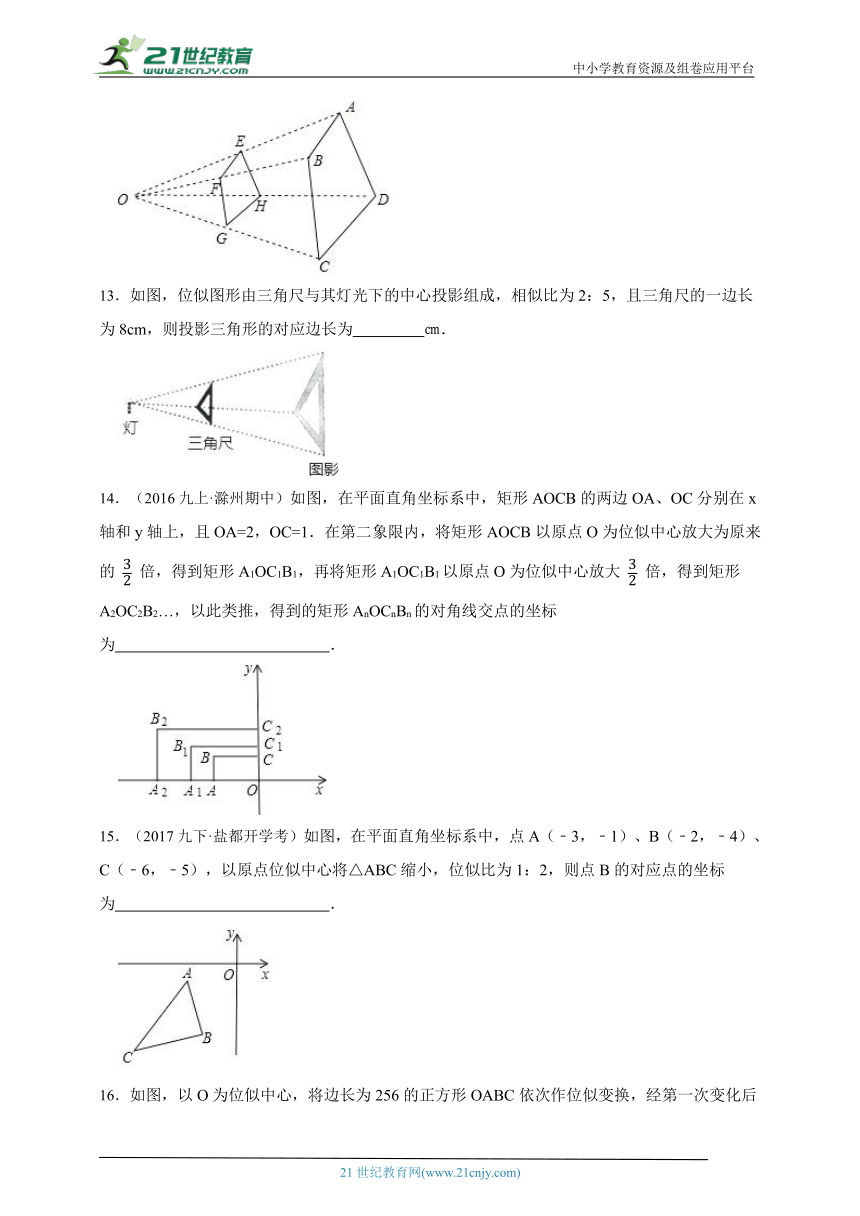
12．（2022九上·瑞安期末）如图，四边形ABCD与四边形EFGH位似，其位似中心为点O，且 ，则 　 　．
13．如图，位似图形由三角尺与其灯光下的中心投影组成，相似比为2：5，且三角尺的一边长为8cm，则投影三角形的对应边长为　 　㎝．
14．（2016九上·滁州期中）如图，在平面直角坐标系中，矩形AOCB的两边OA、OC分别在x轴和y轴上，且OA=2，OC=1．在第二象限内，将矩形AOCB以原点O为位似中心放大为原来的 倍，得到矩形A1OC1B1，再将矩形A1OC1B1以原点O为位似中心放大 倍，得到矩形A2OC2B2…，以此类推，得到的矩形AnOCnBn的对角线交点的坐标为　 　．
15．（2017九下·盐都开学考）如图，在平面直角坐标系中，点A（﹣3，﹣1）、B（﹣2，﹣4）、C（﹣6，﹣5），以原点位似中心将△ABC缩小，位似比为1：2，则点B的对应点的坐标为　 　．
16．如图，以O为位似中心，将边长为256的正方形OABC依次作位似变换，经第一次变化后得正方形OA1B1C1，其边长OA1缩小为OA的，经第二次变化后得正方形OA2B2C2，其边长OA2缩小为OA1的，经第，三次变化后得正方形OA3B3C3，其边长OA3缩小为OA2的，…，依次规律，经第n次变化后，所得正方形OAnBnCn的边长为正方形OABC边长的倒数，则n= 　 　．
三、解答题
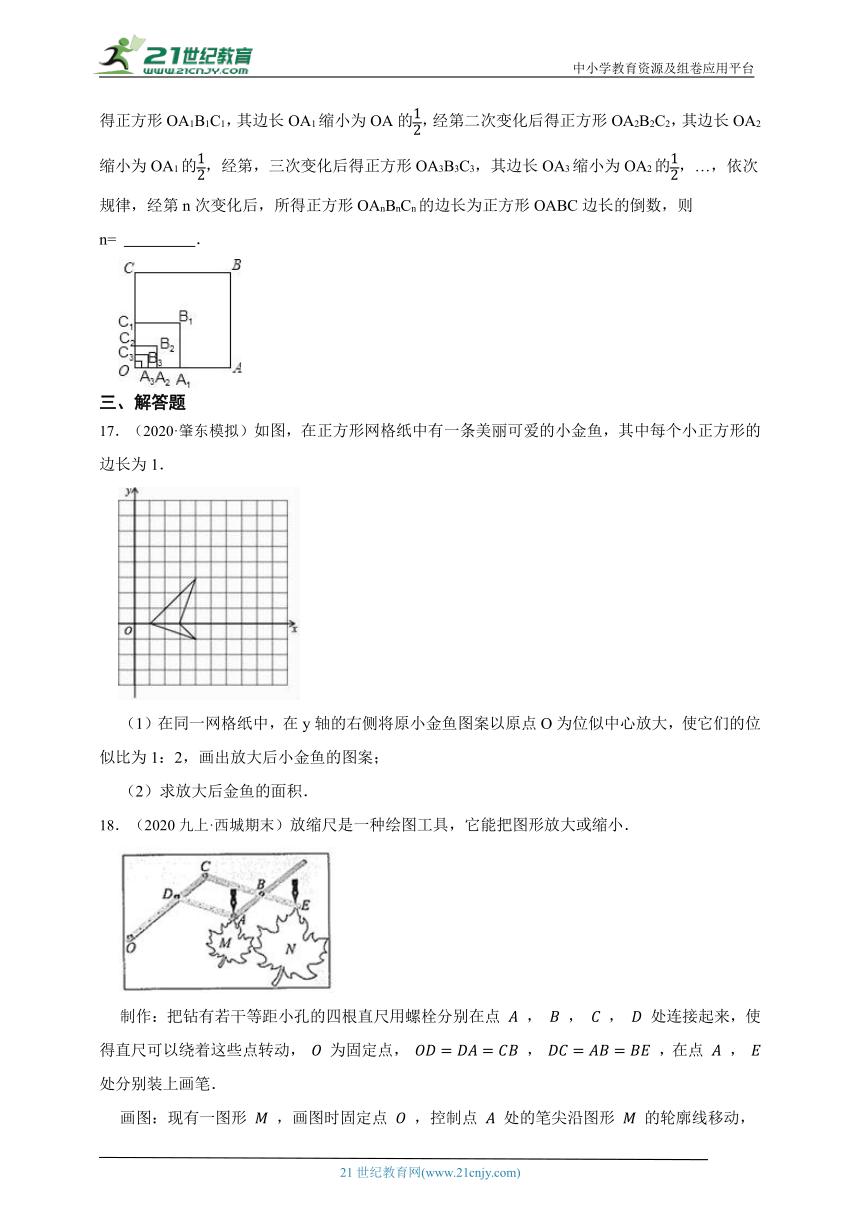
17．（2020·肇东模拟）如图，在正方形网格纸中有一条美丽可爱的小金鱼，其中每个小正方形的边长为1．
（1）在同一网格纸中，在y轴的右侧将原小金鱼图案以原点O为位似中心放大，使它们的位似比为1：2，画出放大后小金鱼的图案；
（2）求放大后金鱼的面积．
18．（2020九上·西城期末）放缩尺是一种绘图工具，它能把图形放大或缩小．
制作：把钻有若干等距小孔的四根直尺用螺栓分别在点 ， ， ， 处连接起来，使得直尺可以绕着这些点转动， 为固定点， ， ，在点 ， 处分别装上画笔．
画图：现有一图形 ，画图时固定点 ，控制点 处的笔尖沿图形 的轮廓线移动，此时点 处的画笔便画出了将图形 放大后的图形 ．
原理：
连接 ， ，可证得以下结论：
① 和 为等腰三角形，则 ， （180°-∠ ▲ ）；
②四边形 为平行四边形（理由是 ▲ ）；
③ ，于是可得 ， ， 三点在一条直线上；
④当 时，图形 是以点 为位似中心，把图形 放大为原来的 ▲ 倍得到的．
答案解析部分
1．【答案】D
【知识点】位似变换
2．【答案】B
【知识点】位似变换
3．【答案】B
【知识点】位似变换
4．【答案】D
【知识点】位似变换
5．【答案】C
【知识点】位似变换
6．【答案】A
【知识点】位似变换
7．【答案】A
【知识点】坐标与图形性质；位似变换
8．【答案】C
【知识点】相似三角形的判定与性质；位似变换
9．【答案】D
【知识点】坐标与图形性质；位似变换
10．【答案】A
【知识点】轴对称图形；位似变换；图形的旋转
11．【答案】（8，0）；（2，2 ）
【知识点】位似变换
12．【答案】
【知识点】位似变换
13．【答案】20cm
【知识点】位似变换
14．【答案】（﹣ ， ）
【知识点】坐标与图形性质；矩形的性质；位似变换
15．【答案】（﹣1，﹣2）或（1，2）
【知识点】坐标与图形性质；位似变换
16．【答案】16
【知识点】正方形的性质；位似变换
17．【答案】（1）解：如图所示：
（2）解：S金鱼= ×4×（6+2）=16
【知识点】作图﹣相似变换；位似变换；作图﹣位似变换
18．【答案】解：连接 ， ，如图，
①∵ ，
∴
∴△OAD和△OEC是等腰三角形，
∴∠ ，∠
∴∠ ，∠
②∵ ，
∴四边形 为平行四边形（两组对边分别相等的四边形是平行四边形）
③∵
∴ ， ， 三点在一条直线上；
④∵图形M和图形N是以点O为位似中心的位似图形，
∴其倍数比为三角形的边长比即： ，
又 ，且
∴
即：当 时，图形 是以点 为位似中心，把图形 放大为原来的 倍得到的．
故答案为： ；两组对边分别相等的四边形是平行四边形；
【知识点】位似变换
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
21世纪教育网(www.21cnjy.com)