2026年中考数学复习课件 专题六 圆--第27讲 与圆有关的计算(共45张PPT)
文档属性
| 名称 | 2026年中考数学复习课件 专题六 圆--第27讲 与圆有关的计算(共45张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 21:33:50 | ||
图片预览











文档简介
(共45张PPT)
复习讲义
第一篇 考点精讲
专题六 圆
第27讲 与圆有关的计算
聚焦核心
1.圆中的计算
图形 计算
__________________________ 的周长 _____
的面积 _____
_______________________________ 弧长 _ ___
扇形的面积 _ ____,
或 _ ___
2.圆柱、圆锥的侧面展开图及有关计算
图形 侧面展开图 有关计算
_____________________________ 圆柱 圆柱的侧面展 开图是____形 若为底面半径, 为圆柱的高,则
______;
_____________
________________________ 圆锥 圆锥的侧面展 开图是____形 若为底面半径,为母线长, 为圆锥的
高,则
____;
__________
矩
扇
3.圆的内接正 边形
图形 多边形为的内接正 边形,
设其半径为,边心距为,边长为,中
心角为
中心角 _ ____
边长
边心距
第27讲 与圆有关的计算
案例分析
考点一 弧长的有关计算
名师指导
1.利用弧长公式
的度数和半径.
2.从弧长公式可以看出,弧长
只要知道其中任意两个量,即可求出第三个量.
例1 (2024·安徽·中考)若扇形的半径为6, ,则
的长为( ).
A. B. C. D.
提示: .
C
思路点拨 利用弧长公式直接代入计算即可,其中 ,
.
考点专练
1.(2025·黑龙江哈尔滨·中考模拟)一个扇形的圆心角是 ,弧长是 ,
则这个扇形的半径是___ .
3
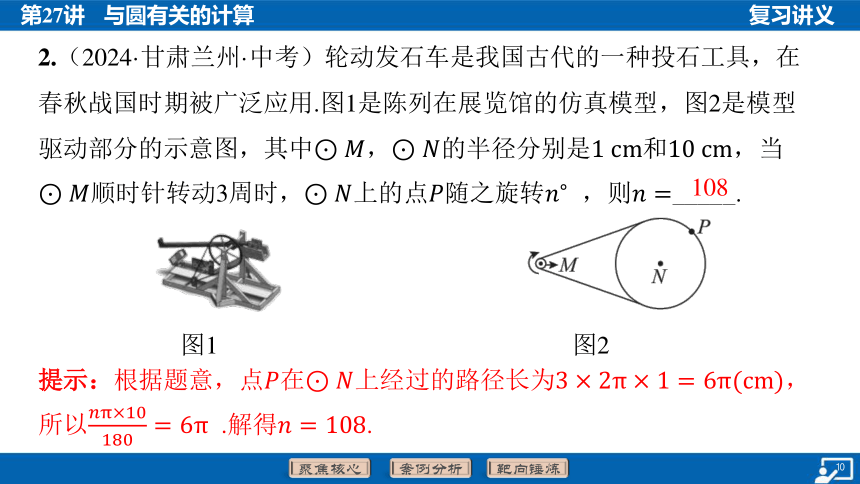
2.(2024·甘肃兰州·中考)轮动发石车是我国古代的一种投石工具,在
春秋战国时期被广泛应用.图1是陈列在展览馆的仿真模型,图2是模型
驱动部分的示意图,其中,的半径分别是和 ,当
顺时针转动3周时,上的点随之旋转 ,则 _____.
图1
图2
108
提示:根据题意,点在上经过的路径长为 ,
所以 .解得 .
考点二 扇形面积的有关计算
名师指导
根据已知条件,灵活选择公式计算扇形面积:
(1)当已知半径
(2)当已知半径
图3
例2 传统文化(2024·山东东营·中考)中华优秀传统文
化是中华民族的“根”和“魂”.东营市某学校组织开展中华
优秀传统文化成果展示活动,小慧同学制作了一把扇形
纸扇.如图3,, ,纸扇完全打开
A. B. C. D.
后,外侧两条竹片(竹片宽度忽略不计)的夹角 .现需在
扇面一侧绘制山水画,则山水画所在纸面的面积为( ).
思路点拨 纸面的面积 ,两个扇形的半径和圆心角都
已知,直接利用面积公式 即可求出它们的面积.
图3
提示:纸面的面积为.
答案:C
考点专练
3.一个扇形的弧长为 ,半径长为4,则该扇形的面积为( ).
C
A. B. C. D.
4.(2025·湖南永州·中考模拟)已知扇形的半径为6,面积为 ,则扇形圆
心角的度数为____.
图4
5.(2025·广西玉林·中考模拟)数学课上,
老师将图4中边长为1的正方形铁丝框
变形成以点为圆心, 长为半径的
扇形(铁丝的粗细忽略不计),则所
得扇形 的面积是___.
1
考点三 圆锥的有关计算
名师指导
1.在圆锥中,底面半径、高和母线构成直角三角形,于是可利用勾
股定理解决问题.
2.在解决与圆锥有关的计算时,要抓住两个对应关系:
(1)圆锥的母线长等于圆锥侧面展开形成的扇形的半径;
(2)圆锥的底面圆周长等于圆锥侧面展开形成的扇形的弧长.
例3 (2024·江苏无锡·中考)已知圆锥的底面圆半径为3,母线长为4,
则圆锥的侧面积为( ).
A. B. C. D.
提示:由题意,可知圆锥的侧面展开形成的扇形的弧长, 扇形的半径为4,因此圆锥的侧面积= .
思路点拨 圆锥的侧面展开图是扇形,扇形的弧长等于圆锥底面圆的周
长,扇形的半径是圆锥的母线长,利用面积公式 即可求出圆
锥的侧面积.
B
考点专练
6.(2024·江苏宿迁·中考)已知圆锥的底面圆半径为3,母线长为12,则
其侧面展开扇形的圆心角的度数为____.
提示:设侧面展开扇形的圆心角的度数为 ,则侧面展开扇形的弧长
为.解得 .
7.(2024·黑龙江绥化·中考)用一个圆心角为 ,半径为 的扇
形作一个圆锥的侧面,这个圆锥的底面圆的半径为__ .
提示:设这个圆锥的底面圆的半径为.由题意,得 .解
得 .
8.(2024·黑龙江齐齐哈尔·中考)若圆锥的底面圆半径是 ,它的侧
面展开图的圆心角是直角,则该圆锥的高为_____ .
提示:设圆锥的母线长为.根据题意,得.解得 ,即
圆锥的母线长为.所以圆锥的高 .
考点四 正多边形和圆的有关计算
名师指导
1.正多边形中有关角的计算公式:
(1)正
(2)正
2.正多边形中有关边的计算公式:(设正多边形的边心距为 ,半
径为,边长为,边数为,周长为,面积为 )
(1) ;
(2) ;
(3) .
图5
例4 (2024·山东济宁·中考)如图5,边长为2的正六边
形内接于 ,则它的内切圆半径为( ).
A.1 B.2 C. D.
思路点拨 过点作于点,则 即为正六
边形内切圆的半径.连接, ,构造特殊
三角形,结合正多边形、三角形的性质可求得 的长.
图5
图48
提示:如图48,连接,,过点作 ,垂
足为点.因为六边形是正六边形,点 是它
的中心,所以 .又因为 ,
所以是等边三角形.所以 ,
.所以 ,即正六边
形的内切圆半径为 .
答案:D
考点专练
图6
9.(2025·蚌埠·中考改编)如图6,正五边形 内接于
,连接,,则 的度数为
( ).
D
A. B. C. D.
图7
10.数学文化(2024·山东东营·中考)我国魏晋时期数学家
刘徽在《九章算术注》中提到著名的“割圆术”,即利用圆
的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,
所失弥少.割之又割,以至于不可割,则与圆周合体,而无
所失矣.”“割圆术”孕育了微积分思想,他用这种思想得到了圆周率 的近似值为.如图7, 的半径为1,运用 “割圆术”,以圆内接正六边形面积近似估计 的面积,可得 的估计值为.若用圆内接正八边形近似估计 的面积,可得 的估计值为_____.(结果保留根号)
图49
提示:如图49,正八边形内接于 ,连
接,,过点作于点 .因为八边形
是正八边形,所以 .在
中,, ,所以
.所以正八边形的面积为
.由此可估计 的近似
值为 .
第27讲 与圆有关的计算
靶向锤炼
靶向练
图1
1.(2024·贵州·中考)如图1,在扇形纸扇中,若
,,则 的长为( ).
C
A. B. C. D.
图2
2.(2025·新疆·中考模拟)如图2,在 中,若
,,则扇形 (阴影部分)的面积
是( ).
B
A. B. C. D.
3.(2024·云南·中考)某校九年级学生参加社会实践,学习编织圆锥形
工艺品.若这种圆锥的母线长为,底面圆的半径为 ,则该圆
锥的侧面积为( ).
C
A. B. C. D.
图3
4.(2024·四川雅安·中考)如图3,的周长为 ,
正六边形内接于, 的面积为( ).
B
A.4 B. C.6 D.
5.(2024·湖南长沙·中考)半径为4,圆心角为 的扇形的面积为____.
(结果保留 )
图4
6.(2024·吉林长春·中考)一块含 角的直角三
角尺按如图4所示的方式摆放,边与直线
重合,.现将该三角尺绕点 顺时针旋
转,使点的对应点落在直线上,则点 经过的
路径长至少为____.(结果保留 )
图4
提示:由旋转的性质,得 ,
即 .故点 经过的路径长至少为
.
图5
7.(2024·江苏宿迁·中考)如图5,已知正六边形
的边长为2,以点为圆心, 长为半径作圆,
则该圆被正六边形截得的的长为___.(结果保留 )
图6
8.(2024·内蒙古通辽·中考)如图6,为便于研究圆锥与扇形
的关系,小方同学利用扇形纸片恰好围成一个底面半径为
,母线长为 的圆锥的侧面,那么这个扇形纸片的面
积是_____.(结果保留 )
9.(2025·江苏扬州·中考改编)若用半径为 的半圆形纸片围成一个圆锥
的侧面,则这个圆锥底面圆的半径为___ .
10.(2024·大庆·中考改编)若圆锥的底面半径为3,侧面积为 ,则这
个圆锥侧面展开图的圆心角是____ .
5
90
攻坚练
图7
11.(2024·河南·中考)如图7,是边长为 的等边
三角形的外接圆,点是的中点,连接, .以
点为圆心,的长为半径在 内画弧,则阴影部分
的面积为( ).
A. B. C. D.
图71
提示:如图71,过点D作于点.因为 是边长
为的等边三角形的外接圆,所以 ,
, .所以 .因
为点D是的中点,所以,即 .所以
, .从而得
.故 .
【答案】C
图8
12.(2025·广西北部湾经济区·中考模拟)如图8,在
中,, .将绕点 逆时针
旋转 ,得到,连接并延长交于点 .
当时, 的长为( ).
A. B. C. D.
图8
提示:因为, ,所以
.由旋转的性质,得 .所以
.在中, ,所
以. 从而得
.所以 .在
【答案】B
中, ,所以
.故的长为 .
13.(2024·甘肃临夏·中考)如图9,对折边长为2的正方形纸片 ,
为折痕,以点为圆心,的长为半径作弧,分别交, 于点
,,则的长为___.(结果保留 )
图9
图72
提示:由折叠的性质,得四边形 是矩形,
.所以, .如
图72,过点作于点,则 .因为
,,所以 .从而得
.故的长为 .
拔尖练
14.(2024·广东·中考)综合与实践
【主题】滤纸与漏斗
【材料】如图10所示:
图10
①一张直径为 的圆形滤纸;
②一只漏斗口直径与母线均为 的圆锥形过滤漏斗.
【实践操作】
步骤1:取一张滤纸.
步骤2:按如图11所示步骤折叠好滤纸.
图11
步骤3:将其中一层撑开,围成圆锥形滤纸.
步骤4:将围成圆锥形滤纸放入如图10所示漏斗中.
【实践探索】
(1)滤纸是否能紧贴此漏斗内壁(忽略漏斗管口处)?用你所学的数
学知识说明.
解:滤纸能紧贴此漏斗内壁.
理由:设圆锥形过滤漏斗的侧面展开图的扇形圆心角为.
根据题意,得 .
解得 .
由题意可知,围成圆锥形滤纸的侧面展开图的扇形圆心角度数为 .
滤纸能紧贴此漏斗内壁.
(2)当滤纸紧贴漏斗内壁时,求滤纸围成的圆锥的体积.(结果保留 )
解:设滤纸围成的圆锥底面圆的半径为,高为 .
根据题意,得.
解得.
圆锥的体积为 .
复习讲义
第一篇 考点精讲
专题六 圆
第27讲 与圆有关的计算
聚焦核心
1.圆中的计算
图形 计算
__________________________ 的周长 _____
的面积 _____
_______________________________ 弧长 _ ___
扇形的面积 _ ____,
或 _ ___
2.圆柱、圆锥的侧面展开图及有关计算
图形 侧面展开图 有关计算
_____________________________ 圆柱 圆柱的侧面展 开图是____形 若为底面半径, 为圆柱的高,则
______;
_____________
________________________ 圆锥 圆锥的侧面展 开图是____形 若为底面半径,为母线长, 为圆锥的
高,则
____;
__________
矩
扇
3.圆的内接正 边形
图形 多边形为的内接正 边形,
设其半径为,边心距为,边长为,中
心角为
中心角 _ ____
边长
边心距
第27讲 与圆有关的计算
案例分析
考点一 弧长的有关计算
名师指导
1.利用弧长公式
的度数和半径.
2.从弧长公式可以看出,弧长
只要知道其中任意两个量,即可求出第三个量.
例1 (2024·安徽·中考)若扇形的半径为6, ,则
的长为( ).
A. B. C. D.
提示: .
C
思路点拨 利用弧长公式直接代入计算即可,其中 ,
.
考点专练
1.(2025·黑龙江哈尔滨·中考模拟)一个扇形的圆心角是 ,弧长是 ,
则这个扇形的半径是___ .
3
2.(2024·甘肃兰州·中考)轮动发石车是我国古代的一种投石工具,在
春秋战国时期被广泛应用.图1是陈列在展览馆的仿真模型,图2是模型
驱动部分的示意图,其中,的半径分别是和 ,当
顺时针转动3周时,上的点随之旋转 ,则 _____.
图1
图2
108
提示:根据题意,点在上经过的路径长为 ,
所以 .解得 .
考点二 扇形面积的有关计算
名师指导
根据已知条件,灵活选择公式计算扇形面积:
(1)当已知半径
(2)当已知半径
图3
例2 传统文化(2024·山东东营·中考)中华优秀传统文
化是中华民族的“根”和“魂”.东营市某学校组织开展中华
优秀传统文化成果展示活动,小慧同学制作了一把扇形
纸扇.如图3,, ,纸扇完全打开
A. B. C. D.
后,外侧两条竹片(竹片宽度忽略不计)的夹角 .现需在
扇面一侧绘制山水画,则山水画所在纸面的面积为( ).
思路点拨 纸面的面积 ,两个扇形的半径和圆心角都
已知,直接利用面积公式 即可求出它们的面积.
图3
提示:纸面的面积为.
答案:C
考点专练
3.一个扇形的弧长为 ,半径长为4,则该扇形的面积为( ).
C
A. B. C. D.
4.(2025·湖南永州·中考模拟)已知扇形的半径为6,面积为 ,则扇形圆
心角的度数为____.
图4
5.(2025·广西玉林·中考模拟)数学课上,
老师将图4中边长为1的正方形铁丝框
变形成以点为圆心, 长为半径的
扇形(铁丝的粗细忽略不计),则所
得扇形 的面积是___.
1
考点三 圆锥的有关计算
名师指导
1.在圆锥中,底面半径、高和母线构成直角三角形,于是可利用勾
股定理解决问题.
2.在解决与圆锥有关的计算时,要抓住两个对应关系:
(1)圆锥的母线长等于圆锥侧面展开形成的扇形的半径;
(2)圆锥的底面圆周长等于圆锥侧面展开形成的扇形的弧长.
例3 (2024·江苏无锡·中考)已知圆锥的底面圆半径为3,母线长为4,
则圆锥的侧面积为( ).
A. B. C. D.
提示:由题意,可知圆锥的侧面展开形成的扇形的弧长, 扇形的半径为4,因此圆锥的侧面积= .
思路点拨 圆锥的侧面展开图是扇形,扇形的弧长等于圆锥底面圆的周
长,扇形的半径是圆锥的母线长,利用面积公式 即可求出圆
锥的侧面积.
B
考点专练
6.(2024·江苏宿迁·中考)已知圆锥的底面圆半径为3,母线长为12,则
其侧面展开扇形的圆心角的度数为____.
提示:设侧面展开扇形的圆心角的度数为 ,则侧面展开扇形的弧长
为.解得 .
7.(2024·黑龙江绥化·中考)用一个圆心角为 ,半径为 的扇
形作一个圆锥的侧面,这个圆锥的底面圆的半径为__ .
提示:设这个圆锥的底面圆的半径为.由题意,得 .解
得 .
8.(2024·黑龙江齐齐哈尔·中考)若圆锥的底面圆半径是 ,它的侧
面展开图的圆心角是直角,则该圆锥的高为_____ .
提示:设圆锥的母线长为.根据题意,得.解得 ,即
圆锥的母线长为.所以圆锥的高 .
考点四 正多边形和圆的有关计算
名师指导
1.正多边形中有关角的计算公式:
(1)正
(2)正
2.正多边形中有关边的计算公式:(设正多边形的边心距为 ,半
径为,边长为,边数为,周长为,面积为 )
(1) ;
(2) ;
(3) .
图5
例4 (2024·山东济宁·中考)如图5,边长为2的正六边
形内接于 ,则它的内切圆半径为( ).
A.1 B.2 C. D.
思路点拨 过点作于点,则 即为正六
边形内切圆的半径.连接, ,构造特殊
三角形,结合正多边形、三角形的性质可求得 的长.
图5
图48
提示:如图48,连接,,过点作 ,垂
足为点.因为六边形是正六边形,点 是它
的中心,所以 .又因为 ,
所以是等边三角形.所以 ,
.所以 ,即正六边
形的内切圆半径为 .
答案:D
考点专练
图6
9.(2025·蚌埠·中考改编)如图6,正五边形 内接于
,连接,,则 的度数为
( ).
D
A. B. C. D.
图7
10.数学文化(2024·山东东营·中考)我国魏晋时期数学家
刘徽在《九章算术注》中提到著名的“割圆术”,即利用圆
的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,
所失弥少.割之又割,以至于不可割,则与圆周合体,而无
所失矣.”“割圆术”孕育了微积分思想,他用这种思想得到了圆周率 的近似值为.如图7, 的半径为1,运用 “割圆术”,以圆内接正六边形面积近似估计 的面积,可得 的估计值为.若用圆内接正八边形近似估计 的面积,可得 的估计值为_____.(结果保留根号)
图49
提示:如图49,正八边形内接于 ,连
接,,过点作于点 .因为八边形
是正八边形,所以 .在
中,, ,所以
.所以正八边形的面积为
.由此可估计 的近似
值为 .
第27讲 与圆有关的计算
靶向锤炼
靶向练
图1
1.(2024·贵州·中考)如图1,在扇形纸扇中,若
,,则 的长为( ).
C
A. B. C. D.
图2
2.(2025·新疆·中考模拟)如图2,在 中,若
,,则扇形 (阴影部分)的面积
是( ).
B
A. B. C. D.
3.(2024·云南·中考)某校九年级学生参加社会实践,学习编织圆锥形
工艺品.若这种圆锥的母线长为,底面圆的半径为 ,则该圆
锥的侧面积为( ).
C
A. B. C. D.
图3
4.(2024·四川雅安·中考)如图3,的周长为 ,
正六边形内接于, 的面积为( ).
B
A.4 B. C.6 D.
5.(2024·湖南长沙·中考)半径为4,圆心角为 的扇形的面积为____.
(结果保留 )
图4
6.(2024·吉林长春·中考)一块含 角的直角三
角尺按如图4所示的方式摆放,边与直线
重合,.现将该三角尺绕点 顺时针旋
转,使点的对应点落在直线上,则点 经过的
路径长至少为____.(结果保留 )
图4
提示:由旋转的性质,得 ,
即 .故点 经过的路径长至少为
.
图5
7.(2024·江苏宿迁·中考)如图5,已知正六边形
的边长为2,以点为圆心, 长为半径作圆,
则该圆被正六边形截得的的长为___.(结果保留 )
图6
8.(2024·内蒙古通辽·中考)如图6,为便于研究圆锥与扇形
的关系,小方同学利用扇形纸片恰好围成一个底面半径为
,母线长为 的圆锥的侧面,那么这个扇形纸片的面
积是_____.(结果保留 )
9.(2025·江苏扬州·中考改编)若用半径为 的半圆形纸片围成一个圆锥
的侧面,则这个圆锥底面圆的半径为___ .
10.(2024·大庆·中考改编)若圆锥的底面半径为3,侧面积为 ,则这
个圆锥侧面展开图的圆心角是____ .
5
90
攻坚练
图7
11.(2024·河南·中考)如图7,是边长为 的等边
三角形的外接圆,点是的中点,连接, .以
点为圆心,的长为半径在 内画弧,则阴影部分
的面积为( ).
A. B. C. D.
图71
提示:如图71,过点D作于点.因为 是边长
为的等边三角形的外接圆,所以 ,
, .所以 .因
为点D是的中点,所以,即 .所以
, .从而得
.故 .
【答案】C
图8
12.(2025·广西北部湾经济区·中考模拟)如图8,在
中,, .将绕点 逆时针
旋转 ,得到,连接并延长交于点 .
当时, 的长为( ).
A. B. C. D.
图8
提示:因为, ,所以
.由旋转的性质,得 .所以
.在中, ,所
以. 从而得
.所以 .在
【答案】B
中, ,所以
.故的长为 .
13.(2024·甘肃临夏·中考)如图9,对折边长为2的正方形纸片 ,
为折痕,以点为圆心,的长为半径作弧,分别交, 于点
,,则的长为___.(结果保留 )
图9
图72
提示:由折叠的性质,得四边形 是矩形,
.所以, .如
图72,过点作于点,则 .因为
,,所以 .从而得
.故的长为 .
拔尖练
14.(2024·广东·中考)综合与实践
【主题】滤纸与漏斗
【材料】如图10所示:
图10
①一张直径为 的圆形滤纸;
②一只漏斗口直径与母线均为 的圆锥形过滤漏斗.
【实践操作】
步骤1:取一张滤纸.
步骤2:按如图11所示步骤折叠好滤纸.
图11
步骤3:将其中一层撑开,围成圆锥形滤纸.
步骤4:将围成圆锥形滤纸放入如图10所示漏斗中.
【实践探索】
(1)滤纸是否能紧贴此漏斗内壁(忽略漏斗管口处)?用你所学的数
学知识说明.
解:滤纸能紧贴此漏斗内壁.
理由:设圆锥形过滤漏斗的侧面展开图的扇形圆心角为.
根据题意,得 .
解得 .
由题意可知,围成圆锥形滤纸的侧面展开图的扇形圆心角度数为 .
滤纸能紧贴此漏斗内壁.
(2)当滤纸紧贴漏斗内壁时,求滤纸围成的圆锥的体积.(结果保留 )
解:设滤纸围成的圆锥底面圆的半径为,高为 .
根据题意,得.
解得.
圆锥的体积为 .
同课章节目录
