2026年中考数学复习课件 专题三 函数-第11讲 一次函数(共66张PPT)

(共66张PPT)
复习讲义
第一篇 吃透考点
专题三 函数
第11讲 一次函数
聚焦核心
1.一次函数和正比例函数的定义
（1）一次函数：一般地，形如_______，是常数，且 的函
数．
（2）正比例函数：一般地，形如____是常数，且 的函数．
2.一次函数的图象与正比例函数 的图象
的关系
（1）一次函数 的图象是一条______；特别地，正比
例函数 的图象是一条经过______的直线.
直线
原点
（2）一次函数 的图象可以由正比例函数
的图象平移得到.
①当时，的图象沿 轴向____平移___个单位长度，就得到
的图象;
②当时，的图象沿 轴向____平移____个单位长度，就得到
的图象.
上
下
（3）若直线与直线平行，则___ .
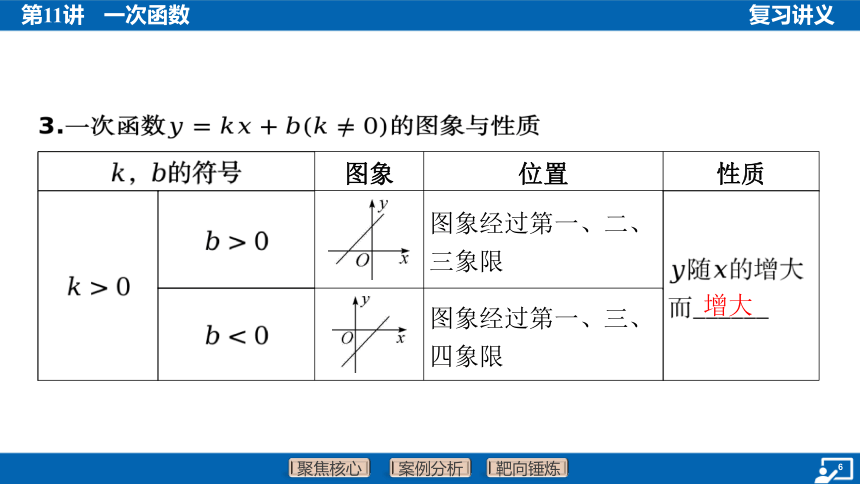
3.一次函数 的图象与性质
图象 位置 性质
______________________ 图象经过第一、二、 三象限
_____________________ 图象经过第一、三、 四象限 增大
图象 位置 性质
_______________________ 图象经过第一、二、 四象限
______________________ 图象经过第二、三、 四象限 减小
续表
4.一次函数与方程（组）、不等式的关系
（1）一次函数的图象与 轴交点的横坐标就是方程
___________的解．
（2）一次函数的图象在 轴上（或下）方部分的所有
点的横坐标就是不等式___0（或___ ）的解集．
（3）一般地，每个含有未知数和 的二元一次方程都可以转化成一次
函数，是常数，且 的形式，因此每个二元一次方程
都对应一个一次函数，也对应一条直线.这条直线上每个点的坐标
都是这个二元一次方程的____；以这个二元一次方程的每一对解为坐标
的点 ，都在这条直线上.
解
（4）从“形”的角度看，解二元一次方程组相当于确定两条相应直线
______的坐标.
交点
第11讲 一次函数
案例分析
考点一 一次函数的图象和性质
名师指导
1.在一次函数中：
（1）的值决定函数的增减性：当时，直线由左
至右上升，即随的增大而增大，一定经过第一、三象限；当时，
直线由左至右下降，即随的增大而减小，一定经过第二、
四象限.
（2）的值决定函数图象与轴的交点的位置：当 时，
直线交轴于正半轴，一定经过第一、二象限；当 时，
直线经过坐标原点；当时，直线交 轴于负
半轴，一定经过第三、四象限.
2.直线平移的规律：左右平移时，横坐标变化，左移加右移减；上
下平移时，纵坐标变化，上移加下移减.
（1）直线可以看作由直线 向 ___平移__________个单位长度而得到.
提示： （方法一）在中， ，所以直线可以看作由直线 向上平移2个单位长度而得到.（方法二）,所以直线 可以看作由直线 向右平移4个单位长度而得到.
例1 在平面直角坐标系中，已知直线 .
上
2（或右4）
思路点拨（1）利用一次函数图象的平移规律：“上加下减，左加右减” 进行解答.
（2）直线与轴的交点坐标为______，与 轴的交点坐标
为______.
提示：在中，当时，，解得 ，所以
直线与轴的交点坐标为.当时， ，所以直
线与轴的交点坐标为 .
思路点拨（2）函数图象与轴的交点的纵坐标为0，与 轴的交点的横坐标为0，据此即可求解.
（3）直线经过第____________象限，随 的增大而______.
一、二、四
减小
提示：在中，，又 ，所以直线
经过第一、二、四象限，随 的增大而减小.
思路点拨（3）根据一次函数解析式中系数的值，可以判断函数图象经过的象限和增减性.
（4）直线 与两坐标轴围成的三角形的面积是___.
4
图6
提示：直线 的大致图象如图6，设图象
与轴的交点为，与轴的交点为 .由（2）知，
，，所以， .所以
.
思路点拨（4）画出草图，可知该直线与坐标轴围成的三角形是直角三角形.将（2）中求出的交点坐标转化为直角三角形的直角边长，即可求解.
考点专练
图1
1.（2025·四川德阳·中考模拟）正比例函数 的
图象如图1所示，则 的值可能是( ).
A
A. B. C. D.
2.一次函数 的图象如图2所示，则下列结论正确的是( ).
B
图2
A. B.
C.随的增大而减小 D.当时，
3.（2025·甘肃临夏·中考模拟）一次函数的函数值随 的
增大而减小，它的图象不经过( ).
A
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4.（2025·广西南宁·模拟）直线向上平移5个单位长度后与 轴
的交点坐标是______.
5.（2025·广西北海·模拟）若，是直线 上
的两点，则___.（填“ ”“ ”或“ ”）
考点二 确定一次函数的解析式
名师指导
用待定系数法确定一次函数解析式的步骤：
（1）设：设一次函数解析式为（，是待定系数）.
（2）列：将已知点的坐标代入函数解析式，得到关于，的方程
（组）.
（3）解：解方程（组），求出，的值.
（4）代：将求得的和的值代入所设的函数解析式，进而写出一
次函数解析式．
图3
例2 （2024·浙江湖州·中考）如图3，与图中直线
关于 轴对称的直线的函数解析式是__________.
提示：因为直线与轴的交点为，与 轴的交点为，而所求直线与直线关于 轴对称，所以所求直线与轴的交点为，与轴的交点为 . 设所求直线的函数解析式为，将， 代入，得解得 因此所求直线的函数解析式为 .
思路点拨 两条直线关于轴对称，则它们与坐标轴的交点也关于 轴对称.只要求出直线与坐标轴的交点坐标，就可利用待定系数法求出直线的函数解析式.
考点专练
6.（2024·陕西·中考）一个正比例函数的图象经过点 和点
.若点与点 关于原点对称，则这个正比例函数的解析式为
( ).
A
A. B. C. D.
7.开放性题（2024·内蒙古包头·中考）在平面直角坐标系中，一次函数
的图象经过第一、二、三象限，请写出一个符合该条件的一次函数的解
析式：______________________________________________.
（答案不唯一，满足，均可）
图4
8.（2023·湖南益阳·中考）如图4，直线
与轴交于点，点关于 轴的对称
点为.设经过点和轴上的点 的直线
对应的函数解析式为 .
（1）求点 的坐标.
解：在中，令，则.所以
因为点 关于 轴的对称点为 ′，所以点的坐标为 .
（2）求直线 对应的函数解析式.
图4
解：将点，代入，得
解得
所以直线对应的函数解析式为 .
考点三 一次函数与方程（组）、不等式的关系
名师指导
1.直线与轴交点的横坐标就是关于的方程
的解．
2.直线在轴上方部分所有点的横坐标就是关于的不等
式0的解集；直线在轴下方部分所有点的横坐标就
是关于的不等式的解集.
3.直线与直线 的交点坐标就是方程组
的解.
图5
例3 一题多问如图5，直线 与直线
相交于点 .
（1）关于的方程的解为 ___.
2
提示：由图象知，直线经过点，即当 的
函数值为1时，对应的值为2，所以关于的方程的解为 .
思路点拨（1）该方程的解表示 3的函数值为1时对应的 值.
（2）关于的不等式 的解集为______.
图5
提示：由图象知，在点的右侧， 的函数值小于1，所以
关于的不等式的解集为 .
思路点拨（2）该不等式的解集表示 的函数值小于1时对应的 的取值范围.
图5
（3）关于，的方程组 的解为_______.
提示：由图象知，直线，相交于点 ，所以关
于，的方程组 的解为
思路点拨 （3）该方程组表示和 的函数值相等，故两个函数图象的交点的横坐标、纵坐标分别对应方程组解的 值、 值.
（4）关于的不等式 的解集为______.
图5
提示：由图象知，在交点的左侧，直线 在直线
的下方，所以关于的不等式 的解集为
.
思路点拨 （4）该不等式表示的函数值不大于 的函数值，故函数的图象在的下方部分（含交点）对应的 的取值范围即为该不等式的解集.
图5
（5）直线，与 轴围成的图形的面积是_ _.
提示：设直线与轴交于点 ，直线与轴交于点，则直线，与 轴围成的图形是.在中，当 时，，所以点的坐标为.在中，当时， ，所以点的坐标为.所以 .所以 .
思路点拨 （5）围成的图形为三角形.只要由两直线与 轴的交点坐标求出三角形的底边长，再将点 的横坐标转化为三角形的高，就可根据三角形的面积公式求解.
考点专练
9.（2024·广西柳州·模拟）正比例函数和一次函数
为常数，且的图象交于点，则关于 的不等式
的解集为( ).
D
A. B. C. D.
提示：将代入，得.将代入 ，得
.画出两条直线的图象（图略），可知当 时，直线
在直线的上方.所以当时， .
10.（2024·江苏扬州·中考）如图6，已知一次函数 的
图象分别与，轴交于点，，若，，则关于 的方程
的解为________.
图6
考点四 一次函数的应用
名师指导
应用一次函数知识解决实际问题常见的三种题型：
（1）先建立一次函数模型，然后借助方程、不等式或函数图象解
决方案选择问题；
（2）利用一次函数的图象和性质（如增减性）来解决生活优化问
题，它常与方程（组）或不等式知识一起考查；
（3）利用一次函数图象描述事物的变化规律问题，即分段函数问
题，解题时要注意各段函数的分界点.
例4 （2024·广西南宁·模拟） 1号探测气球从海拔 处出发，以
的速度上升，与此同时，2号探测气球从海拔 处出发，以
的速度上升，两个气球都上升了 后停止.
（1）分别求出表示两个气球所在位置的海拔关于上升时间
的函数解析式，并直接写出 的取值范围.
解：根据题意，得1号探测气球所在位置的海拔 ，2号探测气
球所在位置的海拔的取值范围为 .
思路点拨（1）气球上升的高度 气球上升的速度×上升的时间，而气球所在位置的海拔出发前的海拔 气球上升的高度.要注意单位的统一.
（2）两个气球能否在某个时刻位于同一高度 如果能，那么这时气球上
升了多长时间 位于什么高度
解：假设两个气球在某个时刻位于同一高度，则 .
解得 =20.
因为，所以符合题意.此时 .
答：两个气球能位于同一高度，此时气球上升了，都位于海拔 处.
思路点拨（2）当两个气球位于同一高度时， 值相等，可依此列出方程求解，注意检查方程的解是否在自变量的取值范围内.
考点专练
图7
11.数学文化（2025·甘肃武威·中考改编）“燕几”即宴几，是
世界上最早的一套组合桌，由北宋进士黄伯思设计.全套“燕
几”一共有七张桌子，包括两张长桌、两张中桌和三张小桌，
每张桌面的宽都相等.七张桌面可组合成不同的图形.图7给出
了《燕几图》中名称为“回文”的桌面拼合方式，若设每张桌
提示：由题图可得小桌的长为宽的2倍，则，即 .
面的宽为，长桌的长为，则与 的关系可以表示为_________.
图8
12.（2024·吉林·模拟）在日常生活中，当手
机剩余电量为 时，张老师便会给手机充电.他
发现单独用快充充电器和单独用普通充电器对该
手机充电，手机电量与充电时间 的
函数关系分别可用图8中的线段， 表示.请
根据图8中的信息，解答下列问题：
（1）张老师单独用快充充电器充满电比单独用普通充电器少用____ .
80
（2）求线段 对应的函数解析式.（不要求写出自变量的取值范围）
图8
解：设线段对应的函数解析式为，将 代入，得1.
解得.
故线段对应的函数解析式为 .
图8
（3）张老师先用普通充电器充电
后，再改用快充充电器将手机电量充满，
共用时，请求出 的值.
解：根据题意，得2 .
解得 .
第11讲 一次函数
靶向锤炼
靶向练
1.（2023·新疆·中考）一次函数 的图象不经过( ).
D
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.若一次函数的图象经过点，，则与 的大
小关系是( ).
B
A. B. C. D.
3.若一次函数 的图象如图1所示，则下列说法正确的是( ).
B
图1
A. B.
C.随的增大而增大 D.当时，
4.（2025·陕西延安·中考模拟）在同一平面直角坐标系中，函数 和
为常数， 的图象可能是( ).
D
A. B. C. D.
图2
5.（2024·广西钦州·模拟）如图2，直线
分别与轴，轴交于点，.将绕点 顺时针
旋转 得到，则点的对应点 的坐标是
( ).
C
A. B. C. D.
提示：由直线分别与轴，轴交于点A，B，得 ，
.所以，.所以 .
6.（2023·广西河池·模拟）已知部分鞋子的码数（单位：码）与鞋子长
度（单位： ）之间存在如下换算关系：
20 36 42
15 23 26
这种换算可以用一种函数关系去模拟，通过画图、观察、猜想，得
出与 之间的函数解析式为___________.
7.如图3，过点的直线 与直线
交于点 .
图3
（1）写出当时 的取值范围.
解：观察函数图象知，当时的取值范围是 .
图3
（2）求点的坐标和直线 的函数解析式.
解：因为直线经过点 ，所以
.故点的坐标是 .
因经过点和点 ，所以
解得
所以直线 的函数解析式为 .
攻坚练
8.（2024·广东·中考）已知不等式的解集是 ，则一次函
数 的图象大致是( ).
B
A. B. C. D.
9.（2023·广西百色·模拟）如图4，直线分别交轴， 轴于点
，，直线分别交轴，轴于点，，点 是
内部（包括边上）的一点，则 的最大值与最小值之差为( ).
图4
A.2 B.2.5 C.3 D.3.5
图4
提示：由易知点在直线 上.画出直线
可知（图略），当为直线 与直线
的交点时，取最大值；当 为直线
与直线的交点时， 取最小值.令
,得,则.令 ,得
【答案】B
,则.故 的最大值与最小值之差为
.
图5
10.（2023·广西贵港·模拟）尊老敬老是中华民族的优
良传统.甲、乙两名同学周末相约到敬老院看望孤寡老
人.已知甲同学家在A地，乙同学家在B地，敬老院在C
地.甲、乙两名同学分别从家里出发沿同一条路前往敬
老院，他们离A地的路程随时间变化的图象如图5所示，
根据图象解答下列问题：
（1）A，B两地的路程为___ .
2
图5
（2）求乙同学离A地的路程关于时间 的函数解
析式.
解：设乙同学离A地的路程关于时间 的函数解析式为，将和 代入，得解得
所以乙同学离A地的路程关于时间的函数解析式为 .
图5
（3）甲、乙两名同学相遇时，离敬老院还有多远？
解：设甲同学离A地的路程关于时间 的函数解析式为，将 代入，得1.解得.所以甲同学离A地的路程 关于时间 的函数解析式为 .
解方程组得
所以 .
所以甲、乙两名同学相遇时，离敬老院还有 .
图6
11.（2024·浙江温州·中考模拟）如图6，在平面直角坐标
系中，点在直线上，过点 的直线
交轴于点 ．
（1）求的值和直线 对应的函数解析式.
解：将代入，得.
设直线 对 应的函数解析式为，将， 代入，得解得
所以直线 对应的函数解析式为
图6
（2）已知点在线段上，点 在直线上，求 的最大值．
解：因为点在线段 上，所以.
.
所
为 ，所以随的增大而减小.
所以当时， 取得最大值，最大值为 ．
拔尖练
12.（2024·广西河池·模拟）如图7，直线与轴交于点，与
轴交于点，将直线绕点顺时针旋转 ，与轴交于点，直线
对应的函数解析式为_ __________.
图7
图3
提示：在中，当时， ;当
时，.故，， .所以
，.如图3，过点作交 于
点，过点作轴于点 .由旋转的性质，得
.所以是等腰直角三角形， .由
，得 .又
，所以 .所以
，， .所以
，.设直线 对应的函数解析式为
，将， ，
代入，得解得 所以直线
对应的函数解析式为 .
图3
图8
13.（2025·广西梧州·模拟）综合与实践
【问题情境】水钟也叫漏刻，是古代的计时器.水
钟分为泄水型和受水型两类，图8是泄水型水钟.
水钟是根据流水的等时性原理来计时的，小红根
据这个原理制作了一个简易的泄水型水钟模型，记录了在一次实验中不同时间的水位读数，整理成下面的表格：
0 2 4 6
12 11.6 11.2 10.8
8 10 12 …
10.4 10 9.6 …
图8
【探索发现】
图9
（1）小红尝试从函数的角度进行探究，用横轴
表示泄水时间（单位： ），纵轴表示水位
读数（单位： ），建立如图9的平面直角坐
标系，请你根据上表中的数据，在图9中描出相
应的点.
解： 描点略.
（2）观察上述各点的分布规律，猜想与 之间满足哪种函数关系，并求
出关于 的函数解析式，验证上表中所给点的坐标是否满足函数解析式.
图8
解：由（1）猜想与 之间满足一次函数关系，设其解析式为，将， 代入，得
解得
所以关于 的函数解析式为.
检验:当 时，，符合题意;当 时，，符合题意;当 时，
图8
，符合题意.因此这些点的坐标都满足函数解
析式 .
【问题解决】
图8
（3）若泄水时间为 ，则水位读数是多少厘米
解：当时， .
故当泄水时间为25 min时，水位读数是 .
图8
（4）小红本次实验开始的时间为下午2时30分，则什
么时候水位读数为
解：当时，.解得 .
又因为本次实验开始的时间为下午2时30分，所以当时间为3时19分时，水位读数为 .