2026年中考数学复习课件 专题三 函数-微专题(四) 与反比例函数有关的综合题(共28张PPT)
文档属性
| 名称 | 2026年中考数学复习课件 专题三 函数-微专题(四) 与反比例函数有关的综合题(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 21:35:13 | ||
图片预览







文档简介
(共28张PPT)
复习讲义
第一篇 吃透考点
专题三 函数
微专题(四) 与反比例函数有关的综合题
类型一 反比例函数与一次函数的综合问题
方法解读 1.反比例函数与一次函数的综合问题主要有两种类型:(1)
与交点有关,常通过联立方程组,转化为一元二次方程,利用一元二次
方程的知识求解;(2)与图形性质有关,常过交点向坐标轴作垂线,
构造全等、相似图形,或利用几何条件(线段、角度等)、坐标关系,
获得等量关系求解.
图1
2.如图1,反比例函数与一次函数的图象交于点
,,求 的面积有三种思路:
(1) ;
(2) ;
(3) .
3.有关反比例函数与一次函数的不等式问题:如图2,一次函数
与反比例函数的图象交于, 两点.由
直线,和 轴将坐标平面分成四个区域.在Ⅰ,Ⅲ区域内,即
当或 时,一次函数图象在反比例函数图象的下方,即
;在Ⅱ,Ⅳ区域内,即当或 时,一次函数图
象在反比例函数图象的上方,即 .
图2
方法应用
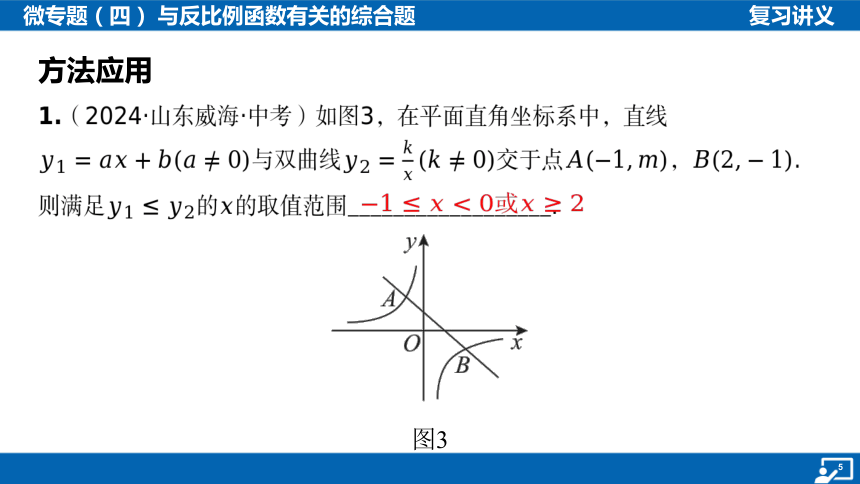
1.(2024·山东威海·中考)如图3,在平面直角坐标系中,直线
与双曲线交于点, .
则满足的 的取值范围__________________.
或
图3
2.(2025·广东珠海·模拟)如图4,一次函数 的图象与
反比例函数的图象相交于第一、三象限内的点 和
点,过点作轴的垂线,垂足为点,且 的面积为2.
图4
(1)求, 的值.
解:因为点在反比例函数 的图象上,所以 .
,所以,所以.
图4
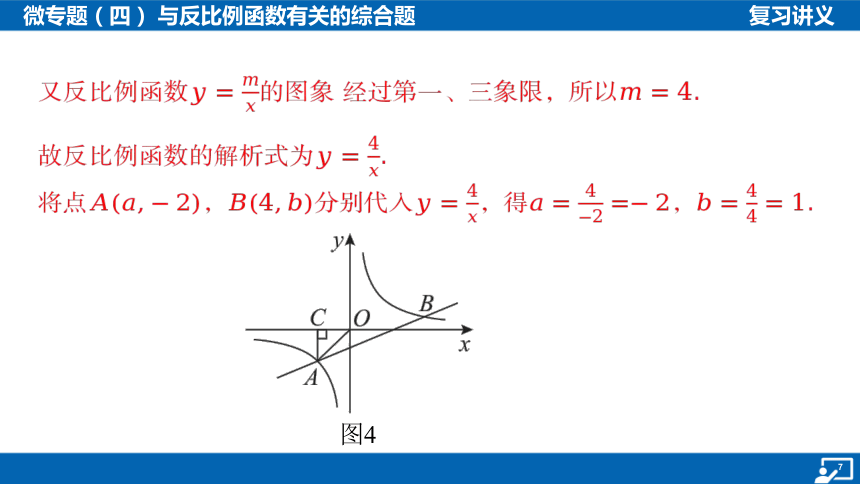
将点,分别代入,得, .
又反比例函数 的图象 经过第一、三象限,所以.
故反比例函数的解析式为 .
(2)结合图象直接写出关于的不等式 的解集.
图4
解:由(1)知,,结合图象可知 的解集为或 .
(3)在轴上取一点,当取得最大值时,求点 的坐标.
图4
解:如图10,作点关于 轴的对称点,连接交轴于点,连接 ,由对称的性质,得.
此时 取得最大值,最大值为 .
设直线 ′对应的函数解析式为 ,将点 ,代入,得
图10
图10
解得
所以直线 对应的函数解析式为.
令,得.
所以.
故当 取得最大值时,点的坐标为 .
类型二 反比例函数与几何图形的综合问题
方法解读 解反比例函数与几何图形的综合题,可以从以下四个方面进
行综合分析:
1.几何图形的性质,关键点、关键线段的特征.
2.关键点在平面直角坐标系中的位置,将其代数化、符号化,可得
到点的坐标.
3.函数图象上点的坐标特征,即函数图象上点的坐标满足对应的函
数解析式.
4.反比例函数中反比例系数 的几何意义.
方法应用
图5
3.(2023·广西南宁·模拟)如图5,在平面直角坐标
系中,点在反比例函数 的图象上,点
,在轴上,且,垂足为点,交 轴
于点,,的面积是2,则 的
值是( ).
A.1 B. C. D.2
图11
提示:如图11,连接,过点作 ,垂足
为点D.在中, ,
,所以 ,
.所以 为等边三角形.由此可
得,.由 的几何意义,得
【答案】A
.又反比例的图象在第一象限,所以 .
图6
4.(2025·武汉·模拟)如图6,在平面直角坐标系中,
矩形的一个顶点在坐标原点处,点 的坐标为
,反比例函数的图象经过点和点 ,则
的值是_____.
小锦囊过点作轴于点,过点作 轴于
点,设点的坐标为,可证,根据点 的坐标,
可推出 .由矩形对边平行且相等的性质,利用平移点的坐标规律
表示出点的坐标,再将点, 的坐标代入反比例函数的解析式,即可求
出 的值.
图12
提示:如图12,过点作轴于点,过点 作
轴于点,则 ,所以
.由矩形的性质,得.
所以 .所以 .所以
.又点的坐标为 ,所以
.设点的坐标为,则 ,
,所以.因为,,所以可通过 平移
得到,点平移到点,点平移到点.所以 因为点
,在反比例函数的图象上,所以 .解得
,.所以.所以 .
5.如图7,在平面直角坐标系中,反比例函数 在第一象限的
图象经过点,已知点,将线段绕点顺时针旋转 ,点 的
对应点恰好落在轴的点处,过点作轴于点,作
轴于点 .
图7
图7
(1)求证:四边形 为正方形.
证明:轴于点,轴于点, .
四边形 为矩形. .
, ,即 .
由旋转的性质,得.
,,,
四边形 为正方形.
图7
(2)求这个反比例函数的解析式.
解:设正方形的边长为
,, ,
,
,即 .
将代入,得 .
解得 这个反比例函数的解析式为 .
微专题练习(四)与反比例函数有关的综合题
类型一 反比例函数与一次函数的综合题
图1
1.(2022·广西桂林·模拟)如图1,在平面直角坐标系中,
点为坐标原点,直线与轴、 轴、反比例
函数的图象分别交于点,, .若
,则 的值为___.
提示:对于,令,则;令 ,
则.所以,.所以 ,
. 如图6,过点作轴于点.因为
图6
,所以,.由,得, . 所以,.所以 .因为反比例函数的图象经过点 ,所以.所以或 (舍去).
图2
2.(2024·四川成都·中考节选)如图2,在平面直角坐
标系中,直线与直线 相交于点
,与轴交于点,点 在反比例函数
的图象上.
(1)求,, 的值.
解:将代入,得 .
所以.将代入,得 .
解得.所以.
将代入 ,得.解得 .
(2)当以,,,为顶点的四边形为平行四边形时,求点 的坐标
和 的值.
图2
解:设,由(1)知,, .
以 , , , 为顶点的四边形为平行四边形有两种情况:①当 为对角线时,根据题意,得
解得
所以 ,.
图2
.
综上所述,满足条件的点的坐标为 或, .
类型二 反比例函数与几何图形的综合题
图3
3.(2023·福建·中考)如图3,正方形四个顶点分别位于
两个反比例函数和 的图象的四个分支上,则
实数 的值为( ).
A. B. C. D.3
图7
提示:连接正方形的2条对角线,由反比例函数图象的对称性和正方形的性质,可知这2条对角线相交于原点 ,如图7,过点A,B分别作 轴的垂线,垂足分别为点C,D.由正方形的性质,得 , .所以 .所以
【答案】A
.所以,即 .
解得.又因为点A在第二象限,所以 .
图4
4.(2025·贵州安顺·中考模拟)如图4,在平面直角坐标
系中,菱形的顶点在轴上,, 两点的坐
标分别为, ,直线
与反比例函数
的图象交于, 两点.
(1)求该反比例函数的解析式及 的值.
图4
解:将代入,得.解得 .
所以反比例函数的解析式为.
因为 在反比例函数的图象上,所以 .
(2)判断点 是否在该反比例函数的图象上,并说明理由.
图4
图8
解:点在反比例函数 的图象上.
理由:如图8,连接,,相交于点.
因为四边形 是菱形,所以 与 互相垂直平分.
因为 ,,所以,轴.
又点在 轴 上,所以.所以,即 .
在在中,令,得.所以点在反比例函数 的图象上.
复习讲义
第一篇 吃透考点
专题三 函数
微专题(四) 与反比例函数有关的综合题
类型一 反比例函数与一次函数的综合问题
方法解读 1.反比例函数与一次函数的综合问题主要有两种类型:(1)
与交点有关,常通过联立方程组,转化为一元二次方程,利用一元二次
方程的知识求解;(2)与图形性质有关,常过交点向坐标轴作垂线,
构造全等、相似图形,或利用几何条件(线段、角度等)、坐标关系,
获得等量关系求解.
图1
2.如图1,反比例函数与一次函数的图象交于点
,,求 的面积有三种思路:
(1) ;
(2) ;
(3) .
3.有关反比例函数与一次函数的不等式问题:如图2,一次函数
与反比例函数的图象交于, 两点.由
直线,和 轴将坐标平面分成四个区域.在Ⅰ,Ⅲ区域内,即
当或 时,一次函数图象在反比例函数图象的下方,即
;在Ⅱ,Ⅳ区域内,即当或 时,一次函数图
象在反比例函数图象的上方,即 .
图2
方法应用
1.(2024·山东威海·中考)如图3,在平面直角坐标系中,直线
与双曲线交于点, .
则满足的 的取值范围__________________.
或
图3
2.(2025·广东珠海·模拟)如图4,一次函数 的图象与
反比例函数的图象相交于第一、三象限内的点 和
点,过点作轴的垂线,垂足为点,且 的面积为2.
图4
(1)求, 的值.
解:因为点在反比例函数 的图象上,所以 .
,所以,所以.
图4
将点,分别代入,得, .
又反比例函数 的图象 经过第一、三象限,所以.
故反比例函数的解析式为 .
(2)结合图象直接写出关于的不等式 的解集.
图4
解:由(1)知,,结合图象可知 的解集为或 .
(3)在轴上取一点,当取得最大值时,求点 的坐标.
图4
解:如图10,作点关于 轴的对称点,连接交轴于点,连接 ,由对称的性质,得.
此时 取得最大值,最大值为 .
设直线 ′对应的函数解析式为 ,将点 ,代入,得
图10
图10
解得
所以直线 对应的函数解析式为.
令,得.
所以.
故当 取得最大值时,点的坐标为 .
类型二 反比例函数与几何图形的综合问题
方法解读 解反比例函数与几何图形的综合题,可以从以下四个方面进
行综合分析:
1.几何图形的性质,关键点、关键线段的特征.
2.关键点在平面直角坐标系中的位置,将其代数化、符号化,可得
到点的坐标.
3.函数图象上点的坐标特征,即函数图象上点的坐标满足对应的函
数解析式.
4.反比例函数中反比例系数 的几何意义.
方法应用
图5
3.(2023·广西南宁·模拟)如图5,在平面直角坐标
系中,点在反比例函数 的图象上,点
,在轴上,且,垂足为点,交 轴
于点,,的面积是2,则 的
值是( ).
A.1 B. C. D.2
图11
提示:如图11,连接,过点作 ,垂足
为点D.在中, ,
,所以 ,
.所以 为等边三角形.由此可
得,.由 的几何意义,得
【答案】A
.又反比例的图象在第一象限,所以 .
图6
4.(2025·武汉·模拟)如图6,在平面直角坐标系中,
矩形的一个顶点在坐标原点处,点 的坐标为
,反比例函数的图象经过点和点 ,则
的值是_____.
小锦囊过点作轴于点,过点作 轴于
点,设点的坐标为,可证,根据点 的坐标,
可推出 .由矩形对边平行且相等的性质,利用平移点的坐标规律
表示出点的坐标,再将点, 的坐标代入反比例函数的解析式,即可求
出 的值.
图12
提示:如图12,过点作轴于点,过点 作
轴于点,则 ,所以
.由矩形的性质,得.
所以 .所以 .所以
.又点的坐标为 ,所以
.设点的坐标为,则 ,
,所以.因为,,所以可通过 平移
得到,点平移到点,点平移到点.所以 因为点
,在反比例函数的图象上,所以 .解得
,.所以.所以 .
5.如图7,在平面直角坐标系中,反比例函数 在第一象限的
图象经过点,已知点,将线段绕点顺时针旋转 ,点 的
对应点恰好落在轴的点处,过点作轴于点,作
轴于点 .
图7
图7
(1)求证:四边形 为正方形.
证明:轴于点,轴于点, .
四边形 为矩形. .
, ,即 .
由旋转的性质,得.
,,,
四边形 为正方形.
图7
(2)求这个反比例函数的解析式.
解:设正方形的边长为
,, ,
,
,即 .
将代入,得 .
解得 这个反比例函数的解析式为 .
微专题练习(四)与反比例函数有关的综合题
类型一 反比例函数与一次函数的综合题
图1
1.(2022·广西桂林·模拟)如图1,在平面直角坐标系中,
点为坐标原点,直线与轴、 轴、反比例
函数的图象分别交于点,, .若
,则 的值为___.
提示:对于,令,则;令 ,
则.所以,.所以 ,
. 如图6,过点作轴于点.因为
图6
,所以,.由,得, . 所以,.所以 .因为反比例函数的图象经过点 ,所以.所以或 (舍去).
图2
2.(2024·四川成都·中考节选)如图2,在平面直角坐
标系中,直线与直线 相交于点
,与轴交于点,点 在反比例函数
的图象上.
(1)求,, 的值.
解:将代入,得 .
所以.将代入,得 .
解得.所以.
将代入 ,得.解得 .
(2)当以,,,为顶点的四边形为平行四边形时,求点 的坐标
和 的值.
图2
解:设,由(1)知,, .
以 , , , 为顶点的四边形为平行四边形有两种情况:①当 为对角线时,根据题意,得
解得
所以 ,.
图2
.
综上所述,满足条件的点的坐标为 或, .
类型二 反比例函数与几何图形的综合题
图3
3.(2023·福建·中考)如图3,正方形四个顶点分别位于
两个反比例函数和 的图象的四个分支上,则
实数 的值为( ).
A. B. C. D.3
图7
提示:连接正方形的2条对角线,由反比例函数图象的对称性和正方形的性质,可知这2条对角线相交于原点 ,如图7,过点A,B分别作 轴的垂线,垂足分别为点C,D.由正方形的性质,得 , .所以 .所以
【答案】A
.所以,即 .
解得.又因为点A在第二象限,所以 .
图4
4.(2025·贵州安顺·中考模拟)如图4,在平面直角坐标
系中,菱形的顶点在轴上,, 两点的坐
标分别为, ,直线
与反比例函数
的图象交于, 两点.
(1)求该反比例函数的解析式及 的值.
图4
解:将代入,得.解得 .
所以反比例函数的解析式为.
因为 在反比例函数的图象上,所以 .
(2)判断点 是否在该反比例函数的图象上,并说明理由.
图4
图8
解:点在反比例函数 的图象上.
理由:如图8,连接,,相交于点.
因为四边形 是菱形,所以 与 互相垂直平分.
因为 ,,所以,轴.
又点在 轴 上,所以.所以,即 .
在在中,令,得.所以点在反比例函数 的图象上.
同课章节目录
