2026年中考数学复习课件 专题四 三角形-第22讲 锐角三角函数(共48张PPT)
文档属性
| 名称 | 2026年中考数学复习课件 专题四 三角形-第22讲 锐角三角函数(共48张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 21:36:02 | ||
图片预览









文档简介
(共48张PPT)
复习讲义
第一篇 考点精讲
专题四 三角形
第22讲 锐角三角函数
聚焦核心
1.锐角三角函数
图形 锐角三角函数
__________________
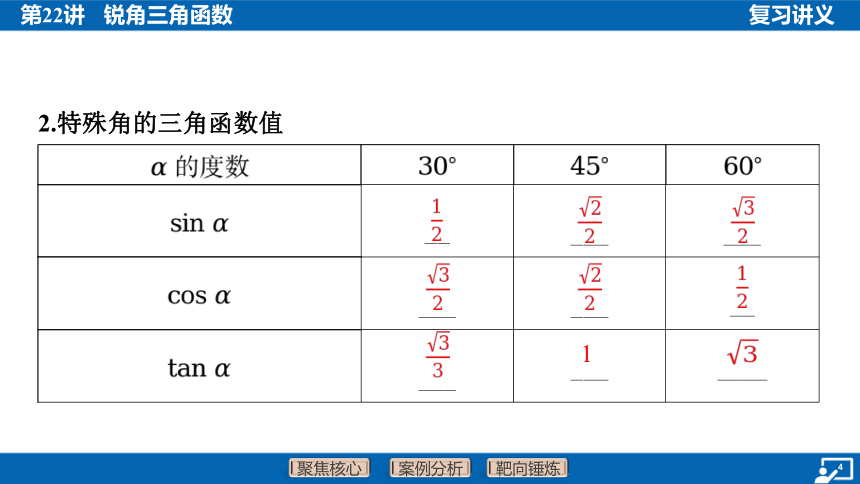
2.特殊角的三角函数值
_ _ _ __ _ __
_ __ _ __ _ _
_ __ ___ ____
1
3.直角三角形的边、角关系
图形 边、角关系 ___________________________________ 三边关系
角的关系
边角关系
90
4.解直角三角形的基本类型和方法
图形 已知条件 解法
___________________________ 一边及一锐角
图形 已知条件 解法
___________________________ 两边
续表
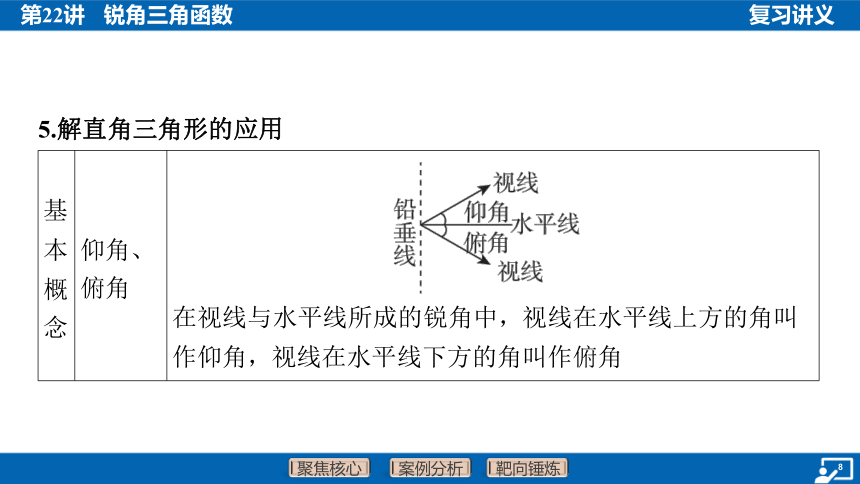
5.解直角三角形的应用
基 本 概 念 仰角、 俯角 __________________________________________________
在视线与水平线所成的锐角中,视线在水平线上方的角叫作仰角,视线在水平线下方的角叫作俯角
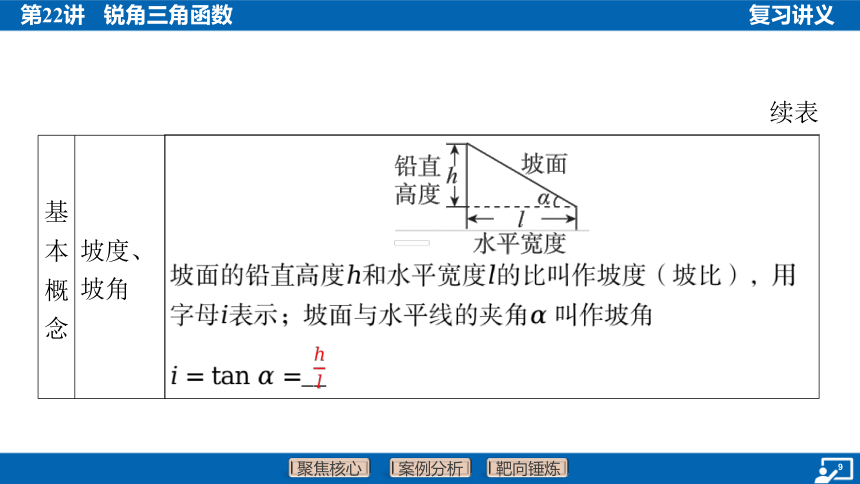
基 本 概 念 坡度、 坡角
续表
基 本 概 念 方向 角
南偏东
续表
第22讲 锐角三角函数
案例分析
考点一 锐角三角函数
名师指导
1.求锐角三角函数值时,必须找到或构造出含该锐角的直角三角形,
才能利用锐角三角函数的定义求解.
2.求锐角三角函数值时,要找准该锐角的对边与邻边.
例1 数学文化 (2024·四川资阳·中考)第14届国际数学教育大会 会标如图1所示,会标中心的图案来源于我国古代数学家赵爽的“弦图”.图2所示的“弦图”是由四个全等的直角三角形和一个小正方形 拼成的大正方形.若,则 的值为( ).
图1
图2
A. B. C. D.
提示:设,则.因为,四边形 为正
方形,所以,.从而得 .由勾股定理,
得.所以 .
图1
图2
【答案】C
思路点拨 观察图形可发现是 的一个锐角,它的对边是
,故求出与的比值,即可得到 的值.
考点专练
1.(2025·四川攀枝花·中考改编)中,,,的对边分别为 ,
,.已知,,,则 的值为( ).
C
A. B. C. D.
图3
2.(2025·湖南邵阳·模拟) 在正方形网格纸中的位置
如图3,则 的值为( ).
D
A. B. C. D.
考点二 解直角三角形
名师指导
1.在一个三角形中,已知角度或锐角的三角函数值求线段的长,通
常考虑利用解直角三角形的知识求解.
2.解题时,如果题目中没有已知的直角三角形,那么常作三角形的
高构造直角三角形.
图4
例2 (2024·浙江·中考)如图4,在 中,,是边上的中线, ,, .
(1)求 的长.
思路点拨
解: ,,, 由勾股定理得
,
.
图4
(2)求 的值.
图4
解: 是边上的中线,
, .
.
思路点拨
考点专练
图5
3.(2024·甘肃临夏·中考)如图5,在 中,
,,则 的长是( ).
B
A.3 B.6 C.8 D.9
4.(2025·广西桂林·模拟改编)在中, , ,
,则 ____.
16
图6
5.(2025·广西河池·模拟)如图6,在 中,
,为上一点,, ,
.
(1)求 的长.
解:在中, ,,,可设 ,.
由,得.
解得 ,(不合题意,舍去)
, ,
.
图6
(2)求 的值.
解:过点作于点.
在 中,,可设, .
由,得 .
解得,(不合题意,舍去)
.
∴ .
考点三 解直角三角形的实际应用
名师指导
用锐角三角函数知识解决生活中的实际问题,实质上就是解直角三
角形,常见的有方位角问题、坡度(坡比)问题、距离测量问题、高度
测量问题等.解决这类问题要把握好各类图形的特征,构造出直角三角
形,利用锐角三角函数和勾股定理等知识解直角三角形.
图7
例3 跨学科题(2024·安徽·中考)科技社团在学校游
泳池进行一次光的折射实验,如图7,光线自点 处发
出,经水面点折射到池底点处.已知 与水平线的
夹角,点到水面的距离,点
处水深为,点到池壁的水平距离 .
点,, 在同一条竖直线上,所有点都在同一竖直
平面内.记入射角为 ,折射角为 ,求 的值.
(结果精确到0.1;参考数据:, ,
)
图7
思路点拨 观察图形,可发现 和 都不在直
角三角形中,需要将它们等量代换到直角三角
形中或构造直角三角形.由题意可知,法线与
池壁平行,则 ,可在 中探
究 的值.过点 作池底的垂线,则构造出
含 角的直角三角形,在这个直角三角形中
探究 的值.
图7
解:过点作于点 .
由题意可知,,, ,
,
.
考点专练
图8
6.(2024·吉林长春·中考)2024年5月29日16时12分,长春净
月一号卫星搭乘谷神星一号火箭在黄海海域成功发射.如图8,
当火箭上升到点时,位于海平面处的雷达测得点到点
的距离为,仰角为 ,则此时火箭距海平面的高度
为( ).
A
A. B. C. D.
图9
7.(2025·广东广州·中考模拟)如图9,海中有一座小岛,在
点测得小岛在北偏东 方向上,渔船从 点出发,由西
向东航行到达点,在点测得小岛 恰好在正北
方向上,此时渔船与小岛 的距离为( ).
D
A. B.
C. D.
8.(2024·四川眉山·中考)如图10,斜坡的坡度 ,在斜坡上有一棵垂直于水平面的大树,当太阳光与水平面的夹角为 时,大树在斜坡上的影子长为,则大树的高为____________ .
图10
提示:如图28,过点作水平地面的平行线,交 的延长线于点,则.在 中, .
设, ,
图28
图28
【答案】
.由此可得,, .
,
.故大树的高度为 .
9.传统文化(2024·四川成都·中考)如图11,我国古代运用“土圭之法”判别四季.夏至时日影最短,冬至时日影最长,春分和秋分时日影长度等于夏至和冬至日影长度的平均数.某地学生运用此法进行实践探索,如图12,产生日影的杆子垂直于地面, 的长为8.在夏至时,杆子在太阳光线照射下产生的日影为;在冬至时,杆子 在太阳光线照射下产生的日影为.已知 ,
图11
图12
,求春分和秋分时杆子 的日影长度.(结果精确到0.1;参考数据:
,, ,,, )
图11
图12
解:在中,, ,
.在中, , ,
.
故春分和秋分时杆子的日影长度为 .
图11
图12
第22讲 锐角三角函数
靶向锤炼
靶向练
1.(2025·江苏无锡·中考模拟) 的值为( ).
B
A. B. C. D.
图1
2.(2024·云南·中考)如图1,在 中,若
,,,则 的值为( ).
C
A. B. C. D.
图2
3.(2025·广西南宁·模拟)如图2,某水库堤坝横断
面迎水坡的坡角为 , ,堤坝高
,则迎水坡面 的长度为( ).
B
A. B. C. D.
图3
4.(2025·湖南益阳·中考改编)如图3,在平面直角坐标
系中,有三点,,,则
的值为( ).
C
A. B. C. D.
图4
5.(2024·四川雅安·中考)在数学课外实践活动
中,某小组测量一栋楼房 的高度(如图4),
他们在处仰望楼顶,测得仰角为 ,再往楼
的方向前进至处,测得仰角为 ,那么
这栋楼的高度为( ).(人的身高忽略不计)
A. B. C. D.
提示:由 , ,得 .从而得 .在R中, ,所以 .
A
6.(2025·湖南长沙·模拟)如图5,在中, ,
,是边的中点,则的长为_________.(用含 的三角函数值表示)
图5
图6
7.(2025·安徽合肥·模拟)如图6,在 中,已知 , ,,点 在边上,且 ,求 的长.(结果精确到,参考数据: ,, ,,, )
图6
解:在中, , ,
,∴ .
在 中,, ,
.
攻坚练
8.(2025·四川眉山·中考模拟)如图7,一艘渔船在海上点处测得灯塔 在它
的北偏东 方向,渔船向正东方向航行到达点 处,测得灯
塔在它的北偏东 方向.若渔船继续向正东方向航行,则渔船与灯塔
的最短距离是_________ .(结果保留根号)
图7
图7
提示:过点作于点 .根据题意可知,
, .在 中,
.在 中,
, ,即
.解得.故渔船与灯塔 的
最短距离是 .
9.(2024·江西·中考)将图8所示的七巧板拼成图9所示的四边形 ,
连接,则 的值为__.
图8
图9
提示:设与的交点为.由题意可知 ,从而
得.又,所以四边形是平行四边形.由此可得 与
互相平分,即.又,所以.在
中, .
图10
10.(2024·吉林·中考)吉林省广播电视塔又称“吉
塔”.某直升机于空中 处探测到吉塔,此时飞行高度
,如图10.从直升机上看塔尖 的俯角
,看塔底的俯角 ,求吉
塔的高度.(结果精确到 ,参考数据:
,, )
图41
解:如图41,过点作,垂足为点
,,, .
四边形是矩形.
,
, ,
.
.
在中,,∴
.
答:吉塔的高度约为 .
拔尖练
11.(2024·湖南张家界·中考模拟)阅读下列材料:
在中,,,所对的边分别为,,.求证: .
图11
证明:如图11,过点作于点 ,则
在中, ,
在中, ,
.
根据上面的材料,解决下列问题:
图12
(1)如图12,在中,,, 所对的边分别
为,,.求证: .
图42
证明:如图42,过点作于点.
在 中,.
在 中,
.
(2)为了办好湖南省首届旅游发展大会,张家界市积极优化旅游环境.如图13,规划中的一片三角形区域需美化,已知 , , ,求这片区域的面积.(结果保留根号,参考数据:, )
图13
图43
解:如图43,过点作于点
, ,∴ .
在中, .
由(1)中结论知,,即, .
∴ .
复习讲义
第一篇 考点精讲
专题四 三角形
第22讲 锐角三角函数
聚焦核心
1.锐角三角函数
图形 锐角三角函数
__________________
2.特殊角的三角函数值
_ _ _ __ _ __
_ __ _ __ _ _
_ __ ___ ____
1
3.直角三角形的边、角关系
图形 边、角关系 ___________________________________ 三边关系
角的关系
边角关系
90
4.解直角三角形的基本类型和方法
图形 已知条件 解法
___________________________ 一边及一锐角
图形 已知条件 解法
___________________________ 两边
续表
5.解直角三角形的应用
基 本 概 念 仰角、 俯角 __________________________________________________
在视线与水平线所成的锐角中,视线在水平线上方的角叫作仰角,视线在水平线下方的角叫作俯角
基 本 概 念 坡度、 坡角
续表
基 本 概 念 方向 角
南偏东
续表
第22讲 锐角三角函数
案例分析
考点一 锐角三角函数
名师指导
1.求锐角三角函数值时,必须找到或构造出含该锐角的直角三角形,
才能利用锐角三角函数的定义求解.
2.求锐角三角函数值时,要找准该锐角的对边与邻边.
例1 数学文化 (2024·四川资阳·中考)第14届国际数学教育大会 会标如图1所示,会标中心的图案来源于我国古代数学家赵爽的“弦图”.图2所示的“弦图”是由四个全等的直角三角形和一个小正方形 拼成的大正方形.若,则 的值为( ).
图1
图2
A. B. C. D.
提示:设,则.因为,四边形 为正
方形,所以,.从而得 .由勾股定理,
得.所以 .
图1
图2
【答案】C
思路点拨 观察图形可发现是 的一个锐角,它的对边是
,故求出与的比值,即可得到 的值.
考点专练
1.(2025·四川攀枝花·中考改编)中,,,的对边分别为 ,
,.已知,,,则 的值为( ).
C
A. B. C. D.
图3
2.(2025·湖南邵阳·模拟) 在正方形网格纸中的位置
如图3,则 的值为( ).
D
A. B. C. D.
考点二 解直角三角形
名师指导
1.在一个三角形中,已知角度或锐角的三角函数值求线段的长,通
常考虑利用解直角三角形的知识求解.
2.解题时,如果题目中没有已知的直角三角形,那么常作三角形的
高构造直角三角形.
图4
例2 (2024·浙江·中考)如图4,在 中,,是边上的中线, ,, .
(1)求 的长.
思路点拨
解: ,,, 由勾股定理得
,
.
图4
(2)求 的值.
图4
解: 是边上的中线,
, .
.
思路点拨
考点专练
图5
3.(2024·甘肃临夏·中考)如图5,在 中,
,,则 的长是( ).
B
A.3 B.6 C.8 D.9
4.(2025·广西桂林·模拟改编)在中, , ,
,则 ____.
16
图6
5.(2025·广西河池·模拟)如图6,在 中,
,为上一点,, ,
.
(1)求 的长.
解:在中, ,,,可设 ,.
由,得.
解得 ,(不合题意,舍去)
, ,
.
图6
(2)求 的值.
解:过点作于点.
在 中,,可设, .
由,得 .
解得,(不合题意,舍去)
.
∴ .
考点三 解直角三角形的实际应用
名师指导
用锐角三角函数知识解决生活中的实际问题,实质上就是解直角三
角形,常见的有方位角问题、坡度(坡比)问题、距离测量问题、高度
测量问题等.解决这类问题要把握好各类图形的特征,构造出直角三角
形,利用锐角三角函数和勾股定理等知识解直角三角形.
图7
例3 跨学科题(2024·安徽·中考)科技社团在学校游
泳池进行一次光的折射实验,如图7,光线自点 处发
出,经水面点折射到池底点处.已知 与水平线的
夹角,点到水面的距离,点
处水深为,点到池壁的水平距离 .
点,, 在同一条竖直线上,所有点都在同一竖直
平面内.记入射角为 ,折射角为 ,求 的值.
(结果精确到0.1;参考数据:, ,
)
图7
思路点拨 观察图形,可发现 和 都不在直
角三角形中,需要将它们等量代换到直角三角
形中或构造直角三角形.由题意可知,法线与
池壁平行,则 ,可在 中探
究 的值.过点 作池底的垂线,则构造出
含 角的直角三角形,在这个直角三角形中
探究 的值.
图7
解:过点作于点 .
由题意可知,,, ,
,
.
考点专练
图8
6.(2024·吉林长春·中考)2024年5月29日16时12分,长春净
月一号卫星搭乘谷神星一号火箭在黄海海域成功发射.如图8,
当火箭上升到点时,位于海平面处的雷达测得点到点
的距离为,仰角为 ,则此时火箭距海平面的高度
为( ).
A
A. B. C. D.
图9
7.(2025·广东广州·中考模拟)如图9,海中有一座小岛,在
点测得小岛在北偏东 方向上,渔船从 点出发,由西
向东航行到达点,在点测得小岛 恰好在正北
方向上,此时渔船与小岛 的距离为( ).
D
A. B.
C. D.
8.(2024·四川眉山·中考)如图10,斜坡的坡度 ,在斜坡上有一棵垂直于水平面的大树,当太阳光与水平面的夹角为 时,大树在斜坡上的影子长为,则大树的高为____________ .
图10
提示:如图28,过点作水平地面的平行线,交 的延长线于点,则.在 中, .
设, ,
图28
图28
【答案】
.由此可得,, .
,
.故大树的高度为 .
9.传统文化(2024·四川成都·中考)如图11,我国古代运用“土圭之法”判别四季.夏至时日影最短,冬至时日影最长,春分和秋分时日影长度等于夏至和冬至日影长度的平均数.某地学生运用此法进行实践探索,如图12,产生日影的杆子垂直于地面, 的长为8.在夏至时,杆子在太阳光线照射下产生的日影为;在冬至时,杆子 在太阳光线照射下产生的日影为.已知 ,
图11
图12
,求春分和秋分时杆子 的日影长度.(结果精确到0.1;参考数据:
,, ,,, )
图11
图12
解:在中,, ,
.在中, , ,
.
故春分和秋分时杆子的日影长度为 .
图11
图12
第22讲 锐角三角函数
靶向锤炼
靶向练
1.(2025·江苏无锡·中考模拟) 的值为( ).
B
A. B. C. D.
图1
2.(2024·云南·中考)如图1,在 中,若
,,,则 的值为( ).
C
A. B. C. D.
图2
3.(2025·广西南宁·模拟)如图2,某水库堤坝横断
面迎水坡的坡角为 , ,堤坝高
,则迎水坡面 的长度为( ).
B
A. B. C. D.
图3
4.(2025·湖南益阳·中考改编)如图3,在平面直角坐标
系中,有三点,,,则
的值为( ).
C
A. B. C. D.
图4
5.(2024·四川雅安·中考)在数学课外实践活动
中,某小组测量一栋楼房 的高度(如图4),
他们在处仰望楼顶,测得仰角为 ,再往楼
的方向前进至处,测得仰角为 ,那么
这栋楼的高度为( ).(人的身高忽略不计)
A. B. C. D.
提示:由 , ,得 .从而得 .在R中, ,所以 .
A
6.(2025·湖南长沙·模拟)如图5,在中, ,
,是边的中点,则的长为_________.(用含 的三角函数值表示)
图5
图6
7.(2025·安徽合肥·模拟)如图6,在 中,已知 , ,,点 在边上,且 ,求 的长.(结果精确到,参考数据: ,, ,,, )
图6
解:在中, , ,
,∴ .
在 中,, ,
.
攻坚练
8.(2025·四川眉山·中考模拟)如图7,一艘渔船在海上点处测得灯塔 在它
的北偏东 方向,渔船向正东方向航行到达点 处,测得灯
塔在它的北偏东 方向.若渔船继续向正东方向航行,则渔船与灯塔
的最短距离是_________ .(结果保留根号)
图7
图7
提示:过点作于点 .根据题意可知,
, .在 中,
.在 中,
, ,即
.解得.故渔船与灯塔 的
最短距离是 .
9.(2024·江西·中考)将图8所示的七巧板拼成图9所示的四边形 ,
连接,则 的值为__.
图8
图9
提示:设与的交点为.由题意可知 ,从而
得.又,所以四边形是平行四边形.由此可得 与
互相平分,即.又,所以.在
中, .
图10
10.(2024·吉林·中考)吉林省广播电视塔又称“吉
塔”.某直升机于空中 处探测到吉塔,此时飞行高度
,如图10.从直升机上看塔尖 的俯角
,看塔底的俯角 ,求吉
塔的高度.(结果精确到 ,参考数据:
,, )
图41
解:如图41,过点作,垂足为点
,,, .
四边形是矩形.
,
, ,
.
.
在中,,∴
.
答:吉塔的高度约为 .
拔尖练
11.(2024·湖南张家界·中考模拟)阅读下列材料:
在中,,,所对的边分别为,,.求证: .
图11
证明:如图11,过点作于点 ,则
在中, ,
在中, ,
.
根据上面的材料,解决下列问题:
图12
(1)如图12,在中,,, 所对的边分别
为,,.求证: .
图42
证明:如图42,过点作于点.
在 中,.
在 中,
.
(2)为了办好湖南省首届旅游发展大会,张家界市积极优化旅游环境.如图13,规划中的一片三角形区域需美化,已知 , , ,求这片区域的面积.(结果保留根号,参考数据:, )
图13
图43
解:如图43,过点作于点
, ,∴ .
在中, .
由(1)中结论知,,即, .
∴ .
同课章节目录
