第十章 静电场中的能量(预习衔接.夯实基础.含解析)2025-2026学年高二上学期物理必修第三册人教版(2019)
文档属性
| 名称 | 第十章 静电场中的能量(预习衔接.夯实基础.含解析)2025-2026学年高二上学期物理必修第三册人教版(2019) |  | |
| 格式 | docx | ||
| 文件大小 | 401.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-07-18 17:54:27 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
预习衔接.夯实基础 静电场中的能量
一.选择题(共4小题)
1.(2024秋 锡山区校级期末)两个点电荷,电性未知、电荷量大小分别为4q和q,其电场线如图所示(未标明方向,且未画出对称轴附近的电场线),A、B、C、D为对称轴上的四个点,且满足AB=BC=CD,则( )
A.A、D两点的场强方向一定相反
B.从D点向左至无穷远,场强不断减小
C.若电荷量为4q的点电荷为负电荷,则电子从A向B移动的过程中,电势能减小
D.若电荷量为4q的点电荷为负电荷,则A点电势低于D点电势
2.(2024秋 朝阳区期末)有人认为在两个带电导体之间可以存在如图所示的静电场,它的电场线相互平行,间距不等。关于此“静电场”,下列说法正确的是( )
A.该电场一定存在,是个特殊的匀强电场
B.该电场一定存在,可以通过两个匀强电场叠加产生
C.根据图中a、b两点电场强度方向相同,大小不同,可判断该电场不存在
D.通过试探电荷沿不同路径从图中a点移动到b点,电场力做功不同,可判断该电场不存在
3.(2024秋 大连期末)有研究表明,当兴奋情绪传播时,在人的体表可以测出与之对应的电势变化。某一瞬间人体表面的电势分布图如图所示,图中实线为等差等势面,标在等势面上的数值分别表示该等势面的电势,a、b、c、d为等势面上的点,该电场可等效为两等量异种电荷产生的电场,a、b为两电荷连线上对称的两点,c、d为两电荷连线中垂线上对称的两点。下列说法中正确的是( )
A.a、b两点的电场强度大小相等,方向相反
B.c点的电势大于d点的电势
C.将带正电的试探电荷从b点移到d点,电场力做负功
D.负电荷在c点的电势能小于在a点的电势能
4.(2024春 新吴区校级期末)一匀强电场的方向平行于xOy平面,平面内a、b、c三点的位置如图所示,三点的电势分别为10V、10V、22V。下列说法不正确的是( )
A.电场强度的大小为2.5V/cm
B.坐标原点处的电势为﹣2V
C.电子在a点的电势能比在c点的低12eV
D.电子从b点运动到c点,静电力做功为12eV
二.多选题(共3小题)
(多选)5.(2024春 大连期末)如图所示,在地面上方的水平匀强电场中,一个质量为m、带正电的电荷量为q的小球,系在一根长为R的绝缘细线的一端,可以在竖直平面内绕O点做圆周运动。AB为圆周的水平直径,CD为竖直直径。已知重力加速度的大小为g,电场强度。
若小球恰能在竖直平面内绕O点做圆周运动,不计空气阻力,则下列说法正确的是( )
A.小球运动到C点时细线的拉力最大
B.小球运动到B点时的电势能最大
C.小球运动到B点时的机械能最大
D.小球运动过程中的最小速度为
(多选)6.(2024秋 海淀区期末)某静电场的电势φ在x轴上的分布如图所示,B、C是x轴上关于坐标原点O对称的两点。一个带负电的粒子仅在电场力作用下,以O点为中心、沿x轴方向在B、C两点间做周期性往复运动。下列说法正确的是( )
A.从B运动到C的过程中,电场力先做正功,后做负功
B.从B运动到O的过程中,粒子的加速度先减小后增大
C.粒子在O点的电势能最小
D.粒子的运动是简谐运动
(多选)7.(2024春 湖南期末)如图甲所示,粗糙、绝缘的水平地面上,一质量m=1kg的带负电小滑块(可视为质点)在x=1m处以v0=2m/s的初速度沿x轴正方向运动,滑块与地面间的动摩擦因数μ=0.05。在x=0及x=5m处有两个电性未知,电荷量分别为Q1、Q2的点电荷场源,滑块在不同位置所具有的电势能Ep如图乙所示,P点是图线最低点,虚线AB是图像在x=1m处的切线,g=10m/s2下列说法正确的选项是( )
A.滑块在x=3m处所受合外力小于 0.5N
B.两场源电荷均带负电,且|Q1|>|Q2|
C.滑块向右运动过程中,速度始终减小
D.滑块向右一定可以经过x=4m处的位置
三.填空题(共4小题)
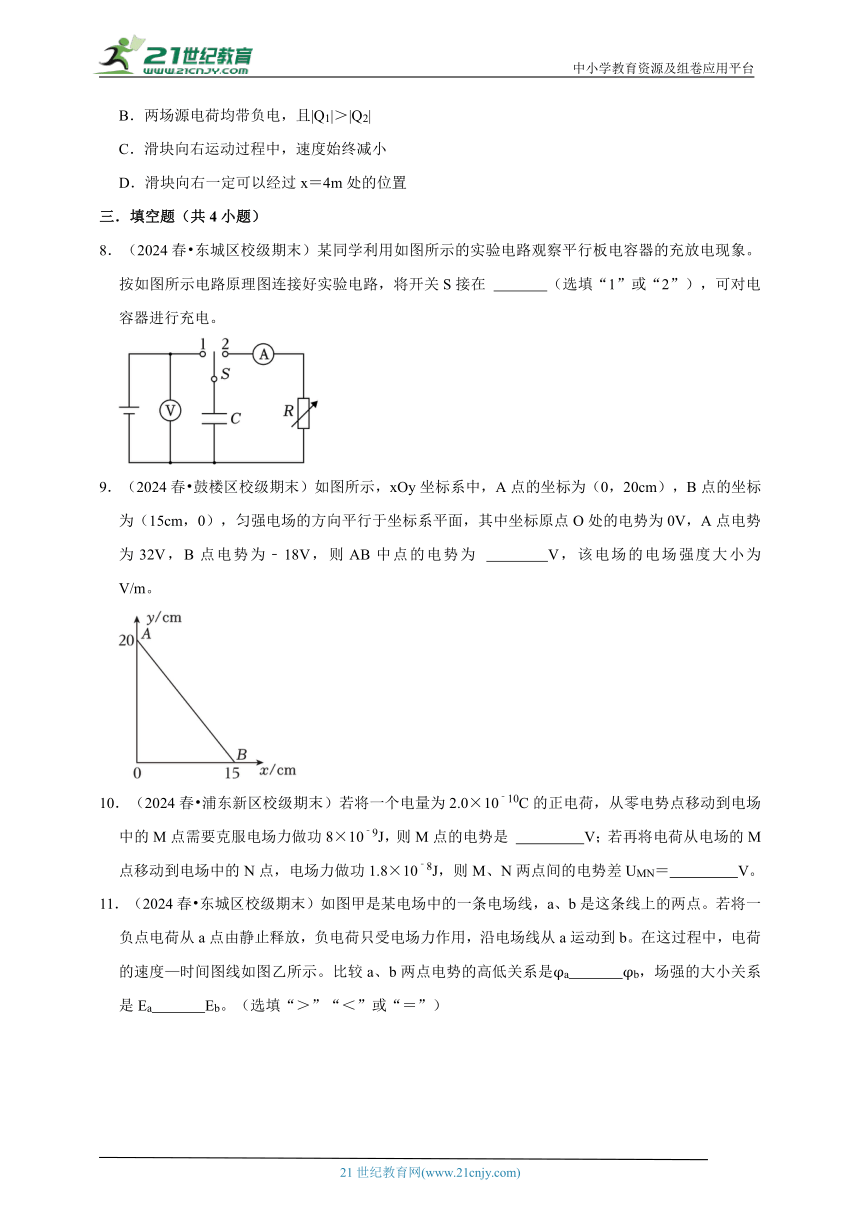
8.(2024春 东城区校级期末)某同学利用如图所示的实验电路观察平行板电容器的充放电现象。按如图所示电路原理图连接好实验电路,将开关S接在 (选填“1”或“2”),可对电容器进行充电。
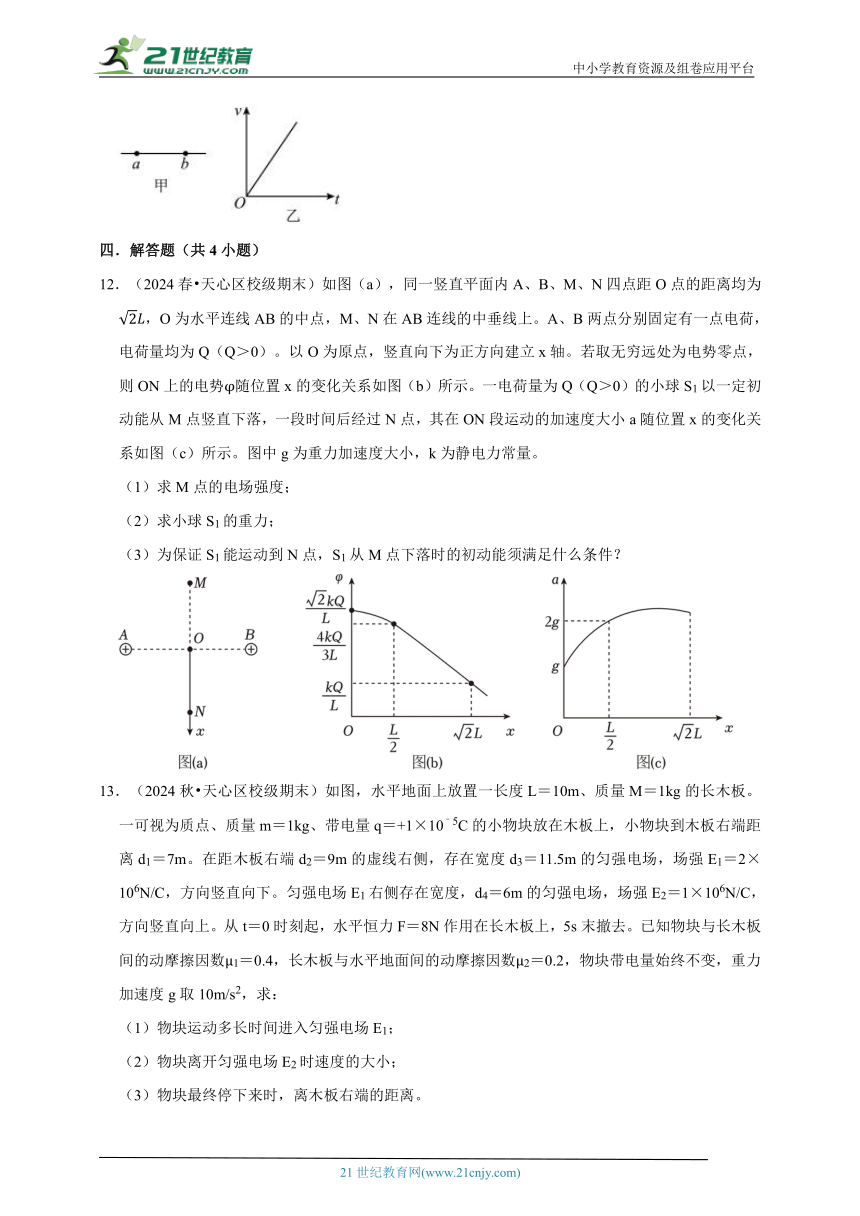
9.(2024春 鼓楼区校级期末)如图所示,xOy坐标系中,A点的坐标为(0,20cm),B点的坐标为(15cm,0),匀强电场的方向平行于坐标系平面,其中坐标原点O处的电势为0V,A点电势为32V,B点电势为﹣18V,则AB中点的电势为 V,该电场的电场强度大小为 V/m。
10.(2024春 浦东新区校级期末)若将一个电量为2.0×10﹣10C的正电荷,从零电势点移动到电场中的M点需要克服电场力做功8×10﹣9J,则M点的电势是 V;若再将电荷从电场的M点移动到电场中的N点,电场力做功1.8×10﹣8J,则M、N两点间的电势差UMN= V。
11.(2024春 东城区校级期末)如图甲是某电场中的一条电场线,a、b是这条线上的两点。若将一负点电荷从a点由静止释放,负电荷只受电场力作用,沿电场线从a运动到b。在这过程中,电荷的速度—时间图线如图乙所示。比较a、b两点电势的高低关系是φa φb,场强的大小关系是Ea Eb。(选填“>”“<”或“=”)
四.解答题(共4小题)
12.(2024春 天心区校级期末)如图(a),同一竖直平面内A、B、M、N四点距O点的距离均为,O为水平连线AB的中点,M、N在AB连线的中垂线上。A、B两点分别固定有一点电荷,电荷量均为Q(Q>0)。以O为原点,竖直向下为正方向建立x轴。若取无穷远处为电势零点,则ON上的电势φ随位置x的变化关系如图(b)所示。一电荷量为Q(Q>0)的小球S1以一定初动能从M点竖直下落,一段时间后经过N点,其在ON段运动的加速度大小a随位置x的变化关系如图(c)所示。图中g为重力加速度大小,k为静电力常量。
(1)求M点的电场强度;
(2)求小球S1的重力;
(3)为保证S1能运动到N点,S1从M点下落时的初动能须满足什么条件?
13.(2024秋 天心区校级期末)如图,水平地面上放置一长度L=10m、质量M=1kg的长木板。一可视为质点、质量m=1kg、带电量q=+1×10﹣5C的小物块放在木板上,小物块到木板右端距离d1=7m。在距木板右端d2=9m的虚线右侧,存在宽度d3=11.5m的匀强电场,场强E1=2×106N/C,方向竖直向下。匀强电场E1右侧存在宽度,d4=6m的匀强电场,场强E2=1×106N/C,方向竖直向上。从t=0时刻起,水平恒力F=8N作用在长木板上,5s末撤去。已知物块与长木板间的动摩擦因数μ1=0.4,长木板与水平地面间的动摩擦因数μ2=0.2,物块带电量始终不变,重力加速度g取10m/s2,求:
(1)物块运动多长时间进入匀强电场E1;
(2)物块离开匀强电场E2时速度的大小;
(3)物块最终停下来时,离木板右端的距离。
14.(2024秋 厦门期末)如图甲所示,一倾角为30°足够长的绝缘斜面固定在水平地面上,质量为m、电荷量为﹣q(q>0)的物块A压缩轻质绝缘微型弹簧a后锁定(A与弹簧不拴接)。空间中存在沿斜面向上、大小E(g为重力加速度)的匀强电场。质量为2m、电荷量为+q的物块B静止在斜面上端,B左侧固定有处于原长的轻质绝缘弹簧b,A、B与斜面的滑动摩擦力大小分别为mg、mg,最大静摩擦力等于滑动摩擦力。
t=0时解除锁定,弹簧的弹性势能Ep瞬间全部转化为A的动能,A运动距离L后于t1时刻到达P点,此时速度为v1、加速度为0,且未与弹簧b接触;t2时刻,A到达Q点,速度达到最大值2v1,弹簧b的弹力大小为mg,此过程中A的v﹣t图像如图乙所示。已知A、B的电荷量始终保持不变,两者间的库仑力等效为真空中点电荷间的静电力,静电力常量为k,弹簧始终在弹性限度内。求:
(1)弹射过程弹簧a对A冲量的大小;
(2)A从开始运动到P点的过程中,B对A库仑力所做的功;
(3)A到达P点时,A与B之间的距离;
(4)A从P点运动到Q点的过程中,A、B系统(含弹簧b)的电势能变化量与弹性势能变化量的总和。
15.(2024春 宿州期末)如图所示,由电子枪发出的电子从静止开始经加速电场加速后,沿平行于板面的方向射入偏转电场,并从另一侧射出。已知电子质量为m,电荷量为e,加速电场电压为U0,偏转电场可视为匀强电场,偏转电极YY'之间电压为U,极板长度为L,两极板间距离为d。不计电子重力和电子间相互作用,求:
(1)电子离开加速电场时的速度大小v0;
(2)电子在偏转电场中的加速度大小a;
(3)电子从偏转电场射出时沿垂直板面方向的偏转距离y。
预习衔接.夯实基础 静电场中的能量
参考答案与试题解析
一.选择题(共4小题)
1.(2024秋 锡山区校级期末)两个点电荷,电性未知、电荷量大小分别为4q和q,其电场线如图所示(未标明方向,且未画出对称轴附近的电场线),A、B、C、D为对称轴上的四个点,且满足AB=BC=CD,则( )
A.A、D两点的场强方向一定相反
B.从D点向左至无穷远,场强不断减小
C.若电荷量为4q的点电荷为负电荷,则电子从A向B移动的过程中,电势能减小
D.若电荷量为4q的点电荷为负电荷,则A点电势低于D点电势
【考点】电场力做功与电势能变化的关系;电势的定义、单位和物理意义及用定义式计算电势;电场线的定义及基本特征.
【专题】比较思想;图析法;电场力与电势的性质专题;理解能力.
【答案】D
【分析】根据点电荷场强公式E=k和电场的叠加原理确定A、D两点的场强方向关系,并分析场强的变化情况;根据电场力做功情况判断电势能的变化情况;根据离正点电荷越近电势越高,离负点电荷越近电势越低,分析A点与D点电势高低。
【解答】解:AB、由图中电场线分布情况可知,两点电荷为异种电荷,且B处电场线密,则B处电荷量为4q,C处电荷量为q。设电荷量为4q的点电荷为负电荷,电荷量为q的点电荷为正电荷,并设AB=BC=CD=r,则A点的场强大小为,(方向指向负点电荷4q),D点的场强大小为。
由于D点的场强大小为零,无穷远处场强也为零,所以从D点向左至无穷远,场强先增大后减小,故AB错误;
C、若电荷量为4q的点电荷为负电荷,电子从A向B移动的过程中,场强方向由A指向B,电子所受的电场力与运动方向相反,电场力对电子做负功,所以电子的电势能增加,故C错误;
D、若电荷量为4q的点电荷为负电荷,则B处为4q负电荷,C处q为正电荷,根据离正点电荷越近电势越高,离负点电荷越近电势越低,则知﹣4q点电荷在A点的电势低于D点电势,+q点电荷在A点的电势低于D点电势,由电场的叠加原理可知,A点电势低于D点电势,故D正确。
故选:D。
【点评】解答本题的关键要掌握电场的叠加原理,根据场强的合成分析合场强的方向,判断电场力做功情况,从而分析电势能的变化情况。
2.(2024秋 朝阳区期末)有人认为在两个带电导体之间可以存在如图所示的静电场,它的电场线相互平行,间距不等。关于此“静电场”,下列说法正确的是( )
A.该电场一定存在,是个特殊的匀强电场
B.该电场一定存在,可以通过两个匀强电场叠加产生
C.根据图中a、b两点电场强度方向相同,大小不同,可判断该电场不存在
D.通过试探电荷沿不同路径从图中a点移动到b点,电场力做功不同,可判断该电场不存在
【考点】电场力做功与电势能变化的关系;电场线的定义及基本特征.
【专题】定性思想;极端假设法;电场力与电势的性质专题;推理论证能力.
【答案】D
【分析】根据匀强电场的特点判断AB;根据等势面的特点和电势差与场强的关系判断C;根据电场力做功特点判断D。
【解答】解:A.电场线相互平行,说明电场中各点的场强方向相同,而电场线间距不等说明电场中各点场强大小不是处处相等,不是匀强电场,故A错误;
B.将两个匀强电场叠加,获得的电场仍为匀强电场,故B错误;
C:如果存在这样的电场,根据等势面的特点,它的等势面ac、bd应该如下图所示
a、d两点的电势差Uad应该等于c、b两点的电势差Ucb,即
Uad=Ucb
从图中可以看出,a、d两点的距离等于c、b两点的距离,ad处的场强大于cb处的场强。根据
U=Ed
可得
Uad>Ucb
所以这样的电场不可能存在,但等势面上各点的场强不一定大小相等,故C错误;
D.如下图所示
粒子沿两个不同的路径,从a→d→b和从a→c→b,电场力做功不相同(Uad>Ucb),即电场力做功与路径有关,违背了静电场的基本性质,所以这样的电场不可能存在,故D正确。
故选:D。
【点评】知道电场力做功与其路径无关,只与初末位置的电势差有关是解题的关键,另外掌握匀强电场的特点是解题的基础。
3.(2024秋 大连期末)有研究表明,当兴奋情绪传播时,在人的体表可以测出与之对应的电势变化。某一瞬间人体表面的电势分布图如图所示,图中实线为等差等势面,标在等势面上的数值分别表示该等势面的电势,a、b、c、d为等势面上的点,该电场可等效为两等量异种电荷产生的电场,a、b为两电荷连线上对称的两点,c、d为两电荷连线中垂线上对称的两点。下列说法中正确的是( )
A.a、b两点的电场强度大小相等,方向相反
B.c点的电势大于d点的电势
C.将带正电的试探电荷从b点移到d点,电场力做负功
D.负电荷在c点的电势能小于在a点的电势能
【考点】等势面及其与电场线的关系;电场力做功与电势能变化的关系;电势的定义、单位和物理意义及用定义式计算电势.
【专题】定性思想;推理法;电场力与电势的性质专题;理解能力.
【答案】C
【分析】根据等量异种电荷的电场线分布进行分析;根据电势的大小求解ab两点、bc两点的电势差。
【解答】解:A.该电势分布图可等效为等量异种电荷产生的,a、b为两电荷连线上对称的两点,根据等量异种电荷的电场的特点,可以判断、这两个对称点的电场强度大小相等、方向相同,故A错误;
B.c、d两点位于等量异种点电荷连线的中垂线上,该中垂线是一条等势线,则c点的电势等于d点的电势,故B错误;
C.根据EP=qφ可知,正电荷在电势高的地方电势能大,所以将带正电的试探电荷从电势低b点移到电势高d点,电场力做负功,电势能增加,故C正确;
D.根据EP=qφ可知,负电荷在电势低的地方电势能大,所以负电荷在电势低的c点的电势能大于在电势高的a点的电势能,故D错误。
故选:C。
【点评】该题结合等势面考查对电场强度理解,知道无论是电场线或是等差等势面,都是密的地方场强大,疏的地方场强小;把握电场强度的矢量性是解该题的关键。
4.(2024春 新吴区校级期末)一匀强电场的方向平行于xOy平面,平面内a、b、c三点的位置如图所示,三点的电势分别为10V、10V、22V。下列说法不正确的是( )
A.电场强度的大小为2.5V/cm
B.坐标原点处的电势为﹣2V
C.电子在a点的电势能比在c点的低12eV
D.电子从b点运动到c点,静电力做功为12eV
【考点】等分法求电势;电场力做功的计算及其特点;电场力做功与电势能变化的关系;匀强电场中电势差与电场强度的关系.
【专题】定量思想;方程法;电场力与电势的性质专题;推理论证能力.
【答案】C
【分析】根据匀强电场中分析坐标原点处的电势,由几何关系求出a、b连线中点的电势。作出电场线,再根据E求电场强度的大小;根据电势能公式EP=qφ求电子在a、c点的电势能之差;根据W=qU求出电场力所做的功。
【解答】解:AB、根据匀强电场中电势差与电场强度的关系式公式U=Ed,知aO间与cb间电势差相等,即φa﹣φO=φc﹣φb,因a、b、c三点电势分别为φa=10V、φb=10V、φc=22V,解得原点处的电势为φ0=﹣2V;
因a、b两点电势相等,所以ab连线是一条等势线,则电场线的方向如图所示:
cb间的电势差:Ucb=φc﹣φb=22V﹣10V=12V
根据几何知识得c点到ab连线的距离:d=ac sin37°=8×0.6cm=4.8cm
则电场强度为:EV/cm=2.5V/cm,故AB正确;
C、电子在a、c点的电势能之差:ΔEp=(﹣eφa)﹣(﹣eφc)=﹣10eV﹣(﹣22eV)=12eV,即电子在a点的电势能比在c点的高12eV,故C错误;
D、bc间的电势差Ubc=10V﹣22V=﹣12V,故电子从b点运动到c点,电场力做功为:W=eUbc=﹣e×(﹣12V)=12eV,故D正确。
本题选错误的,故选:C。
【点评】本题的关键是掌握匀强电场中电势差与电场强度的关系式公式U=Ed,注意正确运用几何关系求解电场强度。要注意公式U=Ed中d是指两点间沿电场方向的距离;同时注意求解电势能和电场力做功时要代入各物理量的符号。
二.多选题(共3小题)
(多选)5.(2024春 大连期末)如图所示,在地面上方的水平匀强电场中,一个质量为m、带正电的电荷量为q的小球,系在一根长为R的绝缘细线的一端,可以在竖直平面内绕O点做圆周运动。AB为圆周的水平直径,CD为竖直直径。已知重力加速度的大小为g,电场强度。
若小球恰能在竖直平面内绕O点做圆周运动,不计空气阻力,则下列说法正确的是( )
A.小球运动到C点时细线的拉力最大
B.小球运动到B点时的电势能最大
C.小球运动到B点时的机械能最大
D.小球运动过程中的最小速度为
【考点】带电粒子(计重力)在匀强电场中的圆周运动;从能量转化与守恒的角度解决电场中的问题.
【专题】定量思想;推理法;带电粒子在电场中的运动专题;分析综合能力.
【答案】CD
【分析】若小球恰能在竖直平面内绕O点做圆周运动,在等效最高点时,细线拉力为零,由重力和电场力的合力提供向心力,由牛顿第二定律求最小速度。根据对称性确定速度最大即动能最大的位置。根据电场力做功情况分析小球机械能最大的位置。根据运动情况确定小球运动到B点的电势能。
【解答】解:AD.带正电的电荷量为q的小球受到的电场力大小为
F=qE
解得
则重力和电场力的合力大小为
解得
F合=2mg
重力和电场力的合力方向与竖直方向的夹角满足
可得
θ=60°
如图所示
可知小球运动等效最低点G时速度最大,细线的拉力最大;小球运动等效最高点H时速度最小,则有
解得小球运动过程中的最小速度为
故A错误,D正确;
BC.从小球从A到B过程,电场力对小球一直做正功,小球电势能减小,小球从B到A过程,电场力对小球一直做负功,小球电势能增大,则小球运动到B点时的电势能最小,小球运动到B点时的机械能最大,故B错误,C正确。
故选:CD。
【点评】解答本题时,要掌握功能关系,注意类比法的应用,小球能够完成圆周运动的条件是丝线的拉力大于或等于零,在最高点的速度最小恰好满足重力与电场力的合力提供向心力。
(多选)6.(2024秋 海淀区期末)某静电场的电势φ在x轴上的分布如图所示,B、C是x轴上关于坐标原点O对称的两点。一个带负电的粒子仅在电场力作用下,以O点为中心、沿x轴方向在B、C两点间做周期性往复运动。下列说法正确的是( )
A.从B运动到C的过程中,电场力先做正功,后做负功
B.从B运动到O的过程中,粒子的加速度先减小后增大
C.粒子在O点的电势能最小
D.粒子的运动是简谐运动
【考点】电场力做功与电势能变化的关系;电势的定义、单位和物理意义及用定义式计算电势;匀强电场中电势差与电场强度的关系.
【专题】定性思想;归纳法;带电粒子在电场中的运动专题;推理论证能力.
【答案】AC
【分析】根据沿电场线方向电势逐渐降低判断O点的电势最高,进而确定电场线的方向,进而判断电场力做功情况,进而判断AC;根据φ﹣x图像的斜率判断电场强的大小,进而根据牛顿第二定律判断B;根据简谐运动的回复力公式判断粒子是否做简谐运动。
【解答】解:AC.根据电场中的规律可知沿电场线方向电势降低,O点处电势最高,则BO段电场的方向沿x轴负方向,OC段电场的方向沿x轴正方向,带负电的粒子在BO段受到向右的电场力的作用,在OC段受到向左的电场力的作用,所以粒子在从B运动到C的过程中,电场力先做正功后做负功,则电势能先减小后增大,在O点电势能最小,故AC正确;
B.根据φ﹣x图像规律可知图线的斜率的绝对值表示电场强度的大小,根据
可知,粒子q、m不变的情况下,从B运动到O的过程中,电场强度的大小先增大后减小,则粒子加速度先增大后减小,故B错误;
D.简谐运动需满足回复力
F=﹣kx
则偏离平衡位置位移越大,物体所受的回复力越大,而根据B选项分析可知往复运动的端点B点和C点处场强不是最大的,则受力不是最大,不符合简谐运动的条件,故D错误。
故选:AC。
【点评】知道φ﹣x的斜率表示电场强度,以及沿电场线方向电势逐渐降低是解题的基础。
(多选)7.(2024春 湖南期末)如图甲所示,粗糙、绝缘的水平地面上,一质量m=1kg的带负电小滑块(可视为质点)在x=1m处以v0=2m/s的初速度沿x轴正方向运动,滑块与地面间的动摩擦因数μ=0.05。在x=0及x=5m处有两个电性未知,电荷量分别为Q1、Q2的点电荷场源,滑块在不同位置所具有的电势能Ep如图乙所示,P点是图线最低点,虚线AB是图像在x=1m处的切线,g=10m/s2下列说法正确的选项是( )
A.滑块在x=3m处所受合外力小于 0.5N
B.两场源电荷均带负电,且|Q1|>|Q2|
C.滑块向右运动过程中,速度始终减小
D.滑块向右一定可以经过x=4m处的位置
【考点】电场力做功与电势能变化的关系;匀强电场中电势差与电场强度的关系.
【专题】比较思想;图析法;电场力与电势的性质专题;理解能力.
【答案】BD
【分析】Ep﹣x图像斜率的绝对值表示滑块所受电场力的大小,确定滑块在x=3m处所受电场力大小,再求合外力大小。在x=3m处电场力为0,电场强度为0,根据点电荷场强公式分析Q1、Q2的电荷量关系。滑块在x=3m处电势能最低,因为滑块带负电,所以x=3m处的电势最高,结合摩擦力可知速度的变化情况;根据能量守恒定律判断滑块是否到达x=4m处的位置。
【解答】解:A、Ep﹣x图像斜率的绝对值表示滑块所受电场力的大小,则知滑块在x=3m处所受电场力为0,所受合外力F合=f=μmg=0.05×1×10N=0.5N,故A错误;
B、滑块在x=3m处所受电场力为0,则该处电场强度为0,则kk,由于r1>r2,所以|Q1|>|Q2|。
滑块在x=3m处电势能最低,因为滑块带负电,所以x=3m处的电势最高,两场源电荷均带负电,故B正确;
C、滑块在x=1m处所受电场力大小为
所以在x=1m处,滑块所受电场力与滑动摩擦力方向相反,且电场力大于摩擦力,则滑块做加速运动,故C错误;
D、滑块在x=1m处的电势能与在x=4m处的电势能相等,根据能量守恒定律,若滑块能够经过x=4m处,则应满足:fΔx=0.5×(4﹣1)J=1.5J
根据题中数据可知实际情况并满足上式,所以滑块一定可以经过x=4m处的位置,故D正确。
故选:BD。
【点评】本题考查电势能与电场力做功,解题关键要掌握电势能与电势的关系,注意Ep﹣x图像斜率的绝对值表示滑块所受电场力的大小。
三.填空题(共4小题)
8.(2024春 东城区校级期末)某同学利用如图所示的实验电路观察平行板电容器的充放电现象。按如图所示电路原理图连接好实验电路,将开关S接在 1 (选填“1”或“2”),可对电容器进行充电。
【考点】观察电容器及其充、放电现象.
【专题】实验题;学科综合题;定性思想;实验分析法;电容器专题;实验探究能力.
【答案】1
【分析】对电容器进行充电时,电容器两端应与电源两端相接。
【解答】解:对电容器进行充电,电容器要与电源串联在电路中,将开关S接在1。
故答案为:1.
【点评】本题为观察电容器的充放电实验对电容器进行充电时,电容器两端应与电源两端相接。
9.(2024春 鼓楼区校级期末)如图所示,xOy坐标系中,A点的坐标为(0,20cm),B点的坐标为(15cm,0),匀强电场的方向平行于坐标系平面,其中坐标原点O处的电势为0V,A点电势为32V,B点电势为﹣18V,则AB中点的电势为 7 V,该电场的电场强度大小为 200 V/m。
【考点】匀强电场中电势差与电场强度的关系.
【专题】定量思想;推理法;电场力与电势的性质专题;分析综合能力.
【答案】7;200
【分析】根据题目信息从图中找到等势面画出等势线,再根据电势差和电场强度关系列式求解。
【解答】解:设AB中点为C,AB中点的电势为
x轴方向的电场强度大小为
y轴方向的电场强度大小为
电场的电场强度大小为
代入数据得E=200V/m
故答案为:7;200
【点评】本题考查电势差和电场强度的关系,比较简单,但是必须正确找到等势面,再画出电场线。
10.(2024春 浦东新区校级期末)若将一个电量为2.0×10﹣10C的正电荷,从零电势点移动到电场中的M点需要克服电场力做功8×10﹣9J,则M点的电势是 40 V;若再将电荷从电场的M点移动到电场中的N点,电场力做功1.8×10﹣8J,则M、N两点间的电势差UMN= 90 V。
【考点】电荷性质、电势能和电势的关系;电场力做功与电势能变化的关系.
【专题】定量思想;推理法;带电粒子在电场中的运动专题;推理论证能力.
【答案】40,90。
【分析】根据电势差的定义式计算两点之间的电势差,然后根据U0M=0﹣φM计算M点的电势。
【解答】解:零电势点和M点的电势差为U0M,根据U0M=0﹣φM可得M点的电势为40V
M、N两点间的电势差UMN
故答案为:40,90。
【点评】掌握电势差的计算公式是解题的基础。
11.(2024春 东城区校级期末)如图甲是某电场中的一条电场线,a、b是这条线上的两点。若将一负点电荷从a点由静止释放,负电荷只受电场力作用,沿电场线从a运动到b。在这过程中,电荷的速度—时间图线如图乙所示。比较a、b两点电势的高低关系是φa < φb,场强的大小关系是Ea = Eb。(选填“>”“<”或“=”)
【考点】电势的定义、单位和物理意义及用定义式计算电势;电场线的定义及基本特征.
【专题】定性思想;推理法;电场力与电势的性质专题;推理论证能力.
【答案】<,=。
【分析】从速度—时间图线得到负电荷做匀加速运动,加速度不变,根据牛顿第二定律得到电场力的变化情况;电势的高低看电场线的指向,沿着电场线电势降低。
【解答】解:负电子从a运动到b,由速度—时间图线得到负电荷做加速运动,故电场力向右;
因为图线的斜率不变,故加速度不变,因此电场力不变,所以电场强度不变,即Ea=Eb;
负电荷受到的电场力与场强方向相反,故场强向左,沿场强方向,电势降低,故b点电势较大,即φa<φb。
故答案为:<,=。
【点评】本题关键通过速度—时间图象得到物体的速度变化情况和加速度变化情况,然后判断场强方向和电势大小。
四.解答题(共4小题)
12.(2024春 天心区校级期末)如图(a),同一竖直平面内A、B、M、N四点距O点的距离均为,O为水平连线AB的中点,M、N在AB连线的中垂线上。A、B两点分别固定有一点电荷,电荷量均为Q(Q>0)。以O为原点,竖直向下为正方向建立x轴。若取无穷远处为电势零点,则ON上的电势φ随位置x的变化关系如图(b)所示。一电荷量为Q(Q>0)的小球S1以一定初动能从M点竖直下落,一段时间后经过N点,其在ON段运动的加速度大小a随位置x的变化关系如图(c)所示。图中g为重力加速度大小,k为静电力常量。
(1)求M点的电场强度;
(2)求小球S1的重力;
(3)为保证S1能运动到N点,S1从M点下落时的初动能须满足什么条件?
【考点】带电粒子(计重力)在非匀强电场中的直线运动;点电荷与均匀带电球体(球壳)周围的电场;电场强度的叠加.
【专题】计算题;定量思想;图析法;动能定理的应用专题;带电粒子在电场中的运动专题;分析综合能力.
【答案】(1)M点的电场强度大小为,方向由O指向M;
(2)小球S1的重力为;
(3)为保证S1能运动到N点,S1从M点下落时的初动能须满足。
【分析】(1)根据点电荷的场强公式结合矢量的合成求解M点的电场强度大小,判断其方向;
(2)根据牛顿第二定律结合力的合成可解得小球S1的重力;
(3)为保证S1能运动到N点与S2相碰,S1运动到D点时的速度必须大于零,根据动能定理确定S1从M点下落时的初动能须满足的条件。
【解答】解:(1)由点电荷场强公式可得,单个点电荷在M点的场强大小为
两个点电荷在M点的电场强度方向垂直,则M点的电场强度为
EME
方向由O指向M。
(2)设O点下方处为C点,A与C的距离为RC,小球S1在C处所受的库仑力大小为FC,由库仑定律和力的合成有
式中
设小球S1的质量为m1,小球S1在C点的加速度大小为a,由牛顿第二定律有
FC+m1g=m1a
由图(c)可知,a=2g
联立并代入数据解得:
(3)设O点上方处为D点。根据图(c)和对称性可知,S1在D点所受的电场力大小等于小球的重力大小,方向竖直向上,S1在此处加速度为0;S1在D点上方做减速运动,在D点下方做加速运动,为保证S1能运动到N点,S1运动到D点时的速度必须大于零
设M点与D点电势差为UMD,由电势差与电势的关系有
UMD=φM﹣φD
设小球S1初动能为Ek,运动到D点的动能为EkD,由动能定理有
m1g(MO﹣DO)+QUMD=EkD﹣Ek
其中EkD>0
由对称性,D点与C点电势相等,M点与N点电势相等,依据图(b)所给数据,联立解得:
即为保证S1能运动到N点,S1从M点下落时的初动能须满足。
答:(1)M点的电场强度大小为,方向由O指向M;
(2)小球S1的重力为;
(3)为保证S1能运动到N点,S1从M点下落时的初动能须满足。
【点评】本题考查牛顿第二定律、动能定理,结合带电粒子在电场中运动的规律,解题关键掌握粒子的运动情况分析,有一定的难度。
13.(2024秋 天心区校级期末)如图,水平地面上放置一长度L=10m、质量M=1kg的长木板。一可视为质点、质量m=1kg、带电量q=+1×10﹣5C的小物块放在木板上,小物块到木板右端距离d1=7m。在距木板右端d2=9m的虚线右侧,存在宽度d3=11.5m的匀强电场,场强E1=2×106N/C,方向竖直向下。匀强电场E1右侧存在宽度,d4=6m的匀强电场,场强E2=1×106N/C,方向竖直向上。从t=0时刻起,水平恒力F=8N作用在长木板上,5s末撤去。已知物块与长木板间的动摩擦因数μ1=0.4,长木板与水平地面间的动摩擦因数μ2=0.2,物块带电量始终不变,重力加速度g取10m/s2,求:
(1)物块运动多长时间进入匀强电场E1;
(2)物块离开匀强电场E2时速度的大小;
(3)物块最终停下来时,离木板右端的距离。
【考点】从能量转化与守恒的角度解决电场中的问题;牛顿第二定律的简单应用.
【专题】定量思想;推理法;带电粒子在电场中的运动专题;分析综合能力.
【答案】(1)物块运动4s进入匀强电场E1;
(2)物块离开匀强电场E2时速度的大小6m/s;
(3)物块最终停下来时,离木板右端的距离5.5m。
【分析】(1)根据牛顿第二定律求出物块的加速度,结合题设条件确定物块和木板的运动状态,求得物块运动多长时间进入匀强电场;
(2)(3)由运动学规律进入电场的位移,进入电场后根据动力学规律物块的运动过程,再结合题设条件求物块离开匀强电场E2时速度的大小,物块最终停下来时,离木板右端的距离。
【解答】解:(1)在物块未进入电场时设其最大加速度大小为a0,则由牛顿第二定律有
μ1mg=ma0
解得
当给木板施加恒力时,假设物块和木板能够保持相对静止,一起做匀加速直线运动,设共同加速度的加速度大小为a,则对整体由牛顿第二定律有
F﹣μ2(m+M)g=(m+M)a
代入数据解得
a=2m/s2<a0
则假设成立,在未撤去力F的时间内物块的位移
可知
x0>d1+d2
则可知在力F撤去前的某一时间内物块已经进入电场,设从开始运动到物块进入电场的施加为t0,由位移与时间的关系可得
解得
t0=4s
(2)当物块进入电场E1后由于电场力竖直向下,增加了物块对木板的正压力同时也增加了木板对地面的正压力,因此可知木块仍相对于木板静止,在电场E1中,在力F未撤去时,设物块和木板共同运动的加速度大小为a1,由牛顿第二定律有
F﹣μ2[(m+M)g+Eq]=(m+M)a1
解得
a1=0
即在物块进入电场E1中的1s时间内物块和木板一起做匀速直线运动,设其位移为x1,进入电场E1时的速度大小为v1,则有
v1=at0=2×4m/s=8m/s
x1=v1t1=8×1m=8m
此时距进入电场E2的距离为
x2=d3﹣x1=11.5m﹣8m=3.5m
设在这段位移内物块和木板共同运动的加速度大小为a′1,由牛顿第二定律有
μ2[(m+M)g+Eq]=(m+M)a′1
解得
设物块和木板共同进入电场E2时的速度大小为v2,则由速度与位移的关系可得
解得
v2=6m/s
当进入匀强电场E2,电场力竖直向上,对物块在竖直方向有
mg=E2q
可知,物块在电场E2中做匀速直线运动,因此,物块离开匀强电场E2时速度的大小为6m/s。
(3)设物块出电场E2所用的时间为t2,在物块出电场E2的过程中木板在电场E2中做匀减速直线运动的加速度大小为a2,则有
d4=v2t2
μ2Mg=Ma2
解得
t2=1s,
设该过程中木板的位移为x3,可得
解得
x3=5m
则可得物块出电场E2时距离木板右端的距离为
d5=d1﹣(d4﹣x3)
解得
d5=6m
此时木板的速度
v3=v2﹣a2t2
解得
v3=4m/s
此后在两者达到共速前物块的加速度大小为,设木板的加速度大小为a3,对木板由牛顿第二定律有
μ1mg﹣μ2(m+M)g=Ma3
解得
a3=0
即物块出电场E2后做匀减速直线运动,而木板做匀速直线运动,设达到共速所用时间为t3,根据速度—时间关系可得
v3=v2﹣a0t3
解得
t3=0.5s
则在该时间内物块和木板的位移分别为x4、x5,则根据位移与时间的关系有
x5=v3t3=4×0.5m=2m
两者达到共速后将一起做减速运动,直至停止,则可知物块最终离木板右端的距离为
d6=d5﹣(x4﹣x5)
解得
d6=5.5m
答:(1)物块运动4s进入匀强电场E1;
(2)物块离开匀强电场E2时速度的大小6m/s;
(3)物块最终停下来时,离木板右端的距离5.5m。
【点评】本题难度较大,这是一道涉及电场的在水平面上的有拉力的板块模型,一定要分清两个物体的运动状态,用动力学规律可以解决相应的问题。
14.(2024秋 厦门期末)如图甲所示,一倾角为30°足够长的绝缘斜面固定在水平地面上,质量为m、电荷量为﹣q(q>0)的物块A压缩轻质绝缘微型弹簧a后锁定(A与弹簧不拴接)。空间中存在沿斜面向上、大小E(g为重力加速度)的匀强电场。质量为2m、电荷量为+q的物块B静止在斜面上端,B左侧固定有处于原长的轻质绝缘弹簧b,A、B与斜面的滑动摩擦力大小分别为mg、mg,最大静摩擦力等于滑动摩擦力。
t=0时解除锁定,弹簧的弹性势能Ep瞬间全部转化为A的动能,A运动距离L后于t1时刻到达P点,此时速度为v1、加速度为0,且未与弹簧b接触;t2时刻,A到达Q点,速度达到最大值2v1,弹簧b的弹力大小为mg,此过程中A的v﹣t图像如图乙所示。已知A、B的电荷量始终保持不变,两者间的库仑力等效为真空中点电荷间的静电力,静电力常量为k,弹簧始终在弹性限度内。求:
(1)弹射过程弹簧a对A冲量的大小;
(2)A从开始运动到P点的过程中,B对A库仑力所做的功;
(3)A到达P点时,A与B之间的距离;
(4)A从P点运动到Q点的过程中,A、B系统(含弹簧b)的电势能变化量与弹性势能变化量的总和。
【考点】从能量转化与守恒的角度解决电场中的问题;动能定理的简单应用;常见力做功与相应的能量转化;动量定理的内容和应用;电场力做功与电势能变化的关系.
【专题】定量思想;方程法;带电粒子在复合场中的运动专题;分析综合能力.
【答案】(1)弹射过程弹簧a对A冲量的大小为;
(2)A从开始运动到P点的过程中,B对A库仑力所做的功为mgLEp;
(3)A到达P点时,A与B之间的距离为;
(4)A从P点运动到Q点的过程中,A、B系统(含弹簧b)的电势能变化量与弹性势能变化量的总和为。
【分析】(1)物块A压缩轻质绝缘微型弹簧a,弹簧的弹性势能Ep瞬间全部转化为A的动能,根据动能定理和动量定理求解;
(2)从A从开始运动到P点的过程中,根据动能定理求解B对A库仑力所做的功;
(3)A到达P点时,A的加速度为零,根据平衡条件进行解答;
(4)物块A在P点时,对B分析,分析B的受力情况和运动情况;以A和B整体为研究对象,根据动量守恒定律求解B的速度大小;滑块A在Q点时,二者之间的距离为x′,对A根据平衡条件求解A的位移,由此得到B的位移大小,对系统,根据能量守恒定律、功能关系可得A、B系统(含弹簧b)的电势能变化量与弹性势能变化量的总和。
【解答】解:(1)物块A压缩轻质绝缘微型弹簧a,弹簧的弹性势能Ep瞬间全部转化为A的动能,则有:Ep
解得:v
取沿斜面向上为正方向,根据动量定理可得弹射过程弹簧a对A冲量的大小为:I=mv﹣0=m;
(2)从A从开始运动到P点的过程中,根据动能定理可得:WBA﹣mgLsin30°mgL﹣qEL
解得B对A库仑力所做的功:WBAmgLEp;
(3)A到达P点时,A的加速度为零,则有:mgsin30°﹣qEmg=0
解得A与B之间的距离:x;
(4)物块A在P点时,对B分析,设此次B的摩擦力大小为f,则有:f2mgsin30°﹣qE
解得:f
此时B的摩擦力达到最大,此后A向上运动过程中,B向下运动。
以A和B整体为研究对象,合外力为:F合=3mgsin30°mgmg=0
说明A从P到Q运动过程中,系统合外力为零,则动量守恒;当A到Q点时,设B的速度大小为vB,取沿斜面向上为正方向,根据动量守恒定律可得:
mv1=m 2v1+2mvB
解得:vBv1
滑块A在Q点时,二者之间的距离为x′,对A根据平衡条件有:mg﹣mgsin30°﹣qEmg=0
解得:x′
由于A和B的合外力大小相等,而B的质量为A的质量的2倍,则B的加速度始终为A的一半,则A的位移等于B的位移的2倍。
则从A从P到Q过程中,二者的位移之和位移为:xA+xB=x﹣x′
B的位移为:xB()
对系统,根据能量守恒定律可得:W电场力+W弹簧+2mgxBsin30°﹣mgxAsin30°mgxAmgxB
解得:W电场力+W弹簧
根据功能关系可得A、B系统(含弹簧b)的电势能变化量与弹性势能变化量的总和:ΔEP=﹣W电场力+W弹簧
则ΔEp。
答:(1)弹射过程弹簧a对A冲量的大小为;
(2)A从开始运动到P点的过程中,B对A库仑力所做的功为mgLEp;
(3)A到达P点时,A与B之间的距离为;
(4)A从P点运动到Q点的过程中,A、B系统(含弹簧b)的电势能变化量与弹性势能变化量的总和为。
【点评】本题主要是考查带电物块在电场中的运动,关键是弄清楚物块的受力情况和运动情况,结合动能定理、功能关系进行解答。
15.(2024春 宿州期末)如图所示,由电子枪发出的电子从静止开始经加速电场加速后,沿平行于板面的方向射入偏转电场,并从另一侧射出。已知电子质量为m,电荷量为e,加速电场电压为U0,偏转电场可视为匀强电场,偏转电极YY'之间电压为U,极板长度为L,两极板间距离为d。不计电子重力和电子间相互作用,求:
(1)电子离开加速电场时的速度大小v0;
(2)电子在偏转电场中的加速度大小a;
(3)电子从偏转电场射出时沿垂直板面方向的偏转距离y。
【考点】从能量转化与守恒的角度解决电场中的问题.
【专题】计算题;定量思想;推理法;带电粒子在电场中的运动专题.
【答案】见试题解答内容
【分析】(1)在加速电场中动能定理可求出电子离开电场的速度;
(2)在偏转电场中,由牛顿第二定律可求出加速度大小;
(3)在偏转电场中,电子做类平抛运动,根据平抛运动的规律求出竖直方向的位移y。
【解答】解:(1)在加速电场中,由动能定理可知:eU0
解得:v0
(2)电子在偏转电场中,竖直方向只受电场力作用,由牛顿第二定律可知:
F=ma
F=eE=e
解得:a
(3)电子在偏转电场中做类平抛运动,
水平方向:L=v0t
竖直方向:yat2
联立解得:y
答:(1)电子离开加速电场时的速度大小v0为;
(2)电子在偏转电场中的加速度大小a为;
(3)电子从偏转电场射出时沿垂直板面方向的偏转距离y为。
【点评】本题考查带电粒子在加速电场和偏转电场中的运动,在加速电场中动能定理求末速度;
在偏转电场中做类平抛运动,根据平抛运动的规律求出相关物理量。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.夯实基础 静电场中的能量
一.选择题(共4小题)
1.(2024秋 锡山区校级期末)两个点电荷,电性未知、电荷量大小分别为4q和q,其电场线如图所示(未标明方向,且未画出对称轴附近的电场线),A、B、C、D为对称轴上的四个点,且满足AB=BC=CD,则( )
A.A、D两点的场强方向一定相反
B.从D点向左至无穷远,场强不断减小
C.若电荷量为4q的点电荷为负电荷,则电子从A向B移动的过程中,电势能减小
D.若电荷量为4q的点电荷为负电荷,则A点电势低于D点电势
2.(2024秋 朝阳区期末)有人认为在两个带电导体之间可以存在如图所示的静电场,它的电场线相互平行,间距不等。关于此“静电场”,下列说法正确的是( )
A.该电场一定存在,是个特殊的匀强电场
B.该电场一定存在,可以通过两个匀强电场叠加产生
C.根据图中a、b两点电场强度方向相同,大小不同,可判断该电场不存在
D.通过试探电荷沿不同路径从图中a点移动到b点,电场力做功不同,可判断该电场不存在
3.(2024秋 大连期末)有研究表明,当兴奋情绪传播时,在人的体表可以测出与之对应的电势变化。某一瞬间人体表面的电势分布图如图所示,图中实线为等差等势面,标在等势面上的数值分别表示该等势面的电势,a、b、c、d为等势面上的点,该电场可等效为两等量异种电荷产生的电场,a、b为两电荷连线上对称的两点,c、d为两电荷连线中垂线上对称的两点。下列说法中正确的是( )
A.a、b两点的电场强度大小相等,方向相反
B.c点的电势大于d点的电势
C.将带正电的试探电荷从b点移到d点,电场力做负功
D.负电荷在c点的电势能小于在a点的电势能
4.(2024春 新吴区校级期末)一匀强电场的方向平行于xOy平面,平面内a、b、c三点的位置如图所示,三点的电势分别为10V、10V、22V。下列说法不正确的是( )
A.电场强度的大小为2.5V/cm
B.坐标原点处的电势为﹣2V
C.电子在a点的电势能比在c点的低12eV
D.电子从b点运动到c点,静电力做功为12eV
二.多选题(共3小题)
(多选)5.(2024春 大连期末)如图所示,在地面上方的水平匀强电场中,一个质量为m、带正电的电荷量为q的小球,系在一根长为R的绝缘细线的一端,可以在竖直平面内绕O点做圆周运动。AB为圆周的水平直径,CD为竖直直径。已知重力加速度的大小为g,电场强度。
若小球恰能在竖直平面内绕O点做圆周运动,不计空气阻力,则下列说法正确的是( )
A.小球运动到C点时细线的拉力最大
B.小球运动到B点时的电势能最大
C.小球运动到B点时的机械能最大
D.小球运动过程中的最小速度为
(多选)6.(2024秋 海淀区期末)某静电场的电势φ在x轴上的分布如图所示,B、C是x轴上关于坐标原点O对称的两点。一个带负电的粒子仅在电场力作用下,以O点为中心、沿x轴方向在B、C两点间做周期性往复运动。下列说法正确的是( )
A.从B运动到C的过程中,电场力先做正功,后做负功
B.从B运动到O的过程中,粒子的加速度先减小后增大
C.粒子在O点的电势能最小
D.粒子的运动是简谐运动
(多选)7.(2024春 湖南期末)如图甲所示,粗糙、绝缘的水平地面上,一质量m=1kg的带负电小滑块(可视为质点)在x=1m处以v0=2m/s的初速度沿x轴正方向运动,滑块与地面间的动摩擦因数μ=0.05。在x=0及x=5m处有两个电性未知,电荷量分别为Q1、Q2的点电荷场源,滑块在不同位置所具有的电势能Ep如图乙所示,P点是图线最低点,虚线AB是图像在x=1m处的切线,g=10m/s2下列说法正确的选项是( )
A.滑块在x=3m处所受合外力小于 0.5N
B.两场源电荷均带负电,且|Q1|>|Q2|
C.滑块向右运动过程中,速度始终减小
D.滑块向右一定可以经过x=4m处的位置
三.填空题(共4小题)
8.(2024春 东城区校级期末)某同学利用如图所示的实验电路观察平行板电容器的充放电现象。按如图所示电路原理图连接好实验电路,将开关S接在 (选填“1”或“2”),可对电容器进行充电。
9.(2024春 鼓楼区校级期末)如图所示,xOy坐标系中,A点的坐标为(0,20cm),B点的坐标为(15cm,0),匀强电场的方向平行于坐标系平面,其中坐标原点O处的电势为0V,A点电势为32V,B点电势为﹣18V,则AB中点的电势为 V,该电场的电场强度大小为 V/m。
10.(2024春 浦东新区校级期末)若将一个电量为2.0×10﹣10C的正电荷,从零电势点移动到电场中的M点需要克服电场力做功8×10﹣9J,则M点的电势是 V;若再将电荷从电场的M点移动到电场中的N点,电场力做功1.8×10﹣8J,则M、N两点间的电势差UMN= V。
11.(2024春 东城区校级期末)如图甲是某电场中的一条电场线,a、b是这条线上的两点。若将一负点电荷从a点由静止释放,负电荷只受电场力作用,沿电场线从a运动到b。在这过程中,电荷的速度—时间图线如图乙所示。比较a、b两点电势的高低关系是φa φb,场强的大小关系是Ea Eb。(选填“>”“<”或“=”)
四.解答题(共4小题)
12.(2024春 天心区校级期末)如图(a),同一竖直平面内A、B、M、N四点距O点的距离均为,O为水平连线AB的中点,M、N在AB连线的中垂线上。A、B两点分别固定有一点电荷,电荷量均为Q(Q>0)。以O为原点,竖直向下为正方向建立x轴。若取无穷远处为电势零点,则ON上的电势φ随位置x的变化关系如图(b)所示。一电荷量为Q(Q>0)的小球S1以一定初动能从M点竖直下落,一段时间后经过N点,其在ON段运动的加速度大小a随位置x的变化关系如图(c)所示。图中g为重力加速度大小,k为静电力常量。
(1)求M点的电场强度;
(2)求小球S1的重力;
(3)为保证S1能运动到N点,S1从M点下落时的初动能须满足什么条件?
13.(2024秋 天心区校级期末)如图,水平地面上放置一长度L=10m、质量M=1kg的长木板。一可视为质点、质量m=1kg、带电量q=+1×10﹣5C的小物块放在木板上,小物块到木板右端距离d1=7m。在距木板右端d2=9m的虚线右侧,存在宽度d3=11.5m的匀强电场,场强E1=2×106N/C,方向竖直向下。匀强电场E1右侧存在宽度,d4=6m的匀强电场,场强E2=1×106N/C,方向竖直向上。从t=0时刻起,水平恒力F=8N作用在长木板上,5s末撤去。已知物块与长木板间的动摩擦因数μ1=0.4,长木板与水平地面间的动摩擦因数μ2=0.2,物块带电量始终不变,重力加速度g取10m/s2,求:
(1)物块运动多长时间进入匀强电场E1;
(2)物块离开匀强电场E2时速度的大小;
(3)物块最终停下来时,离木板右端的距离。
14.(2024秋 厦门期末)如图甲所示,一倾角为30°足够长的绝缘斜面固定在水平地面上,质量为m、电荷量为﹣q(q>0)的物块A压缩轻质绝缘微型弹簧a后锁定(A与弹簧不拴接)。空间中存在沿斜面向上、大小E(g为重力加速度)的匀强电场。质量为2m、电荷量为+q的物块B静止在斜面上端,B左侧固定有处于原长的轻质绝缘弹簧b,A、B与斜面的滑动摩擦力大小分别为mg、mg,最大静摩擦力等于滑动摩擦力。
t=0时解除锁定,弹簧的弹性势能Ep瞬间全部转化为A的动能,A运动距离L后于t1时刻到达P点,此时速度为v1、加速度为0,且未与弹簧b接触;t2时刻,A到达Q点,速度达到最大值2v1,弹簧b的弹力大小为mg,此过程中A的v﹣t图像如图乙所示。已知A、B的电荷量始终保持不变,两者间的库仑力等效为真空中点电荷间的静电力,静电力常量为k,弹簧始终在弹性限度内。求:
(1)弹射过程弹簧a对A冲量的大小;
(2)A从开始运动到P点的过程中,B对A库仑力所做的功;
(3)A到达P点时,A与B之间的距离;
(4)A从P点运动到Q点的过程中,A、B系统(含弹簧b)的电势能变化量与弹性势能变化量的总和。
15.(2024春 宿州期末)如图所示,由电子枪发出的电子从静止开始经加速电场加速后,沿平行于板面的方向射入偏转电场,并从另一侧射出。已知电子质量为m,电荷量为e,加速电场电压为U0,偏转电场可视为匀强电场,偏转电极YY'之间电压为U,极板长度为L,两极板间距离为d。不计电子重力和电子间相互作用,求:
(1)电子离开加速电场时的速度大小v0;
(2)电子在偏转电场中的加速度大小a;
(3)电子从偏转电场射出时沿垂直板面方向的偏转距离y。
预习衔接.夯实基础 静电场中的能量
参考答案与试题解析
一.选择题(共4小题)
1.(2024秋 锡山区校级期末)两个点电荷,电性未知、电荷量大小分别为4q和q,其电场线如图所示(未标明方向,且未画出对称轴附近的电场线),A、B、C、D为对称轴上的四个点,且满足AB=BC=CD,则( )
A.A、D两点的场强方向一定相反
B.从D点向左至无穷远,场强不断减小
C.若电荷量为4q的点电荷为负电荷,则电子从A向B移动的过程中,电势能减小
D.若电荷量为4q的点电荷为负电荷,则A点电势低于D点电势
【考点】电场力做功与电势能变化的关系;电势的定义、单位和物理意义及用定义式计算电势;电场线的定义及基本特征.
【专题】比较思想;图析法;电场力与电势的性质专题;理解能力.
【答案】D
【分析】根据点电荷场强公式E=k和电场的叠加原理确定A、D两点的场强方向关系,并分析场强的变化情况;根据电场力做功情况判断电势能的变化情况;根据离正点电荷越近电势越高,离负点电荷越近电势越低,分析A点与D点电势高低。
【解答】解:AB、由图中电场线分布情况可知,两点电荷为异种电荷,且B处电场线密,则B处电荷量为4q,C处电荷量为q。设电荷量为4q的点电荷为负电荷,电荷量为q的点电荷为正电荷,并设AB=BC=CD=r,则A点的场强大小为,(方向指向负点电荷4q),D点的场强大小为。
由于D点的场强大小为零,无穷远处场强也为零,所以从D点向左至无穷远,场强先增大后减小,故AB错误;
C、若电荷量为4q的点电荷为负电荷,电子从A向B移动的过程中,场强方向由A指向B,电子所受的电场力与运动方向相反,电场力对电子做负功,所以电子的电势能增加,故C错误;
D、若电荷量为4q的点电荷为负电荷,则B处为4q负电荷,C处q为正电荷,根据离正点电荷越近电势越高,离负点电荷越近电势越低,则知﹣4q点电荷在A点的电势低于D点电势,+q点电荷在A点的电势低于D点电势,由电场的叠加原理可知,A点电势低于D点电势,故D正确。
故选:D。
【点评】解答本题的关键要掌握电场的叠加原理,根据场强的合成分析合场强的方向,判断电场力做功情况,从而分析电势能的变化情况。
2.(2024秋 朝阳区期末)有人认为在两个带电导体之间可以存在如图所示的静电场,它的电场线相互平行,间距不等。关于此“静电场”,下列说法正确的是( )
A.该电场一定存在,是个特殊的匀强电场
B.该电场一定存在,可以通过两个匀强电场叠加产生
C.根据图中a、b两点电场强度方向相同,大小不同,可判断该电场不存在
D.通过试探电荷沿不同路径从图中a点移动到b点,电场力做功不同,可判断该电场不存在
【考点】电场力做功与电势能变化的关系;电场线的定义及基本特征.
【专题】定性思想;极端假设法;电场力与电势的性质专题;推理论证能力.
【答案】D
【分析】根据匀强电场的特点判断AB;根据等势面的特点和电势差与场强的关系判断C;根据电场力做功特点判断D。
【解答】解:A.电场线相互平行,说明电场中各点的场强方向相同,而电场线间距不等说明电场中各点场强大小不是处处相等,不是匀强电场,故A错误;
B.将两个匀强电场叠加,获得的电场仍为匀强电场,故B错误;
C:如果存在这样的电场,根据等势面的特点,它的等势面ac、bd应该如下图所示
a、d两点的电势差Uad应该等于c、b两点的电势差Ucb,即
Uad=Ucb
从图中可以看出,a、d两点的距离等于c、b两点的距离,ad处的场强大于cb处的场强。根据
U=Ed
可得
Uad>Ucb
所以这样的电场不可能存在,但等势面上各点的场强不一定大小相等,故C错误;
D.如下图所示
粒子沿两个不同的路径,从a→d→b和从a→c→b,电场力做功不相同(Uad>Ucb),即电场力做功与路径有关,违背了静电场的基本性质,所以这样的电场不可能存在,故D正确。
故选:D。
【点评】知道电场力做功与其路径无关,只与初末位置的电势差有关是解题的关键,另外掌握匀强电场的特点是解题的基础。
3.(2024秋 大连期末)有研究表明,当兴奋情绪传播时,在人的体表可以测出与之对应的电势变化。某一瞬间人体表面的电势分布图如图所示,图中实线为等差等势面,标在等势面上的数值分别表示该等势面的电势,a、b、c、d为等势面上的点,该电场可等效为两等量异种电荷产生的电场,a、b为两电荷连线上对称的两点,c、d为两电荷连线中垂线上对称的两点。下列说法中正确的是( )
A.a、b两点的电场强度大小相等,方向相反
B.c点的电势大于d点的电势
C.将带正电的试探电荷从b点移到d点,电场力做负功
D.负电荷在c点的电势能小于在a点的电势能
【考点】等势面及其与电场线的关系;电场力做功与电势能变化的关系;电势的定义、单位和物理意义及用定义式计算电势.
【专题】定性思想;推理法;电场力与电势的性质专题;理解能力.
【答案】C
【分析】根据等量异种电荷的电场线分布进行分析;根据电势的大小求解ab两点、bc两点的电势差。
【解答】解:A.该电势分布图可等效为等量异种电荷产生的,a、b为两电荷连线上对称的两点,根据等量异种电荷的电场的特点,可以判断、这两个对称点的电场强度大小相等、方向相同,故A错误;
B.c、d两点位于等量异种点电荷连线的中垂线上,该中垂线是一条等势线,则c点的电势等于d点的电势,故B错误;
C.根据EP=qφ可知,正电荷在电势高的地方电势能大,所以将带正电的试探电荷从电势低b点移到电势高d点,电场力做负功,电势能增加,故C正确;
D.根据EP=qφ可知,负电荷在电势低的地方电势能大,所以负电荷在电势低的c点的电势能大于在电势高的a点的电势能,故D错误。
故选:C。
【点评】该题结合等势面考查对电场强度理解,知道无论是电场线或是等差等势面,都是密的地方场强大,疏的地方场强小;把握电场强度的矢量性是解该题的关键。
4.(2024春 新吴区校级期末)一匀强电场的方向平行于xOy平面,平面内a、b、c三点的位置如图所示,三点的电势分别为10V、10V、22V。下列说法不正确的是( )
A.电场强度的大小为2.5V/cm
B.坐标原点处的电势为﹣2V
C.电子在a点的电势能比在c点的低12eV
D.电子从b点运动到c点,静电力做功为12eV
【考点】等分法求电势;电场力做功的计算及其特点;电场力做功与电势能变化的关系;匀强电场中电势差与电场强度的关系.
【专题】定量思想;方程法;电场力与电势的性质专题;推理论证能力.
【答案】C
【分析】根据匀强电场中分析坐标原点处的电势,由几何关系求出a、b连线中点的电势。作出电场线,再根据E求电场强度的大小;根据电势能公式EP=qφ求电子在a、c点的电势能之差;根据W=qU求出电场力所做的功。
【解答】解:AB、根据匀强电场中电势差与电场强度的关系式公式U=Ed,知aO间与cb间电势差相等,即φa﹣φO=φc﹣φb,因a、b、c三点电势分别为φa=10V、φb=10V、φc=22V,解得原点处的电势为φ0=﹣2V;
因a、b两点电势相等,所以ab连线是一条等势线,则电场线的方向如图所示:
cb间的电势差:Ucb=φc﹣φb=22V﹣10V=12V
根据几何知识得c点到ab连线的距离:d=ac sin37°=8×0.6cm=4.8cm
则电场强度为:EV/cm=2.5V/cm,故AB正确;
C、电子在a、c点的电势能之差:ΔEp=(﹣eφa)﹣(﹣eφc)=﹣10eV﹣(﹣22eV)=12eV,即电子在a点的电势能比在c点的高12eV,故C错误;
D、bc间的电势差Ubc=10V﹣22V=﹣12V,故电子从b点运动到c点,电场力做功为:W=eUbc=﹣e×(﹣12V)=12eV,故D正确。
本题选错误的,故选:C。
【点评】本题的关键是掌握匀强电场中电势差与电场强度的关系式公式U=Ed,注意正确运用几何关系求解电场强度。要注意公式U=Ed中d是指两点间沿电场方向的距离;同时注意求解电势能和电场力做功时要代入各物理量的符号。
二.多选题(共3小题)
(多选)5.(2024春 大连期末)如图所示,在地面上方的水平匀强电场中,一个质量为m、带正电的电荷量为q的小球,系在一根长为R的绝缘细线的一端,可以在竖直平面内绕O点做圆周运动。AB为圆周的水平直径,CD为竖直直径。已知重力加速度的大小为g,电场强度。
若小球恰能在竖直平面内绕O点做圆周运动,不计空气阻力,则下列说法正确的是( )
A.小球运动到C点时细线的拉力最大
B.小球运动到B点时的电势能最大
C.小球运动到B点时的机械能最大
D.小球运动过程中的最小速度为
【考点】带电粒子(计重力)在匀强电场中的圆周运动;从能量转化与守恒的角度解决电场中的问题.
【专题】定量思想;推理法;带电粒子在电场中的运动专题;分析综合能力.
【答案】CD
【分析】若小球恰能在竖直平面内绕O点做圆周运动,在等效最高点时,细线拉力为零,由重力和电场力的合力提供向心力,由牛顿第二定律求最小速度。根据对称性确定速度最大即动能最大的位置。根据电场力做功情况分析小球机械能最大的位置。根据运动情况确定小球运动到B点的电势能。
【解答】解:AD.带正电的电荷量为q的小球受到的电场力大小为
F=qE
解得
则重力和电场力的合力大小为
解得
F合=2mg
重力和电场力的合力方向与竖直方向的夹角满足
可得
θ=60°
如图所示
可知小球运动等效最低点G时速度最大,细线的拉力最大;小球运动等效最高点H时速度最小,则有
解得小球运动过程中的最小速度为
故A错误,D正确;
BC.从小球从A到B过程,电场力对小球一直做正功,小球电势能减小,小球从B到A过程,电场力对小球一直做负功,小球电势能增大,则小球运动到B点时的电势能最小,小球运动到B点时的机械能最大,故B错误,C正确。
故选:CD。
【点评】解答本题时,要掌握功能关系,注意类比法的应用,小球能够完成圆周运动的条件是丝线的拉力大于或等于零,在最高点的速度最小恰好满足重力与电场力的合力提供向心力。
(多选)6.(2024秋 海淀区期末)某静电场的电势φ在x轴上的分布如图所示,B、C是x轴上关于坐标原点O对称的两点。一个带负电的粒子仅在电场力作用下,以O点为中心、沿x轴方向在B、C两点间做周期性往复运动。下列说法正确的是( )
A.从B运动到C的过程中,电场力先做正功,后做负功
B.从B运动到O的过程中,粒子的加速度先减小后增大
C.粒子在O点的电势能最小
D.粒子的运动是简谐运动
【考点】电场力做功与电势能变化的关系;电势的定义、单位和物理意义及用定义式计算电势;匀强电场中电势差与电场强度的关系.
【专题】定性思想;归纳法;带电粒子在电场中的运动专题;推理论证能力.
【答案】AC
【分析】根据沿电场线方向电势逐渐降低判断O点的电势最高,进而确定电场线的方向,进而判断电场力做功情况,进而判断AC;根据φ﹣x图像的斜率判断电场强的大小,进而根据牛顿第二定律判断B;根据简谐运动的回复力公式判断粒子是否做简谐运动。
【解答】解:AC.根据电场中的规律可知沿电场线方向电势降低,O点处电势最高,则BO段电场的方向沿x轴负方向,OC段电场的方向沿x轴正方向,带负电的粒子在BO段受到向右的电场力的作用,在OC段受到向左的电场力的作用,所以粒子在从B运动到C的过程中,电场力先做正功后做负功,则电势能先减小后增大,在O点电势能最小,故AC正确;
B.根据φ﹣x图像规律可知图线的斜率的绝对值表示电场强度的大小,根据
可知,粒子q、m不变的情况下,从B运动到O的过程中,电场强度的大小先增大后减小,则粒子加速度先增大后减小,故B错误;
D.简谐运动需满足回复力
F=﹣kx
则偏离平衡位置位移越大,物体所受的回复力越大,而根据B选项分析可知往复运动的端点B点和C点处场强不是最大的,则受力不是最大,不符合简谐运动的条件,故D错误。
故选:AC。
【点评】知道φ﹣x的斜率表示电场强度,以及沿电场线方向电势逐渐降低是解题的基础。
(多选)7.(2024春 湖南期末)如图甲所示,粗糙、绝缘的水平地面上,一质量m=1kg的带负电小滑块(可视为质点)在x=1m处以v0=2m/s的初速度沿x轴正方向运动,滑块与地面间的动摩擦因数μ=0.05。在x=0及x=5m处有两个电性未知,电荷量分别为Q1、Q2的点电荷场源,滑块在不同位置所具有的电势能Ep如图乙所示,P点是图线最低点,虚线AB是图像在x=1m处的切线,g=10m/s2下列说法正确的选项是( )
A.滑块在x=3m处所受合外力小于 0.5N
B.两场源电荷均带负电,且|Q1|>|Q2|
C.滑块向右运动过程中,速度始终减小
D.滑块向右一定可以经过x=4m处的位置
【考点】电场力做功与电势能变化的关系;匀强电场中电势差与电场强度的关系.
【专题】比较思想;图析法;电场力与电势的性质专题;理解能力.
【答案】BD
【分析】Ep﹣x图像斜率的绝对值表示滑块所受电场力的大小,确定滑块在x=3m处所受电场力大小,再求合外力大小。在x=3m处电场力为0,电场强度为0,根据点电荷场强公式分析Q1、Q2的电荷量关系。滑块在x=3m处电势能最低,因为滑块带负电,所以x=3m处的电势最高,结合摩擦力可知速度的变化情况;根据能量守恒定律判断滑块是否到达x=4m处的位置。
【解答】解:A、Ep﹣x图像斜率的绝对值表示滑块所受电场力的大小,则知滑块在x=3m处所受电场力为0,所受合外力F合=f=μmg=0.05×1×10N=0.5N,故A错误;
B、滑块在x=3m处所受电场力为0,则该处电场强度为0,则kk,由于r1>r2,所以|Q1|>|Q2|。
滑块在x=3m处电势能最低,因为滑块带负电,所以x=3m处的电势最高,两场源电荷均带负电,故B正确;
C、滑块在x=1m处所受电场力大小为
所以在x=1m处,滑块所受电场力与滑动摩擦力方向相反,且电场力大于摩擦力,则滑块做加速运动,故C错误;
D、滑块在x=1m处的电势能与在x=4m处的电势能相等,根据能量守恒定律,若滑块能够经过x=4m处,则应满足:fΔx=0.5×(4﹣1)J=1.5J
根据题中数据可知实际情况并满足上式,所以滑块一定可以经过x=4m处的位置,故D正确。
故选:BD。
【点评】本题考查电势能与电场力做功,解题关键要掌握电势能与电势的关系,注意Ep﹣x图像斜率的绝对值表示滑块所受电场力的大小。
三.填空题(共4小题)
8.(2024春 东城区校级期末)某同学利用如图所示的实验电路观察平行板电容器的充放电现象。按如图所示电路原理图连接好实验电路,将开关S接在 1 (选填“1”或“2”),可对电容器进行充电。
【考点】观察电容器及其充、放电现象.
【专题】实验题;学科综合题;定性思想;实验分析法;电容器专题;实验探究能力.
【答案】1
【分析】对电容器进行充电时,电容器两端应与电源两端相接。
【解答】解:对电容器进行充电,电容器要与电源串联在电路中,将开关S接在1。
故答案为:1.
【点评】本题为观察电容器的充放电实验对电容器进行充电时,电容器两端应与电源两端相接。
9.(2024春 鼓楼区校级期末)如图所示,xOy坐标系中,A点的坐标为(0,20cm),B点的坐标为(15cm,0),匀强电场的方向平行于坐标系平面,其中坐标原点O处的电势为0V,A点电势为32V,B点电势为﹣18V,则AB中点的电势为 7 V,该电场的电场强度大小为 200 V/m。
【考点】匀强电场中电势差与电场强度的关系.
【专题】定量思想;推理法;电场力与电势的性质专题;分析综合能力.
【答案】7;200
【分析】根据题目信息从图中找到等势面画出等势线,再根据电势差和电场强度关系列式求解。
【解答】解:设AB中点为C,AB中点的电势为
x轴方向的电场强度大小为
y轴方向的电场强度大小为
电场的电场强度大小为
代入数据得E=200V/m
故答案为:7;200
【点评】本题考查电势差和电场强度的关系,比较简单,但是必须正确找到等势面,再画出电场线。
10.(2024春 浦东新区校级期末)若将一个电量为2.0×10﹣10C的正电荷,从零电势点移动到电场中的M点需要克服电场力做功8×10﹣9J,则M点的电势是 40 V;若再将电荷从电场的M点移动到电场中的N点,电场力做功1.8×10﹣8J,则M、N两点间的电势差UMN= 90 V。
【考点】电荷性质、电势能和电势的关系;电场力做功与电势能变化的关系.
【专题】定量思想;推理法;带电粒子在电场中的运动专题;推理论证能力.
【答案】40,90。
【分析】根据电势差的定义式计算两点之间的电势差,然后根据U0M=0﹣φM计算M点的电势。
【解答】解:零电势点和M点的电势差为U0M,根据U0M=0﹣φM可得M点的电势为40V
M、N两点间的电势差UMN
故答案为:40,90。
【点评】掌握电势差的计算公式是解题的基础。
11.(2024春 东城区校级期末)如图甲是某电场中的一条电场线,a、b是这条线上的两点。若将一负点电荷从a点由静止释放,负电荷只受电场力作用,沿电场线从a运动到b。在这过程中,电荷的速度—时间图线如图乙所示。比较a、b两点电势的高低关系是φa < φb,场强的大小关系是Ea = Eb。(选填“>”“<”或“=”)
【考点】电势的定义、单位和物理意义及用定义式计算电势;电场线的定义及基本特征.
【专题】定性思想;推理法;电场力与电势的性质专题;推理论证能力.
【答案】<,=。
【分析】从速度—时间图线得到负电荷做匀加速运动,加速度不变,根据牛顿第二定律得到电场力的变化情况;电势的高低看电场线的指向,沿着电场线电势降低。
【解答】解:负电子从a运动到b,由速度—时间图线得到负电荷做加速运动,故电场力向右;
因为图线的斜率不变,故加速度不变,因此电场力不变,所以电场强度不变,即Ea=Eb;
负电荷受到的电场力与场强方向相反,故场强向左,沿场强方向,电势降低,故b点电势较大,即φa<φb。
故答案为:<,=。
【点评】本题关键通过速度—时间图象得到物体的速度变化情况和加速度变化情况,然后判断场强方向和电势大小。
四.解答题(共4小题)
12.(2024春 天心区校级期末)如图(a),同一竖直平面内A、B、M、N四点距O点的距离均为,O为水平连线AB的中点,M、N在AB连线的中垂线上。A、B两点分别固定有一点电荷,电荷量均为Q(Q>0)。以O为原点,竖直向下为正方向建立x轴。若取无穷远处为电势零点,则ON上的电势φ随位置x的变化关系如图(b)所示。一电荷量为Q(Q>0)的小球S1以一定初动能从M点竖直下落,一段时间后经过N点,其在ON段运动的加速度大小a随位置x的变化关系如图(c)所示。图中g为重力加速度大小,k为静电力常量。
(1)求M点的电场强度;
(2)求小球S1的重力;
(3)为保证S1能运动到N点,S1从M点下落时的初动能须满足什么条件?
【考点】带电粒子(计重力)在非匀强电场中的直线运动;点电荷与均匀带电球体(球壳)周围的电场;电场强度的叠加.
【专题】计算题;定量思想;图析法;动能定理的应用专题;带电粒子在电场中的运动专题;分析综合能力.
【答案】(1)M点的电场强度大小为,方向由O指向M;
(2)小球S1的重力为;
(3)为保证S1能运动到N点,S1从M点下落时的初动能须满足。
【分析】(1)根据点电荷的场强公式结合矢量的合成求解M点的电场强度大小,判断其方向;
(2)根据牛顿第二定律结合力的合成可解得小球S1的重力;
(3)为保证S1能运动到N点与S2相碰,S1运动到D点时的速度必须大于零,根据动能定理确定S1从M点下落时的初动能须满足的条件。
【解答】解:(1)由点电荷场强公式可得,单个点电荷在M点的场强大小为
两个点电荷在M点的电场强度方向垂直,则M点的电场强度为
EME
方向由O指向M。
(2)设O点下方处为C点,A与C的距离为RC,小球S1在C处所受的库仑力大小为FC,由库仑定律和力的合成有
式中
设小球S1的质量为m1,小球S1在C点的加速度大小为a,由牛顿第二定律有
FC+m1g=m1a
由图(c)可知,a=2g
联立并代入数据解得:
(3)设O点上方处为D点。根据图(c)和对称性可知,S1在D点所受的电场力大小等于小球的重力大小,方向竖直向上,S1在此处加速度为0;S1在D点上方做减速运动,在D点下方做加速运动,为保证S1能运动到N点,S1运动到D点时的速度必须大于零
设M点与D点电势差为UMD,由电势差与电势的关系有
UMD=φM﹣φD
设小球S1初动能为Ek,运动到D点的动能为EkD,由动能定理有
m1g(MO﹣DO)+QUMD=EkD﹣Ek
其中EkD>0
由对称性,D点与C点电势相等,M点与N点电势相等,依据图(b)所给数据,联立解得:
即为保证S1能运动到N点,S1从M点下落时的初动能须满足。
答:(1)M点的电场强度大小为,方向由O指向M;
(2)小球S1的重力为;
(3)为保证S1能运动到N点,S1从M点下落时的初动能须满足。
【点评】本题考查牛顿第二定律、动能定理,结合带电粒子在电场中运动的规律,解题关键掌握粒子的运动情况分析,有一定的难度。
13.(2024秋 天心区校级期末)如图,水平地面上放置一长度L=10m、质量M=1kg的长木板。一可视为质点、质量m=1kg、带电量q=+1×10﹣5C的小物块放在木板上,小物块到木板右端距离d1=7m。在距木板右端d2=9m的虚线右侧,存在宽度d3=11.5m的匀强电场,场强E1=2×106N/C,方向竖直向下。匀强电场E1右侧存在宽度,d4=6m的匀强电场,场强E2=1×106N/C,方向竖直向上。从t=0时刻起,水平恒力F=8N作用在长木板上,5s末撤去。已知物块与长木板间的动摩擦因数μ1=0.4,长木板与水平地面间的动摩擦因数μ2=0.2,物块带电量始终不变,重力加速度g取10m/s2,求:
(1)物块运动多长时间进入匀强电场E1;
(2)物块离开匀强电场E2时速度的大小;
(3)物块最终停下来时,离木板右端的距离。
【考点】从能量转化与守恒的角度解决电场中的问题;牛顿第二定律的简单应用.
【专题】定量思想;推理法;带电粒子在电场中的运动专题;分析综合能力.
【答案】(1)物块运动4s进入匀强电场E1;
(2)物块离开匀强电场E2时速度的大小6m/s;
(3)物块最终停下来时,离木板右端的距离5.5m。
【分析】(1)根据牛顿第二定律求出物块的加速度,结合题设条件确定物块和木板的运动状态,求得物块运动多长时间进入匀强电场;
(2)(3)由运动学规律进入电场的位移,进入电场后根据动力学规律物块的运动过程,再结合题设条件求物块离开匀强电场E2时速度的大小,物块最终停下来时,离木板右端的距离。
【解答】解:(1)在物块未进入电场时设其最大加速度大小为a0,则由牛顿第二定律有
μ1mg=ma0
解得
当给木板施加恒力时,假设物块和木板能够保持相对静止,一起做匀加速直线运动,设共同加速度的加速度大小为a,则对整体由牛顿第二定律有
F﹣μ2(m+M)g=(m+M)a
代入数据解得
a=2m/s2<a0
则假设成立,在未撤去力F的时间内物块的位移
可知
x0>d1+d2
则可知在力F撤去前的某一时间内物块已经进入电场,设从开始运动到物块进入电场的施加为t0,由位移与时间的关系可得
解得
t0=4s
(2)当物块进入电场E1后由于电场力竖直向下,增加了物块对木板的正压力同时也增加了木板对地面的正压力,因此可知木块仍相对于木板静止,在电场E1中,在力F未撤去时,设物块和木板共同运动的加速度大小为a1,由牛顿第二定律有
F﹣μ2[(m+M)g+Eq]=(m+M)a1
解得
a1=0
即在物块进入电场E1中的1s时间内物块和木板一起做匀速直线运动,设其位移为x1,进入电场E1时的速度大小为v1,则有
v1=at0=2×4m/s=8m/s
x1=v1t1=8×1m=8m
此时距进入电场E2的距离为
x2=d3﹣x1=11.5m﹣8m=3.5m
设在这段位移内物块和木板共同运动的加速度大小为a′1,由牛顿第二定律有
μ2[(m+M)g+Eq]=(m+M)a′1
解得
设物块和木板共同进入电场E2时的速度大小为v2,则由速度与位移的关系可得
解得
v2=6m/s
当进入匀强电场E2,电场力竖直向上,对物块在竖直方向有
mg=E2q
可知,物块在电场E2中做匀速直线运动,因此,物块离开匀强电场E2时速度的大小为6m/s。
(3)设物块出电场E2所用的时间为t2,在物块出电场E2的过程中木板在电场E2中做匀减速直线运动的加速度大小为a2,则有
d4=v2t2
μ2Mg=Ma2
解得
t2=1s,
设该过程中木板的位移为x3,可得
解得
x3=5m
则可得物块出电场E2时距离木板右端的距离为
d5=d1﹣(d4﹣x3)
解得
d5=6m
此时木板的速度
v3=v2﹣a2t2
解得
v3=4m/s
此后在两者达到共速前物块的加速度大小为,设木板的加速度大小为a3,对木板由牛顿第二定律有
μ1mg﹣μ2(m+M)g=Ma3
解得
a3=0
即物块出电场E2后做匀减速直线运动,而木板做匀速直线运动,设达到共速所用时间为t3,根据速度—时间关系可得
v3=v2﹣a0t3
解得
t3=0.5s
则在该时间内物块和木板的位移分别为x4、x5,则根据位移与时间的关系有
x5=v3t3=4×0.5m=2m
两者达到共速后将一起做减速运动,直至停止,则可知物块最终离木板右端的距离为
d6=d5﹣(x4﹣x5)
解得
d6=5.5m
答:(1)物块运动4s进入匀强电场E1;
(2)物块离开匀强电场E2时速度的大小6m/s;
(3)物块最终停下来时,离木板右端的距离5.5m。
【点评】本题难度较大,这是一道涉及电场的在水平面上的有拉力的板块模型,一定要分清两个物体的运动状态,用动力学规律可以解决相应的问题。
14.(2024秋 厦门期末)如图甲所示,一倾角为30°足够长的绝缘斜面固定在水平地面上,质量为m、电荷量为﹣q(q>0)的物块A压缩轻质绝缘微型弹簧a后锁定(A与弹簧不拴接)。空间中存在沿斜面向上、大小E(g为重力加速度)的匀强电场。质量为2m、电荷量为+q的物块B静止在斜面上端,B左侧固定有处于原长的轻质绝缘弹簧b,A、B与斜面的滑动摩擦力大小分别为mg、mg,最大静摩擦力等于滑动摩擦力。
t=0时解除锁定,弹簧的弹性势能Ep瞬间全部转化为A的动能,A运动距离L后于t1时刻到达P点,此时速度为v1、加速度为0,且未与弹簧b接触;t2时刻,A到达Q点,速度达到最大值2v1,弹簧b的弹力大小为mg,此过程中A的v﹣t图像如图乙所示。已知A、B的电荷量始终保持不变,两者间的库仑力等效为真空中点电荷间的静电力,静电力常量为k,弹簧始终在弹性限度内。求:
(1)弹射过程弹簧a对A冲量的大小;
(2)A从开始运动到P点的过程中,B对A库仑力所做的功;
(3)A到达P点时,A与B之间的距离;
(4)A从P点运动到Q点的过程中,A、B系统(含弹簧b)的电势能变化量与弹性势能变化量的总和。
【考点】从能量转化与守恒的角度解决电场中的问题;动能定理的简单应用;常见力做功与相应的能量转化;动量定理的内容和应用;电场力做功与电势能变化的关系.
【专题】定量思想;方程法;带电粒子在复合场中的运动专题;分析综合能力.
【答案】(1)弹射过程弹簧a对A冲量的大小为;
(2)A从开始运动到P点的过程中,B对A库仑力所做的功为mgLEp;
(3)A到达P点时,A与B之间的距离为;
(4)A从P点运动到Q点的过程中,A、B系统(含弹簧b)的电势能变化量与弹性势能变化量的总和为。
【分析】(1)物块A压缩轻质绝缘微型弹簧a,弹簧的弹性势能Ep瞬间全部转化为A的动能,根据动能定理和动量定理求解;
(2)从A从开始运动到P点的过程中,根据动能定理求解B对A库仑力所做的功;
(3)A到达P点时,A的加速度为零,根据平衡条件进行解答;
(4)物块A在P点时,对B分析,分析B的受力情况和运动情况;以A和B整体为研究对象,根据动量守恒定律求解B的速度大小;滑块A在Q点时,二者之间的距离为x′,对A根据平衡条件求解A的位移,由此得到B的位移大小,对系统,根据能量守恒定律、功能关系可得A、B系统(含弹簧b)的电势能变化量与弹性势能变化量的总和。
【解答】解:(1)物块A压缩轻质绝缘微型弹簧a,弹簧的弹性势能Ep瞬间全部转化为A的动能,则有:Ep
解得:v
取沿斜面向上为正方向,根据动量定理可得弹射过程弹簧a对A冲量的大小为:I=mv﹣0=m;
(2)从A从开始运动到P点的过程中,根据动能定理可得:WBA﹣mgLsin30°mgL﹣qEL
解得B对A库仑力所做的功:WBAmgLEp;
(3)A到达P点时,A的加速度为零,则有:mgsin30°﹣qEmg=0
解得A与B之间的距离:x;
(4)物块A在P点时,对B分析,设此次B的摩擦力大小为f,则有:f2mgsin30°﹣qE
解得:f
此时B的摩擦力达到最大,此后A向上运动过程中,B向下运动。
以A和B整体为研究对象,合外力为:F合=3mgsin30°mgmg=0
说明A从P到Q运动过程中,系统合外力为零,则动量守恒;当A到Q点时,设B的速度大小为vB,取沿斜面向上为正方向,根据动量守恒定律可得:
mv1=m 2v1+2mvB
解得:vBv1
滑块A在Q点时,二者之间的距离为x′,对A根据平衡条件有:mg﹣mgsin30°﹣qEmg=0
解得:x′
由于A和B的合外力大小相等,而B的质量为A的质量的2倍,则B的加速度始终为A的一半,则A的位移等于B的位移的2倍。
则从A从P到Q过程中,二者的位移之和位移为:xA+xB=x﹣x′
B的位移为:xB()
对系统,根据能量守恒定律可得:W电场力+W弹簧+2mgxBsin30°﹣mgxAsin30°mgxAmgxB
解得:W电场力+W弹簧
根据功能关系可得A、B系统(含弹簧b)的电势能变化量与弹性势能变化量的总和:ΔEP=﹣W电场力+W弹簧
则ΔEp。
答:(1)弹射过程弹簧a对A冲量的大小为;
(2)A从开始运动到P点的过程中,B对A库仑力所做的功为mgLEp;
(3)A到达P点时,A与B之间的距离为;
(4)A从P点运动到Q点的过程中,A、B系统(含弹簧b)的电势能变化量与弹性势能变化量的总和为。
【点评】本题主要是考查带电物块在电场中的运动,关键是弄清楚物块的受力情况和运动情况,结合动能定理、功能关系进行解答。
15.(2024春 宿州期末)如图所示,由电子枪发出的电子从静止开始经加速电场加速后,沿平行于板面的方向射入偏转电场,并从另一侧射出。已知电子质量为m,电荷量为e,加速电场电压为U0,偏转电场可视为匀强电场,偏转电极YY'之间电压为U,极板长度为L,两极板间距离为d。不计电子重力和电子间相互作用,求:
(1)电子离开加速电场时的速度大小v0;
(2)电子在偏转电场中的加速度大小a;
(3)电子从偏转电场射出时沿垂直板面方向的偏转距离y。
【考点】从能量转化与守恒的角度解决电场中的问题.
【专题】计算题;定量思想;推理法;带电粒子在电场中的运动专题.
【答案】见试题解答内容
【分析】(1)在加速电场中动能定理可求出电子离开电场的速度;
(2)在偏转电场中,由牛顿第二定律可求出加速度大小;
(3)在偏转电场中,电子做类平抛运动,根据平抛运动的规律求出竖直方向的位移y。
【解答】解:(1)在加速电场中,由动能定理可知:eU0
解得:v0
(2)电子在偏转电场中,竖直方向只受电场力作用,由牛顿第二定律可知:
F=ma
F=eE=e
解得:a
(3)电子在偏转电场中做类平抛运动,
水平方向:L=v0t
竖直方向:yat2
联立解得:y
答:(1)电子离开加速电场时的速度大小v0为;
(2)电子在偏转电场中的加速度大小a为;
(3)电子从偏转电场射出时沿垂直板面方向的偏转距离y为。
【点评】本题考查带电粒子在加速电场和偏转电场中的运动,在加速电场中动能定理求末速度;
在偏转电场中做类平抛运动,根据平抛运动的规律求出相关物理量。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第九章 静电场及其应用
- 1 电荷
- 2 库仑定律
- 3 电场 电场强度
- 4 静电的防止与利用
- 第十章 静电场中的能量
- 1 电势能和电势
- 2 电势差
- 3 电势差与电场强度的关系
- 4 电容器的电容
- 5 带电粒子在电场中的运动
- 第十一章 电路及其应用
- 1 电源和电流
- 2 导体的电阻
- 3 实验:导体电阻率的测量
- 4 串联电路和并联电路
- 5 实验:练习使用多用电表
- 第十二章 电能 能量守恒定律
- 1 电路中的能量转化
- 2 闭合电路的欧姆定律
- 3 实验:电池电动势和内阻的测量
- 4 能源与可持续发展
- 第十三章 电磁感应与电磁波初步
- 1 磁场 磁感线
- 2 磁感应强度 磁通量
- 3 电磁感应现象及应用
- 4 电磁波的发现及应用
- 5 能量量子化
