辽宁省鞍山市铁东区2025届九年级下学期中考三模数学试卷(含详解)
文档属性
| 名称 | 辽宁省鞍山市铁东区2025届九年级下学期中考三模数学试卷(含详解) | 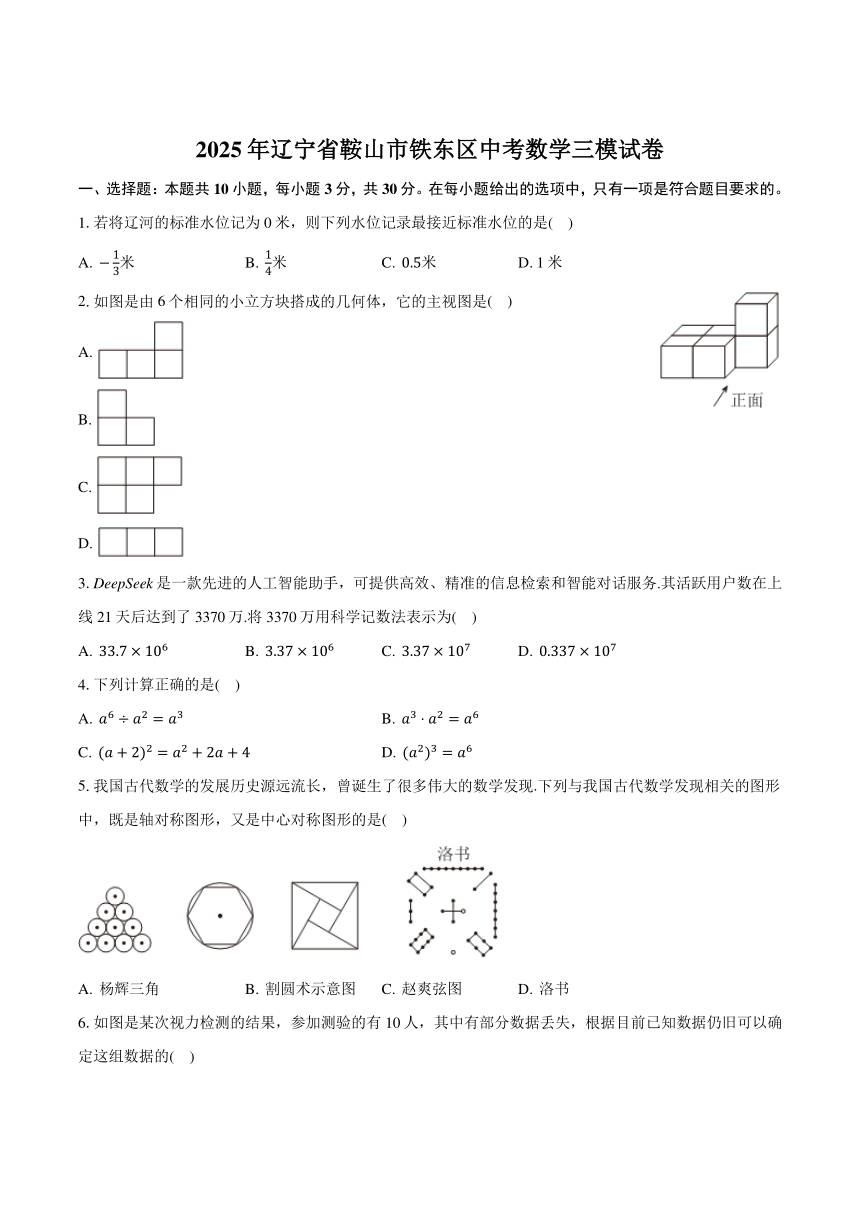 | |
| 格式 | docx | ||
| 文件大小 | 172.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 20:54:46 | ||
图片预览





文档简介
2025年辽宁省鞍山市铁东区中考数学三模试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若将辽河的标准水位记为0米,则下列水位记录最接近标准水位的是( )
A. 米 B. 米 C. 米 D. 1米
2.如图是由6个相同的小立方块搭成的几何体,它的主视图是( )
A.
B.
C.
D.
3.DeepSeek是一款先进的人工智能助手,可提供高效、精准的信息检索和智能对话服务.其活跃用户数在上线21天后达到了3370万.将3370万用科学记数法表示为( )
A. B. C. D.
4.下列计算正确的是( )
A. B.
C. D.
5.我国古代数学的发展历史源远流长,曾诞生了很多伟大的数学发现.下列与我国古代数学发现相关的图形中,既是轴对称图形,又是中心对称图形的是( )
A. 杨辉三角 B. 割圆术示意图 C. 赵爽弦图 D. 洛书
6.如图是某次视力检测的结果,参加测验的有10人,其中有部分数据丢失,根据目前已知数据仍旧可以确定这组数据的( )
视力
人数 1 2 4
A. 平均数,方差 B. 中位数,平均数 C. 中位数,众数 D. 方差,中位数
7.如图,已知,,,则等于( )
A.
B.
C.
D.
8.《九章算术》“盈不足”中有如下记载:今有共买琎ì,人出半,盈四;人出少半,不足三.问人数、进价各几何?译文:今有人合伙买琎石,每人出钱,会多4钱;每人出钱,又差3钱.问人数和琎石的价格各是多少?设人数为x,则可列方程为( )
A. B.
C. D.
9.如图是一架人字梯及其侧面示意图,已知,,,,则BF的长为( )
A. 27cm B. 50cm C. 72cm D. 80cm
10.已知点、、在反比例函数的图象上,则a、b、c的大小关系是( )
A. B. C. D.
二、填空题:本题共5小题,每小题3分,共15分。
11.不等式的解集是______.
12.如图,已知的边BC在x轴上,,且点,若将平移,使点B落在点A处,则点C的对应点的坐标为______.
13.“服务社会,提升自我.”宁波市某学校积极开展志愿者服务活动,来自九年级的3名同学两男一女成立了“交通秩序维护”小分队.若从该小分队任选两名同学进行交通秩序维护,则恰是一男一女的概率是______.
14.如图,点E是矩形ABCD的对角线AC的延长线上一点,若,,则______.
15.如图,在中,按以下步骤作图:①以点A为圆心,小于AC长为半径作弧,分别交AC,AB于点D,E;②分别以点D,E为圆心,大于长为半径作弧,两弧交于点F,作射线AF;③分别以点B,C为圆心,大于长为半径作弧,两弧交于M,N两点;④作直线MN交射线AF于点P,交CB于点G,交AB于点若,,则PG的长为______.
三、计算题:本大题共1小题,共9分。
16.端午节到了,某商场出售A,B两种粽子礼盒,其中B种礼盒单价是A种礼盒的倍,已知用2000元购买A种礼盒的数量,比用2400元购买B种礼盒的数量多5盒,求A,B两种粽子礼盒的单价分别是多少元?
四、解答题:本题共7小题,共66分。解答应写出文字说明,证明过程或演算步骤。
17.本小题9分
计算:
;
18.本小题9分
某学校为了解学生对“航空航天知识”的掌握情况,从七年级随机抽取部分同学进行测试,并对成绩百分制进行整理、描述和分析,下面给出部分信息:
学生成绩的统计图如图数据分为五组:,,,,
在这一组成绩的是80、80、80、81、81、82、83、84、84、85、85、87、88、89、89、
成绩不低于90分为优秀.
根据以上信息,回答下列问题:
本次调查采用的方式是______选填“全面调查”或“抽样调查”样本容量是______;
补全频数分布直方图;
若七年级有400名学生,请估计该校七年级学生达到优秀的人数.
19.本小题9分
如图1是某商场的入口,它是由立桂、斜杆、支撑杆组成的支架撑起的,如图2是它的示意图,点P、A、C在同一水平线上,经过测量,支架的立柱BC与地面PC垂直,米,支撑杆于点E,且,从点B观测点D的仰角为,又测得米.
求该支架的边BD的长;
求支架的边BD的顶端点D到地面PC的距离结果保留根号
20.本小题9分
每年的3月3日为全国爱耳日,今年的主题是“科技助残,共享美好生活”,某公司新研发了一批耳背式助听器计划在该月销售,根据市场调查,每个助听器盈利60元时,每天可售出50个;单价每降低2元,每天可多售出5个.公司决定在成本不变的情况下降价销售,但每个助听的利润不低于40元,设每个助听器降价x元,每天的销售利润为y元.
求y与x的函数关系式;每个助听器降价多少元时,每天的销售利润最大?最大利润为多少元;
全国爱耳日当天,公司共获得销售利润3750元,请问这天售出了多少个助听器.
21.本小题9分
如图,在中,四边形ACDB是圆内接四边形,AB是的直径,,过D作交AC延长线于点E,连接
求证:DE为的切线;
若,,求的半径长.
22.本小题9分
【问题背景】
如图1,点P是线段,AB,CD的中点,求证:;
【变式迁移】
如图2,在等腰中,BD是底边AC上的高线,点E为内一点,连接ED,延长ED到点F,使,连接AF,若,请判断AF、BE、BC三边数量关系并说明理由;
【拓展应用】
如图3,在等腰中,,,点D为AB中点,点E在线段BD上点E不与点B,点D重合,连接CE,过点A作,连接FD,若,,请直接写出FD的长.
23.本小题12分
定义:若点为常数且在函数F的图象上,则点A称为这个函数F的k倍值点.例如:点是函数的2倍值点,点是函数:的倍值点.
若点B是函数的2倍值点,求点B的坐标;
已知函数有且只有一个k倍值点C,求k的值;
函数图象与函数图象交于D,E两点,函数有D,F两个k倍值点,求的面积.
答案和解析
1.B
解:,
,
上列水位记录最接近标准水位的是米,
故选:
2.A
解:从几何体的正面看,底层是三个小正方形,上层的右端是一个小正方形.
故选:
3.C
解:3370万
故选:
4.D
解:,则A不符合题意,
,则B不符合题意,
,则C不符合题意,
,则D符合题意,
故选:
5.B
解:杨辉三角是轴对称图形,不是中心对称图形,不符合题意;
B.割圆术示意图既是轴对称图形,又是中心对称图形,符合题意;
C.赵爽弦图是中心对称图形,不是轴对称图形,不符合题意;
D.洛书既不是轴对称图形,也不是中心对称图形,不符合题意.
故选:
6.C
解:根据表格数据,可得视力为和的总人数为人,
视力为所占人数最多为4,因此众数为,
从小到大排列后中间两个数是、,因此中位数为,
则与被遮盖的数据无关的是中位数和众数,
数据不全无法求平均数,也不能求方差.
故选:
7.C
解:,
,
又,
故选:
8.D
解:根据“每人出钱,会多4钱;每人出钱,又差3钱”可得:,
故选:
9.C
解:已知,,,,
,
,
解得:
,
,
故选:
10.B
解:比例函数中,,此函数图象在二、四象限,
,
点、在第四象限,
函数图象在第四象限内为增函数,
,
,
在第二象限,
,
、b、c的大小关系是,
故选:
11.
解:,
去括号,得:,
移项,得:,
合并同类项,得:,
系数化为1,得:
故答案为:
12.
解:将平移,使点B落在点A处,点,,
坐标的变化规律为横坐标,纵坐标,
,
点C的对应点的坐标为是,即
故答案为:
13.
解:列表如下:
男 男 女
男 男,男 男,女
男 男,男 男,女
女 女,男 女,男
共有6种等可能的结果,其中恰是一男一女的结果有4种,
恰是一男一女的概率为
故答案为:
列表可得出所有等可能的结果数以及恰是一男一女的结果数,再利用概率公式可得出答案.
本题考查列表法与树状图法、概率公式,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
14.
解:四边形ABCD是矩形,
,
,
,
,
,
,
故答案为:
15.2
解:由作图可知GQ垂直平分线段BC,
,,
,
,
,,,
,
,,
平分,
,
,
故答案为:
16.解:设A种粽子礼盒的单价是x元,则B种粽子礼盒的单价是元,由题意得:
,
解得:,
经检验,是原方程的解,且符合题意,
答:A种粽子礼盒的单价是80元,则B种粽子礼盒的单价是120元.
设A种粽子礼盒的单价是x元,则B种粽子礼盒的单价是元,即可得出关于x的分式方程,解之经检验后即可得出结论;
17.;
解:原式
;
原式
18.抽样调查,50;
见解析;
104名.
本次调查采用的方式是抽样调查,样本容量是:;
故答案为:抽样调查,50;
成绩在这一组的共有16名,成绩在这一组的有名,
补全频数分布直方图如下:
名,
答:估计该校七年级学生达到优秀的人数有104名.
19.解:,
是直角三角形,
在中,,
,
,
即该支架的边BD的长为10米;
根据已知可得,在中,且,
,
即,
解得:,
在矩形GFCB中,,
米.
20.y与x的函数关系式为;每个助听器降价20元时,每天的销售利润最大,最大利润为4000元;
这天售出了75个助听器.
解:根据题意得:,
,
当时,y有最大值,最大值为4000,
答:y与x的函数关系式为;每个助听器降价20元时,每天的销售利润最大,最大利润为4000元;
根据题意得:,
解得:,,
每个助听的利润不低于40元,
,
此时,
这天售出了75个助听器.
21.见解析;
的半径长为
证明:连接OD,
四边形ACDB是圆内接四边形,
,
,
,
,
,
,
,
,
,
是的半径,
为的切线;
解:,
,
,
,
,
,
,
,
过E作于H,
,
,
,
,
过C作于G,
,
,,
设,
,
,
,
故的半径长为
22.证明:点P是线段AB,CD的中点,
,,
在与中,
,
≌,
,
;
解:,理由如下:
连接CE,如图:
是等腰三角形,BD是底边AC上的高线,
,
在与中,
,
≌,
,,
,
,
,
,
;
解:延长FD到T,使得,连接BT,延长CE交BT于点J,如图:
为AB的中点,
,
在与中,
,
≌,
,,
,
,
,
,
,,
,
,
≌,
,,
,
,
,
,
23.或;
或;
解:点B是函数的2倍值点,
,
,
解得,
或;
函数有且只有一个k倍值点,
只有一个根,
,
解得或;
图象与函数图象交于D,E两点,
有两个不相等的实数根,
整理得:,
函数有D,F两个k倍值点,
有两个不相等的实数根,
整理得:,
与的交点为D,
,解得,
,
,,
直线EF的解析式为,
过点D作轴交直线EF于点G,
,
的面积
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若将辽河的标准水位记为0米,则下列水位记录最接近标准水位的是( )
A. 米 B. 米 C. 米 D. 1米
2.如图是由6个相同的小立方块搭成的几何体,它的主视图是( )
A.
B.
C.
D.
3.DeepSeek是一款先进的人工智能助手,可提供高效、精准的信息检索和智能对话服务.其活跃用户数在上线21天后达到了3370万.将3370万用科学记数法表示为( )
A. B. C. D.
4.下列计算正确的是( )
A. B.
C. D.
5.我国古代数学的发展历史源远流长,曾诞生了很多伟大的数学发现.下列与我国古代数学发现相关的图形中,既是轴对称图形,又是中心对称图形的是( )
A. 杨辉三角 B. 割圆术示意图 C. 赵爽弦图 D. 洛书
6.如图是某次视力检测的结果,参加测验的有10人,其中有部分数据丢失,根据目前已知数据仍旧可以确定这组数据的( )
视力
人数 1 2 4
A. 平均数,方差 B. 中位数,平均数 C. 中位数,众数 D. 方差,中位数
7.如图,已知,,,则等于( )
A.
B.
C.
D.
8.《九章算术》“盈不足”中有如下记载:今有共买琎ì,人出半,盈四;人出少半,不足三.问人数、进价各几何?译文:今有人合伙买琎石,每人出钱,会多4钱;每人出钱,又差3钱.问人数和琎石的价格各是多少?设人数为x,则可列方程为( )
A. B.
C. D.
9.如图是一架人字梯及其侧面示意图,已知,,,,则BF的长为( )
A. 27cm B. 50cm C. 72cm D. 80cm
10.已知点、、在反比例函数的图象上,则a、b、c的大小关系是( )
A. B. C. D.
二、填空题:本题共5小题,每小题3分,共15分。
11.不等式的解集是______.
12.如图,已知的边BC在x轴上,,且点,若将平移,使点B落在点A处,则点C的对应点的坐标为______.
13.“服务社会,提升自我.”宁波市某学校积极开展志愿者服务活动,来自九年级的3名同学两男一女成立了“交通秩序维护”小分队.若从该小分队任选两名同学进行交通秩序维护,则恰是一男一女的概率是______.
14.如图,点E是矩形ABCD的对角线AC的延长线上一点,若,,则______.
15.如图,在中,按以下步骤作图:①以点A为圆心,小于AC长为半径作弧,分别交AC,AB于点D,E;②分别以点D,E为圆心,大于长为半径作弧,两弧交于点F,作射线AF;③分别以点B,C为圆心,大于长为半径作弧,两弧交于M,N两点;④作直线MN交射线AF于点P,交CB于点G,交AB于点若,,则PG的长为______.
三、计算题:本大题共1小题,共9分。
16.端午节到了,某商场出售A,B两种粽子礼盒,其中B种礼盒单价是A种礼盒的倍,已知用2000元购买A种礼盒的数量,比用2400元购买B种礼盒的数量多5盒,求A,B两种粽子礼盒的单价分别是多少元?
四、解答题:本题共7小题,共66分。解答应写出文字说明,证明过程或演算步骤。
17.本小题9分
计算:
;
18.本小题9分
某学校为了解学生对“航空航天知识”的掌握情况,从七年级随机抽取部分同学进行测试,并对成绩百分制进行整理、描述和分析,下面给出部分信息:
学生成绩的统计图如图数据分为五组:,,,,
在这一组成绩的是80、80、80、81、81、82、83、84、84、85、85、87、88、89、89、
成绩不低于90分为优秀.
根据以上信息,回答下列问题:
本次调查采用的方式是______选填“全面调查”或“抽样调查”样本容量是______;
补全频数分布直方图;
若七年级有400名学生,请估计该校七年级学生达到优秀的人数.
19.本小题9分
如图1是某商场的入口,它是由立桂、斜杆、支撑杆组成的支架撑起的,如图2是它的示意图,点P、A、C在同一水平线上,经过测量,支架的立柱BC与地面PC垂直,米,支撑杆于点E,且,从点B观测点D的仰角为,又测得米.
求该支架的边BD的长;
求支架的边BD的顶端点D到地面PC的距离结果保留根号
20.本小题9分
每年的3月3日为全国爱耳日,今年的主题是“科技助残,共享美好生活”,某公司新研发了一批耳背式助听器计划在该月销售,根据市场调查,每个助听器盈利60元时,每天可售出50个;单价每降低2元,每天可多售出5个.公司决定在成本不变的情况下降价销售,但每个助听的利润不低于40元,设每个助听器降价x元,每天的销售利润为y元.
求y与x的函数关系式;每个助听器降价多少元时,每天的销售利润最大?最大利润为多少元;
全国爱耳日当天,公司共获得销售利润3750元,请问这天售出了多少个助听器.
21.本小题9分
如图,在中,四边形ACDB是圆内接四边形,AB是的直径,,过D作交AC延长线于点E,连接
求证:DE为的切线;
若,,求的半径长.
22.本小题9分
【问题背景】
如图1,点P是线段,AB,CD的中点,求证:;
【变式迁移】
如图2,在等腰中,BD是底边AC上的高线,点E为内一点,连接ED,延长ED到点F,使,连接AF,若,请判断AF、BE、BC三边数量关系并说明理由;
【拓展应用】
如图3,在等腰中,,,点D为AB中点,点E在线段BD上点E不与点B,点D重合,连接CE,过点A作,连接FD,若,,请直接写出FD的长.
23.本小题12分
定义:若点为常数且在函数F的图象上,则点A称为这个函数F的k倍值点.例如:点是函数的2倍值点,点是函数:的倍值点.
若点B是函数的2倍值点,求点B的坐标;
已知函数有且只有一个k倍值点C,求k的值;
函数图象与函数图象交于D,E两点,函数有D,F两个k倍值点,求的面积.
答案和解析
1.B
解:,
,
上列水位记录最接近标准水位的是米,
故选:
2.A
解:从几何体的正面看,底层是三个小正方形,上层的右端是一个小正方形.
故选:
3.C
解:3370万
故选:
4.D
解:,则A不符合题意,
,则B不符合题意,
,则C不符合题意,
,则D符合题意,
故选:
5.B
解:杨辉三角是轴对称图形,不是中心对称图形,不符合题意;
B.割圆术示意图既是轴对称图形,又是中心对称图形,符合题意;
C.赵爽弦图是中心对称图形,不是轴对称图形,不符合题意;
D.洛书既不是轴对称图形,也不是中心对称图形,不符合题意.
故选:
6.C
解:根据表格数据,可得视力为和的总人数为人,
视力为所占人数最多为4,因此众数为,
从小到大排列后中间两个数是、,因此中位数为,
则与被遮盖的数据无关的是中位数和众数,
数据不全无法求平均数,也不能求方差.
故选:
7.C
解:,
,
又,
故选:
8.D
解:根据“每人出钱,会多4钱;每人出钱,又差3钱”可得:,
故选:
9.C
解:已知,,,,
,
,
解得:
,
,
故选:
10.B
解:比例函数中,,此函数图象在二、四象限,
,
点、在第四象限,
函数图象在第四象限内为增函数,
,
,
在第二象限,
,
、b、c的大小关系是,
故选:
11.
解:,
去括号,得:,
移项,得:,
合并同类项,得:,
系数化为1,得:
故答案为:
12.
解:将平移,使点B落在点A处,点,,
坐标的变化规律为横坐标,纵坐标,
,
点C的对应点的坐标为是,即
故答案为:
13.
解:列表如下:
男 男 女
男 男,男 男,女
男 男,男 男,女
女 女,男 女,男
共有6种等可能的结果,其中恰是一男一女的结果有4种,
恰是一男一女的概率为
故答案为:
列表可得出所有等可能的结果数以及恰是一男一女的结果数,再利用概率公式可得出答案.
本题考查列表法与树状图法、概率公式,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
14.
解:四边形ABCD是矩形,
,
,
,
,
,
,
故答案为:
15.2
解:由作图可知GQ垂直平分线段BC,
,,
,
,
,,,
,
,,
平分,
,
,
故答案为:
16.解:设A种粽子礼盒的单价是x元,则B种粽子礼盒的单价是元,由题意得:
,
解得:,
经检验,是原方程的解,且符合题意,
答:A种粽子礼盒的单价是80元,则B种粽子礼盒的单价是120元.
设A种粽子礼盒的单价是x元,则B种粽子礼盒的单价是元,即可得出关于x的分式方程,解之经检验后即可得出结论;
17.;
解:原式
;
原式
18.抽样调查,50;
见解析;
104名.
本次调查采用的方式是抽样调查,样本容量是:;
故答案为:抽样调查,50;
成绩在这一组的共有16名,成绩在这一组的有名,
补全频数分布直方图如下:
名,
答:估计该校七年级学生达到优秀的人数有104名.
19.解:,
是直角三角形,
在中,,
,
,
即该支架的边BD的长为10米;
根据已知可得,在中,且,
,
即,
解得:,
在矩形GFCB中,,
米.
20.y与x的函数关系式为;每个助听器降价20元时,每天的销售利润最大,最大利润为4000元;
这天售出了75个助听器.
解:根据题意得:,
,
当时,y有最大值,最大值为4000,
答:y与x的函数关系式为;每个助听器降价20元时,每天的销售利润最大,最大利润为4000元;
根据题意得:,
解得:,,
每个助听的利润不低于40元,
,
此时,
这天售出了75个助听器.
21.见解析;
的半径长为
证明:连接OD,
四边形ACDB是圆内接四边形,
,
,
,
,
,
,
,
,
,
是的半径,
为的切线;
解:,
,
,
,
,
,
,
,
过E作于H,
,
,
,
,
过C作于G,
,
,,
设,
,
,
,
故的半径长为
22.证明:点P是线段AB,CD的中点,
,,
在与中,
,
≌,
,
;
解:,理由如下:
连接CE,如图:
是等腰三角形,BD是底边AC上的高线,
,
在与中,
,
≌,
,,
,
,
,
,
;
解:延长FD到T,使得,连接BT,延长CE交BT于点J,如图:
为AB的中点,
,
在与中,
,
≌,
,,
,
,
,
,
,,
,
,
≌,
,,
,
,
,
,
23.或;
或;
解:点B是函数的2倍值点,
,
,
解得,
或;
函数有且只有一个k倍值点,
只有一个根,
,
解得或;
图象与函数图象交于D,E两点,
有两个不相等的实数根,
整理得:,
函数有D,F两个k倍值点,
有两个不相等的实数根,
整理得:,
与的交点为D,
,解得,
,
,,
直线EF的解析式为,
过点D作轴交直线EF于点G,
,
的面积
同课章节目录
