1.1 认识三角形 第2课时 三角形的分类及直角三角形的性质 导学案(含答案) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 1.1 认识三角形 第2课时 三角形的分类及直角三角形的性质 导学案(含答案) 2025-2026学年数学鲁教版(五四制)七年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 477.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-18 00:00:00 | ||
图片预览

文档简介
1.1认识三角形
第2课时 三角形的分类及直角三角形的性质
【学习目标】
1.理解锐角三角形 、直角三角形 、钝角三角形的概念,并会按角将三角形分成三类;
2.经历画图、实验、猜想、验证交流等活动过程,使学生学会实验探究问题的方法.
3.掌握“直角三角形的两个锐角互余”的性质,并能解决实际问题.
【新知探究】
[任务一:三角形的分类]
猜一猜:
(1)小明所拿三角形被遮住的这个内角是什么角 小颖的呢 试着说明理由.
(2)小亮所拿的三角形被遮住的两个内角可能是什么角 将所得结果与(1)中的结果进行比较.
总结:按三角形内角的大小把三角形分为三类
锐角三角形 三个内角都是锐角 直角三角形 有一个内角是直角 钝角三角形 有一个内角是钝角
【即时测评】
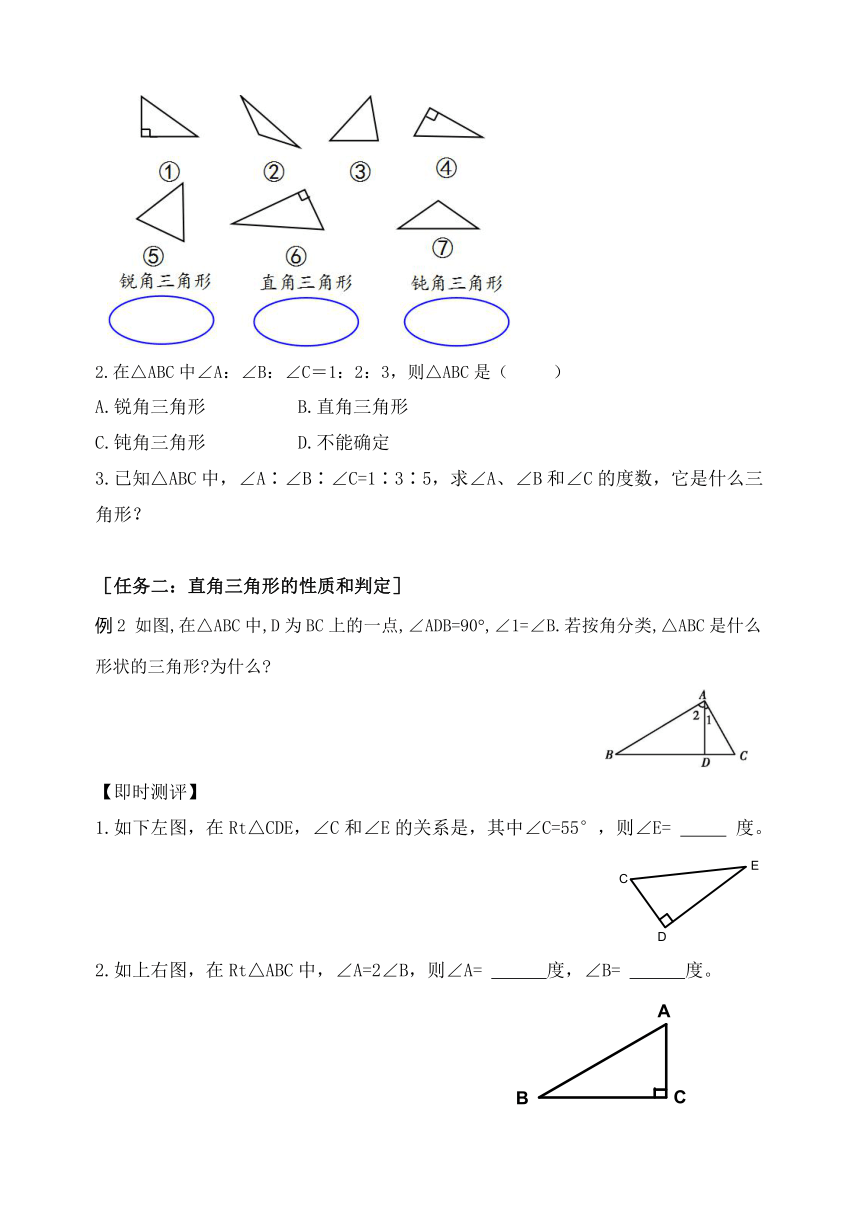
1.将下面的这些三角形按角进行分类。
2.在△ABC中∠A:∠B:∠C=1:2:3,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
3.已知△ABC中,∠A∶∠B∶∠C=1∶3∶5,求∠A、∠B和∠C的度数,它是什么三角形?
[任务二:直角三角形的性质和判定]
例2 如图,在△ABC中,D为BC上的一点,∠ADB=90°,∠1=∠B.若按角分类,△ABC是什么形状的三角形 为什么
【即时测评】
1.如下左图,在Rt△CDE,∠C和∠E的关系是,其中∠C=55°,则∠E= 度。
2.如上右图,在Rt△ABC中,∠A=2∠B,则∠A= 度,∠B= 度。
3.一个三角形两个内角的度数分别如下,这个三角形是什么三角形?
(1)30°和60°;(2)40°和70°;(3)50°和20°。
由上面我们可以得到:如果一个三角形有两个角互余,那么这个三角形是______三角形。
4.如图,在△ABC中,∠C=90°,CD⊥AB,垂足是D,
(1)图中有_____个直角三角形;
(2)在图中和∠B相等的角是_____,在图中和∠A相等的角是_____。
【课堂达标】
1.下列说法错误的是( )
A.一个三角形最多有三个锐角;
B. 一个三角形最少有两个锐角;
C.一个三角形最多有一个钝角或一个直角;
D.一个三角形可以有两个钝角或两个直角.
2.图中的三角形被木板遮住了一部分,那么这个三角形是( )
A.锐角三角形 B.直角角三角形
C.钝角三角形 D.以上都有可能
3.在一个三角形中,三个角的比值为1:2:3,则此三角形的形状是 .
4.如图,在△ABC中,∠C=90°,EF∥AB,∠1=50°,则∠B=_________
5.在△ABC中,已知∠A,∠B,∠C有如下的关系,请判断△ABC的形状.
(1)∠A:∠B:∠C =2:3:4 (2)∠B=2∠A,∠C =3∠A
答 案
[任务一:三角形的分类]
(1)小明所拿三角形被遮住的这个内角可能是锐角;小颖所拿三角形被遮住的这个内角可能是锐角;
(2)小亮所拿三角形被遮住的这个内角可能是直角,也可能是钝角.
【即时训练】
1.③⑤ ①④⑥ ②⑦
2.B
3.解:∵△ABC中∠A:∠B:∠C=1:3:5,
∴设∠A=x,则∠B=3x,∠C=5x,
∴∠A+∠B+∠C=180°,即x+3x+5x=180°,解得x=20°,
∴∠A=20°,∠B=60°,∠C=100°,
∴△ABC是钝角三角形.
[任务二:直角三角形的性质和判定]
例1 解:△ABC为直角三角形,理由如下:
∵∠ADB=90°,
∴△ADB为直角三角形,
∴∠B+∠2=90°,
又∵∠1=∠B,
∴∠1+∠2=90°,
即∠BAC=90°,
∴△ABC为直角三角形.
【即时训练】
1.35
2.60 30
3.直角
4.3 ∠2 ∠1
【当堂达标】
1.D 2.B 3.直角三角形 4.40° 5.(1)锐角三角形(2)直角三角形(3)钝角三角形
第2课时 三角形的分类及直角三角形的性质
【学习目标】
1.理解锐角三角形 、直角三角形 、钝角三角形的概念,并会按角将三角形分成三类;
2.经历画图、实验、猜想、验证交流等活动过程,使学生学会实验探究问题的方法.
3.掌握“直角三角形的两个锐角互余”的性质,并能解决实际问题.
【新知探究】
[任务一:三角形的分类]
猜一猜:
(1)小明所拿三角形被遮住的这个内角是什么角 小颖的呢 试着说明理由.
(2)小亮所拿的三角形被遮住的两个内角可能是什么角 将所得结果与(1)中的结果进行比较.
总结:按三角形内角的大小把三角形分为三类
锐角三角形 三个内角都是锐角 直角三角形 有一个内角是直角 钝角三角形 有一个内角是钝角
【即时测评】
1.将下面的这些三角形按角进行分类。
2.在△ABC中∠A:∠B:∠C=1:2:3,则△ABC是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.不能确定
3.已知△ABC中,∠A∶∠B∶∠C=1∶3∶5,求∠A、∠B和∠C的度数,它是什么三角形?
[任务二:直角三角形的性质和判定]
例2 如图,在△ABC中,D为BC上的一点,∠ADB=90°,∠1=∠B.若按角分类,△ABC是什么形状的三角形 为什么
【即时测评】
1.如下左图,在Rt△CDE,∠C和∠E的关系是,其中∠C=55°,则∠E= 度。
2.如上右图,在Rt△ABC中,∠A=2∠B,则∠A= 度,∠B= 度。
3.一个三角形两个内角的度数分别如下,这个三角形是什么三角形?
(1)30°和60°;(2)40°和70°;(3)50°和20°。
由上面我们可以得到:如果一个三角形有两个角互余,那么这个三角形是______三角形。
4.如图,在△ABC中,∠C=90°,CD⊥AB,垂足是D,
(1)图中有_____个直角三角形;
(2)在图中和∠B相等的角是_____,在图中和∠A相等的角是_____。
【课堂达标】
1.下列说法错误的是( )
A.一个三角形最多有三个锐角;
B. 一个三角形最少有两个锐角;
C.一个三角形最多有一个钝角或一个直角;
D.一个三角形可以有两个钝角或两个直角.
2.图中的三角形被木板遮住了一部分,那么这个三角形是( )
A.锐角三角形 B.直角角三角形
C.钝角三角形 D.以上都有可能
3.在一个三角形中,三个角的比值为1:2:3,则此三角形的形状是 .
4.如图,在△ABC中,∠C=90°,EF∥AB,∠1=50°,则∠B=_________
5.在△ABC中,已知∠A,∠B,∠C有如下的关系,请判断△ABC的形状.
(1)∠A:∠B:∠C =2:3:4 (2)∠B=2∠A,∠C =3∠A
答 案
[任务一:三角形的分类]
(1)小明所拿三角形被遮住的这个内角可能是锐角;小颖所拿三角形被遮住的这个内角可能是锐角;
(2)小亮所拿三角形被遮住的这个内角可能是直角,也可能是钝角.
【即时训练】
1.③⑤ ①④⑥ ②⑦
2.B
3.解:∵△ABC中∠A:∠B:∠C=1:3:5,
∴设∠A=x,则∠B=3x,∠C=5x,
∴∠A+∠B+∠C=180°,即x+3x+5x=180°,解得x=20°,
∴∠A=20°,∠B=60°,∠C=100°,
∴△ABC是钝角三角形.
[任务二:直角三角形的性质和判定]
例1 解:△ABC为直角三角形,理由如下:
∵∠ADB=90°,
∴△ADB为直角三角形,
∴∠B+∠2=90°,
又∵∠1=∠B,
∴∠1+∠2=90°,
即∠BAC=90°,
∴△ABC为直角三角形.
【即时训练】
1.35
2.60 30
3.直角
4.3 ∠2 ∠1
【当堂达标】
1.D 2.B 3.直角三角形 4.40° 5.(1)锐角三角形(2)直角三角形(3)钝角三角形
