6.3 一次函数的图象 第1课时 正比例函数的图象与性质 导学案(含答案) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 6.3 一次函数的图象 第1课时 正比例函数的图象与性质 导学案(含答案) 2025-2026学年数学鲁教版(五四制)七年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 290.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-19 00:00:00 | ||
图片预览


文档简介
3 一次函数的图象
第1课时 正比例函数的图象与性质
【学习目标】
1.理解函数图象的概念,会画正比例函数的图象.
2.掌握正比例函数的图象与性质,并能灵活运用解答有关问题.
3.在归纳正比例函数图象与性质的过程中感受几何直观,发展数形结合的能力和意识.
【新知探究】
[任务一 探究函数图象及正比例函数图象的画法]
活动1:函数图象的概念:
把一个函数的自变量x与对应的因变量y的值分别作为点的_______和______,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的_______.
活动2:探究正比例函数图象的画法
例1 请作出正比例函数y=2x的图象.
解:列表:
x … -2 -1 0 1 2 …
y=2x … …
描点:以上表中5组对应值作为点的坐标,依次为
___,___,____,____,____在直角坐标系内描出相应的点.
连线:把这些点依次连接起来,得到y=2x的图象.它是一条 _________
总结:由例1我们发现:作一个函数的图象需要三个步骤:_______________
活动3: 作出正比例函数y=3x的图象.
x … …
y=-3x … …
问题1:请同学们以小组为单位,讨论下面的问题,把得出的结论写出来.
(1)满足关系式y=3x的x,y所对应的点(x,y)都在正比例函数y=3x的图象上吗? ____________________
(2)正比例函数y=3x的图象上的点(x,y)都满足关系式y=3x吗?__________
问题2:思考正比例函数y=2x与y=3x的图象有什么共同特点?总结正比例函数y=kx的图象有什么特点?
问题3:既然我们得出正比例函数y=kx的图象是一条直线.那么在画正比例函数图象时有
没有什么简单的方法呢?
[即时测评]
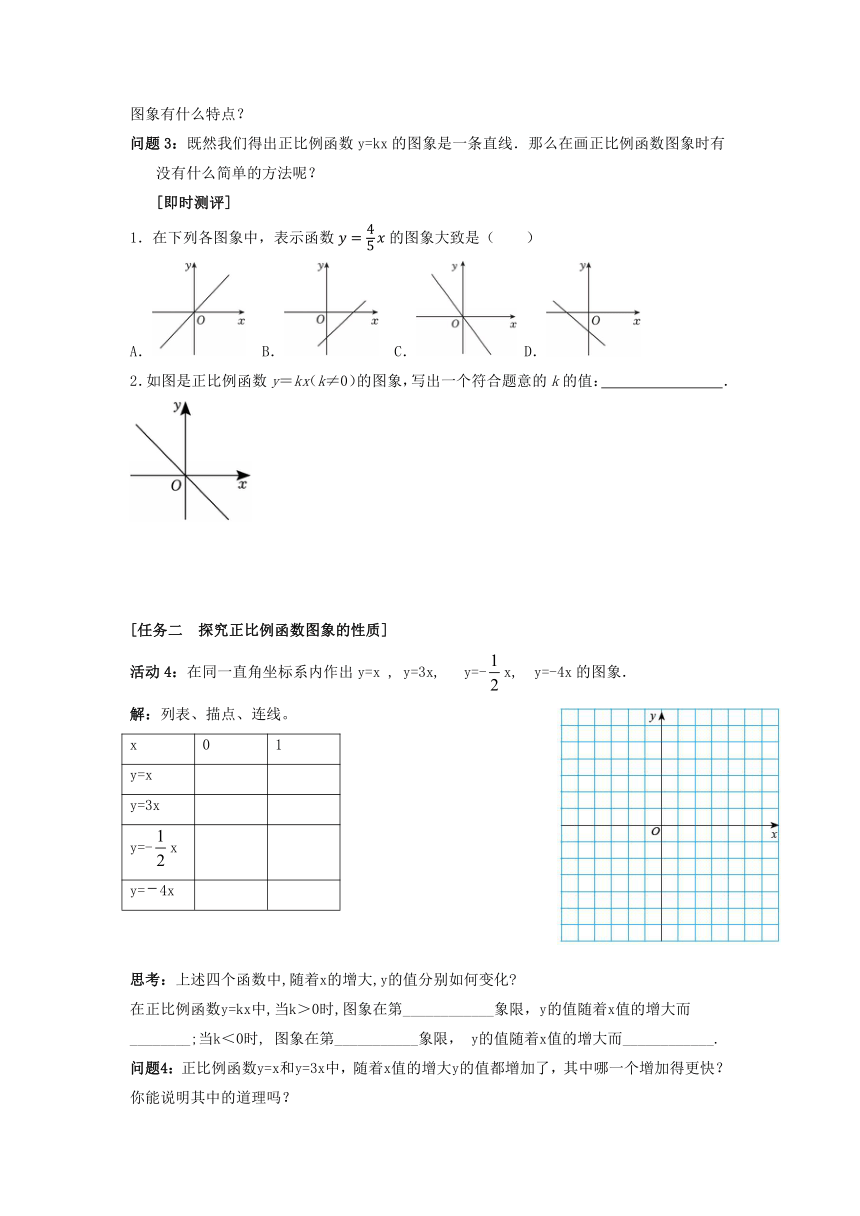
1.在下列各图象中,表示函数的图象大致是( )
A. B. C. D.
2.如图是正比例函数y=kx(k≠0)的图象,写出一个符合题意的k的值: .
[任务二 探究正比例函数图象的性质]
活动4:在同一直角坐标系内作出y=x , y=3x, y=-x, y=-4x的图象.
解:列表、描点、连线。
x 0 1
y=x
y=3x
y=-x
y=4x
思考:上述四个函数中,随着x的增大,y的值分别如何变化
在正比例函数y=kx中,当k>0时,图象在第____________象限,y的值随着x值的增大而________;当k<0时, 图象在第___________象限, y的值随着x值的增大而____________.
问题4:正比例函数y=x和y=3x中,随着x值的增大y的值都增加了,其中哪一个增加得更快?你能说明其中的道理吗?
(2)正比例函数y=-x和y=-4x中,随着x值的增大y的值都减小了,其中哪一个减小得更快?你是如何判断的?
归纳:
①|k|越 ,直线越 ,y的值增大(减小)的越 .
②|k|越 ,直线越 ,y的值增大(减小)的越 .
[即时测评]
1.下列哪些点在正比例函数y=-2x的图象上
A(1,2) B(-1,2) C (0.2,-0.4) D (-2,1)
2.函数y=-x的图象是一条过原点及(2,___)的直线,这条直线经过第_____象限,当x增大时,y随之________
3.画出下列正比例函数的图象
①y=x ②y= - x
[当堂达标]
1.正比例函数y=﹣2x的大致图象是( )
A. B. C. D.
2.若一个正比例函数的图象经过点(2,﹣3),则这个图象一定也经过点( )
A.(﹣3,2) B.(,﹣1) C.(,﹣1) D.(﹣,1)
3.如图,三个正比例函数的图象分别对应表达式:①y=ax,②y=bx,③y=cx,将a,b,c从小到大排列并用“<”连接为 .
4.已知正比例函数y=kx(k≠0)的图象经过点(﹣6,2),那么函数值y随自变量x的值的增大而 .(填“增大”或“减小”)
5.已知正比例函数y=kx(k≠0)图象上一个点A到x轴的距离为4,这个点A的横坐标为﹣2,请回答下列问题:
(1)求这个正比例函数;
(2)这个正比例函数经过哪几个象限?
(3)这个正比例函数的函数值y是随着x增大而增大?还是随着x增大而减小?
答案:
[任务一 探究函数图象及正比例函数图象的画法]
活动1:横坐标 纵坐标 图象
活动2:
例1 描点:﹣4 ﹣2 0 2 4
连线:直线
总结:列表、描点、连线
活动3:
解:列表:
x … -2 -1 0 1 2 …
y=-3x … 6 3 0 -3 -6 …
描点、连线
问题1:在
问题2:总结:正比例函数y=2x与y=3x的图象的共同特点:
(1)函数图象都经过原点 (0,0);
(2)函数图象都是一条直线.
正比例函数y=kx的图象是一条经过原点 (0,0)直线
问题3:因为“两点确定一条直线”,所以画正比例函数y=kx的图象时可以只描出两个点就可以了.因为正比例函数的图象是一条过原点(0,0)的直线,所以只需再确定一个点就可以了,通常过(0,0),(1,k)作直线.
[即时测评]
1.A
2.﹣1(答案不唯一)
[任务二 探究正比例函数图象的性质]
活动4:
解:列表、描点、连线。
x 0 1 2
y=x 0 1
y=3x 0 3
y=-x 0 -1
y=4x 0 -4
思考:一、三 增大;二、四 减小
问题4:(1)观察函数图象,可以看到对于任意一个 x 值, y = 3x 的函数值都是 y = x 的三倍,并且随着 x 的增加,y = 3x 的函数值增长速度更快.
(2)观察函数图象,可以看到对于任意一个 x 值, y = -4x 的函数值的绝对值都是 y = ﹣x 函数绝对值的八倍,并且随着 x 的增加,y = -4x 的函数值减小速度更快.
归纳:(1)大 陡 快 ;(2)小 坡 慢
[即时测评]
1.B
2.﹣3 二、四 减小
3.如图;
[当堂达标]
1.C
3.C.
3.a<c<b.
4.减小.
5.解:(1)∵正比例函数图象上一个点A到x轴的距离为4,这个点A的横坐标为﹣2,
∴A(﹣2,4),(﹣2,﹣4),
因为正比例y=kx经过点A,
所以4=﹣2k或﹣4=﹣2k,
解得k=﹣2或k=2,
故正比例函数解析式为;y=±2x;
(2)当y=2x时,图象经过第一、三象限;
当y=﹣2x时,图象经过第二、四象限;
(3)当y=2x时,函数值y是随着x增大而增大;
当y=﹣2x时,函数值y是随着x增大而减小.
第1课时 正比例函数的图象与性质
【学习目标】
1.理解函数图象的概念,会画正比例函数的图象.
2.掌握正比例函数的图象与性质,并能灵活运用解答有关问题.
3.在归纳正比例函数图象与性质的过程中感受几何直观,发展数形结合的能力和意识.
【新知探究】
[任务一 探究函数图象及正比例函数图象的画法]
活动1:函数图象的概念:
把一个函数的自变量x与对应的因变量y的值分别作为点的_______和______,在直角坐标系内描出它的对应点,所有这些点组成的图形叫做该函数的_______.
活动2:探究正比例函数图象的画法
例1 请作出正比例函数y=2x的图象.
解:列表:
x … -2 -1 0 1 2 …
y=2x … …
描点:以上表中5组对应值作为点的坐标,依次为
___,___,____,____,____在直角坐标系内描出相应的点.
连线:把这些点依次连接起来,得到y=2x的图象.它是一条 _________
总结:由例1我们发现:作一个函数的图象需要三个步骤:_______________
活动3: 作出正比例函数y=3x的图象.
x … …
y=-3x … …
问题1:请同学们以小组为单位,讨论下面的问题,把得出的结论写出来.
(1)满足关系式y=3x的x,y所对应的点(x,y)都在正比例函数y=3x的图象上吗? ____________________
(2)正比例函数y=3x的图象上的点(x,y)都满足关系式y=3x吗?__________
问题2:思考正比例函数y=2x与y=3x的图象有什么共同特点?总结正比例函数y=kx的图象有什么特点?
问题3:既然我们得出正比例函数y=kx的图象是一条直线.那么在画正比例函数图象时有
没有什么简单的方法呢?
[即时测评]
1.在下列各图象中,表示函数的图象大致是( )
A. B. C. D.
2.如图是正比例函数y=kx(k≠0)的图象,写出一个符合题意的k的值: .
[任务二 探究正比例函数图象的性质]
活动4:在同一直角坐标系内作出y=x , y=3x, y=-x, y=-4x的图象.
解:列表、描点、连线。
x 0 1
y=x
y=3x
y=-x
y=4x
思考:上述四个函数中,随着x的增大,y的值分别如何变化
在正比例函数y=kx中,当k>0时,图象在第____________象限,y的值随着x值的增大而________;当k<0时, 图象在第___________象限, y的值随着x值的增大而____________.
问题4:正比例函数y=x和y=3x中,随着x值的增大y的值都增加了,其中哪一个增加得更快?你能说明其中的道理吗?
(2)正比例函数y=-x和y=-4x中,随着x值的增大y的值都减小了,其中哪一个减小得更快?你是如何判断的?
归纳:
①|k|越 ,直线越 ,y的值增大(减小)的越 .
②|k|越 ,直线越 ,y的值增大(减小)的越 .
[即时测评]
1.下列哪些点在正比例函数y=-2x的图象上
A(1,2) B(-1,2) C (0.2,-0.4) D (-2,1)
2.函数y=-x的图象是一条过原点及(2,___)的直线,这条直线经过第_____象限,当x增大时,y随之________
3.画出下列正比例函数的图象
①y=x ②y= - x
[当堂达标]
1.正比例函数y=﹣2x的大致图象是( )
A. B. C. D.
2.若一个正比例函数的图象经过点(2,﹣3),则这个图象一定也经过点( )
A.(﹣3,2) B.(,﹣1) C.(,﹣1) D.(﹣,1)
3.如图,三个正比例函数的图象分别对应表达式:①y=ax,②y=bx,③y=cx,将a,b,c从小到大排列并用“<”连接为 .
4.已知正比例函数y=kx(k≠0)的图象经过点(﹣6,2),那么函数值y随自变量x的值的增大而 .(填“增大”或“减小”)
5.已知正比例函数y=kx(k≠0)图象上一个点A到x轴的距离为4,这个点A的横坐标为﹣2,请回答下列问题:
(1)求这个正比例函数;
(2)这个正比例函数经过哪几个象限?
(3)这个正比例函数的函数值y是随着x增大而增大?还是随着x增大而减小?
答案:
[任务一 探究函数图象及正比例函数图象的画法]
活动1:横坐标 纵坐标 图象
活动2:
例1 描点:﹣4 ﹣2 0 2 4
连线:直线
总结:列表、描点、连线
活动3:
解:列表:
x … -2 -1 0 1 2 …
y=-3x … 6 3 0 -3 -6 …
描点、连线
问题1:在
问题2:总结:正比例函数y=2x与y=3x的图象的共同特点:
(1)函数图象都经过原点 (0,0);
(2)函数图象都是一条直线.
正比例函数y=kx的图象是一条经过原点 (0,0)直线
问题3:因为“两点确定一条直线”,所以画正比例函数y=kx的图象时可以只描出两个点就可以了.因为正比例函数的图象是一条过原点(0,0)的直线,所以只需再确定一个点就可以了,通常过(0,0),(1,k)作直线.
[即时测评]
1.A
2.﹣1(答案不唯一)
[任务二 探究正比例函数图象的性质]
活动4:
解:列表、描点、连线。
x 0 1 2
y=x 0 1
y=3x 0 3
y=-x 0 -1
y=4x 0 -4
思考:一、三 增大;二、四 减小
问题4:(1)观察函数图象,可以看到对于任意一个 x 值, y = 3x 的函数值都是 y = x 的三倍,并且随着 x 的增加,y = 3x 的函数值增长速度更快.
(2)观察函数图象,可以看到对于任意一个 x 值, y = -4x 的函数值的绝对值都是 y = ﹣x 函数绝对值的八倍,并且随着 x 的增加,y = -4x 的函数值减小速度更快.
归纳:(1)大 陡 快 ;(2)小 坡 慢
[即时测评]
1.B
2.﹣3 二、四 减小
3.如图;
[当堂达标]
1.C
3.C.
3.a<c<b.
4.减小.
5.解:(1)∵正比例函数图象上一个点A到x轴的距离为4,这个点A的横坐标为﹣2,
∴A(﹣2,4),(﹣2,﹣4),
因为正比例y=kx经过点A,
所以4=﹣2k或﹣4=﹣2k,
解得k=﹣2或k=2,
故正比例函数解析式为;y=±2x;
(2)当y=2x时,图象经过第一、三象限;
当y=﹣2x时,图象经过第二、四象限;
(3)当y=2x时,函数值y是随着x增大而增大;
当y=﹣2x时,函数值y是随着x增大而减小.
