2.2 简单的轴对称图形 第3课时 等腰三角形的性质 导学案(含答案) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 2.2 简单的轴对称图形 第3课时 等腰三角形的性质 导学案(含答案) 2025-2026学年数学鲁教版(五四制)七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 250.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-19 13:34:25 | ||
图片预览


文档简介
2 简单的轴对称图形
第3课时 等腰三角形的性质
[学习目标]
1.探索并了解等腰三角形的性质;
2.知道等边三角形是特殊的等腰三角形,并掌握其性质.
3.在探索轴对称性质的过程中,能够进行有条理地思考并进行简单地推理.
[复习回顾]
观察下列各种图形,判断是不是轴对称图形,能找出对称轴吗?
[新知探究]
[任务一 探究等腰三角形的性质]
活动1:回顾等腰三角形中,有这样几个重要的概念:
(1)相等的两条边都叫 ;另一边叫 ;
(2)两腰的夹角∠A叫 ;
(3)腰与底边夹角∠B,∠C叫 .
活动2:同学们各自画一个等腰三角形,并动手将各自手中的三角形标上A,B,C.
将等腰三角形ABC纸板沿直线对折,我们将对折的痕迹标上AD.
问题1:结合我们之前学习的轴对称图形的意义,等腰三角形是轴对称图形吗 如果是,你能发现哪些相等的线段和相等的角?
问题2:等腰三角形的对称轴是一条怎样的直线?你是如何描述的?
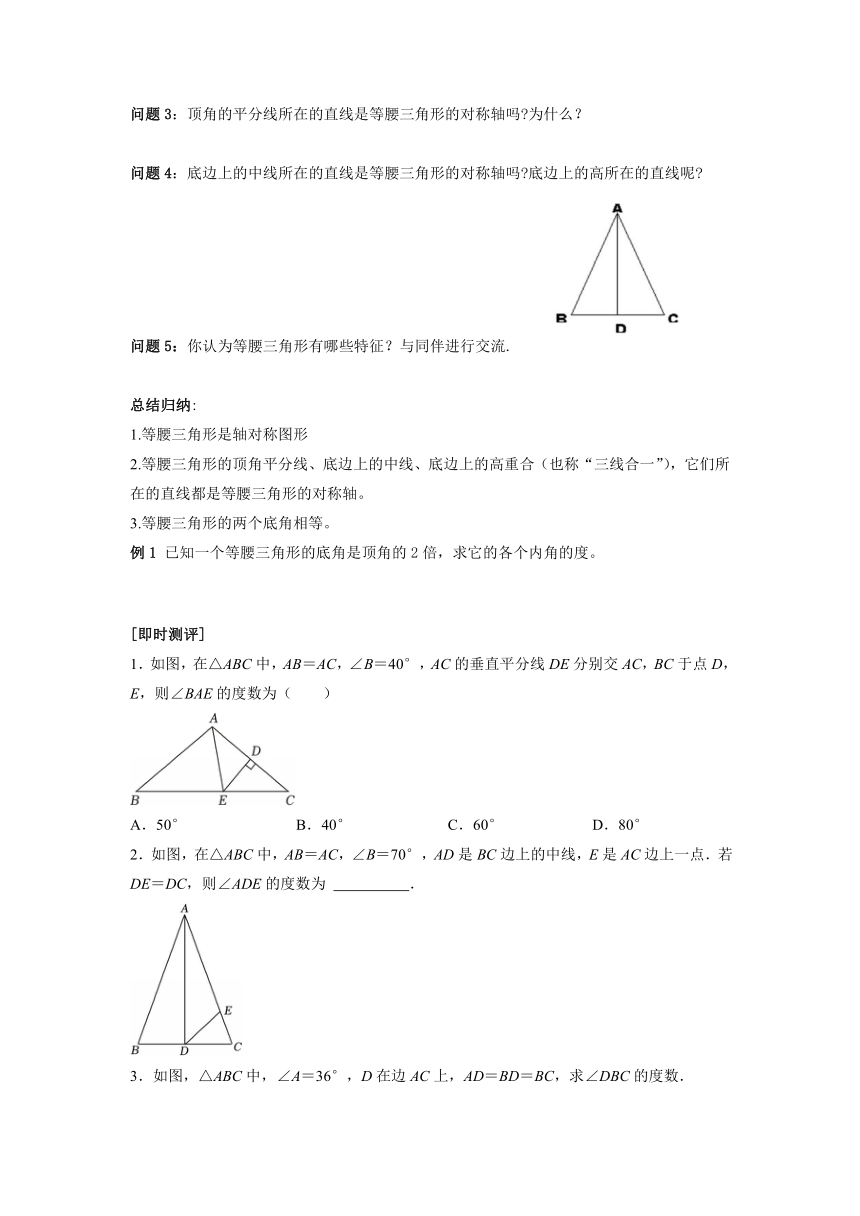
问题3:顶角的平分线所在的直线是等腰三角形的对称轴吗 为什么?
问题4:底边上的中线所在的直线是等腰三角形的对称轴吗 底边上的高所在的直线呢
问题5:你认为等腰三角形有哪些特征?与同伴进行交流.
总结归纳:
1.等腰三角形是轴对称图形
2.等腰三角形的顶角平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴。
3.等腰三角形的两个底角相等。
例1 已知一个等腰三角形的底角是顶角的2倍,求它的各个内角的度。
[即时测评]
1.如图,在△ABC中,AB=AC,∠B=40°,AC的垂直平分线DE分别交AC,BC于点D,E,则∠BAE的度数为( )
A.50° B.40° C.60° D.80°
2.如图,在△ABC中,AB=AC,∠B=70°,AD是BC边上的中线,E是AC边上一点.若DE=DC,则∠ADE的度数为 .
3.如图,△ABC中,∠A=36°,D在边AC上,AD=BD=BC,求∠DBC的度数.
[任务二 探究等边三角形的性质]
活动3:在等腰三角形中,还有一类更特殊的三角形,底边和腰相等的三角形--等边三角形.
问题1:由于等边三角形是特殊的等腰三角形,那么等边三角形肯定也是轴对称图形,那它的对称轴有几条呢 为什么?
问题2:等腰三角形所具有的三线合一的性质,等边三角形也具有这个性质吗?
问题3:等腰三角形具有“等边对等角”性质,等边三角形中具有这样的性质吗?它的三个角有什么特征?
归纳总结:
1.等边三角形是 图形,它有 对称轴.
2.等边三角形的 、底边上的 、底边上的 重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴。
3.等边三角形的三个内角相等,都等于 。
例2已知,如图,P,Q是△ABC边BC上两点,且BP=PQ=QC=AP=AQ,求∠BAC的度数.
[即时测评]
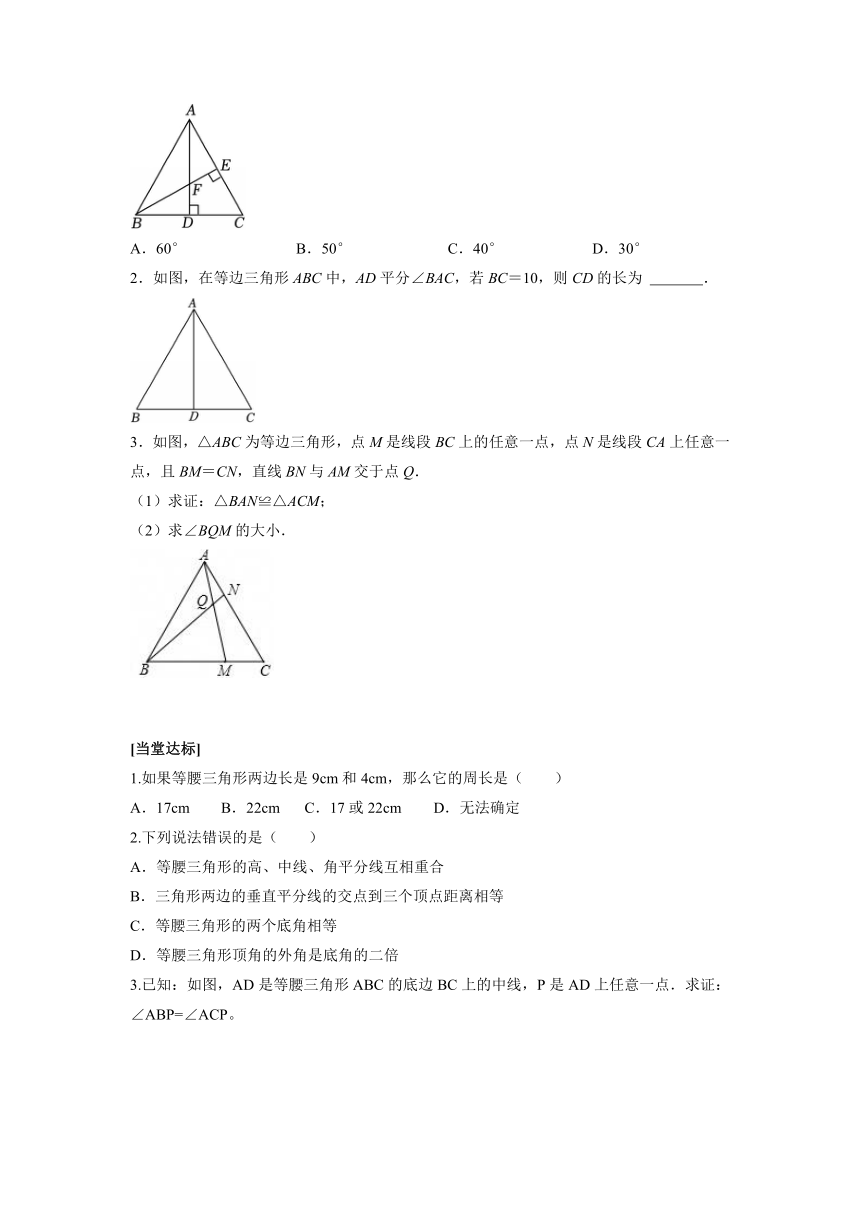
1.如图,在等边△ABC中,AD⊥BC,BE⊥AC,AD,BE交于点F,则∠AFE的度数是( )
A.60° B.50° C.40° D.30°
2.如图,在等边三角形ABC中,AD平分∠BAC,若BC=10,则CD的长为 .
3.如图,△ABC为等边三角形,点M是线段BC上的任意一点,点N是线段CA上任意一点,且BM=CN,直线BN与AM交于点Q.
(1)求证:△BAN≌△ACM;
(2)求∠BQM的大小.
[当堂达标]
1.如果等腰三角形两边长是9cm和4cm,那么它的周长是( )
A.17cm B.22cm C.17或22cm D.无法确定
2.下列说法错误的是( )
A.等腰三角形的高、中线、角平分线互相重合
B.三角形两边的垂直平分线的交点到三个顶点距离相等
C.等腰三角形的两个底角相等
D.等腰三角形顶角的外角是底角的二倍
3.已知:如图,AD是等腰三角形ABC的底边BC上的中线,P是AD上任意一点.求证:∠ABP=∠ACP。
4.如图所示的三角测平架中,AB=AC,在BC的中点D挂一个重锤,自然下垂,整架身,使点A恰好在重锤线上,试问:此时BC是否正好处于水平位置?为什么?
5.如图,△ABC、△ADE是等边三角形,B、C、D在同一直线上.试说明:
(1)CE=AC+DC;
(2)∠ECD=60°.
答案:
[任务一 探究等腰三角形的性质]
活动1:(1)腰 底边 (2)顶角 (3)底角
活动2:问题1:等腰三角形是轴对称图形,相等的线段:AB=AC、BD=CD;相等的角:∠B=∠C,∠BAD=∠CAD.
问题2:对折的折痕是它的对称轴,即线段BC的垂直平分线是对称轴.
问题3:我们沿着角平分线对折,等腰三角形能够完全重合,这说明,顶角平分线所在的直线是等腰三角形的对称轴.
问题4:底边上的中线所在的直线是等腰三角形的对称轴.底边上的高所在的直线是等腰三角形的对称轴.
问题5:你认为等腰三角形有哪些特征?与同伴进行交流.
1.等腰三角形是轴对称图形
2.等腰三角形的顶角平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴。
3.等腰三角形的两个底角相等。
例1 解:设这个等腰三角形顶角的应数为x,则底角的度数为2x。
根据“三角形三个内角的和等于180°”,得
X+2x+2x=180°
解得x=36°,
2x=72°,
所以。这个三角形的三个内角分别是36°,72°、72°.
[即时测评]
1.C
2.50°
3.解:∵BD=AD,
∴∠A=∠ABD=36°,
∴∠BDC=∠A+∠ABD=72°,
∵BD=BC,
∴∠BDC=∠BCD=72°,
∴∠DBC=180°﹣72°﹣72°=36°.
[任务二 探究等边三角形的性质]
活动3:问题1:由于等边三角形的三边都是相等的,因此,无论从哪个角进行对折,都是重合的,因此,等边三角形有三条对称轴.
问题2:等边三角形页具有“三线合一”的性质.
问题3:它的三个角都是相等的,都为60°
归纳总结:
1.轴对称 三条
2. 顶角平分线 中线 高
3. 60°
例2解:∵BP=PQ=QC=AP=AQ,
∴∠PAQ=∠APQ=∠AQP=60°,∠B=∠BAP,∠C=∠CAQ.
又∵∠BAP+∠ABP=∠APQ,∠C+∠CAQ=∠AQP,
∴∠BAP=∠CAQ=30°.
∴∠BAC=120°.
故∠BAC的度数是120°.
[即时测评]
1.A
2.5
3.解:(1)∵△ABC为等边三角形,
∴AB=BC=CA,∠BAC=∠BCA=60°,
∵BM=CN,
∴CM=AN,
又∵∠BAN=∠ACM,
∴△BAN≌△ACM;
(2)∴∠CAM=∠ABN,
∴∠BQM=∠ABN+∠BAQ=∠CAM+∠BAQ=∠BAC=60°.
[当堂达标]
1.B
2.A
3.证明:∵△ABC中,AB=AC,AD为BC边的中线,
∴AD是角平分线,
∴∠BAP=∠CAP,
在△ABP与△ACP中,
∴△ABP≌△ACP(SAS),
∴∠ABP=∠ACP。
4.解:这时BC处于水平位置.
∵D是BC的中点,
∴BD=DC,
∵AB=AC,
∴AD⊥BC(三线合一).
∵重锤线与地平线垂直,
∴BC处于水平位置。
5.解:(1)∵△ABC、△ADE是等边三角形,
∴AE=AD,BC=AC=AB,∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴BD=EC,
∵BD=BC+CD=AC+CD,
∴CE=BD=AC+CD;
(2)由(1)知:△BAD≌△CAE,
∴∠ACE=∠ABD=60°,
∴∠ECD=180°﹣∠ACB﹣∠ACE=60°,
∴∠ECD=60°.
第3课时 等腰三角形的性质
[学习目标]
1.探索并了解等腰三角形的性质;
2.知道等边三角形是特殊的等腰三角形,并掌握其性质.
3.在探索轴对称性质的过程中,能够进行有条理地思考并进行简单地推理.
[复习回顾]
观察下列各种图形,判断是不是轴对称图形,能找出对称轴吗?
[新知探究]
[任务一 探究等腰三角形的性质]
活动1:回顾等腰三角形中,有这样几个重要的概念:
(1)相等的两条边都叫 ;另一边叫 ;
(2)两腰的夹角∠A叫 ;
(3)腰与底边夹角∠B,∠C叫 .
活动2:同学们各自画一个等腰三角形,并动手将各自手中的三角形标上A,B,C.
将等腰三角形ABC纸板沿直线对折,我们将对折的痕迹标上AD.
问题1:结合我们之前学习的轴对称图形的意义,等腰三角形是轴对称图形吗 如果是,你能发现哪些相等的线段和相等的角?
问题2:等腰三角形的对称轴是一条怎样的直线?你是如何描述的?
问题3:顶角的平分线所在的直线是等腰三角形的对称轴吗 为什么?
问题4:底边上的中线所在的直线是等腰三角形的对称轴吗 底边上的高所在的直线呢
问题5:你认为等腰三角形有哪些特征?与同伴进行交流.
总结归纳:
1.等腰三角形是轴对称图形
2.等腰三角形的顶角平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴。
3.等腰三角形的两个底角相等。
例1 已知一个等腰三角形的底角是顶角的2倍,求它的各个内角的度。
[即时测评]
1.如图,在△ABC中,AB=AC,∠B=40°,AC的垂直平分线DE分别交AC,BC于点D,E,则∠BAE的度数为( )
A.50° B.40° C.60° D.80°
2.如图,在△ABC中,AB=AC,∠B=70°,AD是BC边上的中线,E是AC边上一点.若DE=DC,则∠ADE的度数为 .
3.如图,△ABC中,∠A=36°,D在边AC上,AD=BD=BC,求∠DBC的度数.
[任务二 探究等边三角形的性质]
活动3:在等腰三角形中,还有一类更特殊的三角形,底边和腰相等的三角形--等边三角形.
问题1:由于等边三角形是特殊的等腰三角形,那么等边三角形肯定也是轴对称图形,那它的对称轴有几条呢 为什么?
问题2:等腰三角形所具有的三线合一的性质,等边三角形也具有这个性质吗?
问题3:等腰三角形具有“等边对等角”性质,等边三角形中具有这样的性质吗?它的三个角有什么特征?
归纳总结:
1.等边三角形是 图形,它有 对称轴.
2.等边三角形的 、底边上的 、底边上的 重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴。
3.等边三角形的三个内角相等,都等于 。
例2已知,如图,P,Q是△ABC边BC上两点,且BP=PQ=QC=AP=AQ,求∠BAC的度数.
[即时测评]
1.如图,在等边△ABC中,AD⊥BC,BE⊥AC,AD,BE交于点F,则∠AFE的度数是( )
A.60° B.50° C.40° D.30°
2.如图,在等边三角形ABC中,AD平分∠BAC,若BC=10,则CD的长为 .
3.如图,△ABC为等边三角形,点M是线段BC上的任意一点,点N是线段CA上任意一点,且BM=CN,直线BN与AM交于点Q.
(1)求证:△BAN≌△ACM;
(2)求∠BQM的大小.
[当堂达标]
1.如果等腰三角形两边长是9cm和4cm,那么它的周长是( )
A.17cm B.22cm C.17或22cm D.无法确定
2.下列说法错误的是( )
A.等腰三角形的高、中线、角平分线互相重合
B.三角形两边的垂直平分线的交点到三个顶点距离相等
C.等腰三角形的两个底角相等
D.等腰三角形顶角的外角是底角的二倍
3.已知:如图,AD是等腰三角形ABC的底边BC上的中线,P是AD上任意一点.求证:∠ABP=∠ACP。
4.如图所示的三角测平架中,AB=AC,在BC的中点D挂一个重锤,自然下垂,整架身,使点A恰好在重锤线上,试问:此时BC是否正好处于水平位置?为什么?
5.如图,△ABC、△ADE是等边三角形,B、C、D在同一直线上.试说明:
(1)CE=AC+DC;
(2)∠ECD=60°.
答案:
[任务一 探究等腰三角形的性质]
活动1:(1)腰 底边 (2)顶角 (3)底角
活动2:问题1:等腰三角形是轴对称图形,相等的线段:AB=AC、BD=CD;相等的角:∠B=∠C,∠BAD=∠CAD.
问题2:对折的折痕是它的对称轴,即线段BC的垂直平分线是对称轴.
问题3:我们沿着角平分线对折,等腰三角形能够完全重合,这说明,顶角平分线所在的直线是等腰三角形的对称轴.
问题4:底边上的中线所在的直线是等腰三角形的对称轴.底边上的高所在的直线是等腰三角形的对称轴.
问题5:你认为等腰三角形有哪些特征?与同伴进行交流.
1.等腰三角形是轴对称图形
2.等腰三角形的顶角平分线、底边上的中线、底边上的高重合(也称“三线合一”),它们所在的直线都是等腰三角形的对称轴。
3.等腰三角形的两个底角相等。
例1 解:设这个等腰三角形顶角的应数为x,则底角的度数为2x。
根据“三角形三个内角的和等于180°”,得
X+2x+2x=180°
解得x=36°,
2x=72°,
所以。这个三角形的三个内角分别是36°,72°、72°.
[即时测评]
1.C
2.50°
3.解:∵BD=AD,
∴∠A=∠ABD=36°,
∴∠BDC=∠A+∠ABD=72°,
∵BD=BC,
∴∠BDC=∠BCD=72°,
∴∠DBC=180°﹣72°﹣72°=36°.
[任务二 探究等边三角形的性质]
活动3:问题1:由于等边三角形的三边都是相等的,因此,无论从哪个角进行对折,都是重合的,因此,等边三角形有三条对称轴.
问题2:等边三角形页具有“三线合一”的性质.
问题3:它的三个角都是相等的,都为60°
归纳总结:
1.轴对称 三条
2. 顶角平分线 中线 高
3. 60°
例2解:∵BP=PQ=QC=AP=AQ,
∴∠PAQ=∠APQ=∠AQP=60°,∠B=∠BAP,∠C=∠CAQ.
又∵∠BAP+∠ABP=∠APQ,∠C+∠CAQ=∠AQP,
∴∠BAP=∠CAQ=30°.
∴∠BAC=120°.
故∠BAC的度数是120°.
[即时测评]
1.A
2.5
3.解:(1)∵△ABC为等边三角形,
∴AB=BC=CA,∠BAC=∠BCA=60°,
∵BM=CN,
∴CM=AN,
又∵∠BAN=∠ACM,
∴△BAN≌△ACM;
(2)∴∠CAM=∠ABN,
∴∠BQM=∠ABN+∠BAQ=∠CAM+∠BAQ=∠BAC=60°.
[当堂达标]
1.B
2.A
3.证明:∵△ABC中,AB=AC,AD为BC边的中线,
∴AD是角平分线,
∴∠BAP=∠CAP,
在△ABP与△ACP中,
∴△ABP≌△ACP(SAS),
∴∠ABP=∠ACP。
4.解:这时BC处于水平位置.
∵D是BC的中点,
∴BD=DC,
∵AB=AC,
∴AD⊥BC(三线合一).
∵重锤线与地平线垂直,
∴BC处于水平位置。
5.解:(1)∵△ABC、△ADE是等边三角形,
∴AE=AD,BC=AC=AB,∠BAC=∠DAE=60°,
∴∠BAC+∠CAD=∠DAE+∠CAD,
即∠BAD=∠CAE,
∴△BAD≌△CAE(SAS),
∴BD=EC,
∵BD=BC+CD=AC+CD,
∴CE=BD=AC+CD;
(2)由(1)知:△BAD≌△CAE,
∴∠ACE=∠ABD=60°,
∴∠ECD=180°﹣∠ACB﹣∠ACE=60°,
∴∠ECD=60°.
