2.2 第4课时 等腰三角形的判定及含30°角的直角三角形的性质 导学案(含答案) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 2.2 第4课时 等腰三角形的判定及含30°角的直角三角形的性质 导学案(含答案) 2025-2026学年数学鲁教版(五四制)七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 292.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-19 13:34:49 | ||
图片预览


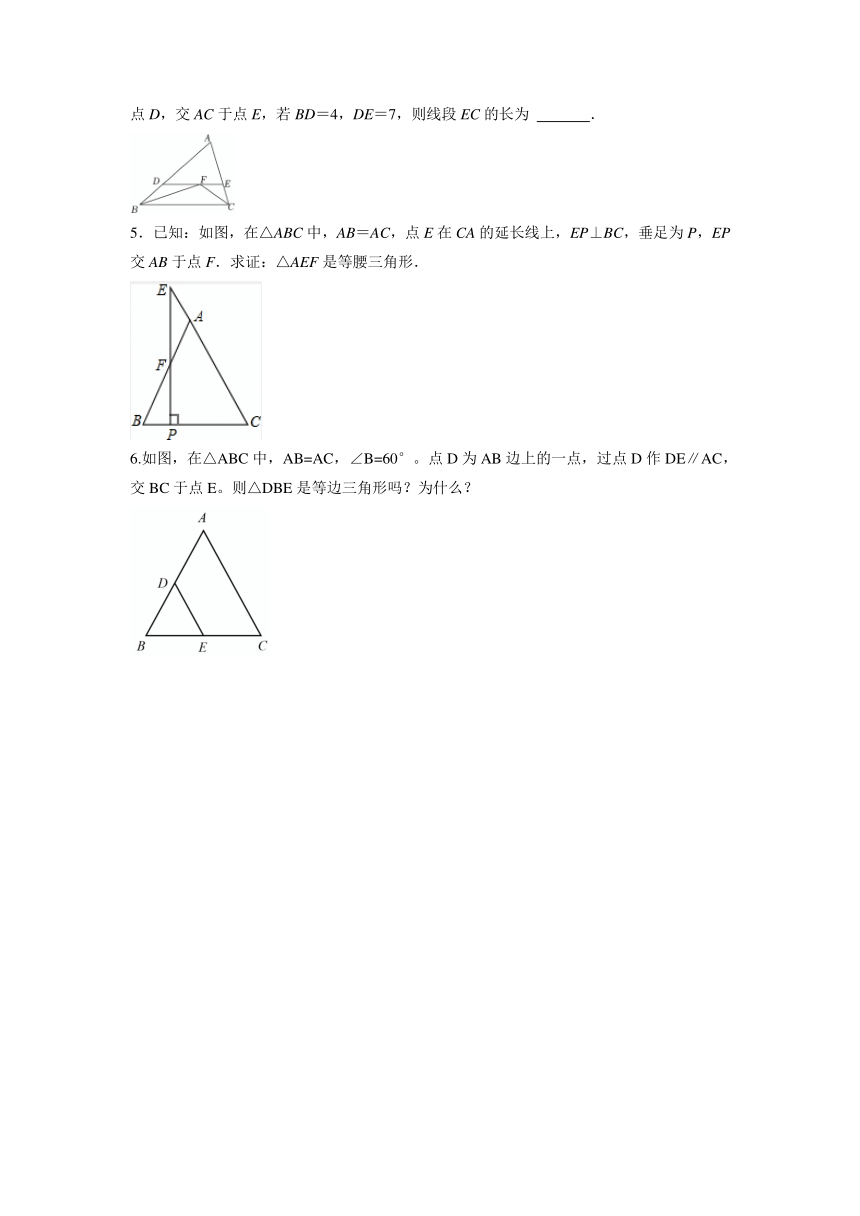
文档简介
2 简单的轴对称图形
第4课时 等腰三角形的判定及含30°角的直角三角形的性质
[学习目标]
1.掌握等腰三角形和等边三角形的性质及判定方法。
2.认识和探索含30°角的直角三角形的性质。
3.会综合运用等腰三角形的性质和判定进行有关的计算和推理。
[新知探究]
[任务一 探究等腰三角形的判定]
活动1:把“等腰三角形的两个底角相等”改写成“如果------那么-----”形式。
学生:如果___________,那么___________。
问题1:如图,在ΔABC中,如果∠B=∠C,AD是BC边上的高,那么△ABD与△ACD全等吗?边AB与AC相等吗?说明理由.
问题2:通过以上证明,你得到什么结论?
总结归纳:等腰三角形的判定:
例1 如图,已知AD∥BC,BD是∠ABC的平分线,那么△ABD是等腰三角形吗 为什么
[即时测评]
1.在△ABC中,已知,∠B=∠C,则( )
A.AB=BC B.AB=AC C.BC=AC D.∠A=60°
2.如图,若∠B=72°,∠C=36°,AD平分∠BAC,则图中共有 个等腰三角形.
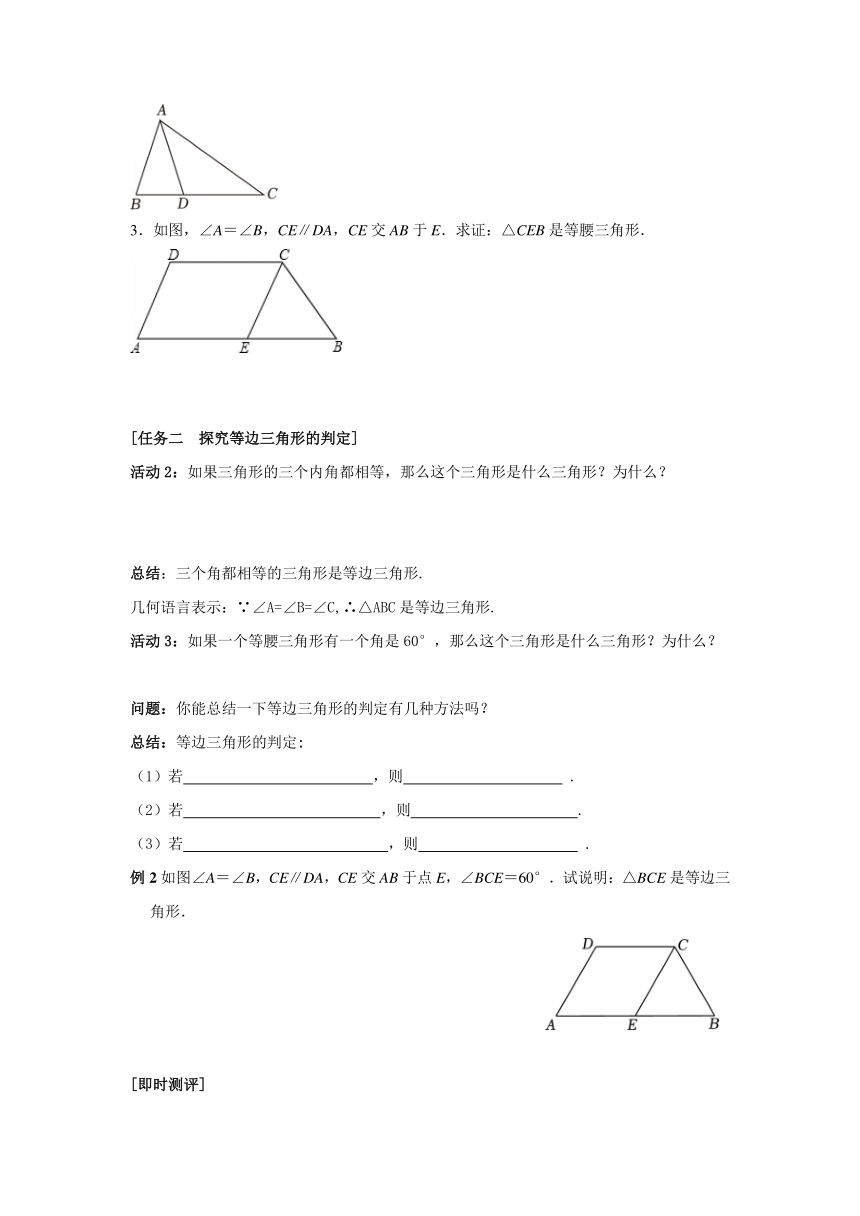
3.如图,∠A=∠B,CE∥DA,CE交AB于E.求证:△CEB是等腰三角形.
[任务二 探究等边三角形的判定]
活动2:如果三角形的三个内角都相等,那么这个三角形是什么三角形?为什么?
总结:三个角都相等的三角形是等边三角形.
几何语言表示:∵∠A=∠B=∠C,∴△ABC是等边三角形.
活动3:如果一个等腰三角形有一个角是60°,那么这个三角形是什么三角形?为什么?
问题:你能总结一下等边三角形的判定有几种方法吗?
总结:等边三角形的判定:
(1)若 ,则 .
(2)若 ,则 .
(3)若 ,则 .
例2如图∠A=∠B,CE∥DA,CE交AB于点E,∠BCE=60°.试说明:△BCE是等边三角形.
[即时测评]
1.下列条件中,能说明△ABC为等边三角形的是( )
A.∠A=60° B.∠B=60°,AB=AC
C.∠B+∠C=120° D.AB=AC
2.若△ABC,∠B=∠C,请添加一个条件使△ABC是等边三角形,则添加的条件可以是 .(写出一个即可)
3.如图,在△ABC中,D为AB边上一点,DF⊥BC于点F,延长FD、CA交于点E.若∠E=30°,AD=AE.求证:△ABC为等边三角形.
[任务三 探究30°角直角三角形的性质]
活动4:如图,将两个大小相同的含30°角的三角尺摆放在一起,所拼成的△ABD是什么三角形?
问题1:你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
问题2:在小组内交流,说出理由.你能得到什么结论?
结论: 含30°角的直角三角形的性质:
几何语言:∵ ,
∴
例3 如图,△ABC是等边三角形,D是BC边上一点,DE⊥AC于点E.若EC=3,则DC的长为( )
A.4 B.5 C.6 D.7
[即时测评]
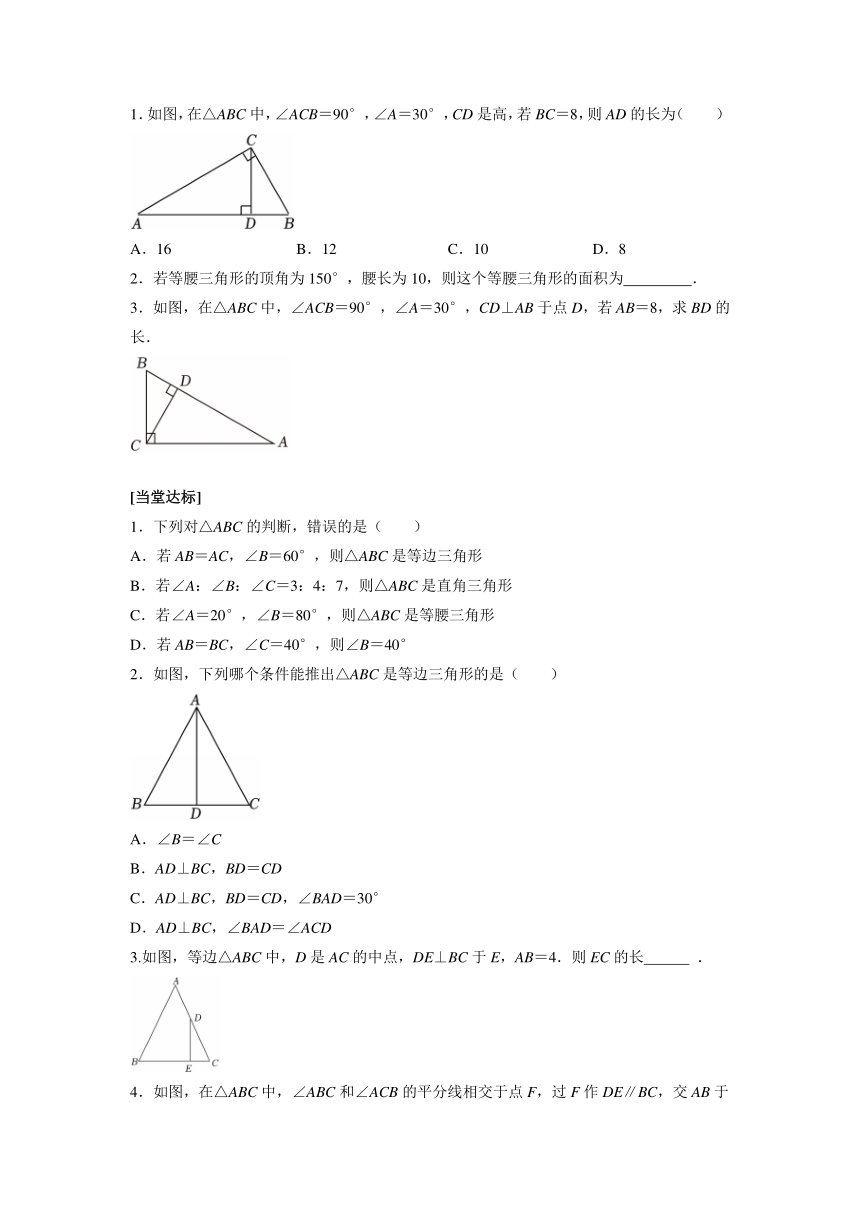
1.如图,在△ABC中,∠ACB=90°,∠A=30°,CD是高,若BC=8,则AD的长为( )
A.16 B.12 C.10 D.8
2.若等腰三角形的顶角为150°,腰长为10,则这个等腰三角形的面积为 .
3.如图,在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D,若AB=8,求BD的长.
[当堂达标]
1.下列对△ABC的判断,错误的是( )
A.若AB=AC,∠B=60°,则△ABC是等边三角形
B.若∠A:∠B:∠C=3:4:7,则△ABC是直角三角形
C.若∠A=20°,∠B=80°,则△ABC是等腰三角形
D.若AB=BC,∠C=40°,则∠B=40°
2.如图,下列哪个条件能推出△ABC是等边三角形的是( )
A.∠B=∠C
B.AD⊥BC,BD=CD
C.AD⊥BC,BD=CD,∠BAD=30°
D.AD⊥BC,∠BAD=∠ACD
3.如图,等边△ABC中,D是AC的中点,DE⊥BC于E,AB=4.则EC的长 .
4.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E,若BD=4,DE=7,则线段EC的长为 .
5.已知:如图,在△ABC中,AB=AC,点E在CA的延长线上,EP⊥BC,垂足为P,EP交AB于点F.求证:△AEF是等腰三角形.
6.如图,在△ABC中,AB=AC,∠B=60°。点D为AB边上的一点,过点D作DE∥AC,交BC于点E。则△DBE是等边三角形吗?为什么?
答案:
[任务一 探究等腰三角形的判定]
活动1:一个三角形是等腰三角形 它的两个底角相等
问题1:△ABD≌△ACD,AB=AC.
解:因为AD是BC边上的高,
所以AD⊥BC,
所以∠ADB=∠ADC,
因为∠B=∠C,AD=AD,
所以△ABD≌△ACD(AAS),
所以AB=AC(全等三角形对应边相等) .
问题2:如果一个三角形有两个底角相等,那么它们所对的边也相等。
例1 解:△ABD是等腰三角形,
理由是:
∵BD是∠ABC的平分线
∴∠ABD=∠DBC
又∵AD∥BC
∴∠ADB=∠DBC(两直线平等,内错角相等)
∴∠ADB=∠ABD
∴△ABD是等腰三角形.
[即时测评]
1.B
2.3
3.证明:∵CE∥DA,
∴∠A=∠CEB.
又∵∠A=∠B,
∴∠CEB=∠B.
∴CE=CB.
∴△CEB是等腰三角形.
[任务二 探究等边三角形的判定]
活动2:
解: ∵∠A=∠B,
∴BC=AC.
∵∠B=∠C,
∴AC=AB.
∴AB=BC=AC,
∴△ABC是等边三角形.
活动3:
解:(1)顶角是60°.
∵AB=AC,
∴∠C=∠B.
在△ABC中,∠A+∠B+∠C=180°
∵∠A=60°,
∴∠A=∠B=∠C=60°.
∴△ABC是等边三角形
(2)底角是60°.
解:∵AB=AC,
∴∠C=∠B=60°
在△ABC中,∠A+∠B+∠C=180°
∴∠A=60°,
∴∠A=∠B=∠C=60°
∴△ABC是等边三角形
问题:你能总结一下等边三角形的判定有几种方法吗?
总结:等边三角形的判定:
(1)若 三条边相等 ,则 三角形是等边三角形 .
(2)若 三个内角都相等的三角形 ,则 三角形是等边三角形 .
(3)若 有一个角是60°的等腰三角形 ,则 三角形是等边三角形 .
例2 解:∵CE∥DA,
∴∠A=∠CEB,
∵∠A=∠B,
∴∠CEB=∠B,
∴CB=CE;
又∵∠BCE=60°,
∴△BCE是等边三角形.
[即时测评]
1.B
2.∠A=∠B(答案不唯一).
3.证明:∵AD=AE,
∴∠E=∠ADE=30°,
∴∠CAB=∠E+∠ADE=30°+30°=60°,
∵DF⊥BC,
∴∠EFC=90°,
∴∠C=90°﹣∠E=60°,
∴∠B=180°﹣∠C﹣∠CAB=180°﹣60°﹣60°=60°,
∴∠C=∠B=∠CAB,
∴△ABC为等边三角形.
[任务三 探究30°角直角三角形的性质]
活动4: △ABD是等边三角形.
问题1:BC=AB或AB=2BC.
问题2:根据题意∠B=∠D=90°-30°=60°,
所以△ABD是等边三角形,
所以AB=BD=AD,
因为BC=CD,
所以BC=AB或AB=2BC.
结论: 在直角三角形中,如果一个锐角是30°,那么它所对的直角边等于斜边的一半。
2.几何语言:∵ Rt△ABC中,∠C=90°,∠A=30°,
∴ BC=AB或AB=2BC
例3 C
[即时测评]
1.B
2.25
3.解:∵∠ACB=90°,∠A=30°,AB=8
∴,∠B=60°,
∵CD⊥AB,
∴∠CDB=90°,
∴∠BCD=30°,
∴.
[当堂达标]
1.D
2.C
3.等边三角形.
4.3
5.证明:在△ABC中,
∵AB=AC,
∴∠B=∠C,
∵EP⊥BC,
∴∠C+∠E=90°,∠B+∠BFP=90°,
∴∠E=∠BFP,
又∵∠BFP=∠AFE,
∴∠E=∠AFE,
∴AF=AE,
∴△AEF是等腰三角形.
6.证明:∵AB=AC,∠B=60°
∴△ABC是等边三角形,
∴∠A=∠B=∠C=60°
又∵DE∥AC
∴∠BDE=∠A=60°,∠BED=∠C=60°
∴ ∠A=∠B=∠C= 60°
∴△ABC是等边三角形
第4课时 等腰三角形的判定及含30°角的直角三角形的性质
[学习目标]
1.掌握等腰三角形和等边三角形的性质及判定方法。
2.认识和探索含30°角的直角三角形的性质。
3.会综合运用等腰三角形的性质和判定进行有关的计算和推理。
[新知探究]
[任务一 探究等腰三角形的判定]
活动1:把“等腰三角形的两个底角相等”改写成“如果------那么-----”形式。
学生:如果___________,那么___________。
问题1:如图,在ΔABC中,如果∠B=∠C,AD是BC边上的高,那么△ABD与△ACD全等吗?边AB与AC相等吗?说明理由.
问题2:通过以上证明,你得到什么结论?
总结归纳:等腰三角形的判定:
例1 如图,已知AD∥BC,BD是∠ABC的平分线,那么△ABD是等腰三角形吗 为什么
[即时测评]
1.在△ABC中,已知,∠B=∠C,则( )
A.AB=BC B.AB=AC C.BC=AC D.∠A=60°
2.如图,若∠B=72°,∠C=36°,AD平分∠BAC,则图中共有 个等腰三角形.
3.如图,∠A=∠B,CE∥DA,CE交AB于E.求证:△CEB是等腰三角形.
[任务二 探究等边三角形的判定]
活动2:如果三角形的三个内角都相等,那么这个三角形是什么三角形?为什么?
总结:三个角都相等的三角形是等边三角形.
几何语言表示:∵∠A=∠B=∠C,∴△ABC是等边三角形.
活动3:如果一个等腰三角形有一个角是60°,那么这个三角形是什么三角形?为什么?
问题:你能总结一下等边三角形的判定有几种方法吗?
总结:等边三角形的判定:
(1)若 ,则 .
(2)若 ,则 .
(3)若 ,则 .
例2如图∠A=∠B,CE∥DA,CE交AB于点E,∠BCE=60°.试说明:△BCE是等边三角形.
[即时测评]
1.下列条件中,能说明△ABC为等边三角形的是( )
A.∠A=60° B.∠B=60°,AB=AC
C.∠B+∠C=120° D.AB=AC
2.若△ABC,∠B=∠C,请添加一个条件使△ABC是等边三角形,则添加的条件可以是 .(写出一个即可)
3.如图,在△ABC中,D为AB边上一点,DF⊥BC于点F,延长FD、CA交于点E.若∠E=30°,AD=AE.求证:△ABC为等边三角形.
[任务三 探究30°角直角三角形的性质]
活动4:如图,将两个大小相同的含30°角的三角尺摆放在一起,所拼成的△ABD是什么三角形?
问题1:你能借助这个图形,找到Rt△ABC的直角边BC与斜边AB之间的数量关系吗?
问题2:在小组内交流,说出理由.你能得到什么结论?
结论: 含30°角的直角三角形的性质:
几何语言:∵ ,
∴
例3 如图,△ABC是等边三角形,D是BC边上一点,DE⊥AC于点E.若EC=3,则DC的长为( )
A.4 B.5 C.6 D.7
[即时测评]
1.如图,在△ABC中,∠ACB=90°,∠A=30°,CD是高,若BC=8,则AD的长为( )
A.16 B.12 C.10 D.8
2.若等腰三角形的顶角为150°,腰长为10,则这个等腰三角形的面积为 .
3.如图,在△ABC中,∠ACB=90°,∠A=30°,CD⊥AB于点D,若AB=8,求BD的长.
[当堂达标]
1.下列对△ABC的判断,错误的是( )
A.若AB=AC,∠B=60°,则△ABC是等边三角形
B.若∠A:∠B:∠C=3:4:7,则△ABC是直角三角形
C.若∠A=20°,∠B=80°,则△ABC是等腰三角形
D.若AB=BC,∠C=40°,则∠B=40°
2.如图,下列哪个条件能推出△ABC是等边三角形的是( )
A.∠B=∠C
B.AD⊥BC,BD=CD
C.AD⊥BC,BD=CD,∠BAD=30°
D.AD⊥BC,∠BAD=∠ACD
3.如图,等边△ABC中,D是AC的中点,DE⊥BC于E,AB=4.则EC的长 .
4.如图,在△ABC中,∠ABC和∠ACB的平分线相交于点F,过F作DE∥BC,交AB于点D,交AC于点E,若BD=4,DE=7,则线段EC的长为 .
5.已知:如图,在△ABC中,AB=AC,点E在CA的延长线上,EP⊥BC,垂足为P,EP交AB于点F.求证:△AEF是等腰三角形.
6.如图,在△ABC中,AB=AC,∠B=60°。点D为AB边上的一点,过点D作DE∥AC,交BC于点E。则△DBE是等边三角形吗?为什么?
答案:
[任务一 探究等腰三角形的判定]
活动1:一个三角形是等腰三角形 它的两个底角相等
问题1:△ABD≌△ACD,AB=AC.
解:因为AD是BC边上的高,
所以AD⊥BC,
所以∠ADB=∠ADC,
因为∠B=∠C,AD=AD,
所以△ABD≌△ACD(AAS),
所以AB=AC(全等三角形对应边相等) .
问题2:如果一个三角形有两个底角相等,那么它们所对的边也相等。
例1 解:△ABD是等腰三角形,
理由是:
∵BD是∠ABC的平分线
∴∠ABD=∠DBC
又∵AD∥BC
∴∠ADB=∠DBC(两直线平等,内错角相等)
∴∠ADB=∠ABD
∴△ABD是等腰三角形.
[即时测评]
1.B
2.3
3.证明:∵CE∥DA,
∴∠A=∠CEB.
又∵∠A=∠B,
∴∠CEB=∠B.
∴CE=CB.
∴△CEB是等腰三角形.
[任务二 探究等边三角形的判定]
活动2:
解: ∵∠A=∠B,
∴BC=AC.
∵∠B=∠C,
∴AC=AB.
∴AB=BC=AC,
∴△ABC是等边三角形.
活动3:
解:(1)顶角是60°.
∵AB=AC,
∴∠C=∠B.
在△ABC中,∠A+∠B+∠C=180°
∵∠A=60°,
∴∠A=∠B=∠C=60°.
∴△ABC是等边三角形
(2)底角是60°.
解:∵AB=AC,
∴∠C=∠B=60°
在△ABC中,∠A+∠B+∠C=180°
∴∠A=60°,
∴∠A=∠B=∠C=60°
∴△ABC是等边三角形
问题:你能总结一下等边三角形的判定有几种方法吗?
总结:等边三角形的判定:
(1)若 三条边相等 ,则 三角形是等边三角形 .
(2)若 三个内角都相等的三角形 ,则 三角形是等边三角形 .
(3)若 有一个角是60°的等腰三角形 ,则 三角形是等边三角形 .
例2 解:∵CE∥DA,
∴∠A=∠CEB,
∵∠A=∠B,
∴∠CEB=∠B,
∴CB=CE;
又∵∠BCE=60°,
∴△BCE是等边三角形.
[即时测评]
1.B
2.∠A=∠B(答案不唯一).
3.证明:∵AD=AE,
∴∠E=∠ADE=30°,
∴∠CAB=∠E+∠ADE=30°+30°=60°,
∵DF⊥BC,
∴∠EFC=90°,
∴∠C=90°﹣∠E=60°,
∴∠B=180°﹣∠C﹣∠CAB=180°﹣60°﹣60°=60°,
∴∠C=∠B=∠CAB,
∴△ABC为等边三角形.
[任务三 探究30°角直角三角形的性质]
活动4: △ABD是等边三角形.
问题1:BC=AB或AB=2BC.
问题2:根据题意∠B=∠D=90°-30°=60°,
所以△ABD是等边三角形,
所以AB=BD=AD,
因为BC=CD,
所以BC=AB或AB=2BC.
结论: 在直角三角形中,如果一个锐角是30°,那么它所对的直角边等于斜边的一半。
2.几何语言:∵ Rt△ABC中,∠C=90°,∠A=30°,
∴ BC=AB或AB=2BC
例3 C
[即时测评]
1.B
2.25
3.解:∵∠ACB=90°,∠A=30°,AB=8
∴,∠B=60°,
∵CD⊥AB,
∴∠CDB=90°,
∴∠BCD=30°,
∴.
[当堂达标]
1.D
2.C
3.等边三角形.
4.3
5.证明:在△ABC中,
∵AB=AC,
∴∠B=∠C,
∵EP⊥BC,
∴∠C+∠E=90°,∠B+∠BFP=90°,
∴∠E=∠BFP,
又∵∠BFP=∠AFE,
∴∠E=∠AFE,
∴AF=AE,
∴△AEF是等腰三角形.
6.证明:∵AB=AC,∠B=60°
∴△ABC是等边三角形,
∴∠A=∠B=∠C=60°
又∵DE∥AC
∴∠BDE=∠A=60°,∠BED=∠C=60°
∴ ∠A=∠B=∠C= 60°
∴△ABC是等边三角形
