3.3 第2课时 勾股定理的实际应用(二) 导学案 (含答案) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 3.3 第2课时 勾股定理的实际应用(二) 导学案 (含答案) 2025-2026学年数学鲁教版(五四制)七年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 436.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-19 13:41:08 | ||
图片预览



文档简介
3 勾股定理的应用举例
第2课时 勾股定理的实际应用(二)
[学习目标]
1.能运用勾股定理解决古代数学问题.
2.能运用勾股定理及其逆定理解决生活中与梯子、折叠有关的实际问题.体会方程思想的运用.
[新知探究]
[任务一 探究古代数学问题]
例1今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深、葭长各几何.(选自《九章算术》)
题目大意:有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇沿垂直拉向岸边,那么它的顶端恰好到达岸边的水面.这个水池的水深和这根芦苇的长度各是多少
[即时测评]
1.明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地.送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千OA静止的时候,踏板离地高一尺(AC=1尺),将它往前推进两步(EB=10尺),此时踏板升高离地五尺(BD=5尺),求秋千绳索(OA或OB)的长度.
[任务二 探究利用“勾股定理模型”解实际问题]
例2如图,某单向隧道的截面是一个半径为4.2 m的半圆形,一辆高3.6 m、宽3 m的卡车能通过该隧道吗
问题1:请你能根据你对这个题的理解,画出卡车从隧道正中间通过时的示意图.
学生:通过交流、合作画出如图所示的示意图.
问题2:根据题意 你所画出的示意图中,各线段的长度分别是多少?
学生:由题意可知:车宽AB=3m,车高BC=4.2m.
问题3:需要求什么?如何判断卡车能不能通过该隧道.
学生:需要计算OC的长度,若OC的长度小于半径,卡车能通过,否则,卡车不能通过.
问题4:那如何计算OC的长度?
学生:可以利用勾股定理:= + ,计算.
[即时测评]
1.一辆装满货物,宽为2.4米的卡车,欲通过如图所示的隧道,则卡车的外形高必须低于( )
A.4.1米 B.4.0米 C.3.9米 D.3.8米
2.如图所示,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7m,顶端距离地面2.4m.如果保持梯子底端不动,将梯子斜靠在右墙时,顶端距离地面2m,那么小巷的宽度为( )
A.0.7m B.1.5m C.2.2m D.2.4m
3.如图所示,梯子AB靠在墙上,梯子的顶端A到墙根O的距离为24m,梯子的底端B到墙根O的距离为7m,一不小心梯子顶端A下滑了4米到C,底端B滑动到D,那么BD的长是 m.
4.春秋季节筑城广场放风筝已经成为贵阳市的一道亮丽风景线.某校八年级的两位同学学习了“勾股定理”之后,想要测得风筝的垂直高度CE,他们进行了如下操作:①测得水平距离BD的长为5米;②根据手中剩余线的长度计算出风等线BC的长为13米;③牵线放风筝的小明的身高为1.5米.
(1)求风筝的垂直高度CE;
(2)如果小明想让风筝沿CD方向下降2米,则他应该往回收线多少米?
[当堂达标]
1.如图,已知钓鱼竿AC的长为10m,露在水面上的鱼线BC长为6m,某钓鱼者想看看鱼钩上的情况,把鱼竿AC转动到AC'的位置,此时露在水面上的鱼线B'C'为8m,则BB'的长为( )
A.1m B.2m C.3m D.4m
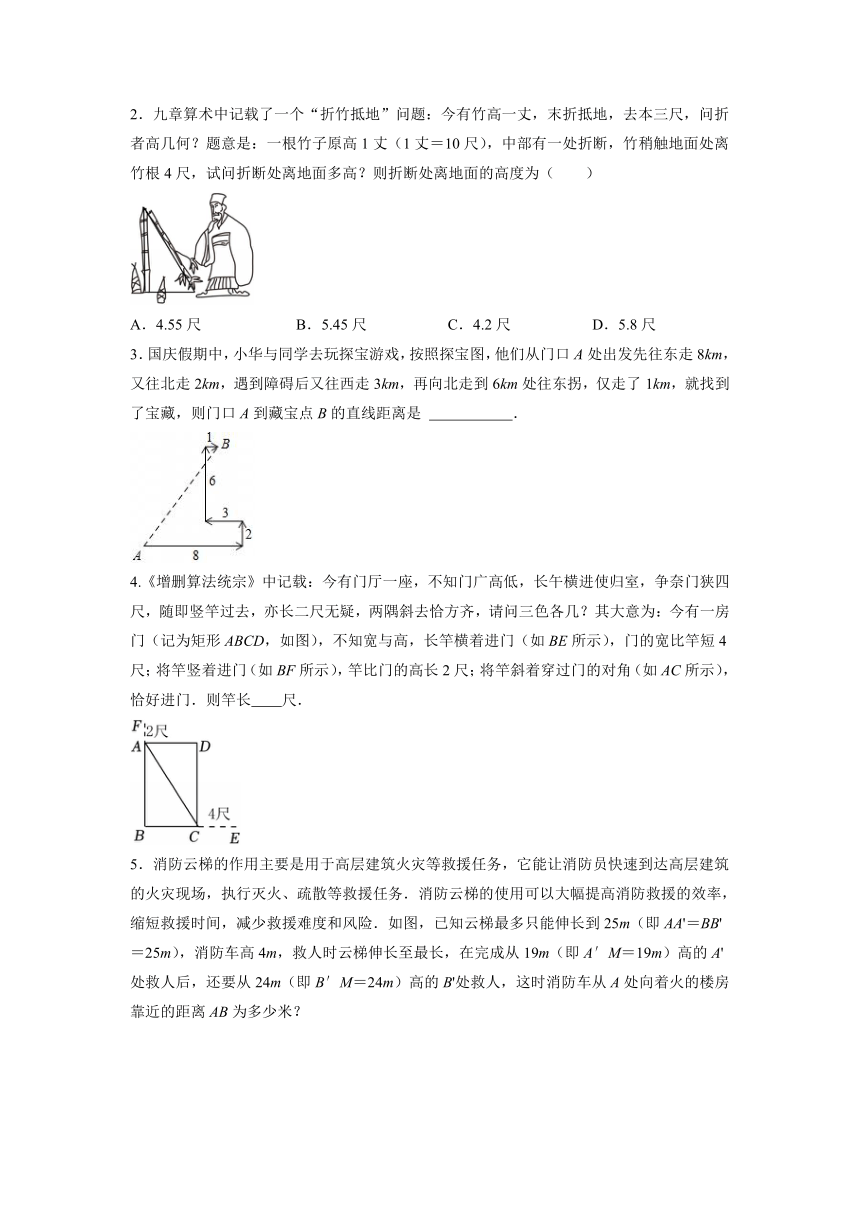
2.九章算术中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?题意是:一根竹子原高1丈(1丈=10尺),中部有一处折断,竹稍触地面处离竹根4尺,试问折断处离地面多高?则折断处离地面的高度为( )
A.4.55尺 B.5.45尺 C.4.2尺 D.5.8尺
3.国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口A处出发先往东走8km,又往北走2km,遇到障碍后又往西走3km,再向北走到6km处往东拐,仅走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是 .
4.《增删算法统宗》中记载:今有门厅一座,不知门广高低,长午横进使归室,争奈门狭四尺,随即竖竿过去,亦长二尺无疑,两隅斜去恰方齐,请问三色各几?其大意为:今有一房门(记为矩形ABCD,如图),不知宽与高,长竿横着进门(如BE所示),门的宽比竿短4尺;将竿竖着进门(如BF所示),竿比门的高长2尺;将竿斜着穿过门的对角(如AC所示),恰好进门.则竿长 尺.
5.消防云梯的作用主要是用于高层建筑火灾等救援任务,它能让消防员快速到达高层建筑的火灾现场,执行灭火、疏散等救援任务.消防云梯的使用可以大幅提高消防救援的效率,缩短救援时间,减少救援难度和风险.如图,已知云梯最多只能伸长到25m(即AA'=BB'=25m),消防车高4m,救人时云梯伸长至最长,在完成从19m(即A′M=19m)高的A'处救人后,还要从24m(即B′M=24m)高的B'处救人,这时消防车从A处向着火的楼房靠近的距离AB为多少米?
6.某工厂的大门如图所示,其中下方是高为2.3米、宽为2米的矩形,上方是半径为1米的半圆形.货车司机小王开着一辆高为3.0米,宽为1.6米的装满货物的卡车,能否进入如图所示的工厂大门?请说明你的理由.
答案:
任务一 探究古代数学问题
例1解:设水池的水深OA为x尺,则这根芦苇长OB为(x+1)尺,由于芦苇位于水池中央,所以AC为5尺,在Rt△OAC中,
由勾股定理得:
+ = ,
∴25+ = +2 x+1,
∴2 x=24,
∴ x=12, x+1=13
因此水池的水深12尺,这根芦苇长13尺。
即时测评
1.解:设OA=OB=x尺,
∵EC=BD=5尺,AC=1尺,
∴EA=EC﹣AC=5﹣1=4(尺),OE=OA﹣AE=(x﹣4)尺,
在Rt△OEB中,OE=(x﹣4)尺,OB=x尺,EB=10尺,
根据勾股定理得:x2=(x﹣4)2+102,
整理得:8x=116,即2x=29,
解得:x=14.5.
则秋千绳索的长度为14.5尺.
任务二 探究利用“勾股定理模型”解实际问题
例2解:隧道的横截面如图所示,AB的中点O是隧道的截面半圆的圆心。
OB=1.5m,BC=3.6m,∠ABC为直角,
在Rt△OBC中,由勾股定理,得= + ,
即:= + =15.21,
隧道的截面半径r=4.2m,>16>15.21,
所以卡车可以沿着隧道中间顺利通过。
即时测评
1.A
2.C
3.8
4.解:(1)由题意可知,∠CDB=90°,BD=5米,BC=13米,AB=DE=1.5米,
在Rt△CDB中,由勾股定理得:CD12(米),
∴CE=CD+DE=12+1.5=13.5(米),
答:风筝的垂直高度CE为13.5米;
(2)如图,CM=2米,连接BM,
∴DM=CD﹣CM=12﹣2=10(米),
在Rt△MDB中,由勾股定理得:BM5(米),
∴BC﹣BM=(13﹣5)(米),
∴他应该往回收线(13﹣5)米.
[当堂达标]
1.B
2.C
3.10km
4..
5.解:由题意可知,DM=4m,AA'=BB'=25m,A'M=19m,B′M=24m,AD⊥B′M,点A、B、D三点共线,
∴A'D=A'M﹣DM=19﹣4=15(m),B′D=B′M﹣DM=24﹣4=20(m),
在Rt△AA'D中,由勾股定理得:AD20(m),
在Rt△BB'D中,由勾股定理得:BD15(m),
∴AB=AD﹣BD=20﹣15=5(m).
答:这时消防车从A处向着火的楼房靠近的距离AB为5m.
6.解:设BB′与矩形的宽的交点为C,
∵AB=1米,AC=0.8米,∠ACB=90°,
∴BC0.6米,
∵BB′=BC+CB′=2.3+0.6=2.9<3.0,
∴不能通过.
第2课时 勾股定理的实际应用(二)
[学习目标]
1.能运用勾股定理解决古代数学问题.
2.能运用勾股定理及其逆定理解决生活中与梯子、折叠有关的实际问题.体会方程思想的运用.
[新知探究]
[任务一 探究古代数学问题]
例1今有池方一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深、葭长各几何.(选自《九章算术》)
题目大意:有一个水池,水面是一个边长为1丈的正方形,在水池正中央有一根新生的芦苇,它高出水面1尺.如果把这根芦苇沿垂直拉向岸边,那么它的顶端恰好到达岸边的水面.这个水池的水深和这根芦苇的长度各是多少
[即时测评]
1.明朝数学家程大位在他的著作《算法统宗》中写了一首计算秋千绳索长度的词《西江月》:“平地秋千未起,踏板一尺离地.送行二步恰竿齐,五尺板高离地…”翻译成现代文为:如图,秋千OA静止的时候,踏板离地高一尺(AC=1尺),将它往前推进两步(EB=10尺),此时踏板升高离地五尺(BD=5尺),求秋千绳索(OA或OB)的长度.
[任务二 探究利用“勾股定理模型”解实际问题]
例2如图,某单向隧道的截面是一个半径为4.2 m的半圆形,一辆高3.6 m、宽3 m的卡车能通过该隧道吗
问题1:请你能根据你对这个题的理解,画出卡车从隧道正中间通过时的示意图.
学生:通过交流、合作画出如图所示的示意图.
问题2:根据题意 你所画出的示意图中,各线段的长度分别是多少?
学生:由题意可知:车宽AB=3m,车高BC=4.2m.
问题3:需要求什么?如何判断卡车能不能通过该隧道.
学生:需要计算OC的长度,若OC的长度小于半径,卡车能通过,否则,卡车不能通过.
问题4:那如何计算OC的长度?
学生:可以利用勾股定理:= + ,计算.
[即时测评]
1.一辆装满货物,宽为2.4米的卡车,欲通过如图所示的隧道,则卡车的外形高必须低于( )
A.4.1米 B.4.0米 C.3.9米 D.3.8米
2.如图所示,小巷左右两侧是竖直的墙,一架梯子斜靠在左墙时,梯子底端到左墙角的距离为0.7m,顶端距离地面2.4m.如果保持梯子底端不动,将梯子斜靠在右墙时,顶端距离地面2m,那么小巷的宽度为( )
A.0.7m B.1.5m C.2.2m D.2.4m
3.如图所示,梯子AB靠在墙上,梯子的顶端A到墙根O的距离为24m,梯子的底端B到墙根O的距离为7m,一不小心梯子顶端A下滑了4米到C,底端B滑动到D,那么BD的长是 m.
4.春秋季节筑城广场放风筝已经成为贵阳市的一道亮丽风景线.某校八年级的两位同学学习了“勾股定理”之后,想要测得风筝的垂直高度CE,他们进行了如下操作:①测得水平距离BD的长为5米;②根据手中剩余线的长度计算出风等线BC的长为13米;③牵线放风筝的小明的身高为1.5米.
(1)求风筝的垂直高度CE;
(2)如果小明想让风筝沿CD方向下降2米,则他应该往回收线多少米?
[当堂达标]
1.如图,已知钓鱼竿AC的长为10m,露在水面上的鱼线BC长为6m,某钓鱼者想看看鱼钩上的情况,把鱼竿AC转动到AC'的位置,此时露在水面上的鱼线B'C'为8m,则BB'的长为( )
A.1m B.2m C.3m D.4m
2.九章算术中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?题意是:一根竹子原高1丈(1丈=10尺),中部有一处折断,竹稍触地面处离竹根4尺,试问折断处离地面多高?则折断处离地面的高度为( )
A.4.55尺 B.5.45尺 C.4.2尺 D.5.8尺
3.国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口A处出发先往东走8km,又往北走2km,遇到障碍后又往西走3km,再向北走到6km处往东拐,仅走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是 .
4.《增删算法统宗》中记载:今有门厅一座,不知门广高低,长午横进使归室,争奈门狭四尺,随即竖竿过去,亦长二尺无疑,两隅斜去恰方齐,请问三色各几?其大意为:今有一房门(记为矩形ABCD,如图),不知宽与高,长竿横着进门(如BE所示),门的宽比竿短4尺;将竿竖着进门(如BF所示),竿比门的高长2尺;将竿斜着穿过门的对角(如AC所示),恰好进门.则竿长 尺.
5.消防云梯的作用主要是用于高层建筑火灾等救援任务,它能让消防员快速到达高层建筑的火灾现场,执行灭火、疏散等救援任务.消防云梯的使用可以大幅提高消防救援的效率,缩短救援时间,减少救援难度和风险.如图,已知云梯最多只能伸长到25m(即AA'=BB'=25m),消防车高4m,救人时云梯伸长至最长,在完成从19m(即A′M=19m)高的A'处救人后,还要从24m(即B′M=24m)高的B'处救人,这时消防车从A处向着火的楼房靠近的距离AB为多少米?
6.某工厂的大门如图所示,其中下方是高为2.3米、宽为2米的矩形,上方是半径为1米的半圆形.货车司机小王开着一辆高为3.0米,宽为1.6米的装满货物的卡车,能否进入如图所示的工厂大门?请说明你的理由.
答案:
任务一 探究古代数学问题
例1解:设水池的水深OA为x尺,则这根芦苇长OB为(x+1)尺,由于芦苇位于水池中央,所以AC为5尺,在Rt△OAC中,
由勾股定理得:
+ = ,
∴25+ = +2 x+1,
∴2 x=24,
∴ x=12, x+1=13
因此水池的水深12尺,这根芦苇长13尺。
即时测评
1.解:设OA=OB=x尺,
∵EC=BD=5尺,AC=1尺,
∴EA=EC﹣AC=5﹣1=4(尺),OE=OA﹣AE=(x﹣4)尺,
在Rt△OEB中,OE=(x﹣4)尺,OB=x尺,EB=10尺,
根据勾股定理得:x2=(x﹣4)2+102,
整理得:8x=116,即2x=29,
解得:x=14.5.
则秋千绳索的长度为14.5尺.
任务二 探究利用“勾股定理模型”解实际问题
例2解:隧道的横截面如图所示,AB的中点O是隧道的截面半圆的圆心。
OB=1.5m,BC=3.6m,∠ABC为直角,
在Rt△OBC中,由勾股定理,得= + ,
即:= + =15.21,
隧道的截面半径r=4.2m,>16>15.21,
所以卡车可以沿着隧道中间顺利通过。
即时测评
1.A
2.C
3.8
4.解:(1)由题意可知,∠CDB=90°,BD=5米,BC=13米,AB=DE=1.5米,
在Rt△CDB中,由勾股定理得:CD12(米),
∴CE=CD+DE=12+1.5=13.5(米),
答:风筝的垂直高度CE为13.5米;
(2)如图,CM=2米,连接BM,
∴DM=CD﹣CM=12﹣2=10(米),
在Rt△MDB中,由勾股定理得:BM5(米),
∴BC﹣BM=(13﹣5)(米),
∴他应该往回收线(13﹣5)米.
[当堂达标]
1.B
2.C
3.10km
4..
5.解:由题意可知,DM=4m,AA'=BB'=25m,A'M=19m,B′M=24m,AD⊥B′M,点A、B、D三点共线,
∴A'D=A'M﹣DM=19﹣4=15(m),B′D=B′M﹣DM=24﹣4=20(m),
在Rt△AA'D中,由勾股定理得:AD20(m),
在Rt△BB'D中,由勾股定理得:BD15(m),
∴AB=AD﹣BD=20﹣15=5(m).
答:这时消防车从A处向着火的楼房靠近的距离AB为5m.
6.解:设BB′与矩形的宽的交点为C,
∵AB=1米,AC=0.8米,∠ACB=90°,
∴BC0.6米,
∵BB′=BC+CB′=2.3+0.6=2.9<3.0,
∴不能通过.
