4.1 无理数 导学案 (含答案) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 4.1 无理数 导学案 (含答案) 2025-2026学年数学鲁教版(五四制)七年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 107.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-19 13:41:21 | ||
图片预览


文档简介
1无理数
[学习目标]
1.通过拼图活动,感受无理数产生的实际背景和引入的必要性.
2.借助计算器探索无理数是无限不循环小数并从中体会无限逼近的思想.
3.会判断一个数是有理数还是无理数.
[复习回顾]
1. 一个整数的平方一定是整数吗?
2. 一个分数的平方一定是分数吗?
[新知探究]
[任务一 探究不是有理数的数]
活动1:让学生用准备好的两个边长为1的正方形纸片,剪一剪,拼一拼,设法得到一个小的正方形。
学生可能出现的拼图结果:
问题1:(1)设大正方形的边长为a, a满足什么条件?
问题2:a可能是整数吗?说说你的理由。
问题3:a可能是分数吗?说说你的理由。
结论:a既不是整数,也不是分数,所以a不是有理数。
例1如图:(1)以直角三角形的斜边为边的正方形的面积是多少?(小正方形边长为1,中正方形边长为2)
(2)设该正方形的边长为b,b满足什么条件?
(3)b是有理数吗?
[即时测评]
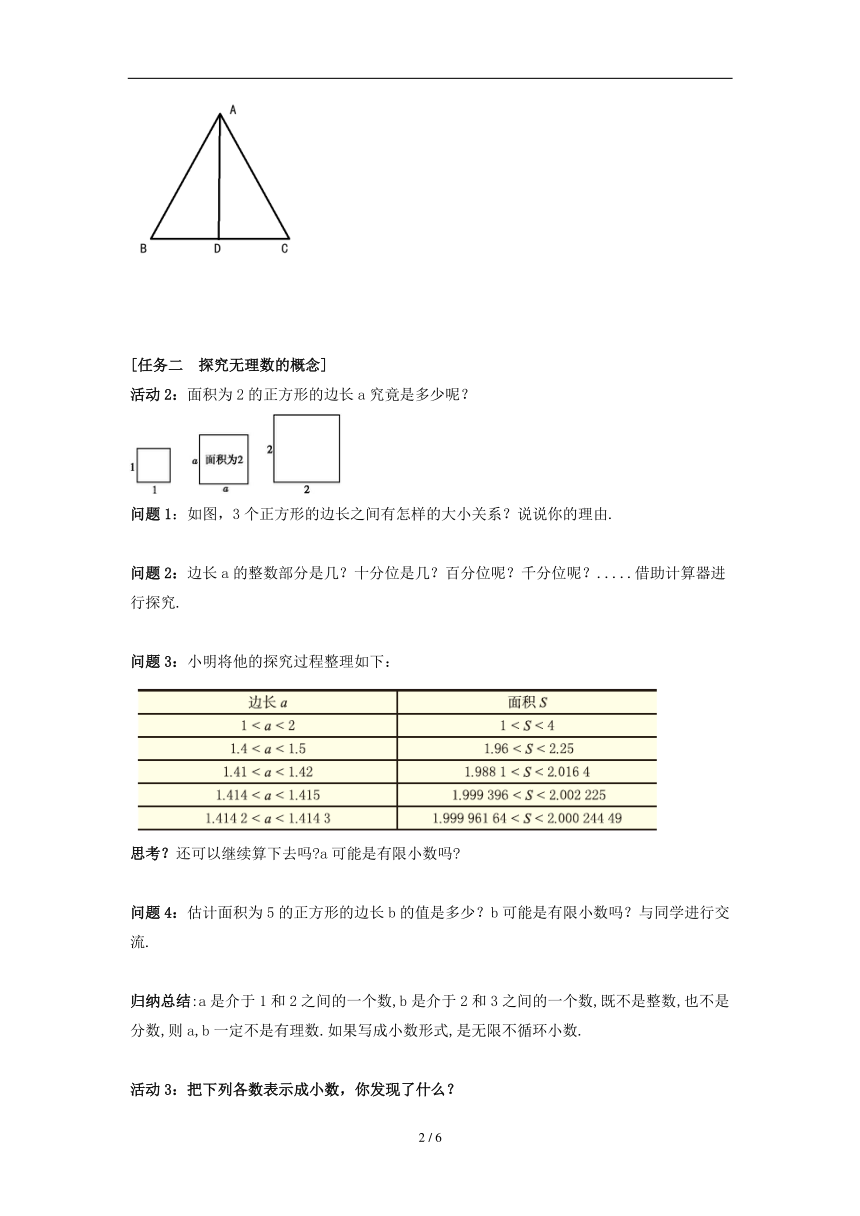
1.如图,等边三角形的边长为2,高为h,h可能是整数吗?可能是分数吗?是有理数吗?
[任务二 探究无理数的概念]
活动2:面积为2的正方形的边长a究竟是多少呢?
问题1:如图,3个正方形的边长之间有怎样的大小关系?说说你的理由.
问题2:边长a的整数部分是几?十分位是几?百分位呢?千分位呢?.....借助计算器进行探究.
问题3:小明将他的探究过程整理如下:
思考?还可以继续算下去吗 a可能是有限小数吗
问题4:估计面积为5的正方形的边长b的值是多少?b可能是有限小数吗?与同学进行交流.
归纳总结:a是介于1和2之间的一个数,b是介于2和3之间的一个数,既不是整数,也不是分数,则a,b一定不是有理数.如果写成小数形式,是无限不循环小数.
活动3:把下列各数表示成小数,你发现了什么?
教师:有理数总可以用有限小数或无限循环小数表示.反过来,任何有限小数或无限循环小数也都是有理数.
教师:无限不循环小数称为无理数.
例2下列各数中,哪些是有理数 哪些是无理数
3.14,﹣,0.,0.101 000 100 000 1…(相邻两个1之间0的个数逐次加2).
[即时测评]
1.在下列数:﹣2.5,,0,﹣1.121121112…,,﹣π中,无理数有( )
A.1个 B.2个 C.3个 D.4个
2.在数﹣65,,3.14,0,,﹣π,0.020020002…中,无理数共有 个.
3.如图,△ABC中,∠C=90°,BC=4,AC=3,点P在线段AC上,若BP的长度是个无理数,则BP的长度可以是 .(写出一个即可)
[当堂达标]
1.的大小在两个相邻整数之间,这两个整数是( )
A.1和2 B.2和3 C.3和4 D.4和5
2.下列实数是无理数的是( )
A.﹣2025 B.π C.3.14159 D.
3以下各正方形的边长是无理数的是( )
A.面积为25的正方形;
B.面积为的正方形;
C.面积为8的正方形;
D.面积为1.44的正方形.
4.下列各数中:12,,,﹣|﹣1|,0.1010010001…(每两个1之间的0依次加1),其中,无理数有 个.
5.已知直角三角形的两直角边长分别是9 cm和5 cm,斜边长是x cm.
(1)估计x在哪两个连续整数之间;
(2)如果把x的结果精确到0.1,估计x的值;如果精确到 0.01 呢?
答案:
[任务一 探究不是有理数的数]
活动1:
问题1:因为 S大正方形 = 2,所以 = 2.
问题2:(1)如图:因为 = 2,而 = 1, = 4,
所以 < < .
所以 1< a < 2,故 a 不是整数.
(2)如图:在△ABC中,AC=1,AC=1,BC=a
根据三角形的三边关系: AB-AC< a所以0问题3:a不是分数,理由:假设a是分母为2的分数,则= <2,
=>2,所以,不可能是分母为2的分数,其它的依次类推......
结论:a既不是整数,也不是分数,所以a不是有理数。
例1
解:(1)以直角三角形的斜边为边的正方形的面积为+=5;
(2)根据三角形的三边关系可得:1<b<3;
(3)b不是有理数.
[即时测评]
1.解:因为三角形是等边三角形,且AD⊥BC,
所以BD=DC,则BD=AB=1,
根据勾股定理得:
h不可能是整数;h也不可能是分数,也不是有理数.
[任务二 探究无理数的概念]
活动2:
问题1:1<a<2
问题2:边长a的整数部分是1,十分位是4,百分位是1,千分位是4.
问题3:a=1.414 213 56…, 它不可能是一个有限小数.
问题4:b=2.236067977···,不可能是有限小数.
归纳总结:a是介于1和2之间的一个数,b是介于2和3之间的一个数,既不是整数,也不是分数,则a,b一定不是有理数.如果写成小数形式,是无限不循环小数.
活动3:
例2
解:有理数有:3.14,﹣,0.;
无理数有:0.101 000 100 000 1…(相邻两个1之间0的个数逐次加2).
[即时测评]
1.B
2.2
3.(答案不唯一)
[当堂达标]
1.C
2.B
3.C
4.2
5.解:(1)根据题意,可得x2=92+52=106.
因为100<x2<121,
所以10<x<11,即x在整数10与11之间.
(2)因为10.12=102.01,10.22=104.04,10.32=106.09,
所以10.22<106<10.32.
因为106-104.04=1.96,106.09-106=0.09,
0.09<1.96,所以当x精确到0.1时,x≈10.3.
又因为10.292=105.884 1,10.302=106.09,所以10.292<106<10.302.
因为106-105.884 1=0.115 9,0.09<0.115 9,
所以当x精确到0.01时,x≈10.30.
[学习目标]
1.通过拼图活动,感受无理数产生的实际背景和引入的必要性.
2.借助计算器探索无理数是无限不循环小数并从中体会无限逼近的思想.
3.会判断一个数是有理数还是无理数.
[复习回顾]
1. 一个整数的平方一定是整数吗?
2. 一个分数的平方一定是分数吗?
[新知探究]
[任务一 探究不是有理数的数]
活动1:让学生用准备好的两个边长为1的正方形纸片,剪一剪,拼一拼,设法得到一个小的正方形。
学生可能出现的拼图结果:
问题1:(1)设大正方形的边长为a, a满足什么条件?
问题2:a可能是整数吗?说说你的理由。
问题3:a可能是分数吗?说说你的理由。
结论:a既不是整数,也不是分数,所以a不是有理数。
例1如图:(1)以直角三角形的斜边为边的正方形的面积是多少?(小正方形边长为1,中正方形边长为2)
(2)设该正方形的边长为b,b满足什么条件?
(3)b是有理数吗?
[即时测评]
1.如图,等边三角形的边长为2,高为h,h可能是整数吗?可能是分数吗?是有理数吗?
[任务二 探究无理数的概念]
活动2:面积为2的正方形的边长a究竟是多少呢?
问题1:如图,3个正方形的边长之间有怎样的大小关系?说说你的理由.
问题2:边长a的整数部分是几?十分位是几?百分位呢?千分位呢?.....借助计算器进行探究.
问题3:小明将他的探究过程整理如下:
思考?还可以继续算下去吗 a可能是有限小数吗
问题4:估计面积为5的正方形的边长b的值是多少?b可能是有限小数吗?与同学进行交流.
归纳总结:a是介于1和2之间的一个数,b是介于2和3之间的一个数,既不是整数,也不是分数,则a,b一定不是有理数.如果写成小数形式,是无限不循环小数.
活动3:把下列各数表示成小数,你发现了什么?
教师:有理数总可以用有限小数或无限循环小数表示.反过来,任何有限小数或无限循环小数也都是有理数.
教师:无限不循环小数称为无理数.
例2下列各数中,哪些是有理数 哪些是无理数
3.14,﹣,0.,0.101 000 100 000 1…(相邻两个1之间0的个数逐次加2).
[即时测评]
1.在下列数:﹣2.5,,0,﹣1.121121112…,,﹣π中,无理数有( )
A.1个 B.2个 C.3个 D.4个
2.在数﹣65,,3.14,0,,﹣π,0.020020002…中,无理数共有 个.
3.如图,△ABC中,∠C=90°,BC=4,AC=3,点P在线段AC上,若BP的长度是个无理数,则BP的长度可以是 .(写出一个即可)
[当堂达标]
1.的大小在两个相邻整数之间,这两个整数是( )
A.1和2 B.2和3 C.3和4 D.4和5
2.下列实数是无理数的是( )
A.﹣2025 B.π C.3.14159 D.
3以下各正方形的边长是无理数的是( )
A.面积为25的正方形;
B.面积为的正方形;
C.面积为8的正方形;
D.面积为1.44的正方形.
4.下列各数中:12,,,﹣|﹣1|,0.1010010001…(每两个1之间的0依次加1),其中,无理数有 个.
5.已知直角三角形的两直角边长分别是9 cm和5 cm,斜边长是x cm.
(1)估计x在哪两个连续整数之间;
(2)如果把x的结果精确到0.1,估计x的值;如果精确到 0.01 呢?
答案:
[任务一 探究不是有理数的数]
活动1:
问题1:因为 S大正方形 = 2,所以 = 2.
问题2:(1)如图:因为 = 2,而 = 1, = 4,
所以 < < .
所以 1< a < 2,故 a 不是整数.
(2)如图:在△ABC中,AC=1,AC=1,BC=a
根据三角形的三边关系: AB-AC< a
=>2,所以,不可能是分母为2的分数,其它的依次类推......
结论:a既不是整数,也不是分数,所以a不是有理数。
例1
解:(1)以直角三角形的斜边为边的正方形的面积为+=5;
(2)根据三角形的三边关系可得:1<b<3;
(3)b不是有理数.
[即时测评]
1.解:因为三角形是等边三角形,且AD⊥BC,
所以BD=DC,则BD=AB=1,
根据勾股定理得:
h不可能是整数;h也不可能是分数,也不是有理数.
[任务二 探究无理数的概念]
活动2:
问题1:1<a<2
问题2:边长a的整数部分是1,十分位是4,百分位是1,千分位是4.
问题3:a=1.414 213 56…, 它不可能是一个有限小数.
问题4:b=2.236067977···,不可能是有限小数.
归纳总结:a是介于1和2之间的一个数,b是介于2和3之间的一个数,既不是整数,也不是分数,则a,b一定不是有理数.如果写成小数形式,是无限不循环小数.
活动3:
例2
解:有理数有:3.14,﹣,0.;
无理数有:0.101 000 100 000 1…(相邻两个1之间0的个数逐次加2).
[即时测评]
1.B
2.2
3.(答案不唯一)
[当堂达标]
1.C
2.B
3.C
4.2
5.解:(1)根据题意,可得x2=92+52=106.
因为100<x2<121,
所以10<x<11,即x在整数10与11之间.
(2)因为10.12=102.01,10.22=104.04,10.32=106.09,
所以10.22<106<10.32.
因为106-104.04=1.96,106.09-106=0.09,
0.09<1.96,所以当x精确到0.1时,x≈10.3.
又因为10.292=105.884 1,10.302=106.09,所以10.292<106<10.302.
因为106-105.884 1=0.115 9,0.09<0.115 9,
所以当x精确到0.01时,x≈10.30.
