4.4 实数 第1课时 实数及其性质 导学案 (含答案) 2025-2026学年数学鲁教版(五四制)七年级上册
文档属性
| 名称 | 4.4 实数 第1课时 实数及其性质 导学案 (含答案) 2025-2026学年数学鲁教版(五四制)七年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 320.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-19 13:38:07 | ||
图片预览




文档简介
4 实数
第1课时 实数及其性质
[学习目标]
1.了解实数的意义,能对实数按要求进行分类.
2.了解实数范围内,相反数、倒数、绝对值的意义.
3.了解数轴上的点与实数一一对应,能用数轴上的点来表示无理数.
[新知探究]
[任务一 探究实数的概念及分类]
活动1 按要求完成下列各题.
把下列各数分别填入相应的集合内:
,,,π,-,,,-,-,,0,0.373 773 777 3……(相邻两个3之间7的个数逐次增加1)
教师:有理数和无理数统称为实数.
问题1:从实数的概念考虑,实数如何分类?
总结:实数
问题2:无理数和有理数一样,也有正负之分.从符号考虑,你能把上面的数填入相应的集合内吗?
思考:0属于正数吗?0属于负数吗?
问题3:从实数的符号考虑,实数如何分类?
总结:实数
例1将下列各数填入相应的集合中:
﹣7,0,﹣22,﹣2.55555……,3.01,+9,4.020020002…,+10%,﹣2π
有理数集合:{ ……};
无理数集合:{ ……};
整数集合:{ ……};
分数集合:{ ……}.
[即时测评]
1.在实数,0,﹣0.3,3.1415926,4,﹣2022,π中,有理数的个数为( )
A.3 B.4 C.5 D.6
2.下列各数中,是负数的是( )
A. B.0 C.0.2 D.
3.已知下列实数:
①0,②,③,④,⑤3.2,⑥.(只需填写序号)
其中整数有: ,分数有: ,无理数有: .
4.把下列各数的序号填在相应的大括号中:
①﹣9;②3.5;③:④,⑤;⑥0.1010010001…(两个1之间的0逐次增加);⑦.
(1)整数集合:{ …};
(2)分数集合:{ …};
(3)有理数集合:{ …};
(4)无理数集合:{ …}.
[任务二 探究实数的性质及运算]
活动2:思考回答下列问题.
问题1:在有理数中,数a的相反数是什么 绝对值是什么 当a不为0时,它的倒数是什么?
问题2:的相反数是什么 的倒数是什么 ,0,-π的绝对值分别是什么
问题3:3-π的绝对值是 .
问题4:a是一个实数,它的相反数是 ,它的绝对值是 ,当a≠0时,它的倒数是 .
总结:
(1)相反数:a与-a互为相反数;0的相反数仍是0;
(2)倒数:当a≠0时,a与互为倒数(0没有倒数);
(3)绝对值:正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0;
即|a|=
例2 说出下列各式计算的依据.
(1)
(2)
(3)
(4)(10)-10=(10-10)=0=
[即时测评]
1.下列各组数中,互为相反数的一组是( )
A.﹣3与 B.﹣3与
C.﹣3与 D.3与|﹣3|
2.的相反数是( )
A. B. C. D.
3.已知一个数的绝对值是,则这个数是( )
A. B. C.3 D.
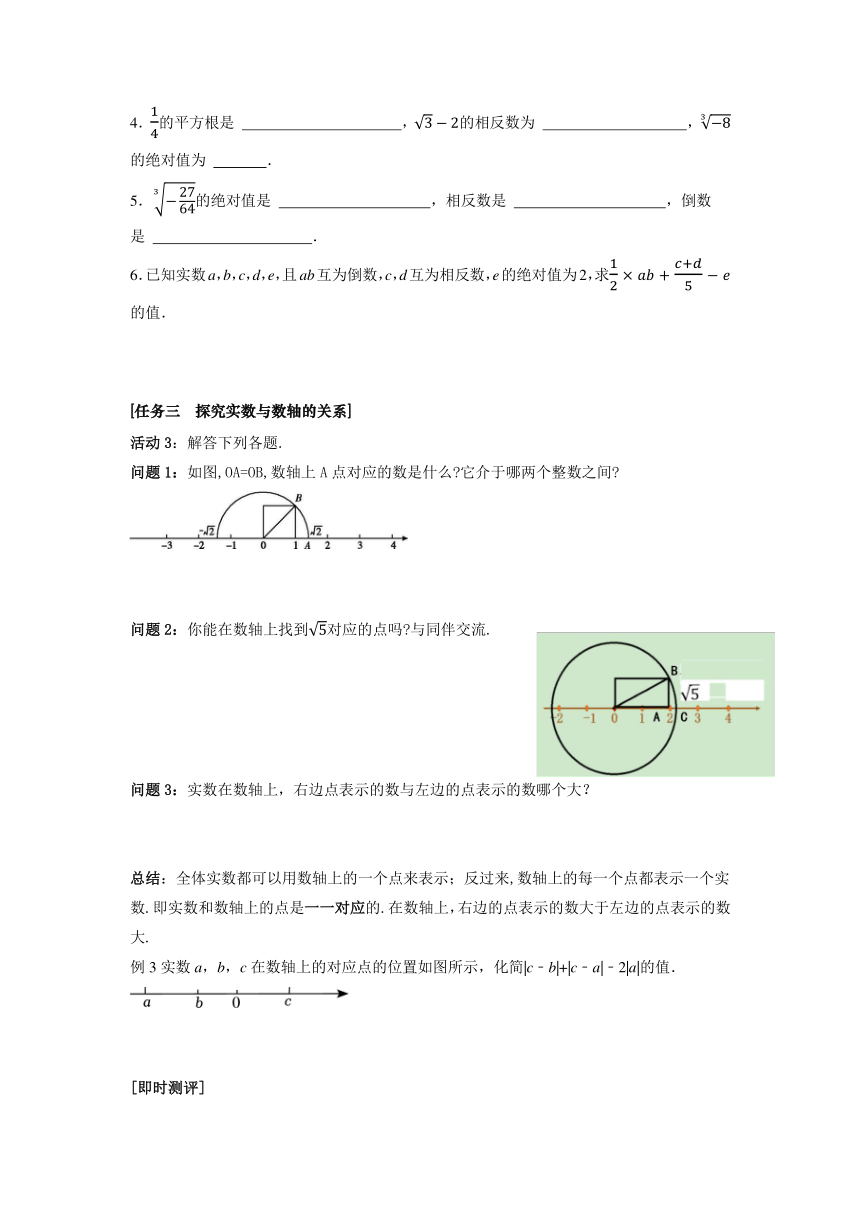
4.的平方根是 ,的相反数为 ,的绝对值为 .
5.的绝对值是 ,相反数是 ,倒数是 .
6.已知实数a,b,c,d,e,且ab互为倒数,c,d互为相反数,e的绝对值为2,求 的值.
[任务三 探究实数与数轴的关系]
活动3:解答下列各题.
问题1:如图,OA=OB,数轴上A点对应的数是什么 它介于哪两个整数之间
问题2:你能在数轴上找到对应的点吗 与同伴交流.
问题3:实数在数轴上,右边点表示的数与左边的点表示的数哪个大?
总结:全体实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.即实数和数轴上的点是一一对应的.在数轴上,右边的点表示的数大于左边的点表示的数大.
例3实数a,b,c在数轴上的对应点的位置如图所示,化简|c﹣b|+|c﹣a|﹣2|a|的值.
[即时测评]
1.如图,将实数表示在数轴上,对应的点可能是( )
A.R点 B.Q点 C.S点 D.T点
2.如图,正方形OBCD的面积为3,OA=OB,则数轴上点A对应的数是 .
3.A,B为数轴上两点,点A表示的数为1,点B到点A的距离是,则点B表示的数为 .
4.已知三个实数a、b、c在数轴上对应的点如图所示.
(1)判断正负:
a﹣b 0,c﹣a 0,c+b 0,a+b 0.
(2)根据(1)中的判断化简:|a﹣b|+|c﹣a|﹣|c+b|﹣|a+b|.
[当堂达标]
1.下列各数中,是无理数的是( )
A.-1.732 B. 1,414 C. D.3.14
2.已知一个数a的绝对值是,则( )
A. B. C.或 D.或
3.的相反数是 .的倒数是 ,||= .
4.如图,正方形ABCD的面积为7,顶点A与数轴上表示数1的点重合,点E在数轴上,且在点A的左侧,AD=AE,则点E表示的数是 .
5.把下列各数填在相应的括号内:
∣-∣;;;π;0.;﹣;;3;0.13。
有理数集合{ }
无理数集合{ }
整数集合 { }
分数集合{ }
实数集合{ }
6.实数a,b在数轴上对应点的位置如图所示,.
化简M。
答案:
[任务一 探究实数的概念及分类]
活动1 :
教师:有理数和无理数统称为实数.
问题1:从实数的概念考虑,实数如何分类?
总结:实数
问题2:无理数和有理数一样,也有正负之分.从符号考虑,你能把上面的数填入相应的集合内吗?
思考: 0既不是正数,也不是负数
问题3:从实数的符号考虑,实数如何分类?
总结:实数
例1解:在﹣7,0,﹣22,﹣2.55555……,3.01,+9,4.020020002…,+10%,﹣2π中,
有理数有:﹣7,0,﹣22,﹣2.55555……,3.01,+9,+10%;
无理数有:4.020020002…,﹣2π;
整数有:﹣7,0,+9;
分数有:﹣22,﹣2.55555……,3.01,+10%.
[即时测评]
1.D
2.A
3.其中整数有: ①③ ,分数有: ⑤⑥ ,无理数有: ②④ .
4.解:(1)整数集合:{①⑦};
(2)分数集合:{②};
(3)有理数集合:{①②⑦};
(4)故无理数集合{③④⑤⑥}.
[任务二 探究实数的性质及运算]
活动2:
问题1:数a的相反数是-a,绝对值是∣a∣,当a不为0时,它的倒数是。
问题2:的相反数是-的倒数是;,0,-π的绝对值分别是,0,π。
问题3:π-3。
问题4:-a,∣a∣,。
总结:
(1)相反数:a与-a互为相反数;0的相反数仍是0;
(2)倒数:当a≠0时,a与互为倒数(0没有倒数);
(3)绝对值:正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0;
即|a|=
例2
解:(1)乘法交换律
(2)乘法结合律
(3)合并同类根式
(4)去括号及加法结合律
[即时测评]
1.A
2.A
3.D
4.,,2.
5.,,.
6.解:由题意可得:ab=1,c+d=0,e=±2,
(1)原式122;
(2)原式122,
综上所述:原式的值为或.
[任务三 探究实数与数轴的关系]
活动3:解答下列各题.
问题1:根据勾股定理,OB==,因为OA=OB,所以OA=,它介于1和2两个整数之间.
问题2:(1)如图,在数轴上取OA=2;
(2)过点A作 AB⊥OA且AB=1;
(3)根据勾股定理,得
OB== = ;
(4) 以点O为圆心,以OB为半径画弧,交x轴与点C,
则点C对应的点是 。
问题3:实数在数轴上,右边点表示的数比左边的点表示的数大。
例3解:由数轴得c﹣b>0,c﹣a>0,a<0,
原式=c﹣b+c﹣a+2a=2c﹣b+a.
[即时测评]
1.D
2.
3.1或1.
4.解:(1)<,>,>,<;
(2)|a﹣b|+|c﹣a|﹣|c+b|﹣|a+b|
=﹣(a﹣b)+(c﹣a)﹣(c+b)﹣[﹣(a+b)]
=﹣a+b+c﹣a﹣c﹣b+a+b
=﹣a+b.
[当堂达标]
1.C
2.C
3.,,2
4.
5.有理数集合{∣-∣;;0.;﹣;3;0.13...... }
无理数集合{ ;π;;...... }
整数集合 { ∣-∣;;3;...... }
分数集合{ ﹣;...... }
实数集合{ ∣-∣;;;π;0.;﹣;;3;0.13...... }
6解:由数轴可得:b<﹣2,0<a<2,
∴a+2>0,b﹣2<0,a﹣b>0,
∴
=a+2﹣[﹣(b﹣2)]+a﹣b+(﹣b)
=a+2+b﹣2+a﹣b﹣b
=2a﹣b。
第1课时 实数及其性质
[学习目标]
1.了解实数的意义,能对实数按要求进行分类.
2.了解实数范围内,相反数、倒数、绝对值的意义.
3.了解数轴上的点与实数一一对应,能用数轴上的点来表示无理数.
[新知探究]
[任务一 探究实数的概念及分类]
活动1 按要求完成下列各题.
把下列各数分别填入相应的集合内:
,,,π,-,,,-,-,,0,0.373 773 777 3……(相邻两个3之间7的个数逐次增加1)
教师:有理数和无理数统称为实数.
问题1:从实数的概念考虑,实数如何分类?
总结:实数
问题2:无理数和有理数一样,也有正负之分.从符号考虑,你能把上面的数填入相应的集合内吗?
思考:0属于正数吗?0属于负数吗?
问题3:从实数的符号考虑,实数如何分类?
总结:实数
例1将下列各数填入相应的集合中:
﹣7,0,﹣22,﹣2.55555……,3.01,+9,4.020020002…,+10%,﹣2π
有理数集合:{ ……};
无理数集合:{ ……};
整数集合:{ ……};
分数集合:{ ……}.
[即时测评]
1.在实数,0,﹣0.3,3.1415926,4,﹣2022,π中,有理数的个数为( )
A.3 B.4 C.5 D.6
2.下列各数中,是负数的是( )
A. B.0 C.0.2 D.
3.已知下列实数:
①0,②,③,④,⑤3.2,⑥.(只需填写序号)
其中整数有: ,分数有: ,无理数有: .
4.把下列各数的序号填在相应的大括号中:
①﹣9;②3.5;③:④,⑤;⑥0.1010010001…(两个1之间的0逐次增加);⑦.
(1)整数集合:{ …};
(2)分数集合:{ …};
(3)有理数集合:{ …};
(4)无理数集合:{ …}.
[任务二 探究实数的性质及运算]
活动2:思考回答下列问题.
问题1:在有理数中,数a的相反数是什么 绝对值是什么 当a不为0时,它的倒数是什么?
问题2:的相反数是什么 的倒数是什么 ,0,-π的绝对值分别是什么
问题3:3-π的绝对值是 .
问题4:a是一个实数,它的相反数是 ,它的绝对值是 ,当a≠0时,它的倒数是 .
总结:
(1)相反数:a与-a互为相反数;0的相反数仍是0;
(2)倒数:当a≠0时,a与互为倒数(0没有倒数);
(3)绝对值:正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0;
即|a|=
例2 说出下列各式计算的依据.
(1)
(2)
(3)
(4)(10)-10=(10-10)=0=
[即时测评]
1.下列各组数中,互为相反数的一组是( )
A.﹣3与 B.﹣3与
C.﹣3与 D.3与|﹣3|
2.的相反数是( )
A. B. C. D.
3.已知一个数的绝对值是,则这个数是( )
A. B. C.3 D.
4.的平方根是 ,的相反数为 ,的绝对值为 .
5.的绝对值是 ,相反数是 ,倒数是 .
6.已知实数a,b,c,d,e,且ab互为倒数,c,d互为相反数,e的绝对值为2,求 的值.
[任务三 探究实数与数轴的关系]
活动3:解答下列各题.
问题1:如图,OA=OB,数轴上A点对应的数是什么 它介于哪两个整数之间
问题2:你能在数轴上找到对应的点吗 与同伴交流.
问题3:实数在数轴上,右边点表示的数与左边的点表示的数哪个大?
总结:全体实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.即实数和数轴上的点是一一对应的.在数轴上,右边的点表示的数大于左边的点表示的数大.
例3实数a,b,c在数轴上的对应点的位置如图所示,化简|c﹣b|+|c﹣a|﹣2|a|的值.
[即时测评]
1.如图,将实数表示在数轴上,对应的点可能是( )
A.R点 B.Q点 C.S点 D.T点
2.如图,正方形OBCD的面积为3,OA=OB,则数轴上点A对应的数是 .
3.A,B为数轴上两点,点A表示的数为1,点B到点A的距离是,则点B表示的数为 .
4.已知三个实数a、b、c在数轴上对应的点如图所示.
(1)判断正负:
a﹣b 0,c﹣a 0,c+b 0,a+b 0.
(2)根据(1)中的判断化简:|a﹣b|+|c﹣a|﹣|c+b|﹣|a+b|.
[当堂达标]
1.下列各数中,是无理数的是( )
A.-1.732 B. 1,414 C. D.3.14
2.已知一个数a的绝对值是,则( )
A. B. C.或 D.或
3.的相反数是 .的倒数是 ,||= .
4.如图,正方形ABCD的面积为7,顶点A与数轴上表示数1的点重合,点E在数轴上,且在点A的左侧,AD=AE,则点E表示的数是 .
5.把下列各数填在相应的括号内:
∣-∣;;;π;0.;﹣;;3;0.13。
有理数集合{ }
无理数集合{ }
整数集合 { }
分数集合{ }
实数集合{ }
6.实数a,b在数轴上对应点的位置如图所示,.
化简M。
答案:
[任务一 探究实数的概念及分类]
活动1 :
教师:有理数和无理数统称为实数.
问题1:从实数的概念考虑,实数如何分类?
总结:实数
问题2:无理数和有理数一样,也有正负之分.从符号考虑,你能把上面的数填入相应的集合内吗?
思考: 0既不是正数,也不是负数
问题3:从实数的符号考虑,实数如何分类?
总结:实数
例1解:在﹣7,0,﹣22,﹣2.55555……,3.01,+9,4.020020002…,+10%,﹣2π中,
有理数有:﹣7,0,﹣22,﹣2.55555……,3.01,+9,+10%;
无理数有:4.020020002…,﹣2π;
整数有:﹣7,0,+9;
分数有:﹣22,﹣2.55555……,3.01,+10%.
[即时测评]
1.D
2.A
3.其中整数有: ①③ ,分数有: ⑤⑥ ,无理数有: ②④ .
4.解:(1)整数集合:{①⑦};
(2)分数集合:{②};
(3)有理数集合:{①②⑦};
(4)故无理数集合{③④⑤⑥}.
[任务二 探究实数的性质及运算]
活动2:
问题1:数a的相反数是-a,绝对值是∣a∣,当a不为0时,它的倒数是。
问题2:的相反数是-的倒数是;,0,-π的绝对值分别是,0,π。
问题3:π-3。
问题4:-a,∣a∣,。
总结:
(1)相反数:a与-a互为相反数;0的相反数仍是0;
(2)倒数:当a≠0时,a与互为倒数(0没有倒数);
(3)绝对值:正数的绝对值是它本身;负数的绝对值是它的相反数;0的绝对值是0;
即|a|=
例2
解:(1)乘法交换律
(2)乘法结合律
(3)合并同类根式
(4)去括号及加法结合律
[即时测评]
1.A
2.A
3.D
4.,,2.
5.,,.
6.解:由题意可得:ab=1,c+d=0,e=±2,
(1)原式122;
(2)原式122,
综上所述:原式的值为或.
[任务三 探究实数与数轴的关系]
活动3:解答下列各题.
问题1:根据勾股定理,OB==,因为OA=OB,所以OA=,它介于1和2两个整数之间.
问题2:(1)如图,在数轴上取OA=2;
(2)过点A作 AB⊥OA且AB=1;
(3)根据勾股定理,得
OB== = ;
(4) 以点O为圆心,以OB为半径画弧,交x轴与点C,
则点C对应的点是 。
问题3:实数在数轴上,右边点表示的数比左边的点表示的数大。
例3解:由数轴得c﹣b>0,c﹣a>0,a<0,
原式=c﹣b+c﹣a+2a=2c﹣b+a.
[即时测评]
1.D
2.
3.1或1.
4.解:(1)<,>,>,<;
(2)|a﹣b|+|c﹣a|﹣|c+b|﹣|a+b|
=﹣(a﹣b)+(c﹣a)﹣(c+b)﹣[﹣(a+b)]
=﹣a+b+c﹣a﹣c﹣b+a+b
=﹣a+b.
[当堂达标]
1.C
2.C
3.,,2
4.
5.有理数集合{∣-∣;;0.;﹣;3;0.13...... }
无理数集合{ ;π;;...... }
整数集合 { ∣-∣;;3;...... }
分数集合{ ﹣;...... }
实数集合{ ∣-∣;;;π;0.;﹣;;3;0.13...... }
6解:由数轴可得:b<﹣2,0<a<2,
∴a+2>0,b﹣2<0,a﹣b>0,
∴
=a+2﹣[﹣(b﹣2)]+a﹣b+(﹣b)
=a+2+b﹣2+a﹣b﹣b
=2a﹣b。
