人教A版高中数学必修第一册第二章一元二次函数、方程和不等式2.1等式性质与不等式性质(第1课时)课件(共62张PPT)
文档属性
| 名称 | 人教A版高中数学必修第一册第二章一元二次函数、方程和不等式2.1等式性质与不等式性质(第1课时)课件(共62张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 09:20:22 | ||
图片预览







文档简介
(共62张PPT)
人教版2019高一数学(必修一)第一章 一元二次函数、方程和不等式
第一课时 等式性质与不等式性质
2.1 等式性质与不等式性质
学习目标
了解不等式的意义,能用不等式(组)表示实际问题
中的不等关系.
2. 会用作差法比较两个代数式的大小关系.(重点)
3. 掌握并会应用重要不等式.(重难点)
情景导入
在现实世界和日常生活中,大量存在着相等关系和不等关系,
例如多与少、大与小、长与短、高与矮、远与近、快与慢、涨与跌,轻与重,不超过或不少于等.
类似于这样的问题,反映在数量关系上,就是相等与不等.
相等用等式表示,不等用不等式表示.
【等式】指的是用等号“=”连接起来的式子
【不等式】指的是用不等号
“≠”“>”“<”“≥”“≤”
连接起来的式子
1.不等关系与不等式
新知探究
【问题1】你能用不等式或不等式组表示下列问题中的不等关系吗?
(3)三角形两边之和大于第三边,两边之差小于第三边;
(4)连接直线外一点与直线上各点的所有线段中,垂线段最短.
设P是直线AB外任意一点,PQ是P到AB的垂
线段,C是直线AB上任意一点,则PC≥PQ
A
B
C
P
Q
以上我们根据实际问题所蕴含的不等关系抽象出了不等式.
接着,就可以用不等式研究相应的问题了.
【问题2】某种杂志原以每本2.5元的价格销售,可以售出8万本.根据市场调查,若单价每提高0.1元,销售量就可能相应减少2 000本,若把提价后杂志的定价设为x元,怎样用不等式表示销售的总收入仍不低于20万元?
我们该如何解这个不等式呢?
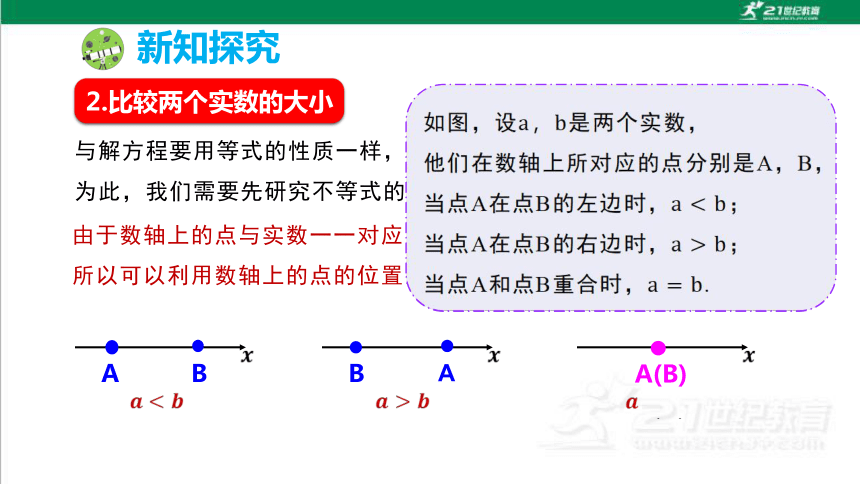
由于数轴上的点与实数一一对应,
所以可以利用数轴上的点的位置关系来规定实数的大小关系;
2.比较两个实数的大小
新知探究
与解方程要用等式的性质一样,解不等式要用不等式的性质.
为此,我们需要先研究不等式的性质.
A
B
B
A
A(B)
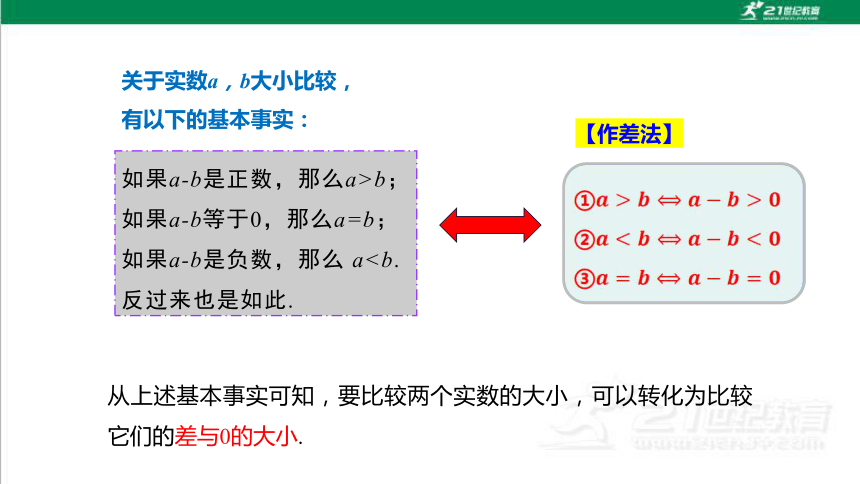
关于实数a,b大小比较,
有以下的基本事实:
如果a-b是正数,那么a>b;
如果a-b等于0,那么a=b;
如果a-b是负数,那么 a反过来也是如此.
从上述基本事实可知,要比较两个实数的大小,可以转化为比较它们的差与0的大小.
【解】运用作差法:
作差
变形
定号
定论
0是相等与不等的分界线,它也为比较实数的大小提供了标杆.
这里,我们借助多项式减法运算,得出了一个明显大于0的数(式).
这是解决不等式问题的常用方法.
课本例题
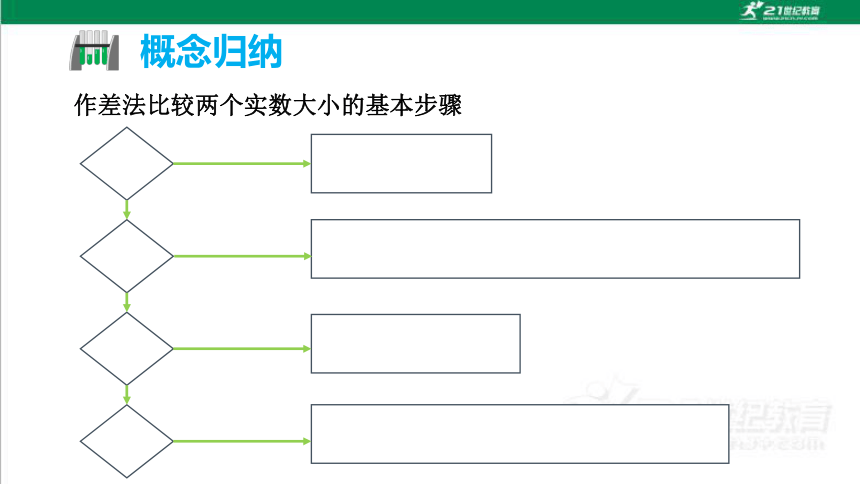
作差法比较两个实数大小的基本步骤
概念归纳
作差
变形
定号
结论
a-b
采用配方、因式分解、通分、有理化等手段
判断差与0的大小
利用实数a,b大小比较的基本事实
下图是在北京召开的第24届国际数学家大会的会标,会标是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去像一个风车,代表中国人民热情好客.你能在这个图中找出一些相等关系和不等关系吗?
思考探究
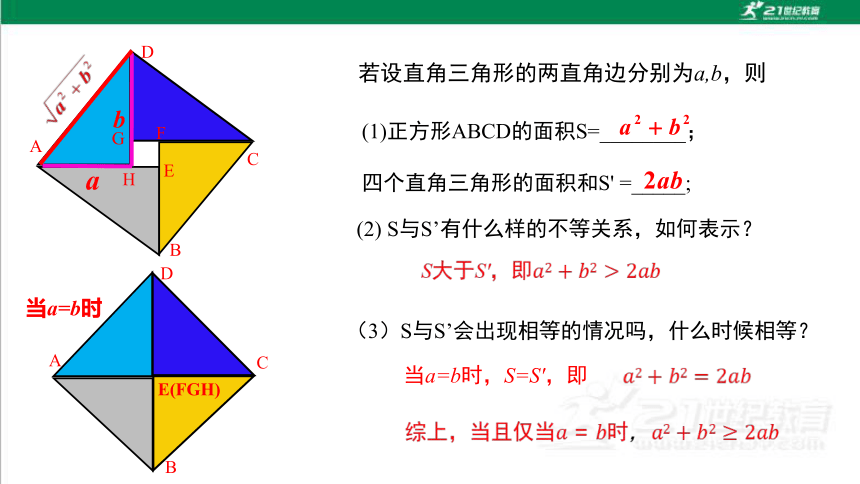
(1)正方形ABCD的面积S=________;
四个直角三角形的面积和S' =_____;
(2) S与S’有什么样的不等关系,如何表示?
(3)S与S’会出现相等的情况吗,什么时候相等?
若设直角三角形的两直角边分别为a,b,则
A
B
C
D
E(FGH)
当a=b时,S=S',即
A
B
C
D
E
F
G
H
a
b
当a=b时
如何证明不等式成立?
证明:
提示:利用完全平方公式即可
例1.用一段长为30 m的篱笆围成一个一边靠墙的矩形菜园,墙长18 m,要求菜园的面积不小于110 m2,靠墙的一边长为x m.
试用不等式表示其中的不等关系.
探究一 用不等式(组)表示不等式关系
典例剖析
不等式(组)表示实际问题中不等关系的步骤
(1)审题.通读题目,分清楚已知量和待求量,设出待求量;
(2)列不等关系.列出待求量具备哪些不等关系(即满足什么条件);
(3)列不等式(组).挖掘题意,建立已知量和待求量之间的关系式,并分析某些变量的约束条件(包含隐含条件).
概念归纳
1.某钢铁厂要把长度为4 000 mm的钢管截成500 mm和600 mm两种,按照生产的要求,600 mm钢管的数量不能超过500 mm钢管的3倍,试写出满足上述所有不等关系的不等式.
练一练
例2.已知x∈R,比较x3-1与2x2-2x的大小.
探究二 比较大小问题
典例剖析
比较两个代数式大小的步骤
(1)作差:对要比较大小的两个数(或式子)作差;
(2)变形:对差进行变形;
(3)定号:结合变形的结果及题设条件判断差的符号;
(4)结论.
提醒:这种比较大小的方法通常称为作差比较法.其思维过程:作差→变形→判断符号→结论,其中变形是判断符号的前提.
概念归纳
2.若y1=3x2-x+1,y2=2x2+x-1,则y1与y2的大小关系是( )
A.y1>y2 B.y1=y2
C.y1练一练
解析:
∵ y1-y2=x2-2x+2=(x-1)2+1>0,
∴ y1>y2.
A
练一练
1.下面能表示“m与n的和是非正数”的不等式为( )
A.m+n<0 B.m+n>0 C.m+n≤0 D.m+n≥0
随堂练
2.设M=x2,N=-x-1,则M与N的大小关系是( )
A.M>N B.M=N
C.MC
A
随堂练
4.一单位的甲、乙、丙三人出差A城办事;在安排住宿时,他们有三种住宿方案可供选择:
(1)三人同住一套间;
(2)二人住标准间(双人间)、一人住单间;
(3)三人各住一个单间.若宾馆方面对每个套间、每个标准间及单间的标价分别为300元、160元和60元;
同时对客户实行打折优惠,但这三类房间的折率各不相同,
分别为50%,65%和85%,
这三人选择住宿方案中最经济的为第 套方案.
随堂练
(1)
解析:
若选择(1)方案,则需支付:y1=300×50%=150(元);
若选择(2)方案,则需支付:y2=160×65%+60×85%=155(元);
若选择(3)方案,则需支付:y3=60×85%×3=153(元).
因为y1随堂练
5.分别写出满足下列条件的不等关系:
(1)一个两位数的个位数字y比十位数字x大,且这个两位数小于30;
(2)某电脑用户计划用不超过500元的资金购买单价分别为60元的单片软件x片和70元的盒装磁盘y盒.根据需要,软件至少买3片,磁盘至少买2盒.
解:(1)y>x>0,9<10x+y<30,且x,y∈N*.
(2)x≥3,y≥2,60x+70y≤500,且x,y∈N*.
随堂练
解 0(2)a与b的和是非负实数;
解 a+b≥0;
(1)某高速公路规定通过车辆的车货总高度h(单位:m)
从地面算起不能超过4 m;
1.用不等式或不等式组表示下面的不等关系.
课本练习
(3)如图,在一个面积小于350m2的矩形地基中心位置上建造一个仓库,仓库的四周建成绿地,仓库的长L(单位:m)大于宽W(单位:m)的4倍.
课本练习
2.比较(x+3)(x+7)和(x+4)(x+6)的大小.
解 因为(x+3)(x+7)-(x+4)(x+6)
=(x2+10x+21)-(x2+10x+24)
=-3<0,
所以(x+3)(x+7)<(x+4)(x+6).
课本练习
课本练习
错因分析
1.若a>b,则ac2________bc2.
易错警示 忽视因式可能为0
错解:因为c2>0,且a>b,所以ac2>bc2,故填>.
易错防范:上面的解法错在忽视了c=0的情况.当c=0时,ac2=bc2.防范措施是使用不等式的性质时,不可忽视条件.
正解:因为c2≥0,且a>b,所以ac2≥bc2,故应填≥.
2.若A=a2+3ab,B=4ab-b2,则A,B的大小关系是( )
A.A≤B B.A≥B
C.A>B D.大小关系不确定
错因分析
因忽视配方法在判断符号中的应用致错
错解:因为A-B=a2+3ab-4ab+b2=a2+b2-ab,所以A,B的大小关系不确定.
B
防范措施
1.用作差法比较两个数(式)的大小时,其关键是变形,一般采用配方、因式分解、通分、有理化等手段变形,这样有利于定号.特别是作差后的式子为二次三项式时,常考虑因式分解或配方法变形.
2.注意培养逻辑推理素养和数学运算素养.
归纳总结
分层练习-基础
D
分层练习-基础
D
分层练习-基础
A
分层练习-基础
A
分层练习-基础
D
分层练习-基础
A
分层练习-基础
C
分层练习-基础
分层练习-基础
<
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
A
分层练习-巩固
分层练习-巩固
B
分层练习-巩固
现实生活中的许多问题能够用不等式解决,其解题思路是将解决的问题转化成不等关系,利用作差法比较大小,进而解决实际问题.
分层练习-巩固
分层练习-拓展
分层练习-拓展
2.有一批衬衣原价为每件80元,甲、乙两商场均有销售.现在每个商场都推出了促销政策:到甲商场买一件衬衣优惠4元,买两件每件优惠8元,买三件每件优惠12元,……依此类推,直至减到半价为止;乙商场则一律按原价7折酬宾.某单位欲为每位员工购买一件该衬衣,问:到哪个商场购买比较合算?
解:设该单位共需购买x件衬衣,在甲、乙两商场购买分别需付款y元、z元.依题意,有
z=80×70%x=56x(x≥1,x∈Z).
分层练习-拓展
①若1≤x≤10,x∈Z,则y-z=(80-4x)x-56x=4x(6-x).
当1≤x≤5,x∈Z时,6-x>0,∴y-z>0,即y>z.
当x=6时,y-z=0,即y=z.
当7≤x≤10,x∈Z时,6-x<0,
∴y-z<0,即y<z.
②若x>10,x∈Z,则y-z=40x-56x=-16x.
∵-16x<0,∴y<z.
综上,若单位人数不超过5人,到乙商场购买合算;若单位人数恰为6人,到甲、乙商场购买一样合算;若单位人数超过6人,到甲商场购买更合算.
分层练习-拓展
分层练习-拓展
分层练习-拓展
不等关系与
比较大小
利用不等式表示不等关系
比较大小
作差法:通常利用配方法化成完全平方式与0比较
作商法:适用于同号的式子作商与1比较
比较大小常用方法
(1)利用不等式时,要注意等号能否取到
(2)利用不等式表示不等关系时要注意实际意义
数学建模:用不等式(组)表示实际问题,培养数学建模的核心素养
逻辑推理:通过等式性质类比推理得不等式的性质,培养逻辑推理的核心素养
方法总结
核心知识
易错提醒
核心素养
课堂小结
人教版2019高一数学(必修一)第一章 一元二次函数、方程和不等式
第一课时 等式性质与不等式性质
2.1 等式性质与不等式性质
学习目标
了解不等式的意义,能用不等式(组)表示实际问题
中的不等关系.
2. 会用作差法比较两个代数式的大小关系.(重点)
3. 掌握并会应用重要不等式.(重难点)
情景导入
在现实世界和日常生活中,大量存在着相等关系和不等关系,
例如多与少、大与小、长与短、高与矮、远与近、快与慢、涨与跌,轻与重,不超过或不少于等.
类似于这样的问题,反映在数量关系上,就是相等与不等.
相等用等式表示,不等用不等式表示.
【等式】指的是用等号“=”连接起来的式子
【不等式】指的是用不等号
“≠”“>”“<”“≥”“≤”
连接起来的式子
1.不等关系与不等式
新知探究
【问题1】你能用不等式或不等式组表示下列问题中的不等关系吗?
(3)三角形两边之和大于第三边,两边之差小于第三边;
(4)连接直线外一点与直线上各点的所有线段中,垂线段最短.
设P是直线AB外任意一点,PQ是P到AB的垂
线段,C是直线AB上任意一点,则PC≥PQ
A
B
C
P
Q
以上我们根据实际问题所蕴含的不等关系抽象出了不等式.
接着,就可以用不等式研究相应的问题了.
【问题2】某种杂志原以每本2.5元的价格销售,可以售出8万本.根据市场调查,若单价每提高0.1元,销售量就可能相应减少2 000本,若把提价后杂志的定价设为x元,怎样用不等式表示销售的总收入仍不低于20万元?
我们该如何解这个不等式呢?
由于数轴上的点与实数一一对应,
所以可以利用数轴上的点的位置关系来规定实数的大小关系;
2.比较两个实数的大小
新知探究
与解方程要用等式的性质一样,解不等式要用不等式的性质.
为此,我们需要先研究不等式的性质.
A
B
B
A
A(B)
关于实数a,b大小比较,
有以下的基本事实:
如果a-b是正数,那么a>b;
如果a-b等于0,那么a=b;
如果a-b是负数,那么 a
从上述基本事实可知,要比较两个实数的大小,可以转化为比较它们的差与0的大小.
【解】运用作差法:
作差
变形
定号
定论
0是相等与不等的分界线,它也为比较实数的大小提供了标杆.
这里,我们借助多项式减法运算,得出了一个明显大于0的数(式).
这是解决不等式问题的常用方法.
课本例题
作差法比较两个实数大小的基本步骤
概念归纳
作差
变形
定号
结论
a-b
采用配方、因式分解、通分、有理化等手段
判断差与0的大小
利用实数a,b大小比较的基本事实
下图是在北京召开的第24届国际数学家大会的会标,会标是根据中国古代数学家赵爽的弦图设计的,颜色的明暗使它看上去像一个风车,代表中国人民热情好客.你能在这个图中找出一些相等关系和不等关系吗?
思考探究
(1)正方形ABCD的面积S=________;
四个直角三角形的面积和S' =_____;
(2) S与S’有什么样的不等关系,如何表示?
(3)S与S’会出现相等的情况吗,什么时候相等?
若设直角三角形的两直角边分别为a,b,则
A
B
C
D
E(FGH)
当a=b时,S=S',即
A
B
C
D
E
F
G
H
a
b
当a=b时
如何证明不等式成立?
证明:
提示:利用完全平方公式即可
例1.用一段长为30 m的篱笆围成一个一边靠墙的矩形菜园,墙长18 m,要求菜园的面积不小于110 m2,靠墙的一边长为x m.
试用不等式表示其中的不等关系.
探究一 用不等式(组)表示不等式关系
典例剖析
不等式(组)表示实际问题中不等关系的步骤
(1)审题.通读题目,分清楚已知量和待求量,设出待求量;
(2)列不等关系.列出待求量具备哪些不等关系(即满足什么条件);
(3)列不等式(组).挖掘题意,建立已知量和待求量之间的关系式,并分析某些变量的约束条件(包含隐含条件).
概念归纳
1.某钢铁厂要把长度为4 000 mm的钢管截成500 mm和600 mm两种,按照生产的要求,600 mm钢管的数量不能超过500 mm钢管的3倍,试写出满足上述所有不等关系的不等式.
练一练
例2.已知x∈R,比较x3-1与2x2-2x的大小.
探究二 比较大小问题
典例剖析
比较两个代数式大小的步骤
(1)作差:对要比较大小的两个数(或式子)作差;
(2)变形:对差进行变形;
(3)定号:结合变形的结果及题设条件判断差的符号;
(4)结论.
提醒:这种比较大小的方法通常称为作差比较法.其思维过程:作差→变形→判断符号→结论,其中变形是判断符号的前提.
概念归纳
2.若y1=3x2-x+1,y2=2x2+x-1,则y1与y2的大小关系是( )
A.y1>y2 B.y1=y2
C.y1
解析:
∵ y1-y2=x2-2x+2=(x-1)2+1>0,
∴ y1>y2.
A
练一练
1.下面能表示“m与n的和是非正数”的不等式为( )
A.m+n<0 B.m+n>0 C.m+n≤0 D.m+n≥0
随堂练
2.设M=x2,N=-x-1,则M与N的大小关系是( )
A.M>N B.M=N
C.M
A
随堂练
4.一单位的甲、乙、丙三人出差A城办事;在安排住宿时,他们有三种住宿方案可供选择:
(1)三人同住一套间;
(2)二人住标准间(双人间)、一人住单间;
(3)三人各住一个单间.若宾馆方面对每个套间、每个标准间及单间的标价分别为300元、160元和60元;
同时对客户实行打折优惠,但这三类房间的折率各不相同,
分别为50%,65%和85%,
这三人选择住宿方案中最经济的为第 套方案.
随堂练
(1)
解析:
若选择(1)方案,则需支付:y1=300×50%=150(元);
若选择(2)方案,则需支付:y2=160×65%+60×85%=155(元);
若选择(3)方案,则需支付:y3=60×85%×3=153(元).
因为y1
5.分别写出满足下列条件的不等关系:
(1)一个两位数的个位数字y比十位数字x大,且这个两位数小于30;
(2)某电脑用户计划用不超过500元的资金购买单价分别为60元的单片软件x片和70元的盒装磁盘y盒.根据需要,软件至少买3片,磁盘至少买2盒.
解:(1)y>x>0,9<10x+y<30,且x,y∈N*.
(2)x≥3,y≥2,60x+70y≤500,且x,y∈N*.
随堂练
解 0
解 a+b≥0;
(1)某高速公路规定通过车辆的车货总高度h(单位:m)
从地面算起不能超过4 m;
1.用不等式或不等式组表示下面的不等关系.
课本练习
(3)如图,在一个面积小于350m2的矩形地基中心位置上建造一个仓库,仓库的四周建成绿地,仓库的长L(单位:m)大于宽W(单位:m)的4倍.
课本练习
2.比较(x+3)(x+7)和(x+4)(x+6)的大小.
解 因为(x+3)(x+7)-(x+4)(x+6)
=(x2+10x+21)-(x2+10x+24)
=-3<0,
所以(x+3)(x+7)<(x+4)(x+6).
课本练习
课本练习
错因分析
1.若a>b,则ac2________bc2.
易错警示 忽视因式可能为0
错解:因为c2>0,且a>b,所以ac2>bc2,故填>.
易错防范:上面的解法错在忽视了c=0的情况.当c=0时,ac2=bc2.防范措施是使用不等式的性质时,不可忽视条件.
正解:因为c2≥0,且a>b,所以ac2≥bc2,故应填≥.
2.若A=a2+3ab,B=4ab-b2,则A,B的大小关系是( )
A.A≤B B.A≥B
C.A>B D.大小关系不确定
错因分析
因忽视配方法在判断符号中的应用致错
错解:因为A-B=a2+3ab-4ab+b2=a2+b2-ab,所以A,B的大小关系不确定.
B
防范措施
1.用作差法比较两个数(式)的大小时,其关键是变形,一般采用配方、因式分解、通分、有理化等手段变形,这样有利于定号.特别是作差后的式子为二次三项式时,常考虑因式分解或配方法变形.
2.注意培养逻辑推理素养和数学运算素养.
归纳总结
分层练习-基础
D
分层练习-基础
D
分层练习-基础
A
分层练习-基础
A
分层练习-基础
D
分层练习-基础
A
分层练习-基础
C
分层练习-基础
分层练习-基础
<
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
A
分层练习-巩固
分层练习-巩固
B
分层练习-巩固
现实生活中的许多问题能够用不等式解决,其解题思路是将解决的问题转化成不等关系,利用作差法比较大小,进而解决实际问题.
分层练习-巩固
分层练习-拓展
分层练习-拓展
2.有一批衬衣原价为每件80元,甲、乙两商场均有销售.现在每个商场都推出了促销政策:到甲商场买一件衬衣优惠4元,买两件每件优惠8元,买三件每件优惠12元,……依此类推,直至减到半价为止;乙商场则一律按原价7折酬宾.某单位欲为每位员工购买一件该衬衣,问:到哪个商场购买比较合算?
解:设该单位共需购买x件衬衣,在甲、乙两商场购买分别需付款y元、z元.依题意,有
z=80×70%x=56x(x≥1,x∈Z).
分层练习-拓展
①若1≤x≤10,x∈Z,则y-z=(80-4x)x-56x=4x(6-x).
当1≤x≤5,x∈Z时,6-x>0,∴y-z>0,即y>z.
当x=6时,y-z=0,即y=z.
当7≤x≤10,x∈Z时,6-x<0,
∴y-z<0,即y<z.
②若x>10,x∈Z,则y-z=40x-56x=-16x.
∵-16x<0,∴y<z.
综上,若单位人数不超过5人,到乙商场购买合算;若单位人数恰为6人,到甲、乙商场购买一样合算;若单位人数超过6人,到甲商场购买更合算.
分层练习-拓展
分层练习-拓展
分层练习-拓展
不等关系与
比较大小
利用不等式表示不等关系
比较大小
作差法:通常利用配方法化成完全平方式与0比较
作商法:适用于同号的式子作商与1比较
比较大小常用方法
(1)利用不等式时,要注意等号能否取到
(2)利用不等式表示不等关系时要注意实际意义
数学建模:用不等式(组)表示实际问题,培养数学建模的核心素养
逻辑推理:通过等式性质类比推理得不等式的性质,培养逻辑推理的核心素养
方法总结
核心知识
易错提醒
核心素养
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
