人教A版高中数学必修第一册第二章一元二次函数、方程和不等式2.1等式性质与不等式性质(第2课时)课件(共59张PPT)
文档属性
| 名称 | 人教A版高中数学必修第一册第二章一元二次函数、方程和不等式2.1等式性质与不等式性质(第2课时)课件(共59张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 00:00:00 | ||
图片预览










文档简介
(共59张PPT)
人教版2019高一数学(必修一)第一章 一元二次函数、方程和不等式
第二课时 等式性质与不等式性质
2.1 等式性质与不等式性质
学习目标
1. 掌握等式性质与不等式性质以及推论,能够运用其解决简单的问题;
2. 进一步掌握作差、作商、综合法等比较法比较实数的大小;
3. 通过教学培养学生合作交流的意识和大胆猜测、乐于探究的良好思维品质.
情景导入
关于两个实数大小关系的基本事实为研究基本不等式的性质奠定了基础.
那么,不等式到底有哪些性质呢?
因为不等式与等式一样,都是对大小关系的刻画,所以我们可以从等式的性质及其研究方法中获得启发.
提示:运算中的不变性就是性质.
我们先来回顾一下等式有哪些性质?
1.探究不等式的性质
新知探究
可以发现,性质1,2反映了相等关系自身的性质,性质3,4,5是从运算的角度提出的,反映了等式在运算中保持的不变性.
类比等式的基本性质,你能猜想不等式的基本性质吗,并加以证明吗?
等式 不等式
对称性
传递性
类比等式的性质1,2,可以猜想不等式有如下性质:
等式 不等式
可加性
A
B
a
b
x
b+c
B1
a+c
A1
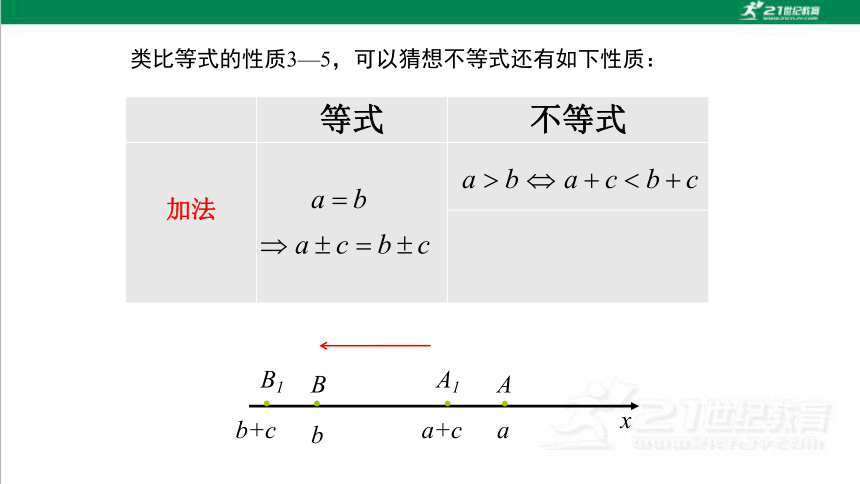
类比等式的性质3—5,可以猜想不等式还有如下性质:
等式 不等式
加法
A
B
a
b
x
b+c
B1
a+c
A1
类比等式的性质3—5,可以猜想不等式还有如下性质:
A
B
a
b
x
b+c
B1
a+c
A1
A
B
a
b
x
b+c
B1
a+c
A1
等式 不等式
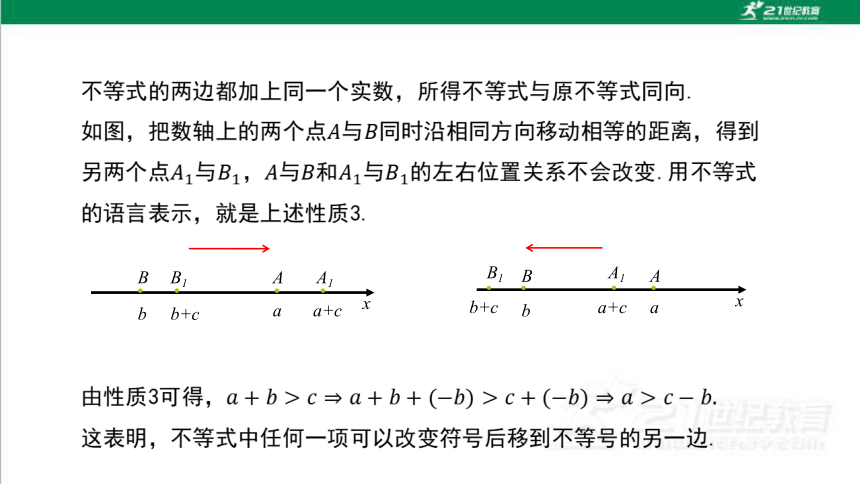
加法
同向可加性:
等式 不等式
乘法
同向同正可乘性、同乘方性:
因此我们可以得到不等式的七个性质:
性质1:如果a>b,那么b<a;
性质2:如果a>b,b>c,那么a>c;
性质3:如果a>b,那么a+c>b+c;
性质4:如果a>b,c>0,那么ac>bc ,如果a>b,c<0,那么ac<bc;
性质5:如果a>b,c>d,那么a+c>b+d;
性质6:如果a>b>0,c>d>0,那么ac>bd;
性质7:如果a>b>0,那么an>bn(n∈N*,n≥2).
概念归纳
实数大小关系的基本事实和不等式的性质是解决不等式问题的基本依据.
利用不等式性质判断不等式是否成立的方法:
(1)运用不等式的性质判断:要注意不等式成立的条件,不要弱化条件,尤其是不能凭想象捏造性质;
(2)特殊值法:取特殊值时,要遵循如下原则:一是满足题设条件;二是取值要简单,便于验证计算。尤其是在选择题中经常采用这种方法。
概念归纳
例2.已知a>b>0,c<0,求证: .
课本例题
证明:∵a>b>0,
于是 ,即 .
又由c<0,得 .
∴ab>0, ,
探究一 不等式的性质及应用
典例剖析
典例剖析
典例剖析
利用不等式性质解题的策略
(1)首先要注意不等式成立的条件,不要弱化条件.
(2)解决有关不等式选择题时,也可采用特值法进行排除,注意取值要遵循以下原则:一是满足题设条件;二是取值要简单,便于验证计算.
(3)若要判断某结论正确,应说明理由或进行证明,推理过程应紧扣有关定理、性质等,若要说明某结论错误,只需举一个反例.
概念归纳
【例2】 判断下列四个命题的真假:
(1)若a(2)若a>b>c,则有a|c|>b|c|;
(3)若a>b,cb-d;
(4)若b1,且n为奇数,则有an>bn.
典例剖析
探究二 利用不等式的性质判断命题的真假
∴(1)是假命题.
(2)∵a>b,|c|≥0,
当c≠0时,|c|>0,∴a|c|>b|c|.
当c=0时,|c|=0,∴a|c|=b|c|=0.
∴(2)是假命题.
典例剖析
(3)∵c-d.
又a>b,∴a+(-c)>b+(-d).
即a-c>b-d.∴(3)是真命题.
(4)当b-a>0.
∴(-b)n>(-a)n.
∵n为奇数,∴-bn>-an.∴an>bn.
∴(4)是真命题.
典例剖析
运用不等式的性质判断时,要注意不等式成立的条件,不要弱化条件,尤其是不能凭想当然随意捏造性质.解有关不等式的选择题时,也可采用特殊值法进行排除,注意取值一定要遵循如下原则:一是满足题设条件;二是取值要简单,便于验证计算.
概念归纳
练一练
D
练一练
练一练
【例3】 (1)已知a>b,e>f,c>0,求证:f-ac分析:根据条件选择合适的不等式的基本性质证明有关不等式.
典例剖析
探究三 利用不等式的性质证明不等式
典例剖析
用不等式的性质进行证明时,要善于寻找欲证不等式与已知条件的关系,利用相应的不等式性质证明;
要注意观察一个不等式是不是在某个已知条件的两边同乘(除以)一个常数;
一个不等式是不是某两个同向不等式相加得到的;
一个不等式是不是将一个不等式的两边取了倒数而得到的等等.
概念归纳
练一练
解:(1)因为-1(2)由-1典例剖析
探究四 利用不等式的性质求取值范围
【例4】 已知-1(1)求x-y的取值范围;
(2)求3x+2y的取值范围.
解:因为-1又因为x3.已知“-1求x-y的取值范围;
1.利用几个不等式的取值范围来确定某代数式的取值范围是一类常见的综合问题,解题时要紧扣不等式的基本性质,不能直接将几个已知不等式相加(减或相乘除).
2.注意培养逻辑推理素养和数学运算素养.
练一练
随堂练
B
随堂练
C
3.若1≤a≤5,-1≤b≤2,则a-b的取值范围是 .
解析:∵-1≤b≤2,∴-2≤-b≤1.
又1≤a≤5,∴-1≤a-b≤6.
随堂练
-1≤a-b≤6
随堂练
课本练习
错用不等式的性质
1.已知1≤a-b≤2,且2≤a+b≤4,求4a-2b的取值范围.
错解:1≤a-b≤2,①
2≤a+b≤4,②
错因分析
这个方法错在哪里?
提示:上面的解法看上去似乎每一步都是合情合理的,但实际上答案是错误的.
那到底是为什么呢
我们先看不等式4a-2b ≥3什么时候取等号,
由上述解题过程可知,当 ,才取等号,而此时a-b=0,不满足①式,
因此4a-2b是不能等于3的.同理可验证4a-2b也不能等于12.
出现上述错误的原因是“同向不等式两边分别相加所得不等式与原不等式同向”这一性质是单向的,用它来做变形,是非同解变形,因此结论是错误的.
归纳总结
错因分析
防范措施
1.建立待求取值范围的整体与已知取值范围的整体的关系,利用不等式的性质进行运算,求得待求的取值范围.
2.同向(异向)不等式的两边可以相加(减),但这种转化不是等价变形,如果在解题过程中多次使用这种转化,就有可能扩大其取值范围,所以我们选用不等式的性质求代数式的取值范围时务必小心谨慎,必要时改换求解的思路和方法.
归纳总结
4.已知-1练一练
分层练习-基础
分层练习-基础
分层练习-基础
③
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-拓展
分层练习-拓展
分层练习-拓展
1≤α+3β≤7
分层练习-拓展
C
课堂小结
不等式
的性质
核心知识
方法总结
易错提醒
核心素养
利用不等式性质判断正误的方法:
(1)直接法:正确的说法利用不等式的相关性质或函数的相关性质证明; 说法错误的只需举出一个反例即可。
(2)特殊值法:取值的原则:一是满足题设条件;二是取值要简单,便于验证计算;三是所取的值要有代表性.
(1)不等式两边同乘或除以负数时,要变号;
(2)同乘或除以代数式时,要注意代数式的正负分类讨论
逻辑推理:通过等式性质,类比推理不等式性质,培养逻辑推理的核心素养
数学建模:不等式的实际应用,培养数学建模的核心素养
对称性,传递性
同加保序性
乘正保序性
移项法则
正数同向可乘性
乘负反序性
正数乘方保序性
人教版2019高一数学(必修一)第一章 一元二次函数、方程和不等式
第二课时 等式性质与不等式性质
2.1 等式性质与不等式性质
学习目标
1. 掌握等式性质与不等式性质以及推论,能够运用其解决简单的问题;
2. 进一步掌握作差、作商、综合法等比较法比较实数的大小;
3. 通过教学培养学生合作交流的意识和大胆猜测、乐于探究的良好思维品质.
情景导入
关于两个实数大小关系的基本事实为研究基本不等式的性质奠定了基础.
那么,不等式到底有哪些性质呢?
因为不等式与等式一样,都是对大小关系的刻画,所以我们可以从等式的性质及其研究方法中获得启发.
提示:运算中的不变性就是性质.
我们先来回顾一下等式有哪些性质?
1.探究不等式的性质
新知探究
可以发现,性质1,2反映了相等关系自身的性质,性质3,4,5是从运算的角度提出的,反映了等式在运算中保持的不变性.
类比等式的基本性质,你能猜想不等式的基本性质吗,并加以证明吗?
等式 不等式
对称性
传递性
类比等式的性质1,2,可以猜想不等式有如下性质:
等式 不等式
可加性
A
B
a
b
x
b+c
B1
a+c
A1
类比等式的性质3—5,可以猜想不等式还有如下性质:
等式 不等式
加法
A
B
a
b
x
b+c
B1
a+c
A1
类比等式的性质3—5,可以猜想不等式还有如下性质:
A
B
a
b
x
b+c
B1
a+c
A1
A
B
a
b
x
b+c
B1
a+c
A1
等式 不等式
加法
同向可加性:
等式 不等式
乘法
同向同正可乘性、同乘方性:
因此我们可以得到不等式的七个性质:
性质1:如果a>b,那么b<a;
性质2:如果a>b,b>c,那么a>c;
性质3:如果a>b,那么a+c>b+c;
性质4:如果a>b,c>0,那么ac>bc ,如果a>b,c<0,那么ac<bc;
性质5:如果a>b,c>d,那么a+c>b+d;
性质6:如果a>b>0,c>d>0,那么ac>bd;
性质7:如果a>b>0,那么an>bn(n∈N*,n≥2).
概念归纳
实数大小关系的基本事实和不等式的性质是解决不等式问题的基本依据.
利用不等式性质判断不等式是否成立的方法:
(1)运用不等式的性质判断:要注意不等式成立的条件,不要弱化条件,尤其是不能凭想象捏造性质;
(2)特殊值法:取特殊值时,要遵循如下原则:一是满足题设条件;二是取值要简单,便于验证计算。尤其是在选择题中经常采用这种方法。
概念归纳
例2.已知a>b>0,c<0,求证: .
课本例题
证明:∵a>b>0,
于是 ,即 .
又由c<0,得 .
∴ab>0, ,
探究一 不等式的性质及应用
典例剖析
典例剖析
典例剖析
利用不等式性质解题的策略
(1)首先要注意不等式成立的条件,不要弱化条件.
(2)解决有关不等式选择题时,也可采用特值法进行排除,注意取值要遵循以下原则:一是满足题设条件;二是取值要简单,便于验证计算.
(3)若要判断某结论正确,应说明理由或进行证明,推理过程应紧扣有关定理、性质等,若要说明某结论错误,只需举一个反例.
概念归纳
【例2】 判断下列四个命题的真假:
(1)若a
(3)若a>b,c
(4)若b
典例剖析
探究二 利用不等式的性质判断命题的真假
∴(1)是假命题.
(2)∵a>b,|c|≥0,
当c≠0时,|c|>0,∴a|c|>b|c|.
当c=0时,|c|=0,∴a|c|=b|c|=0.
∴(2)是假命题.
典例剖析
(3)∵c
又a>b,∴a+(-c)>b+(-d).
即a-c>b-d.∴(3)是真命题.
(4)当b
∴(-b)n>(-a)n.
∵n为奇数,∴-bn>-an.∴an>bn.
∴(4)是真命题.
典例剖析
运用不等式的性质判断时,要注意不等式成立的条件,不要弱化条件,尤其是不能凭想当然随意捏造性质.解有关不等式的选择题时,也可采用特殊值法进行排除,注意取值一定要遵循如下原则:一是满足题设条件;二是取值要简单,便于验证计算.
概念归纳
练一练
D
练一练
练一练
【例3】 (1)已知a>b,e>f,c>0,求证:f-ac
典例剖析
探究三 利用不等式的性质证明不等式
典例剖析
用不等式的性质进行证明时,要善于寻找欲证不等式与已知条件的关系,利用相应的不等式性质证明;
要注意观察一个不等式是不是在某个已知条件的两边同乘(除以)一个常数;
一个不等式是不是某两个同向不等式相加得到的;
一个不等式是不是将一个不等式的两边取了倒数而得到的等等.
概念归纳
练一练
解:(1)因为-1
探究四 利用不等式的性质求取值范围
【例4】 已知-1
(2)求3x+2y的取值范围.
解:因为-1
1.利用几个不等式的取值范围来确定某代数式的取值范围是一类常见的综合问题,解题时要紧扣不等式的基本性质,不能直接将几个已知不等式相加(减或相乘除).
2.注意培养逻辑推理素养和数学运算素养.
练一练
随堂练
B
随堂练
C
3.若1≤a≤5,-1≤b≤2,则a-b的取值范围是 .
解析:∵-1≤b≤2,∴-2≤-b≤1.
又1≤a≤5,∴-1≤a-b≤6.
随堂练
-1≤a-b≤6
随堂练
课本练习
错用不等式的性质
1.已知1≤a-b≤2,且2≤a+b≤4,求4a-2b的取值范围.
错解:1≤a-b≤2,①
2≤a+b≤4,②
错因分析
这个方法错在哪里?
提示:上面的解法看上去似乎每一步都是合情合理的,但实际上答案是错误的.
那到底是为什么呢
我们先看不等式4a-2b ≥3什么时候取等号,
由上述解题过程可知,当 ,才取等号,而此时a-b=0,不满足①式,
因此4a-2b是不能等于3的.同理可验证4a-2b也不能等于12.
出现上述错误的原因是“同向不等式两边分别相加所得不等式与原不等式同向”这一性质是单向的,用它来做变形,是非同解变形,因此结论是错误的.
归纳总结
错因分析
防范措施
1.建立待求取值范围的整体与已知取值范围的整体的关系,利用不等式的性质进行运算,求得待求的取值范围.
2.同向(异向)不等式的两边可以相加(减),但这种转化不是等价变形,如果在解题过程中多次使用这种转化,就有可能扩大其取值范围,所以我们选用不等式的性质求代数式的取值范围时务必小心谨慎,必要时改换求解的思路和方法.
归纳总结
4.已知-1
分层练习-基础
分层练习-基础
分层练习-基础
③
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-基础
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-巩固
分层练习-拓展
分层练习-拓展
分层练习-拓展
1≤α+3β≤7
分层练习-拓展
C
课堂小结
不等式
的性质
核心知识
方法总结
易错提醒
核心素养
利用不等式性质判断正误的方法:
(1)直接法:正确的说法利用不等式的相关性质或函数的相关性质证明; 说法错误的只需举出一个反例即可。
(2)特殊值法:取值的原则:一是满足题设条件;二是取值要简单,便于验证计算;三是所取的值要有代表性.
(1)不等式两边同乘或除以负数时,要变号;
(2)同乘或除以代数式时,要注意代数式的正负分类讨论
逻辑推理:通过等式性质,类比推理不等式性质,培养逻辑推理的核心素养
数学建模:不等式的实际应用,培养数学建模的核心素养
对称性,传递性
同加保序性
乘正保序性
移项法则
正数同向可乘性
乘负反序性
正数乘方保序性
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
