人教A版高中数学必修第一册第三章函数的概念与性质3.2.1单调性与最大(小)值(第2课时 函数的最大值、最小值)课件最小值)课件(共29张PPT)
文档属性
| 名称 | 人教A版高中数学必修第一册第三章函数的概念与性质3.2.1单调性与最大(小)值(第2课时 函数的最大值、最小值)课件最小值)课件(共29张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 09:35:34 | ||
图片预览





文档简介
(共29张PPT)
人教A版2019高一数学(必修一)第三章 函数的概念与性质
3.2.1 单调性与最大(小)值
第2课时 函数的最大值、最小值
1.理解函数的最大值和最小值的概念及其几何意义.(重点)
2.能借助函数的图象和单调性,求一些简单函数的最值.(重点、难点)
3.能利用函数的最值解决有关的实际应用问题.(重点)
4.通过本节内容的学习,使学生体会数形结合思想、分类讨论思想在求解最值中的作用,提高学生逻辑推理、数学运算的能力.(重点、难点)
学习目标
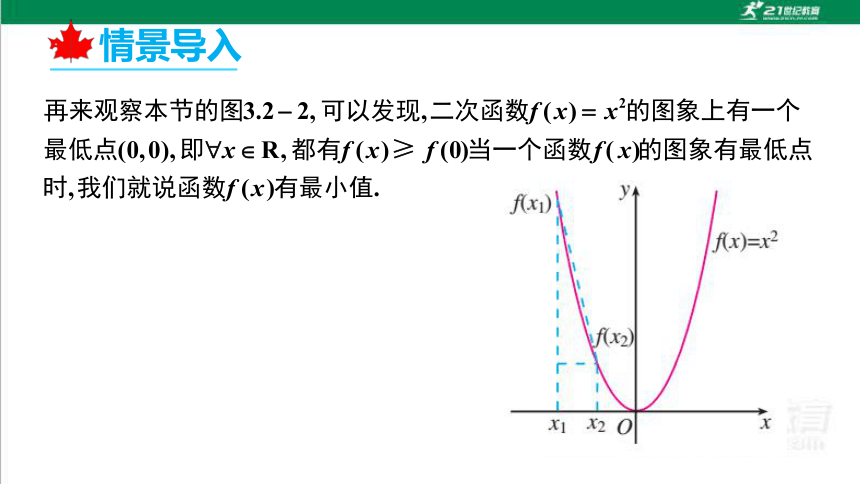
情景导入
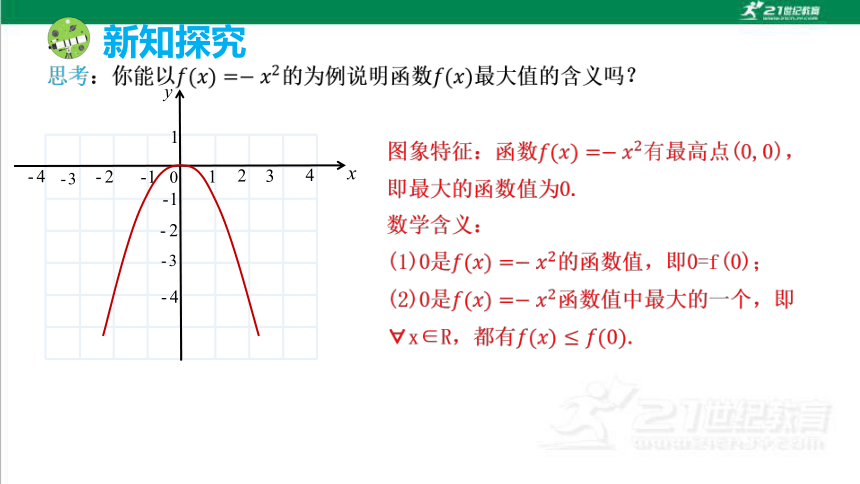
新知探究
函数最大值概念:
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
(1)对于任意的x∈I,都有f(x)≤M;
(2)存在x0∈I,使得f(x0) = M
那么,称M是函数y=f(x)的最大值
新知探究
一般地,设函数y=f(x)的定义域为I,如果实数M满足:
(1)对于任意的的x∈I,都有f(x) ≥ M;
(2)存在 ,使得
那么我们称M是函数y=f(x)的最小值(minimun value).
新知探究
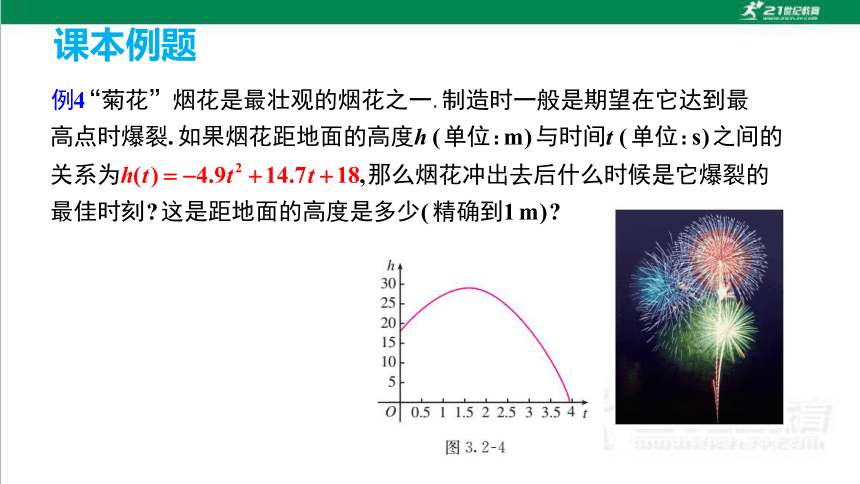
课本例题
烟花设计者就是按照这些数据设定引信的长度,以达到施放烟花的最佳效果.
即 烟花冲出后1.5s是它爆裂的最佳时刻,这时距地面的高度约为29m.
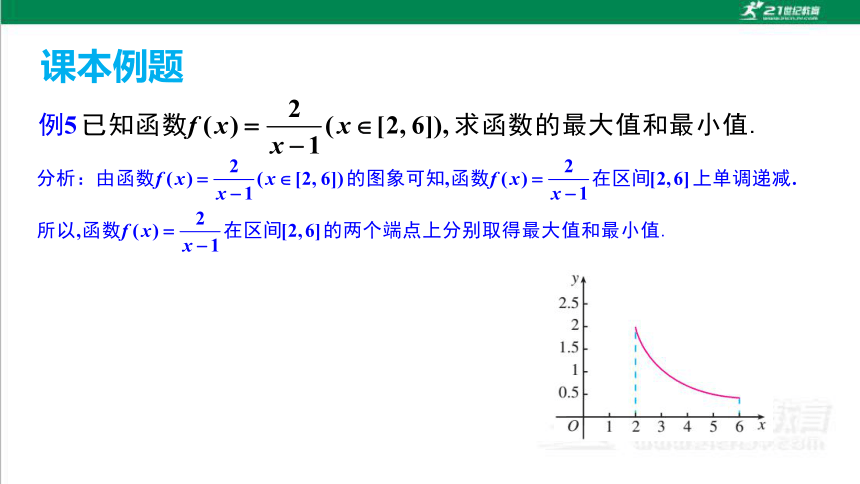
课本例题
课本例题
课本例题
1.整个上午(8:00~12:00)天气越来越暖,中午时分(12:00~13:00)一场暴风雨使天气骤然凉爽了许多.暴风雨过后,天气转暖,直到太阳落山(18:00)才开始转凉.画出这一天8:00~20:00期间气温作为时间函数的一个可能的图象(示意图),并说出所画函数的单调区间.
课本练习
最小值
课本练习
课本练习
易错警示 忽视单调性致误
错因分析
若f(x)=x2-6x+m在区间[2,+∞)上的最小值为-3,则m=________.
错解:由于f(x)在区间[2,+∞)上的最小值为3,所以f(2)=4-12+m=-3,即m=5.
易错防范:由于f(x)图象的对称轴为x=3∈[2,+∞),所以f(x)在x=3时取得最小值,错因在于没有考虑f(x)的单调性.防范措施是研究二次函数在给定区间上的性质必须数形结合,从单调性入手.
正解:由于f(x)图象的对称轴是x=3,所以f(x)在区间[2,3]上单调递减,在区间[3,+∞)上单调递增,故x=3时f(x)最小,f(3)=-9+m=-3,即m=6.
典例剖析
归纳总结
典例剖析
归纳总结
典例剖析
归纳总结
典例剖析
归纳总结
典例剖析
归纳总结
典例剖析
归纳总结
函数的最大
值、最小值
核心知识
方法总结
易错提醒
核心素养
最值M一定是一个函数值,是值域中的一个元素
在利用单调性求最值时,勿忘求函数的定义域
直观想象:通过数形结合法求函数最大值与最小值,培养直观想象的核心素养
函数最值的求法
(1)图象法:对已知函数图象的用此法.
(2)配方法:对二次或通过换元得到的二次型函数适用
(3)单调性法:适用于可判断在闭区间上单调的函数
求解方法
概念
最大值
最小值
课堂小结
人教A版2019高一数学(必修一)第三章 函数的概念与性质
3.2.1 单调性与最大(小)值
第2课时 函数的最大值、最小值
1.理解函数的最大值和最小值的概念及其几何意义.(重点)
2.能借助函数的图象和单调性,求一些简单函数的最值.(重点、难点)
3.能利用函数的最值解决有关的实际应用问题.(重点)
4.通过本节内容的学习,使学生体会数形结合思想、分类讨论思想在求解最值中的作用,提高学生逻辑推理、数学运算的能力.(重点、难点)
学习目标
情景导入
新知探究
函数最大值概念:
一般地,设函数y=f(x)的定义域为I,如果存在实数M满足:
(1)对于任意的x∈I,都有f(x)≤M;
(2)存在x0∈I,使得f(x0) = M
那么,称M是函数y=f(x)的最大值
新知探究
一般地,设函数y=f(x)的定义域为I,如果实数M满足:
(1)对于任意的的x∈I,都有f(x) ≥ M;
(2)存在 ,使得
那么我们称M是函数y=f(x)的最小值(minimun value).
新知探究
课本例题
烟花设计者就是按照这些数据设定引信的长度,以达到施放烟花的最佳效果.
即 烟花冲出后1.5s是它爆裂的最佳时刻,这时距地面的高度约为29m.
课本例题
课本例题
课本例题
1.整个上午(8:00~12:00)天气越来越暖,中午时分(12:00~13:00)一场暴风雨使天气骤然凉爽了许多.暴风雨过后,天气转暖,直到太阳落山(18:00)才开始转凉.画出这一天8:00~20:00期间气温作为时间函数的一个可能的图象(示意图),并说出所画函数的单调区间.
课本练习
最小值
课本练习
课本练习
易错警示 忽视单调性致误
错因分析
若f(x)=x2-6x+m在区间[2,+∞)上的最小值为-3,则m=________.
错解:由于f(x)在区间[2,+∞)上的最小值为3,所以f(2)=4-12+m=-3,即m=5.
易错防范:由于f(x)图象的对称轴为x=3∈[2,+∞),所以f(x)在x=3时取得最小值,错因在于没有考虑f(x)的单调性.防范措施是研究二次函数在给定区间上的性质必须数形结合,从单调性入手.
正解:由于f(x)图象的对称轴是x=3,所以f(x)在区间[2,3]上单调递减,在区间[3,+∞)上单调递增,故x=3时f(x)最小,f(3)=-9+m=-3,即m=6.
典例剖析
归纳总结
典例剖析
归纳总结
典例剖析
归纳总结
典例剖析
归纳总结
典例剖析
归纳总结
典例剖析
归纳总结
函数的最大
值、最小值
核心知识
方法总结
易错提醒
核心素养
最值M一定是一个函数值,是值域中的一个元素
在利用单调性求最值时,勿忘求函数的定义域
直观想象:通过数形结合法求函数最大值与最小值,培养直观想象的核心素养
函数最值的求法
(1)图象法:对已知函数图象的用此法.
(2)配方法:对二次或通过换元得到的二次型函数适用
(3)单调性法:适用于可判断在闭区间上单调的函数
求解方法
概念
最大值
最小值
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
