人教A版高中数学必修第一册第四章指数函数与对数函数4.2.2指数函数的图象和性质 课件(共33张PPT)
文档属性
| 名称 | 人教A版高中数学必修第一册第四章指数函数与对数函数4.2.2指数函数的图象和性质 课件(共33张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 09:44:26 | ||
图片预览







文档简介
(共33张PPT)
人教A版2019必修第一册
4.2.2 指数函数的图像和性质
第 4章 指数函数与对数函数
学习目标
1.理解指数函数的概念和意义,会画指数函数的图像。 2.探索并理解指数函数的单调性和特殊点。 3.理解指数函数的图像与性质,能运用指数函数的图像和性质解决有关数学问题。
请同学们回顾一下指数函数的概念?
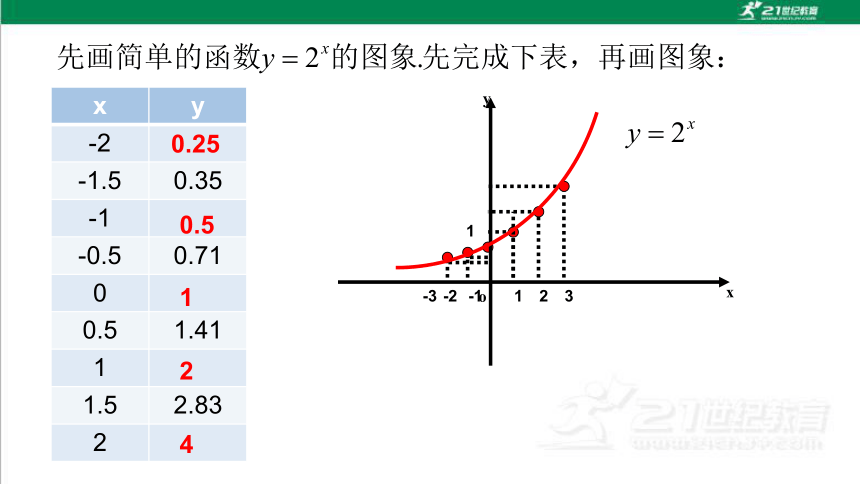
下面我们类比研究幂函数性质的过程与方法,进一步研究指数函数.华罗庚曾说过,“数缺形时少直观,形缺数时难入微”,下面我们尝试画出指数函数的图象,然后借助图象研究指数函数的性质.
你能说说研究函数的一般步骤和方法吗?
我们可以类比研究幂函数性质的过程和方法,进一步研究首先画出指数函数的图象,然后借助图象研究指数函数的性质.
x y
-2
-1.5 0.35
-1
-0.5 0.71
0
0.5 1.41
1
1.5 2.83
2
1
x
y
o
1
2
3
-1
-2
-3
0.25
0.5
1
2
4
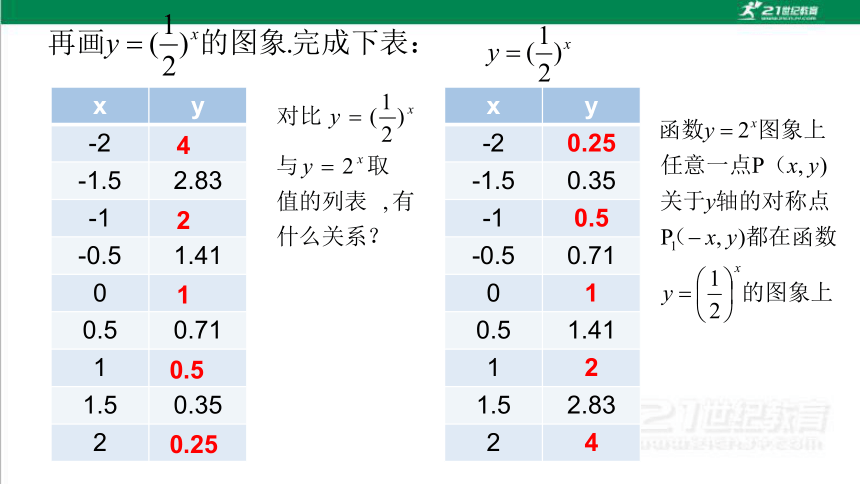
x y
-2
-1.5 2.83
-1
-0.5 1.41
0
0.5 0.71
1
1.5 0.35
2
x y
-2 0.25
-1.5 0.35
-1 0.5
-0.5 0.71
0 1
0.5 1.41
1 2
1.5 2.83
2 4
4
2
1
0.5
0.25
1
x
y
o
1
2
3
-1
-2
-3
a的范围 a>1 0图象
性质 定义域
值域
定点
单调性
函数值
若x>0, 则y>1
若x<0, 则0若x>0, 则0若x<0, 则y>1
R
(0,+∞)
(0,1)
增函数
减函数
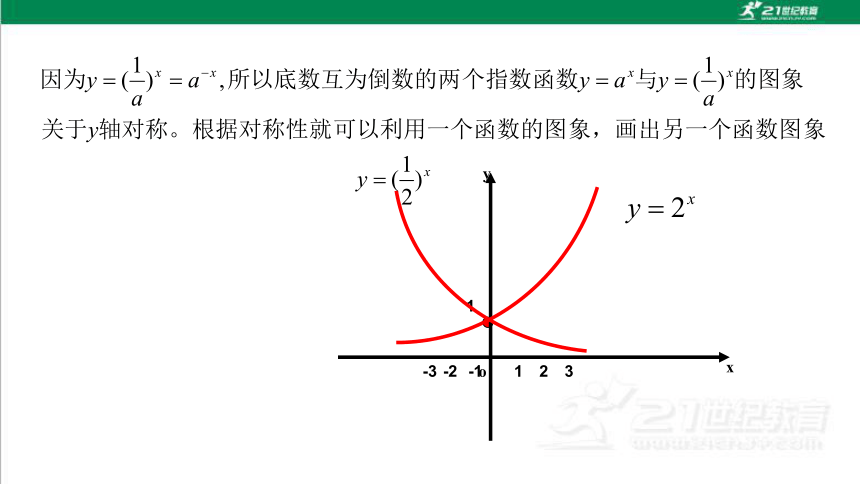
O
x
y
1
O
x
y
1
指数函数的图像和性质
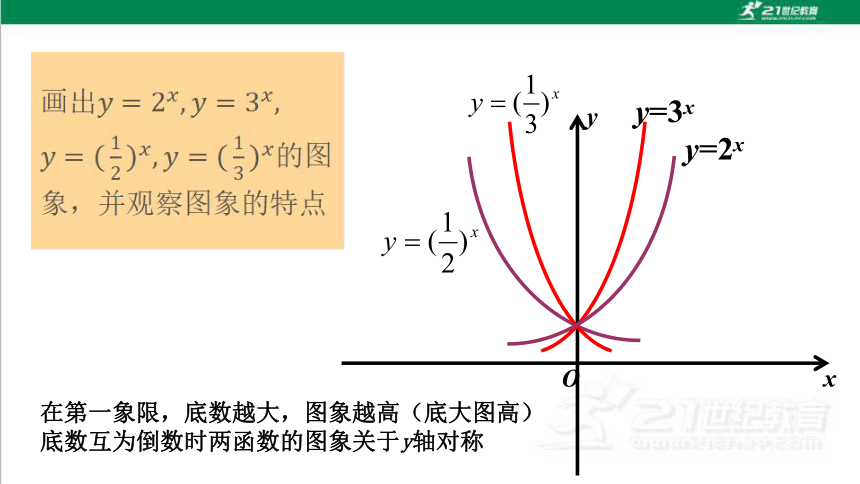
x
O
y
y=3x
y=2x
在第一象限,底数越大,图象越高(底大图高)
底数互为倒数时两函数的图象关于y轴对称
【例3】比较下列各题中两个值的大小.
【解】(1)函数 是增函数,且2.5<3,则1.72.5<1.73
(2)函数 是减函数,且 ,则
(3)
一:比较两个函数值的大小
比较幂的大小的方法
(1)同底数幂比较大小时构造指数函数,根据其单调性比较.
(2)指数相同底数不同时分别画出以两幂底数为底数的指数函
数图象,当x取相同幂指数时可观察出函数值的大小.
(3)底数、指数都不相同时,取与其中一底数相同与另一指数
相同的幂与两数比较,或借助“1”与两数比较.
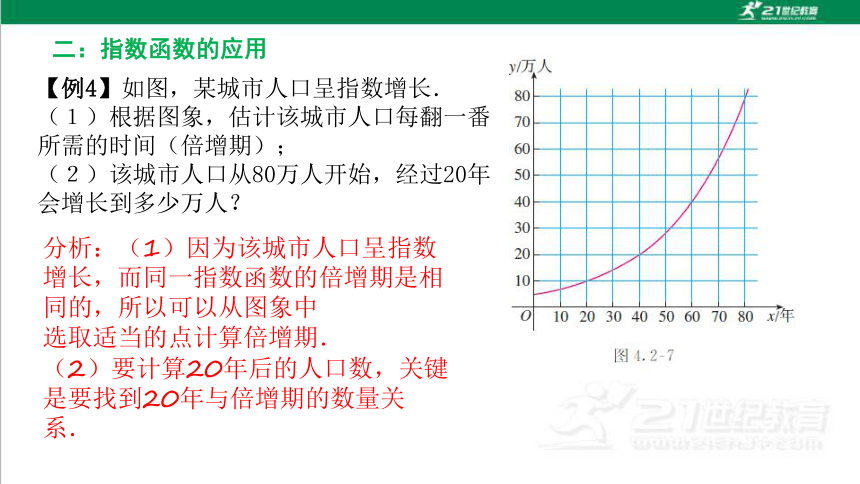
(4)当底数含参数时,要按底数a>1和0【例4】如图,某城市人口呈指数增长.
(1)根据图象,估计该城市人口每翻一番所需的时间(倍增期);
(2)该城市人口从80万人开始,经过20年会增长到多少万人?
分析:(1)因为该城市人口呈指数增长,而同一指数函数的倍增期是相同的,所以可以从图象中
选取适当的点计算倍增期.
(2)要计算20年后的人口数,关键是要找到20年与倍增期的数量关系.
二:指数函数的应用
解:(1)观察图,发现该城市人口经过20年约为10万人,经过40年约为20万人,即由10万人口增加到20万人口所用的时间约为20年,所以该城市人口每翻一番所需的时间约为20年.
(2)因为倍增期为20年,所以每经过20年,人口将翻一番.因此,从80万人开始,经过20年,该城市人口大约会增长到160万人.
课本练习
2:比较下列各题中两个值的大小:
3..人体内的癌细胞初期增加和很缓慢,但到了晚期就急剧增加,试画一幅能反映体内癌细胞数量随时间的变化图。
解:
假设体内的最初的癌细胞数量为k,每过时间t0,1个癌细胞分裂成两个。
则经过时间t,体内癌细胞数量y为
其大致图象如右
题型一:指数函数的定义域和值域
题型分类讲解
题型二:指数函数的图象及应用
指数函数图象问题的处理技巧:
(1)抓住图象上的特殊点,如指数函数的图象恒过定点.
(2)利用图象变换,如函数图象的平移变换(左右平移、上下平移).
(3)利用函数的奇偶性与单调性.奇偶性决定函数图象的走势.
题型三:指数函数的简单应用
随堂检测
a>1 0图
象
性
质 (1)定义域:
(2)值域:
(3)过定点:
(4)单调性: (4)单调性:
(5)奇偶性: (5)奇偶性:
R
(0,+∞)
(0,1)
增函数
减函数
非奇非偶
非奇非偶
(6)当x>0时,y>1.
当x<0时,0(6)当x>o时,0 当x<0时,y>1.
x
y
o
1
x
y
o
1
指数函数图象与性质
课堂小结
2、指数比较大小的方法;
①、构造函数法:要点是利用函数的单调性,数的特征是同底不同指(包括可以化为同底的)。或画图像直接描点观察法。
②、搭桥比较法:用别的数如0或1做桥。数的特征是不同底不同指。
人教A版2019必修第一册
4.2.2 指数函数的图像和性质
第 4章 指数函数与对数函数
学习目标
1.理解指数函数的概念和意义,会画指数函数的图像。 2.探索并理解指数函数的单调性和特殊点。 3.理解指数函数的图像与性质,能运用指数函数的图像和性质解决有关数学问题。
请同学们回顾一下指数函数的概念?
下面我们类比研究幂函数性质的过程与方法,进一步研究指数函数.华罗庚曾说过,“数缺形时少直观,形缺数时难入微”,下面我们尝试画出指数函数的图象,然后借助图象研究指数函数的性质.
你能说说研究函数的一般步骤和方法吗?
我们可以类比研究幂函数性质的过程和方法,进一步研究首先画出指数函数的图象,然后借助图象研究指数函数的性质.
x y
-2
-1.5 0.35
-1
-0.5 0.71
0
0.5 1.41
1
1.5 2.83
2
1
x
y
o
1
2
3
-1
-2
-3
0.25
0.5
1
2
4
x y
-2
-1.5 2.83
-1
-0.5 1.41
0
0.5 0.71
1
1.5 0.35
2
x y
-2 0.25
-1.5 0.35
-1 0.5
-0.5 0.71
0 1
0.5 1.41
1 2
1.5 2.83
2 4
4
2
1
0.5
0.25
1
x
y
o
1
2
3
-1
-2
-3
a的范围 a>1 0
性质 定义域
值域
定点
单调性
函数值
若x>0, 则y>1
若x<0, 则0
R
(0,+∞)
(0,1)
增函数
减函数
O
x
y
1
O
x
y
1
指数函数的图像和性质
x
O
y
y=3x
y=2x
在第一象限,底数越大,图象越高(底大图高)
底数互为倒数时两函数的图象关于y轴对称
【例3】比较下列各题中两个值的大小.
【解】(1)函数 是增函数,且2.5<3,则1.72.5<1.73
(2)函数 是减函数,且 ,则
(3)
一:比较两个函数值的大小
比较幂的大小的方法
(1)同底数幂比较大小时构造指数函数,根据其单调性比较.
(2)指数相同底数不同时分别画出以两幂底数为底数的指数函
数图象,当x取相同幂指数时可观察出函数值的大小.
(3)底数、指数都不相同时,取与其中一底数相同与另一指数
相同的幂与两数比较,或借助“1”与两数比较.
(4)当底数含参数时,要按底数a>1和0
(1)根据图象,估计该城市人口每翻一番所需的时间(倍增期);
(2)该城市人口从80万人开始,经过20年会增长到多少万人?
分析:(1)因为该城市人口呈指数增长,而同一指数函数的倍增期是相同的,所以可以从图象中
选取适当的点计算倍增期.
(2)要计算20年后的人口数,关键是要找到20年与倍增期的数量关系.
二:指数函数的应用
解:(1)观察图,发现该城市人口经过20年约为10万人,经过40年约为20万人,即由10万人口增加到20万人口所用的时间约为20年,所以该城市人口每翻一番所需的时间约为20年.
(2)因为倍增期为20年,所以每经过20年,人口将翻一番.因此,从80万人开始,经过20年,该城市人口大约会增长到160万人.
课本练习
2:比较下列各题中两个值的大小:
3..人体内的癌细胞初期增加和很缓慢,但到了晚期就急剧增加,试画一幅能反映体内癌细胞数量随时间的变化图。
解:
假设体内的最初的癌细胞数量为k,每过时间t0,1个癌细胞分裂成两个。
则经过时间t,体内癌细胞数量y为
其大致图象如右
题型一:指数函数的定义域和值域
题型分类讲解
题型二:指数函数的图象及应用
指数函数图象问题的处理技巧:
(1)抓住图象上的特殊点,如指数函数的图象恒过定点.
(2)利用图象变换,如函数图象的平移变换(左右平移、上下平移).
(3)利用函数的奇偶性与单调性.奇偶性决定函数图象的走势.
题型三:指数函数的简单应用
随堂检测
a>1 0
象
性
质 (1)定义域:
(2)值域:
(3)过定点:
(4)单调性: (4)单调性:
(5)奇偶性: (5)奇偶性:
R
(0,+∞)
(0,1)
增函数
减函数
非奇非偶
非奇非偶
(6)当x>0时,y>1.
当x<0时,0
x
y
o
1
x
y
o
1
指数函数图象与性质
课堂小结
2、指数比较大小的方法;
①、构造函数法:要点是利用函数的单调性,数的特征是同底不同指(包括可以化为同底的)。或画图像直接描点观察法。
②、搭桥比较法:用别的数如0或1做桥。数的特征是不同底不同指。
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
