人教A版高中数学必修第一册第五章三角函数5.4.2正弦、余弦函数的单调性与最值(第2课时)课件(共42张PPT)
文档属性
| 名称 | 人教A版高中数学必修第一册第五章三角函数5.4.2正弦、余弦函数的单调性与最值(第2课时)课件(共42张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 09:59:44 | ||
图片预览









文档简介
(共42张PPT)
人教A版2019必修第一册
第 5章 三角函数
5.4.2 正弦、余弦函数的单调性与最值
(第2课时)
学习目标
1.掌握y=sin x,y=cos x的最大值与最小值,并会求简单三角函数的值域和最值.(重点、难点)
2.掌握y=sin x,y=cos x的单调性,并能利用单调性比较大小.(重点)
3.会求函数y=Asin(ωx+φ)及y=Acos(ωx+φ)的单调区间.(重点、易混点)
x ↗ 0 ↗ ↗ ↗
sin x -1 ↗ 0 ↗ 1 ↘ 0 ↘ -1
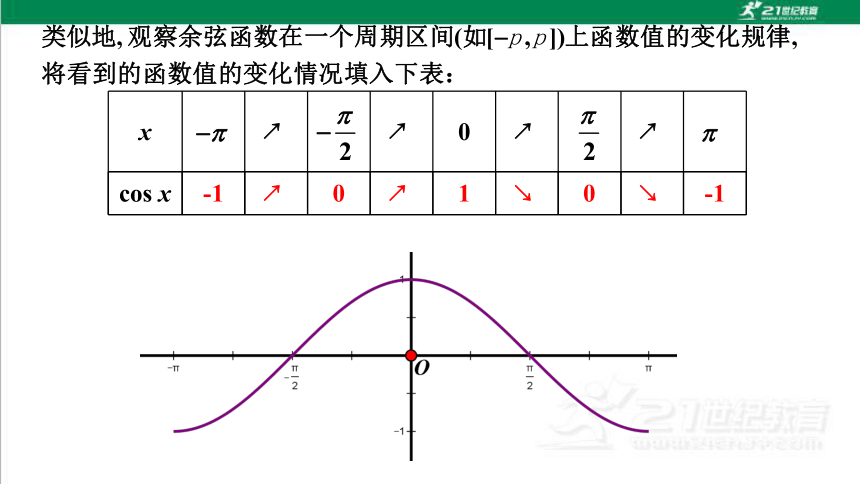
x ↗ ↗ 0 ↗ ↗
cos x
-1 ↗ 0 ↗ 1 ↘ 0 ↘ -1
y
x
o
y
x
o
从上述对正弦函数、余弦函数的单调性的讨论中容易得到,
解: 容易知道,这两个函数都有最大值、最小值.
分析: 可利用三角函数的单调性比较两个同名三角函数值的大小.为此,先用诱导公式将已知角化为同一单调区间内的角,然后再比较大小.
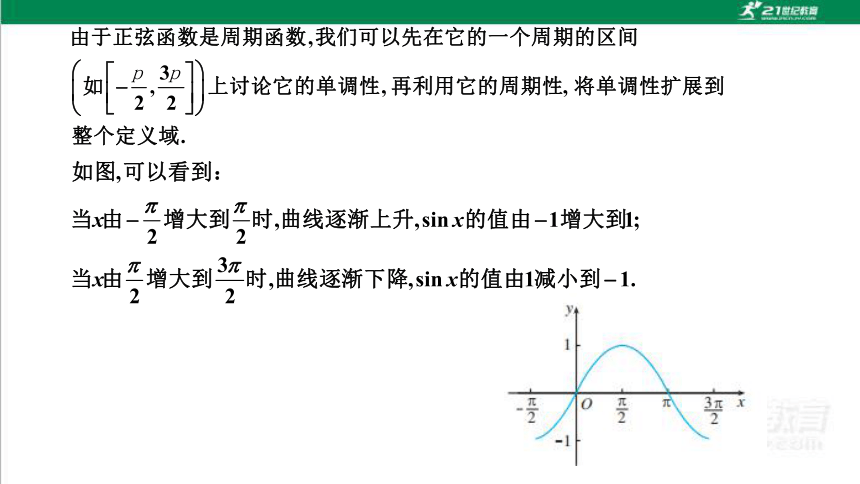
正弦函数的图像
探究
余弦函数的图像
问题:它们的图像有何对称性?
中心对称:将图像绕对称中心旋转180度后所得的曲线能够和原来的曲线重合.
轴对称:将图像绕对称轴折叠180度后所得的曲线能够和原来的曲线重合.
正弦函数的图像
对称轴:
对称中心:
余弦函数的图像
对称轴:
对称中心:
课本练习
u
y
1
-1
O
y=sinx
u
y
1
-1
O
y=sinu
题型一:正弦函数、余弦函数的单调性
题型分类讲解
题型二:正弦函数、余弦函数单调性的应用
题型三:正弦函数、余弦函数的最值问题
随堂检测
1.确定三角函数单调区间的方法有多种,如换元法、列表法、图象法等,解题时需适当选取,同时要注意,求函数的单调区间必须在这个函数的定义域内进行.
2.函数单调性最基本的应用是比较大小与求值域,求三角函数值域的方法很多,如果函数式中含有多个三角函数式,往往要先将函数式进行变形.
课堂小结
人教A版2019必修第一册
第 5章 三角函数
5.4.2 正弦、余弦函数的单调性与最值
(第2课时)
学习目标
1.掌握y=sin x,y=cos x的最大值与最小值,并会求简单三角函数的值域和最值.(重点、难点)
2.掌握y=sin x,y=cos x的单调性,并能利用单调性比较大小.(重点)
3.会求函数y=Asin(ωx+φ)及y=Acos(ωx+φ)的单调区间.(重点、易混点)
x ↗ 0 ↗ ↗ ↗
sin x -1 ↗ 0 ↗ 1 ↘ 0 ↘ -1
x ↗ ↗ 0 ↗ ↗
cos x
-1 ↗ 0 ↗ 1 ↘ 0 ↘ -1
y
x
o
y
x
o
从上述对正弦函数、余弦函数的单调性的讨论中容易得到,
解: 容易知道,这两个函数都有最大值、最小值.
分析: 可利用三角函数的单调性比较两个同名三角函数值的大小.为此,先用诱导公式将已知角化为同一单调区间内的角,然后再比较大小.
正弦函数的图像
探究
余弦函数的图像
问题:它们的图像有何对称性?
中心对称:将图像绕对称中心旋转180度后所得的曲线能够和原来的曲线重合.
轴对称:将图像绕对称轴折叠180度后所得的曲线能够和原来的曲线重合.
正弦函数的图像
对称轴:
对称中心:
余弦函数的图像
对称轴:
对称中心:
课本练习
u
y
1
-1
O
y=sinx
u
y
1
-1
O
y=sinu
题型一:正弦函数、余弦函数的单调性
题型分类讲解
题型二:正弦函数、余弦函数单调性的应用
题型三:正弦函数、余弦函数的最值问题
随堂检测
1.确定三角函数单调区间的方法有多种,如换元法、列表法、图象法等,解题时需适当选取,同时要注意,求函数的单调区间必须在这个函数的定义域内进行.
2.函数单调性最基本的应用是比较大小与求值域,求三角函数值域的方法很多,如果函数式中含有多个三角函数式,往往要先将函数式进行变形.
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
