人教A版高中数学必修第一册第五章三角函数5.7三角函数的应用(第2课时)课件(共24张PPT)
文档属性
| 名称 | 人教A版高中数学必修第一册第五章三角函数5.7三角函数的应用(第2课时)课件(共24张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 821.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-22 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
人教A版2019必修第一册
第 5章 三角函数
5.7三角函数的应用(第2课时)
学习目标
1.了解三角函数是描述周期变化现象的重要函数模型,并会用三角函数模型解决一些简单的实际问题.(重点)
2.实际问题抽象为三角函数模型.(难点)
生活中普遍存在着周期性变化规律的现象,昼夜交替、四季轮回,潮涨潮散、云卷云舒,情绪的起起落落,庭前的花开花谢,一切都逃不过数学的眼睛!这节课我们就来学习如何用数学的眼睛洞察我们身边存在的周期现象。
匀速圆周运动、简谐运动和交变电流都是理想化的运动变化现象,可以用三角函数模型准确的描述它们的运动变化.在现实生活中也有大量运动变化现象,仅在一定范围内呈现出近似于周期变化特点,这些现象也可以借助三角函数近似的描述.
情景导入
例1.如图,某地一天从6~14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.
(1)求这一天6~14时的最大温差;
(2)写出这段曲线的函数解析式.
问题1:如何根据温度变化曲线得到这一天6~14时的最大温差?
问题2:如何求温度随时间的变化满足的函数关系“y=Asin(ωx+φ)+b”中A,ω, φ ,b的值?
图形中的最高点的纵坐标减去最低点的纵坐标就是这一天6~14时的最大温差,观察图形得出这段时间的最大温差为20℃.
(2)由图可知,
注意自变量的变化范围.
例2.海水受日月的引力,在一定的时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天的时间与水深关系表:
(1)选用一个函数来近似描述这个港口的水深与时间的函数关系,给出整点时的水深的近似值(精确到0.001 m).
(2)一条货船的吃水深度(船底与水面的距离)为4 m,安全条例规定至少要有1.5 m的安全间隙(船底与海底的距离),该船何时能进入港口?在港口能呆多久?
(3)若船的吃水深度为4 m,安全间隙为1.5 m,该船在两点开始卸货,吃水深度以0.3 m/h的速度减少,如果这条船停止卸货后需 0.4 h 才能驶到深水域,那么该船在什么时间必修停止卸货,将船驶向较深的水域?
思考1:观察表格中的数据,每天水深的变化具有什么规律性?
呈周期性变化规律.
思考2:设想水深y是时间x的函数,作出表中的数据对应的散点图,你认为可以用哪个类型的函数来拟合这些数据?
从散点图的形状可以判断,这个港口的水深y与时间x的关系可以用形如y=Asin(ωx+φ)+h的函数来刻画.
(1)选用一个函数来近似描述这个港口的水深与时间的函数关系,给出整点时的水深的近似值(精确到0.001 m).
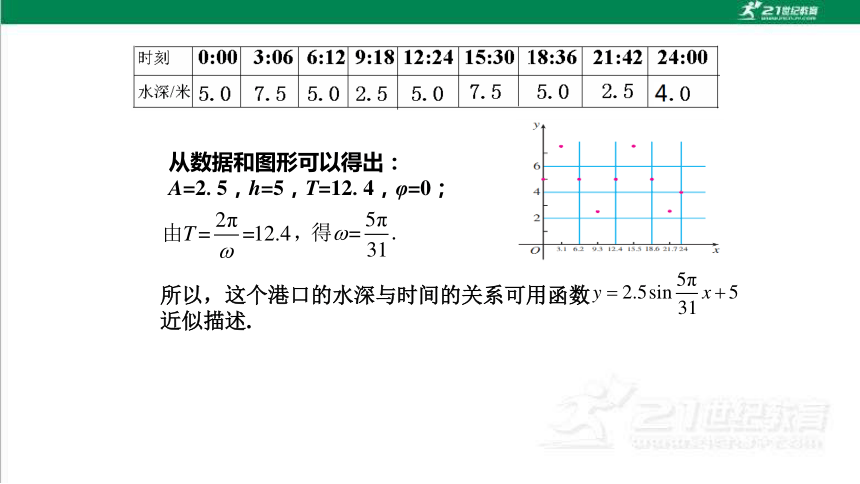
从数据和图形可以得出:
A=2.5,h=5,T=12.4,φ=0;
所以,这个港口的水深与时间的关系可用函数
近似描述.
(2)一条货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与洋底的距离),该船何时能进入港口?在港口能呆多久?
思考3:(2)中,货船需要的安全深度是多少?从函数的解析式来看,满足怎样的条件时,该船能够进入港口?从图象上看呢?
货船需要的安全水深为4+1.5=5.5 m.从函数的解析式来看,满足y≥5.5,即2.5sin x+5≥5.5,该船能够进入港口;从图象上看,就是函数y=2.5sin x+5的图象在直线y=5.5上方时,该船能够进入港口.
利用信息技术绘出两个函数的图象,如下图.
求得交点的横坐标分别为:
xA≈0.3975,xB≈5.8025,xC≈12.7975,xD≈18.2025.
xC,xD也可由函数的周期性得到:
xC≈12.4+0.3975=12.7975,xD≈12.4+5.8025=18.2025.
因此,货船可以在零时30分左右进港,早晨5时45分左右出港;或在下午13时左右进港,下午18时左右出港.每次可以在港口停留5小时左右.
事实上为了安全,进港时间要比算出的时间推后一些,出港时间要比算出的时间提前一些,这样才能保证货船始终在安全水域.
(3)若船的吃水深度为4 m,安全间隙为1.5 m,该船在两点开始卸货,吃水深度以0.3 m/h的速度减少,如果这条船停止卸货后需 0.4 h 才能驶到深水域,那么该船在什么时间必修停止卸货,将船驶向较深的水域?
思考4:(3)中,设在x h时货船的安全水深为y m,y与时间x满足怎样的函数关系?从解析式来看,满足怎样的条件时,该船必须停止卸货?从图象上看呢?
设在x h时货船的安全水深为y m,那么y=5.5-0.3(x-2)(x≥2).
从函数的解析式来看,满足y≥5.5-0.3(x-2),即
2.5sin x+5≥5.5-0.3(x-2)时,该船能够进入港口;
从图象上看,就是函数y=2.5sin x+5的图象在
直线y=5.5-0.3(x-2)上方时,该船能够进入港口.
利用信息技术绘出两个函数的图象,如下图:
可以看到在6~8时之间两个函数只有一个交点P,
借助计算工具,
用二分法可以求得点 P 的坐标约为(7.016,3.995).
因此为了安全,货船最好在6.6时之前停止卸货,将船驶向较深的水域.
1.图为一向右传播的绳波在某一时刻绳子各店的位置图,经过 周期 后,乙点的位置将移至何处?
乙点的位置将移至它关于x轴的对称点处.
课本练习
【答案】 B
随堂检测
2.从出生之日起,人的情绪、体力、智力等状况就呈周期性变化,根据心理学统计,人体节律分为体力节律,情绪节律,智力节律三种,这些节律的时间周期分别为23天,28天,33天.每个节律周期又分为高潮期,临界日,低潮期三个阶段.节律周期的半数为临界日,临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),请根据自己的出生日期,绘制自己的体力,情绪,智力曲线,并预测本学期期末考试期间,你在体力,情绪,智力方面会有怎样的表现,需要注意哪些问题?
解答:由题可知,三个节律曲线的函数模型为y=Asin ωx的形式,
为了研究的方便,我们可以统一设A=10,
象进行分析.
数得到三个自变量,
计算从出生日到本学期期末考试三天的天
观察相应变量区间的三个节律曲线的函数图
以出生日为自变量1,
由节律的时间周期分
别为23天,28天,33天可得相应解析式中的ω值分别为 .
生活中哪类问题可以利用三角函数模型解决?利用三角函数解决实际问题的一般步骤是怎样的?你能够将本节课所学内容画出一个知识结构图吗?其中涉及到哪些数学思想?通过本节课的学习,你还有哪些收获?
实际问题
三角函数模型
解决三角函数问题
联系实际解决问题
周期性
收集数据画散点图
观察图形函数拟合
周期性
课堂小结
人教A版2019必修第一册
第 5章 三角函数
5.7三角函数的应用(第2课时)
学习目标
1.了解三角函数是描述周期变化现象的重要函数模型,并会用三角函数模型解决一些简单的实际问题.(重点)
2.实际问题抽象为三角函数模型.(难点)
生活中普遍存在着周期性变化规律的现象,昼夜交替、四季轮回,潮涨潮散、云卷云舒,情绪的起起落落,庭前的花开花谢,一切都逃不过数学的眼睛!这节课我们就来学习如何用数学的眼睛洞察我们身边存在的周期现象。
匀速圆周运动、简谐运动和交变电流都是理想化的运动变化现象,可以用三角函数模型准确的描述它们的运动变化.在现实生活中也有大量运动变化现象,仅在一定范围内呈现出近似于周期变化特点,这些现象也可以借助三角函数近似的描述.
情景导入
例1.如图,某地一天从6~14时的温度变化曲线近似满足函数y=Asin(ωx+φ)+b.
(1)求这一天6~14时的最大温差;
(2)写出这段曲线的函数解析式.
问题1:如何根据温度变化曲线得到这一天6~14时的最大温差?
问题2:如何求温度随时间的变化满足的函数关系“y=Asin(ωx+φ)+b”中A,ω, φ ,b的值?
图形中的最高点的纵坐标减去最低点的纵坐标就是这一天6~14时的最大温差,观察图形得出这段时间的最大温差为20℃.
(2)由图可知,
注意自变量的变化范围.
例2.海水受日月的引力,在一定的时候发生涨落的现象叫潮.一般地,早潮叫潮,晚潮叫汐.在通常情况下,船在涨潮时驶进航道,靠近码头;卸货后,在落潮时返回海洋.下面是某港口在某季节每天的时间与水深关系表:
(1)选用一个函数来近似描述这个港口的水深与时间的函数关系,给出整点时的水深的近似值(精确到0.001 m).
(2)一条货船的吃水深度(船底与水面的距离)为4 m,安全条例规定至少要有1.5 m的安全间隙(船底与海底的距离),该船何时能进入港口?在港口能呆多久?
(3)若船的吃水深度为4 m,安全间隙为1.5 m,该船在两点开始卸货,吃水深度以0.3 m/h的速度减少,如果这条船停止卸货后需 0.4 h 才能驶到深水域,那么该船在什么时间必修停止卸货,将船驶向较深的水域?
思考1:观察表格中的数据,每天水深的变化具有什么规律性?
呈周期性变化规律.
思考2:设想水深y是时间x的函数,作出表中的数据对应的散点图,你认为可以用哪个类型的函数来拟合这些数据?
从散点图的形状可以判断,这个港口的水深y与时间x的关系可以用形如y=Asin(ωx+φ)+h的函数来刻画.
(1)选用一个函数来近似描述这个港口的水深与时间的函数关系,给出整点时的水深的近似值(精确到0.001 m).
从数据和图形可以得出:
A=2.5,h=5,T=12.4,φ=0;
所以,这个港口的水深与时间的关系可用函数
近似描述.
(2)一条货船的吃水深度(船底与水面的距离)为4米,安全条例规定至少要有1.5米的安全间隙(船底与洋底的距离),该船何时能进入港口?在港口能呆多久?
思考3:(2)中,货船需要的安全深度是多少?从函数的解析式来看,满足怎样的条件时,该船能够进入港口?从图象上看呢?
货船需要的安全水深为4+1.5=5.5 m.从函数的解析式来看,满足y≥5.5,即2.5sin x+5≥5.5,该船能够进入港口;从图象上看,就是函数y=2.5sin x+5的图象在直线y=5.5上方时,该船能够进入港口.
利用信息技术绘出两个函数的图象,如下图.
求得交点的横坐标分别为:
xA≈0.3975,xB≈5.8025,xC≈12.7975,xD≈18.2025.
xC,xD也可由函数的周期性得到:
xC≈12.4+0.3975=12.7975,xD≈12.4+5.8025=18.2025.
因此,货船可以在零时30分左右进港,早晨5时45分左右出港;或在下午13时左右进港,下午18时左右出港.每次可以在港口停留5小时左右.
事实上为了安全,进港时间要比算出的时间推后一些,出港时间要比算出的时间提前一些,这样才能保证货船始终在安全水域.
(3)若船的吃水深度为4 m,安全间隙为1.5 m,该船在两点开始卸货,吃水深度以0.3 m/h的速度减少,如果这条船停止卸货后需 0.4 h 才能驶到深水域,那么该船在什么时间必修停止卸货,将船驶向较深的水域?
思考4:(3)中,设在x h时货船的安全水深为y m,y与时间x满足怎样的函数关系?从解析式来看,满足怎样的条件时,该船必须停止卸货?从图象上看呢?
设在x h时货船的安全水深为y m,那么y=5.5-0.3(x-2)(x≥2).
从函数的解析式来看,满足y≥5.5-0.3(x-2),即
2.5sin x+5≥5.5-0.3(x-2)时,该船能够进入港口;
从图象上看,就是函数y=2.5sin x+5的图象在
直线y=5.5-0.3(x-2)上方时,该船能够进入港口.
利用信息技术绘出两个函数的图象,如下图:
可以看到在6~8时之间两个函数只有一个交点P,
借助计算工具,
用二分法可以求得点 P 的坐标约为(7.016,3.995).
因此为了安全,货船最好在6.6时之前停止卸货,将船驶向较深的水域.
1.图为一向右传播的绳波在某一时刻绳子各店的位置图,经过 周期 后,乙点的位置将移至何处?
乙点的位置将移至它关于x轴的对称点处.
课本练习
【答案】 B
随堂检测
2.从出生之日起,人的情绪、体力、智力等状况就呈周期性变化,根据心理学统计,人体节律分为体力节律,情绪节律,智力节律三种,这些节律的时间周期分别为23天,28天,33天.每个节律周期又分为高潮期,临界日,低潮期三个阶段.节律周期的半数为临界日,临界日的前半期为高潮期,后半期为低潮期.生日前一天是起始位置(平衡位置),请根据自己的出生日期,绘制自己的体力,情绪,智力曲线,并预测本学期期末考试期间,你在体力,情绪,智力方面会有怎样的表现,需要注意哪些问题?
解答:由题可知,三个节律曲线的函数模型为y=Asin ωx的形式,
为了研究的方便,我们可以统一设A=10,
象进行分析.
数得到三个自变量,
计算从出生日到本学期期末考试三天的天
观察相应变量区间的三个节律曲线的函数图
以出生日为自变量1,
由节律的时间周期分
别为23天,28天,33天可得相应解析式中的ω值分别为 .
生活中哪类问题可以利用三角函数模型解决?利用三角函数解决实际问题的一般步骤是怎样的?你能够将本节课所学内容画出一个知识结构图吗?其中涉及到哪些数学思想?通过本节课的学习,你还有哪些收获?
实际问题
三角函数模型
解决三角函数问题
联系实际解决问题
周期性
收集数据画散点图
观察图形函数拟合
周期性
课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
