5.2解简易方程(预习衔接.培优卷.含解析)2025-2026学年五年级上册数学人教版
文档属性
| 名称 | 5.2解简易方程(预习衔接.培优卷.含解析)2025-2026学年五年级上册数学人教版 |  | |
| 格式 | doc | ||
| 文件大小 | 472.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-19 11:20:22 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
预习衔接.培优卷 解简易方程
1.下面的式子中,( )不是等式。
A.2x﹣3=15 B.x+5.7 C.5×5=25 D.3x+8=29
2.下列各式中,是方程的是( )
A.2x+5 B.8+x=12 C.3+6.5=9.5
3.根据如图所示,可列方程为( )
A.y+2+200=300 B.200y﹣2=300
C.2y+200=300 D.2y=200+300
4.已知x=y,根据等式的性质,下面各式成立的是( )
A.x+1=y﹣1 B.4x=4y C.x÷2=2y
5.根据如图的线段图列出的方程中,错误的是( )
A. B.
C. D.
6.上海“东方明珠”广播电视塔高468米,是一栋普通住房高度的30倍。这栋普通住房高多少米?设这栋普通住房高x米,下列方程错误的是( )
A.30x=468 B.x÷30=468 C.468÷x=30
7.高速列车的速度是300千米/时,如果速度减少80千米/时,就相当于一辆轿车速度的2倍。要知道轿车的速度,可以用下面的方程( )求解。
A.2x+80=300 B.x+80=300+2
C.2x﹣80=300 D.2x+80=300+2
8.根据“40比a的5倍少2”列出的方程是( )
A.40﹣5a=2 B.5a﹣40=2 C.5a+2=40 D.40﹣2=5a
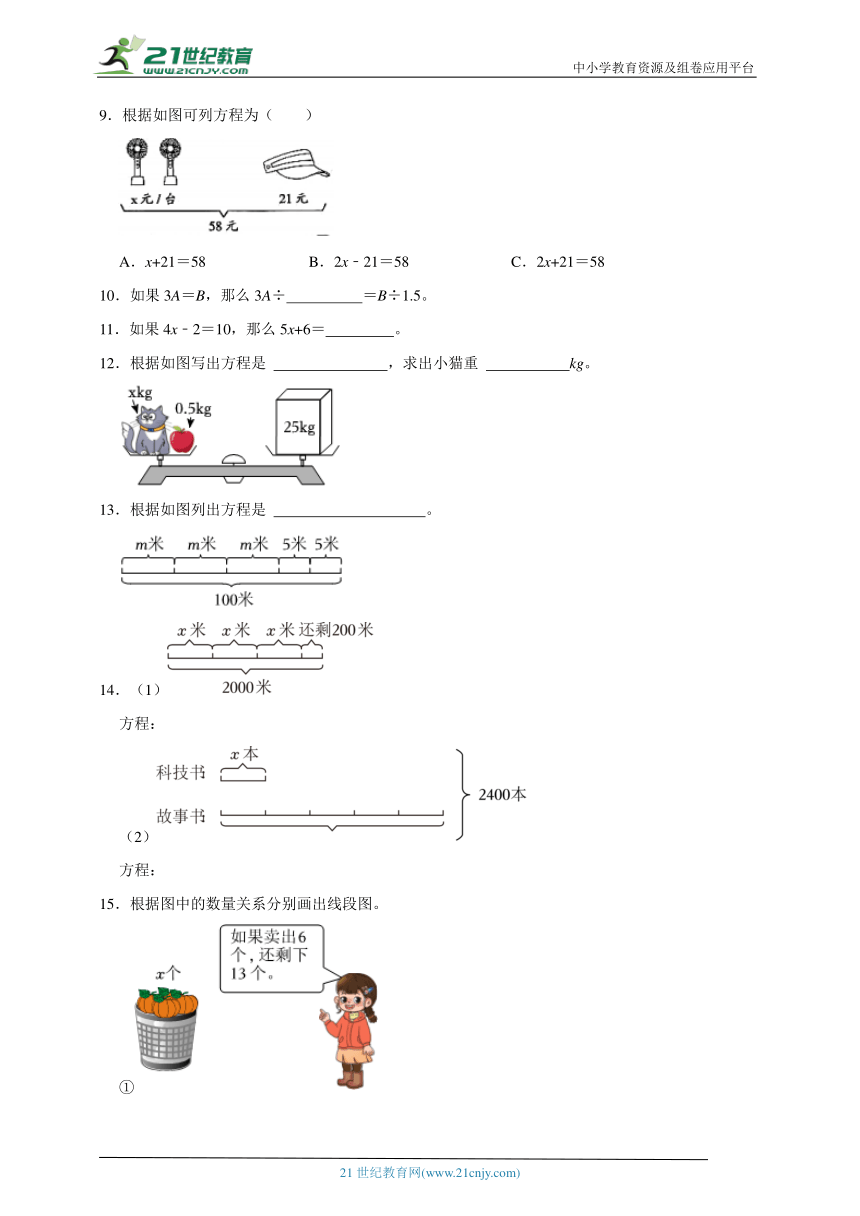
9.根据如图可列方程为( )
A.x+21=58 B.2x﹣21=58 C.2x+21=58
10.如果3A=B,那么3A÷ =B÷1.5。
11.如果4x﹣2=10,那么5x+6= 。
12.根据如图写出方程是 ,求出小猫重 kg。
13.根据如图列出方程是 。
14.(1)
方程:
(2)
方程:
15.根据图中的数量关系分别画出线段图。
①
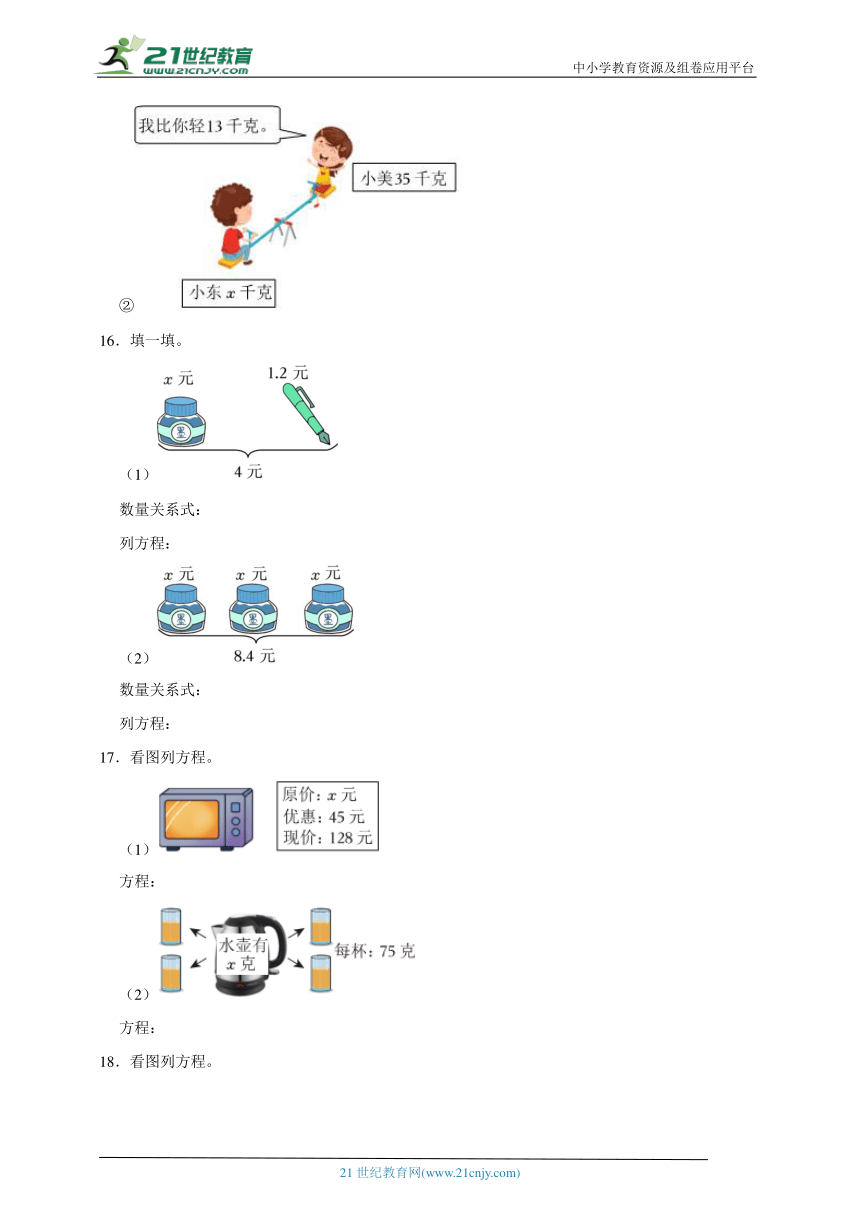
②
16.填一填。
(1)
数量关系式:
列方程:
(2)
数量关系式:
列方程:
17.看图列方程。
(1)
方程:
(2)
方程:
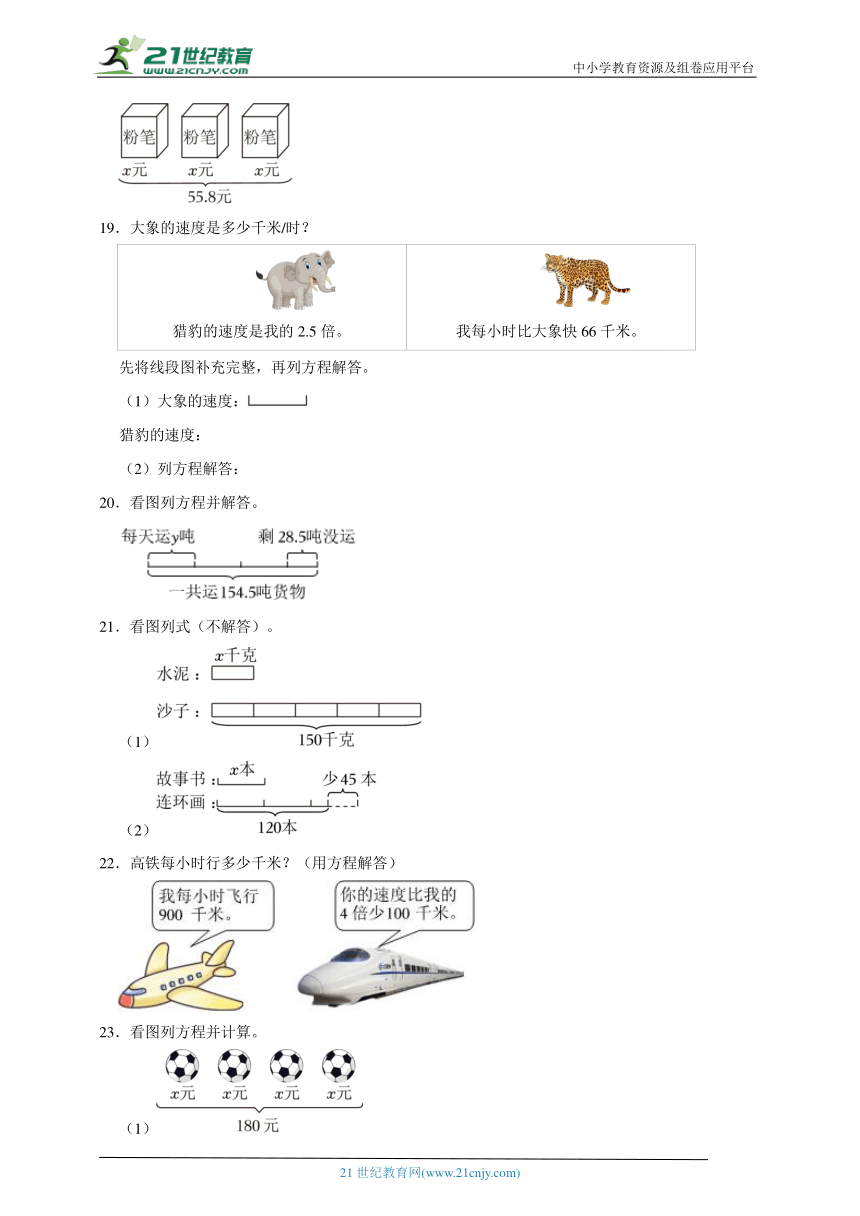
18.看图列方程。
19.大象的速度是多少千米/时?
猎豹的速度是我的2.5倍。 我每小时比大象快66千米。
先将线段图补充完整,再列方程解答。
(1)大象的速度:
猎豹的速度:
(2)列方程解答:
20.看图列方程并解答。
21.看图列式(不解答)。
(1)
(2)
22.高铁每小时行多少千米?(用方程解答)
23.看图列方程并计算。
(1)
(2)
预习衔接.培优卷 解简易方程
参考答案与试题解析
1.下面的式子中,( )不是等式。
A.2x﹣3=15 B.x+5.7 C.5×5=25 D.3x+8=29
【考点】等式的意义.
【答案】B
【分析】表示相等关系的式子叫作等式,由此进行选择。
【解答】解:A、2x﹣3=15,是等式。
B、x+5.7,只是含有未知数的式子,不是等式。
C、5×5=25,是等式。
D、3x+8=29,是等式。
故选:B。
【点评】此题考查了等式的意义及辨析。
2.下列各式中,是方程的是( )
A.2x+5 B.8+x=12 C.3+6.5=9.5
【考点】方程的意义.
【答案】B
【分析】方程是指含有未知数的等式.所以方程必须具备两个条件:①含有未知数;②等式.由此进行选择.
【解答】解:A、2x+5,虽然含未知数,但不是等式,所以不是方程;
B、8+x=12,是含有未知数的等式,是方程;
C、3+6.5=9.5,虽然是等式,但不含有未知数,所以不是方程;
故选:B.
【点评】此题考查方程的辨识:只有含有未知数的等式才是方程.
3.根据如图所示,可列方程为( )
A.y+2+200=300 B.200y﹣2=300
C.2y+200=300 D.2y=200+300
【考点】列方程解应用题(两步需要逆思考).
【答案】C
【分析】观察发现:天平平衡,说明左右两边的质量相等,据此确定数量关系并判断哪个方程正确。
【解答】解:天平左边为(y+y+200)g,右边为300g。
A、左边y+2+200与y+y+200相比,不符合题意。
B、左边200y﹣2与y+y+200相比,不符合题意。
C、左边2y+20与y+y+200相比,符合题意。
D、左边2y与y+y+200相比;右边200+300与300相比,不符合题意。
故选:C。
【点评】本题考查了对天平原理,即等式的基本性质的理解与应用。解答本题时一定要清楚的数量关系是:2个y克的砝码+梨的质量(200克)=菠萝的质量(300克)。
4.已知x=y,根据等式的性质,下面各式成立的是( )
A.x+1=y﹣1 B.4x=4y C.x÷2=2y
【考点】等式的性质.
【答案】B
【分析】等式的性质:性质1、等式两边加同一个数(或式子)结果仍得等式;性质2、等式两边乘同一个数或除以一个不为零的数,结果仍得等式,由此即可判断。
【解答】解:A、由x=y,得到x+1=y+1,故本项不符合题意;
B、由x=y,得到4x=4y,故本项符合题意;
C、由x=y,得到x÷2=y÷2或2x=2y,故本项不符合题意。
故选:B。
【点评】本题考查等式的性质,关键是掌握等式的性质。
5.根据如图的线段图列出的方程中,错误的是( )
A. B.
C. D.
【考点】列方程解应用题(两步需要逆思考).
【答案】B
【分析】观察线段图可知:兔子的只数﹣兔子的只数×=鸡的只数,设兔子有x只,据此列方程解答。
【解答】解:设兔子有x只。
x﹣x=98
(1﹣)x=98
x=98
x=112
答:兔子有112只。
所以错误的是x+x=98。
故选:B。
【点评】此题主要考查了列方程解应用题,弄清题意,找出合适的等量关系,进而列出方程是解答此类问题的关键。
6.上海“东方明珠”广播电视塔高468米,是一栋普通住房高度的30倍。这栋普通住房高多少米?设这栋普通住房高x米,下列方程错误的是( )
A.30x=468 B.x÷30=468 C.468÷x=30
【考点】列方程解应用题(两步需要逆思考).
【答案】B
【分析】根题意可列等量关系式:上海“东方明珠”广播电视塔÷一栋普通住房高度=30或一栋普通住房高度×30=上海“东方明珠”广播电视塔,据此列方程解答。
【解答】解:方法一:
设这栋普通住房高x米。
468÷x=30
x=15.6
方法二:
设这栋普通住房高x米。
30x=468
x=15.6
答:这栋普通住房高15.6米。
故选:B。
【点评】此题主要考查了列方程解应用题,弄清题意,找出合适的等量关系,即:上海“东方明珠”广播电视塔÷一栋普通住房高度=30或一栋普通住房高度×30=上海“东方明珠”广播电视塔,进而列出方程是解答此类问题的关键。
7.高速列车的速度是300千米/时,如果速度减少80千米/时,就相当于一辆轿车速度的2倍。要知道轿车的速度,可以用下面的方程( )求解。
A.2x+80=300 B.x+80=300+2
C.2x﹣80=300 D.2x+80=300+2
【考点】列方程解应用题(两步需要逆思考).
【答案】A
【分析】根据题意,此题的等量关系是:轿车的速度×2+80千米/小时=300千米/时,据此列方程。
【解答】解:根据上面的分析,要知道轿车的速度,可以用方程2x+80=300求解。
故选:A。
【点评】本题考查列方程解应用题,解题关键是找出题目中的等量关系列方程解答。
8.根据“40比a的5倍少2”列出的方程是( )
A.40﹣5a=2 B.5a﹣40=2 C.5a+2=40 D.40﹣2=5a
【考点】列方程解应用题(两步需要逆思考).
【答案】B
【分析】a的5倍即5a,再减40等于2,据此列方程即可。
【解答】解:根据“40比a的5倍少2”列出的方程是5a﹣40=2。
故选:B。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,列方程解决问题。
9.根据如图可列方程为( )
A.x+21=58 B.2x﹣21=58 C.2x+21=58
【考点】列方程解应用题(两步需要逆思考).
【答案】C
【分析】根据等量关系:风扇的钱数+帽子的钱数=58元,列方程即可。
【解答】解:2x+21=58
2x=37
x=18.5
故选:C。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,列方程解决问题。
10.如果3A=B,那么3A÷ 1.5 =B÷1.5。
【考点】等式的性质.
【答案】1.5。
【分析】等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
【解答】解:如果3A=B,那么3A÷1.5=B÷1.5。
故答案为:1.5。
【点评】本题考查了等式的性质。
11.如果4x﹣2=10,那么5x+6= 21 。
【考点】整数方程求解.
【答案】21。
【分析】首先根据等式的性质,两边同时加上2;然后两边再同时除以4,求出方程4x﹣2=10的解;最后把求出的x的值代入5x+6计算即可。
【解答】解:4x﹣2=10
4x﹣2+2=10+2
4x=12
4x÷4=12÷4
x=3
5x+6
=5×3+6
=15+6
=21
故答案为:21。
【点评】此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去、同时乘或同时除以一个数(0除外),两边仍相等。
12.根据如图写出方程是 x+0.5=25 ,求出小猫重 24.5 kg。
【考点】列方程解应用题(两步需要逆思考).
【答案】x+0.5=25,24.5。
【分析】根据等量关系:小猫的重量+苹果的重量=25kg,列方程解答即可。
【解答】解:x+0.5=25
x+0.5﹣0.5=25﹣0.5
x=24.5
答:方程是x+0.5=25,求出小猫重24.5kg。
故答案为:x+0.5=25,24.5。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,列方程解决问题。
13.根据如图列出方程是 m+m+m+5+5=100 。
【考点】列方程解应用题(两步需要逆思考).
【答案】m+m+m+5+5=100。
【分析】根据等量关系:把每小段的米数相加等于100米,列方程即可。
【解答】解:m+m+m+5+5=100
3m+10=100
3m=90
m=30
答:根据如图列出方程是m+m+m+5+5=100。
故答案为:m+m+m+5+5=100。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,列方程解决问题。
14.(1)
方程: x+x+x+200=2000
(2)
方程: 5x+x=2400
【考点】列方程解应用题(两步需要逆思考).
【答案】(1)x+x+x+200=2000;(2)5x+x=2400。
【分析】(1)观察线段图可知:x+x+x+200=2000,据此解答。
(2)观察线段图可知:故事书是科技书的5倍,设科技书有x本,则故事书有5x本,根据科技书的数量+故事书的数量=2400,列方程解答。
【解答】解:(1)x+x+x+200=2000
3x=1800
x=600
答:x的值是600。
(2)5x+x=2400
6x=2400
x=400
答:科技书有400本。
故答案为:x+x+x+200=2000;5x+x=2400。
【点评】此题主要考查了列方程解应用题,弄清题意,找出合适的等量关系,进而列出方程是解答此类问题的关键。
15.根据图中的数量关系分别画出线段图。
①
②
【考点】列方程解应用题(两步需要逆思考).
【答案】①(答案不唯一)
②(答案不唯一)
【分析】①卖出的个数+剩下的个数=总个数,所以数量关系是:13+6=x;
②小美的体重+13=小东的体重,所以数量关系是:13+35=x。
【解答】解:①数量关系是:13+6=x
(答案不唯一)
②数量关系是:13+35=x
(答案不唯一)
【点评】本题考查的主要内容是用方程表示数量关系问题。
16.填一填。
(1)
数量关系式: 1瓶墨水的钱数+1支钢笔的钱数=4元
列方程: x+1.2=4
(2)
数量关系式: 1瓶墨水的钱数×3=8.4元
列方程: 3x=8.4
【考点】列方程解应用题(两步需要逆思考).
【答案】(1)1瓶墨水的钱数+1支钢笔的钱数=4元,x+1.2=4;(2)1瓶墨水的钱数×3=8.4元,3x=8.4。
【分析】(1)1瓶墨水的钱数与1支钢笔的钱数和等于4元,据此写出等量关系并列方程解答即可;
(2)3瓶墨水共8.4元,据此写出等量关系并列方程解答即可。
【解答】解:(1)数量关系式:1瓶墨水的钱数+1支钢笔的钱数=4元
x+1.2=4
x+1.2﹣1.2=4﹣1.2
x=2.8
答:一瓶墨水2.8元。
(2)数量关系式:1瓶墨水的钱数×3=8.4元
3x=8.4
3x÷3=8.4÷3
x=2.8
答:每瓶墨水2.8元。
故答案为:1瓶墨水的钱数+1支钢笔的钱数=4元,x+1.2=4;1瓶墨水的钱数×3=8.4元,3x=8.4。
【点评】利用方程解决问题的关键是准确分析题目中的等量关系。
17.看图列方程。
(1)
方程: x﹣45=128
(2)
方程: x÷4=75
【考点】列方程解应用题(两步需要逆思考).
【答案】(1)x﹣45=128;
(2)x÷4=75。
【分析】(1)根据题意可知,原价﹣优惠的部分=现价,据此列方程解答。
(2)这壶水的质量÷4=75克,据此列方程解答。
【解答】解:(1)x﹣45=128
x﹣45+45=128+45
x=173
答:原价173元。
(2)x÷4=75
x÷4×4=75×4
x=300
答:这壶水的质量是300克。
故答案为:x﹣45=128;x÷4=75。
【点评】此题考查的目的是理解掌握列方程解决问题的方法及应用,关键是找出等量关系。
18.看图列方程。
【考点】列方程解应用题(两步需要逆思考).
【答案】x+x+x=55.8。
【分析】根据等量关系:每盒粉笔的钱数和为55.8元,列方程解答即可。
【解答】解:x+x+x=55.8
3x=55.8
x=18.6
答:每盒粉笔18.6元。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题。
19.大象的速度是多少千米/时?
猎豹的速度是我的2.5倍。 我每小时比大象快66千米。
先将线段图补充完整,再列方程解答。
(1)大象的速度:
猎豹的速度:
(2)列方程解答:
【考点】列方程解应用题(两步需要逆思考).
【答案】(1);(2)44千米/时。
【分析】(1)根据猎豹的速度是大象的2.5倍解答即可。
(2)设大象的速度是x千米/时,根据等量关系:大象的速度×2.5=猎豹的速度,列方程解答即可。
【解答】解:(1)大象的速度:
猎豹的速度:
(2)设大象的速度是x千米/时。
2.5x=x+66
1.5x=66
x=44
答:大象的速度是44千米/时。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题。
20.看图列方程并解答。
【考点】列方程解应用题(两步需要逆思考).
【答案】42吨。
【分析】根据等量关系:每天运的吨数×运的天数+剩下的吨数=一共运的吨数,列方程解答即可。
【解答】解:3y+28.5=154.5
3y=126
y=42
答:每天运42吨。
【点评】本题主要考查了列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题。
21.看图列式(不解答)。
(1)
(2)
【考点】列方程解应用题(两步需要逆思考).
【答案】(1)5x=150;(2)3x﹣45=120。
【分析】(1)根据等量关系:水泥的质量×5=沙子的质量,列方程解答即可;
(2)根据等量关系:故事书的本数×3﹣45本=连环画的本数,列方程解答即可。
【解答】解:(1)5x=150
5x÷5=150÷5
x=30
答:水泥30千克。
(2)3x﹣45=120
3x=165
x=55
答:故事书55本。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,列方程解决问题。
22.高铁每小时行多少千米?(用方程解答)
【考点】列方程解应用题(两步需要逆思考).
【答案】250千米。
【分析】设高铁每小时行x千米,根据等量关系:高铁得速度×4﹣100千米=飞机得速度,列方程解答即可。
【解答】解:设高铁每小时行x千米。
4x﹣100=900
4x=1000
x=250
答:高铁每小时行250千米。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题。
23.看图列方程并计算。
(1)
(2)
【考点】列方程解应用题(两步需要逆思考).
【答案】(1)45元;(2)5cm。
【分析】(1)根据等量关系:足球的单价×足球的个数=180元,列方程解答即可。
(2)根据等量关系:腰+腰+底边=14cm,列方程解答即可。
【解答】解:(1)4x=180
4x÷4=180÷4
x=45
答:足球的单价为45元。
(2)2x+4=14
2x=10
x=5
答:x为5cm。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,列方程解决问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
预习衔接.培优卷 解简易方程
1.下面的式子中,( )不是等式。
A.2x﹣3=15 B.x+5.7 C.5×5=25 D.3x+8=29
2.下列各式中,是方程的是( )
A.2x+5 B.8+x=12 C.3+6.5=9.5
3.根据如图所示,可列方程为( )
A.y+2+200=300 B.200y﹣2=300
C.2y+200=300 D.2y=200+300
4.已知x=y,根据等式的性质,下面各式成立的是( )
A.x+1=y﹣1 B.4x=4y C.x÷2=2y
5.根据如图的线段图列出的方程中,错误的是( )
A. B.
C. D.
6.上海“东方明珠”广播电视塔高468米,是一栋普通住房高度的30倍。这栋普通住房高多少米?设这栋普通住房高x米,下列方程错误的是( )
A.30x=468 B.x÷30=468 C.468÷x=30
7.高速列车的速度是300千米/时,如果速度减少80千米/时,就相当于一辆轿车速度的2倍。要知道轿车的速度,可以用下面的方程( )求解。
A.2x+80=300 B.x+80=300+2
C.2x﹣80=300 D.2x+80=300+2
8.根据“40比a的5倍少2”列出的方程是( )
A.40﹣5a=2 B.5a﹣40=2 C.5a+2=40 D.40﹣2=5a
9.根据如图可列方程为( )
A.x+21=58 B.2x﹣21=58 C.2x+21=58
10.如果3A=B,那么3A÷ =B÷1.5。
11.如果4x﹣2=10,那么5x+6= 。
12.根据如图写出方程是 ,求出小猫重 kg。
13.根据如图列出方程是 。
14.(1)
方程:
(2)
方程:
15.根据图中的数量关系分别画出线段图。
①
②
16.填一填。
(1)
数量关系式:
列方程:
(2)
数量关系式:
列方程:
17.看图列方程。
(1)
方程:
(2)
方程:
18.看图列方程。
19.大象的速度是多少千米/时?
猎豹的速度是我的2.5倍。 我每小时比大象快66千米。
先将线段图补充完整,再列方程解答。
(1)大象的速度:
猎豹的速度:
(2)列方程解答:
20.看图列方程并解答。
21.看图列式(不解答)。
(1)
(2)
22.高铁每小时行多少千米?(用方程解答)
23.看图列方程并计算。
(1)
(2)
预习衔接.培优卷 解简易方程
参考答案与试题解析
1.下面的式子中,( )不是等式。
A.2x﹣3=15 B.x+5.7 C.5×5=25 D.3x+8=29
【考点】等式的意义.
【答案】B
【分析】表示相等关系的式子叫作等式,由此进行选择。
【解答】解:A、2x﹣3=15,是等式。
B、x+5.7,只是含有未知数的式子,不是等式。
C、5×5=25,是等式。
D、3x+8=29,是等式。
故选:B。
【点评】此题考查了等式的意义及辨析。
2.下列各式中,是方程的是( )
A.2x+5 B.8+x=12 C.3+6.5=9.5
【考点】方程的意义.
【答案】B
【分析】方程是指含有未知数的等式.所以方程必须具备两个条件:①含有未知数;②等式.由此进行选择.
【解答】解:A、2x+5,虽然含未知数,但不是等式,所以不是方程;
B、8+x=12,是含有未知数的等式,是方程;
C、3+6.5=9.5,虽然是等式,但不含有未知数,所以不是方程;
故选:B.
【点评】此题考查方程的辨识:只有含有未知数的等式才是方程.
3.根据如图所示,可列方程为( )
A.y+2+200=300 B.200y﹣2=300
C.2y+200=300 D.2y=200+300
【考点】列方程解应用题(两步需要逆思考).
【答案】C
【分析】观察发现:天平平衡,说明左右两边的质量相等,据此确定数量关系并判断哪个方程正确。
【解答】解:天平左边为(y+y+200)g,右边为300g。
A、左边y+2+200与y+y+200相比,不符合题意。
B、左边200y﹣2与y+y+200相比,不符合题意。
C、左边2y+20与y+y+200相比,符合题意。
D、左边2y与y+y+200相比;右边200+300与300相比,不符合题意。
故选:C。
【点评】本题考查了对天平原理,即等式的基本性质的理解与应用。解答本题时一定要清楚的数量关系是:2个y克的砝码+梨的质量(200克)=菠萝的质量(300克)。
4.已知x=y,根据等式的性质,下面各式成立的是( )
A.x+1=y﹣1 B.4x=4y C.x÷2=2y
【考点】等式的性质.
【答案】B
【分析】等式的性质:性质1、等式两边加同一个数(或式子)结果仍得等式;性质2、等式两边乘同一个数或除以一个不为零的数,结果仍得等式,由此即可判断。
【解答】解:A、由x=y,得到x+1=y+1,故本项不符合题意;
B、由x=y,得到4x=4y,故本项符合题意;
C、由x=y,得到x÷2=y÷2或2x=2y,故本项不符合题意。
故选:B。
【点评】本题考查等式的性质,关键是掌握等式的性质。
5.根据如图的线段图列出的方程中,错误的是( )
A. B.
C. D.
【考点】列方程解应用题(两步需要逆思考).
【答案】B
【分析】观察线段图可知:兔子的只数﹣兔子的只数×=鸡的只数,设兔子有x只,据此列方程解答。
【解答】解:设兔子有x只。
x﹣x=98
(1﹣)x=98
x=98
x=112
答:兔子有112只。
所以错误的是x+x=98。
故选:B。
【点评】此题主要考查了列方程解应用题,弄清题意,找出合适的等量关系,进而列出方程是解答此类问题的关键。
6.上海“东方明珠”广播电视塔高468米,是一栋普通住房高度的30倍。这栋普通住房高多少米?设这栋普通住房高x米,下列方程错误的是( )
A.30x=468 B.x÷30=468 C.468÷x=30
【考点】列方程解应用题(两步需要逆思考).
【答案】B
【分析】根题意可列等量关系式:上海“东方明珠”广播电视塔÷一栋普通住房高度=30或一栋普通住房高度×30=上海“东方明珠”广播电视塔,据此列方程解答。
【解答】解:方法一:
设这栋普通住房高x米。
468÷x=30
x=15.6
方法二:
设这栋普通住房高x米。
30x=468
x=15.6
答:这栋普通住房高15.6米。
故选:B。
【点评】此题主要考查了列方程解应用题,弄清题意,找出合适的等量关系,即:上海“东方明珠”广播电视塔÷一栋普通住房高度=30或一栋普通住房高度×30=上海“东方明珠”广播电视塔,进而列出方程是解答此类问题的关键。
7.高速列车的速度是300千米/时,如果速度减少80千米/时,就相当于一辆轿车速度的2倍。要知道轿车的速度,可以用下面的方程( )求解。
A.2x+80=300 B.x+80=300+2
C.2x﹣80=300 D.2x+80=300+2
【考点】列方程解应用题(两步需要逆思考).
【答案】A
【分析】根据题意,此题的等量关系是:轿车的速度×2+80千米/小时=300千米/时,据此列方程。
【解答】解:根据上面的分析,要知道轿车的速度,可以用方程2x+80=300求解。
故选:A。
【点评】本题考查列方程解应用题,解题关键是找出题目中的等量关系列方程解答。
8.根据“40比a的5倍少2”列出的方程是( )
A.40﹣5a=2 B.5a﹣40=2 C.5a+2=40 D.40﹣2=5a
【考点】列方程解应用题(两步需要逆思考).
【答案】B
【分析】a的5倍即5a,再减40等于2,据此列方程即可。
【解答】解:根据“40比a的5倍少2”列出的方程是5a﹣40=2。
故选:B。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,列方程解决问题。
9.根据如图可列方程为( )
A.x+21=58 B.2x﹣21=58 C.2x+21=58
【考点】列方程解应用题(两步需要逆思考).
【答案】C
【分析】根据等量关系:风扇的钱数+帽子的钱数=58元,列方程即可。
【解答】解:2x+21=58
2x=37
x=18.5
故选:C。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,列方程解决问题。
10.如果3A=B,那么3A÷ 1.5 =B÷1.5。
【考点】等式的性质.
【答案】1.5。
【分析】等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等。
【解答】解:如果3A=B,那么3A÷1.5=B÷1.5。
故答案为:1.5。
【点评】本题考查了等式的性质。
11.如果4x﹣2=10,那么5x+6= 21 。
【考点】整数方程求解.
【答案】21。
【分析】首先根据等式的性质,两边同时加上2;然后两边再同时除以4,求出方程4x﹣2=10的解;最后把求出的x的值代入5x+6计算即可。
【解答】解:4x﹣2=10
4x﹣2+2=10+2
4x=12
4x÷4=12÷4
x=3
5x+6
=5×3+6
=15+6
=21
故答案为:21。
【点评】此题主要考查了根据等式的性质解方程的能力,即等式两边同时加上或同时减去、同时乘或同时除以一个数(0除外),两边仍相等。
12.根据如图写出方程是 x+0.5=25 ,求出小猫重 24.5 kg。
【考点】列方程解应用题(两步需要逆思考).
【答案】x+0.5=25,24.5。
【分析】根据等量关系:小猫的重量+苹果的重量=25kg,列方程解答即可。
【解答】解:x+0.5=25
x+0.5﹣0.5=25﹣0.5
x=24.5
答:方程是x+0.5=25,求出小猫重24.5kg。
故答案为:x+0.5=25,24.5。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,列方程解决问题。
13.根据如图列出方程是 m+m+m+5+5=100 。
【考点】列方程解应用题(两步需要逆思考).
【答案】m+m+m+5+5=100。
【分析】根据等量关系:把每小段的米数相加等于100米,列方程即可。
【解答】解:m+m+m+5+5=100
3m+10=100
3m=90
m=30
答:根据如图列出方程是m+m+m+5+5=100。
故答案为:m+m+m+5+5=100。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,列方程解决问题。
14.(1)
方程: x+x+x+200=2000
(2)
方程: 5x+x=2400
【考点】列方程解应用题(两步需要逆思考).
【答案】(1)x+x+x+200=2000;(2)5x+x=2400。
【分析】(1)观察线段图可知:x+x+x+200=2000,据此解答。
(2)观察线段图可知:故事书是科技书的5倍,设科技书有x本,则故事书有5x本,根据科技书的数量+故事书的数量=2400,列方程解答。
【解答】解:(1)x+x+x+200=2000
3x=1800
x=600
答:x的值是600。
(2)5x+x=2400
6x=2400
x=400
答:科技书有400本。
故答案为:x+x+x+200=2000;5x+x=2400。
【点评】此题主要考查了列方程解应用题,弄清题意,找出合适的等量关系,进而列出方程是解答此类问题的关键。
15.根据图中的数量关系分别画出线段图。
①
②
【考点】列方程解应用题(两步需要逆思考).
【答案】①(答案不唯一)
②(答案不唯一)
【分析】①卖出的个数+剩下的个数=总个数,所以数量关系是:13+6=x;
②小美的体重+13=小东的体重,所以数量关系是:13+35=x。
【解答】解:①数量关系是:13+6=x
(答案不唯一)
②数量关系是:13+35=x
(答案不唯一)
【点评】本题考查的主要内容是用方程表示数量关系问题。
16.填一填。
(1)
数量关系式: 1瓶墨水的钱数+1支钢笔的钱数=4元
列方程: x+1.2=4
(2)
数量关系式: 1瓶墨水的钱数×3=8.4元
列方程: 3x=8.4
【考点】列方程解应用题(两步需要逆思考).
【答案】(1)1瓶墨水的钱数+1支钢笔的钱数=4元,x+1.2=4;(2)1瓶墨水的钱数×3=8.4元,3x=8.4。
【分析】(1)1瓶墨水的钱数与1支钢笔的钱数和等于4元,据此写出等量关系并列方程解答即可;
(2)3瓶墨水共8.4元,据此写出等量关系并列方程解答即可。
【解答】解:(1)数量关系式:1瓶墨水的钱数+1支钢笔的钱数=4元
x+1.2=4
x+1.2﹣1.2=4﹣1.2
x=2.8
答:一瓶墨水2.8元。
(2)数量关系式:1瓶墨水的钱数×3=8.4元
3x=8.4
3x÷3=8.4÷3
x=2.8
答:每瓶墨水2.8元。
故答案为:1瓶墨水的钱数+1支钢笔的钱数=4元,x+1.2=4;1瓶墨水的钱数×3=8.4元,3x=8.4。
【点评】利用方程解决问题的关键是准确分析题目中的等量关系。
17.看图列方程。
(1)
方程: x﹣45=128
(2)
方程: x÷4=75
【考点】列方程解应用题(两步需要逆思考).
【答案】(1)x﹣45=128;
(2)x÷4=75。
【分析】(1)根据题意可知,原价﹣优惠的部分=现价,据此列方程解答。
(2)这壶水的质量÷4=75克,据此列方程解答。
【解答】解:(1)x﹣45=128
x﹣45+45=128+45
x=173
答:原价173元。
(2)x÷4=75
x÷4×4=75×4
x=300
答:这壶水的质量是300克。
故答案为:x﹣45=128;x÷4=75。
【点评】此题考查的目的是理解掌握列方程解决问题的方法及应用,关键是找出等量关系。
18.看图列方程。
【考点】列方程解应用题(两步需要逆思考).
【答案】x+x+x=55.8。
【分析】根据等量关系:每盒粉笔的钱数和为55.8元,列方程解答即可。
【解答】解:x+x+x=55.8
3x=55.8
x=18.6
答:每盒粉笔18.6元。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题。
19.大象的速度是多少千米/时?
猎豹的速度是我的2.5倍。 我每小时比大象快66千米。
先将线段图补充完整,再列方程解答。
(1)大象的速度:
猎豹的速度:
(2)列方程解答:
【考点】列方程解应用题(两步需要逆思考).
【答案】(1);(2)44千米/时。
【分析】(1)根据猎豹的速度是大象的2.5倍解答即可。
(2)设大象的速度是x千米/时,根据等量关系:大象的速度×2.5=猎豹的速度,列方程解答即可。
【解答】解:(1)大象的速度:
猎豹的速度:
(2)设大象的速度是x千米/时。
2.5x=x+66
1.5x=66
x=44
答:大象的速度是44千米/时。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题。
20.看图列方程并解答。
【考点】列方程解应用题(两步需要逆思考).
【答案】42吨。
【分析】根据等量关系:每天运的吨数×运的天数+剩下的吨数=一共运的吨数,列方程解答即可。
【解答】解:3y+28.5=154.5
3y=126
y=42
答:每天运42吨。
【点评】本题主要考查了列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题。
21.看图列式(不解答)。
(1)
(2)
【考点】列方程解应用题(两步需要逆思考).
【答案】(1)5x=150;(2)3x﹣45=120。
【分析】(1)根据等量关系:水泥的质量×5=沙子的质量,列方程解答即可;
(2)根据等量关系:故事书的本数×3﹣45本=连环画的本数,列方程解答即可。
【解答】解:(1)5x=150
5x÷5=150÷5
x=30
答:水泥30千克。
(2)3x﹣45=120
3x=165
x=55
答:故事书55本。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,列方程解决问题。
22.高铁每小时行多少千米?(用方程解答)
【考点】列方程解应用题(两步需要逆思考).
【答案】250千米。
【分析】设高铁每小时行x千米,根据等量关系:高铁得速度×4﹣100千米=飞机得速度,列方程解答即可。
【解答】解:设高铁每小时行x千米。
4x﹣100=900
4x=1000
x=250
答:高铁每小时行250千米。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,设未知数为x,由此列方程解决问题。
23.看图列方程并计算。
(1)
(2)
【考点】列方程解应用题(两步需要逆思考).
【答案】(1)45元;(2)5cm。
【分析】(1)根据等量关系:足球的单价×足球的个数=180元,列方程解答即可。
(2)根据等量关系:腰+腰+底边=14cm,列方程解答即可。
【解答】解:(1)4x=180
4x÷4=180÷4
x=45
答:足球的单价为45元。
(2)2x+4=14
2x=10
x=5
答:x为5cm。
【点评】此题考查列方程解应用题,关键是根据题意找出基本数量关系,列方程解决问题。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
