冀教版九年级上册23.1 平均数与加权平均数(第2课时 加权平均数) 教案(表格式)
文档属性
| 名称 | 冀教版九年级上册23.1 平均数与加权平均数(第2课时 加权平均数) 教案(表格式) |
|
|
| 格式 | docx | ||
| 文件大小 | 399.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-20 00:00:00 | ||
图片预览





文档简介
23.1 平均数与加权平均数
课题 第2课时 加权平均数 授课类型 新授课
授课人
教学内容 课本P6-11
教学目标 1.理解加权平均数的意义,了解“权”的含义. 2.明确加权平均数与算术平均数的关系,掌握加权平均数的计算方法. 3.在实际问题情境中理解加权平均数的意义,体会数学与生活之间的密切联系.
教学重难点 重点:掌握加权平均数的计算方法. 难点:理解数据的权和加权平均数的概念.
教学准备 多媒体课件
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 想一想:一家公司打算招聘一名英文翻译. 对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们的各项成绩(百分制)如下表所示. 如果这家公司想招一名综合能力较强的翻译,计算两名应试者的平均成绩(百分制),从他们的成绩看,应该录取谁? 预设答案:根据平均数公式, 甲的平均成绩为 5, 乙的平均成绩为 因为甲的平均成绩比乙高,所以应该录取甲. 师生活动:学生思考后小组合作交流,小组代表发言,教师展示解法,导出新课. 通过复习求算术平均数,做好新旧知识的衔接,以贴近学生实际生活的实例导入新课,为本节课的学习做好铺垫.
2.实践探究,学习新知 1.加权平均数的概念 【观察与思考】 问题1 假期里,小红和小惠结伴去买菜,三次购买的西红柿价格和数量如下表: 从平均价格来看,谁买的西红柿要便宜一些? 思考小亮和小明的下列说法,你认为他俩谁说得对?为什么? 预设答案:小红购买不同单价的西红柿的数量不同,所以平均价格不是三个单价的平均数.实际上,平均价格是总花费金额与购买总量的比. 所以: 从平均价格看,小红买的西红柿要便宜些. 师生活动:小组内合作交流,判断两个人的说法谁正确,教师对学生的回答进行点评,并引导学生通过计算平均数比较谁买的西红柿更便宜,学生独立完成计算平均数的过程,教师点评. 【归纳概念】 已知n个数,…,,若,…,为一组正数,则把 叫做n个数,…,的加权平均数,w1,w2,…,wn分别叫做这n个数的权重,简称为权. 教师提问: (1)在“共同探究”中,加权平均数是多少 哪些数是权 预设答案:小红购买的西红柿平均价格约为2.67元/千克,它是数4,3,2的加权平均数,三个数的权分别为1,2,3。 你能举出用加权平均数计算平均数的生活实例吗 师生活动:学生小组合作交流,创设不同的求平均数的生活情境,小组代表展示问题后,其他学生完成解答,教师进行点评,以鼓励学生参与为主. 【例题】 例1 某学校为了鼓励学生积极参加体育锻炼,规定体育科目学期成绩满分为100分,其中平时表现(早操、课外体育活动)、期中考试和期末考试成绩按比例3∶2∶5计入学期总成绩.甲、乙两名同学的各项成绩如下: 学生平时表现/分期中考试/分期末考试/分甲959085乙809588
分别计算甲、乙的学期总成绩. 解:三项成绩按3∶2∶5的比例确定,就是分别用3,2,5作为三项成绩的权,用加权平均数作为学期总成绩. 甲的学期总成绩为=89(分), 乙的学期总成绩为=87(分). 思考: (1)分配的“权”不同,甲、乙二人的总成绩是否会发生变化 回答:分配的“权”不同,甲、乙二人的总成绩会发生变化. (2)算术平均数和加权平均数的区别和联系是什么 回答:算术平均数是加权平均数的一种特殊情况(它特殊在各项的权相等);在实际问题中,各项权不相等时,计算平均数时就要采用加权平均数. 做一做 某电视节目主持人大赛要进行专业素质、综合素质、外语水平和临场应变能力四项测试,各项测试均采用10分制,两名选手的各项测试成绩如下表所示: 测试项目专业 素质综合 素质外语 水平临场应 变能力测试成 绩/分甲9.08.57.58.8乙8.09.28.49.0
(1)如果按四项测试成绩的算术平均数排名次,名次是怎样的 (2)如果规定按专业素质、综合素质、外语水平和临场应变能力四项测试的成绩各占60%,20%,10%,10%计算总成绩,名次有什么变化 解:(1)甲、乙各项成绩的算术平均数分别为: =8.45(分), =8.65(分). 比较算术平均数,乙排名第一,甲排名第二. (2)甲、乙的加权平均成绩分别为: =9.0×60%+8.5×20%+7.5×10%+8.8×10%=8.73(分), =8.0×60%+9.2×20%+8.4×10%+9.0×10%=8.38(分). 比较加权平均数,甲排名第一,乙排名第二. 【归纳总结】 比较加权平均数,甲排名第一,乙排名第二. 总结:权主要有三种表现形式:百分比,比例,数据出现的次数. 老师带领总结加权平均数的意义 加权平均数不仅与每个数据的大小有关,还受每个数据的权的影响. 数据的“权”反映数据的“重要程度”. 权越大,该数据所占的比重越大;反之,权越小,该数据所占的比重越小. 注意:(1)一组数据的平均数是唯一的. (2)平均数的单位要与原数据的单位一致. 2.估测数据的平均数 目测教室黑板的宽度,然后汇总,计算出全班同学估测数据的平均数,并实际测量,比较各小组的平均数波动情况和全班同学平均数与测量结果的误差. 师生活动:学生以小组为单位,先进行目测,并计算出结果,然后全班汇总,教师重在组织并引导学生观察. 例2 从某校九年级男生中,任意选出100人,分别测量他们的体重,将数据进行分组整理,结果如下表: 计算这100名男生的平均体重. 解:五组数据的组中值分别为47,53,59,65,71.加权平均数为 所以,这100名男生的平均体重约为59.6kg. 师生活动:学生独立完成后,小组内交流答案,小组代表板书解答过程,教师在巡视过程中帮助有困难的学生,对学生的展示进行点评. 通过解决生活实际问题,引导学生思考重要性的差异对平均数的影响,为加权平均数概念的形成做好铺垫,在探究过程中,充分发挥学生的主观能动性,让学生积极思考,合作交流,在数学活动中逐步形成概念. 教师设计开放性题目,学生通过合作交流,共同创设问题情境,体会“权”对平均数的影响,加深学生对加权平均数的理解,提高学生的发散性思维,达到学生数学能力的提升. 学会利用加权平均数进行运算,加深对所学知识的理解,提高学生知识的综合运用能力. 巩固所学知识,加深对所学知识的理解,提高学生知识的综合运用能力. 通过实际动手,让学生体会在实际生活中,我们经常要对某个量进行测量,测量时,往往会产生误差,为了得到比较准确的结果,可以进行多次重复的测量,用这些测量值的平均数作为这个量的估计值. 让学生明白加权平均数的权,有时是一组数据的组中值.
3.学以致用,应用新知 考点 加权平均数的计算 练习1 一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示,请确定两人的名次. 解:选手A的最后得分是 选手B的最后得分是 由上可知选手B获得第一名,选手A获得第二名. 变式训练1 某单位定期对员工的专业知识、工作业绩、出勤情况三个方面进行考核(考核的满分均为100分),三个方面的重要性之比为3:5:2.小王经过考核后所得的分数依次为90分、88分、83分,那么小王的最后得分是( ) A. 87 分 B. 87. 5 分 C.87.6 分 D. 88 分 答案:C 练习2 某公交公司为了了解673路公交汽车的运营情况,该公司统计了某天673路公共汽车每个运行班次的载客量,得到下面的图表: 载客量组中值频数(班次)1≤x<2111321≤x<4131541≤x<61a2061≤x<81712281≤x<1019118101≤x(1)写出a,b的值; (2)如果673路公共汽车的平均每班载客量超过80人,公司就要考虑增加这一线路运行的车辆数,请你判断是否需要增加这一线路的车辆数. 解:(1) (2)673路公共汽车平均每班的载客量为: ∴不需要增加这一线路的车辆数. 变式训练2 对一组数据进行了整理,结果如下表: 则这组数据的平均数约是( ) A.10 B.11 C.12 D.16 答案:B 巩固所学知识,加深对所学知识的理解,提高学生知识的综合运用能力. 巩固“权”是一组数据的组中值,加深对所学知识的理解,提高学生知识的综合运用能力.
4.随堂训练,巩固新知 1.某超市销售A , B , C , D四种矿泉水,它们的单价依次是5元、3元、2元、1元.某天的销售情况如图所示,则这天销售的矿泉水的平均单价是( ) A.1.95 元 B.2. 15 元 C.2. 25 元 D.2.75 元 答案:C 2.某校拟招聘一批优秀教师,其中某位教师笔试、试讲、面试三轮测试成绩分别为92分、 85分、90分,综合成绩笔试占40%,试讲占40%,面试占20%,则该名教师的综合成绩为______分. 答案:88.8 3.某跳水队为了解运动员的年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个跳水队运动员的平均年龄(结果取整数). 解:这个跳水队运动员的平均年龄为 ≈14(岁). 4.如果某家公司想招一名笔译能力较强的翻译,听、说、读、写的成绩按照2:1:3:4的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁? 解: 因为乙的成绩比甲高,所以应该录取乙. 5.某部队为测量一批新制造的炮弹的杀伤半径,从中抽查了50枚炮弹,它们的杀伤半径(米)如下表所示: 求这批炮弹的平均杀伤半径. 解:由表可得出各组数据的组中值分别是30,50,70,90, ∴这批炮弹的平均杀伤半径大约是60. 8米. 通过本环节的学习,让学生巩固所学知识.
5.课堂小结,自我完善 w1,w2,…,wn分别叫做这n个数的权重,简称为权. 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容.
6.布置作业 课本P8习题A组,P9习题B组,P11习题A组 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 23.1 平均数与加权平均数 第2课时 加权平均数 1.加权平均数 概念: 2.例题讲解 3.随堂练习 4.估测数据的平均数 5.课堂小结 6.作业布置 提纲掣领,重点突出.
教后反思 通过教学,预定的目标已经达到.学生主动参与面广,学习兴趣浓,练习的达成度高,教师得到了解放,学生也得到了一次锻炼的机会,很多学生从自学中找到了自信,转变了自己的学习方式,从过度依赖老师转到了先自学再提问,培养了自己的自学能力与独立思考问题的能力. 反思,更进一步提升.
课题 第2课时 加权平均数 授课类型 新授课
授课人
教学内容 课本P6-11
教学目标 1.理解加权平均数的意义,了解“权”的含义. 2.明确加权平均数与算术平均数的关系,掌握加权平均数的计算方法. 3.在实际问题情境中理解加权平均数的意义,体会数学与生活之间的密切联系.
教学重难点 重点:掌握加权平均数的计算方法. 难点:理解数据的权和加权平均数的概念.
教学准备 多媒体课件
教与学互动设计(教学过程) 设计意图
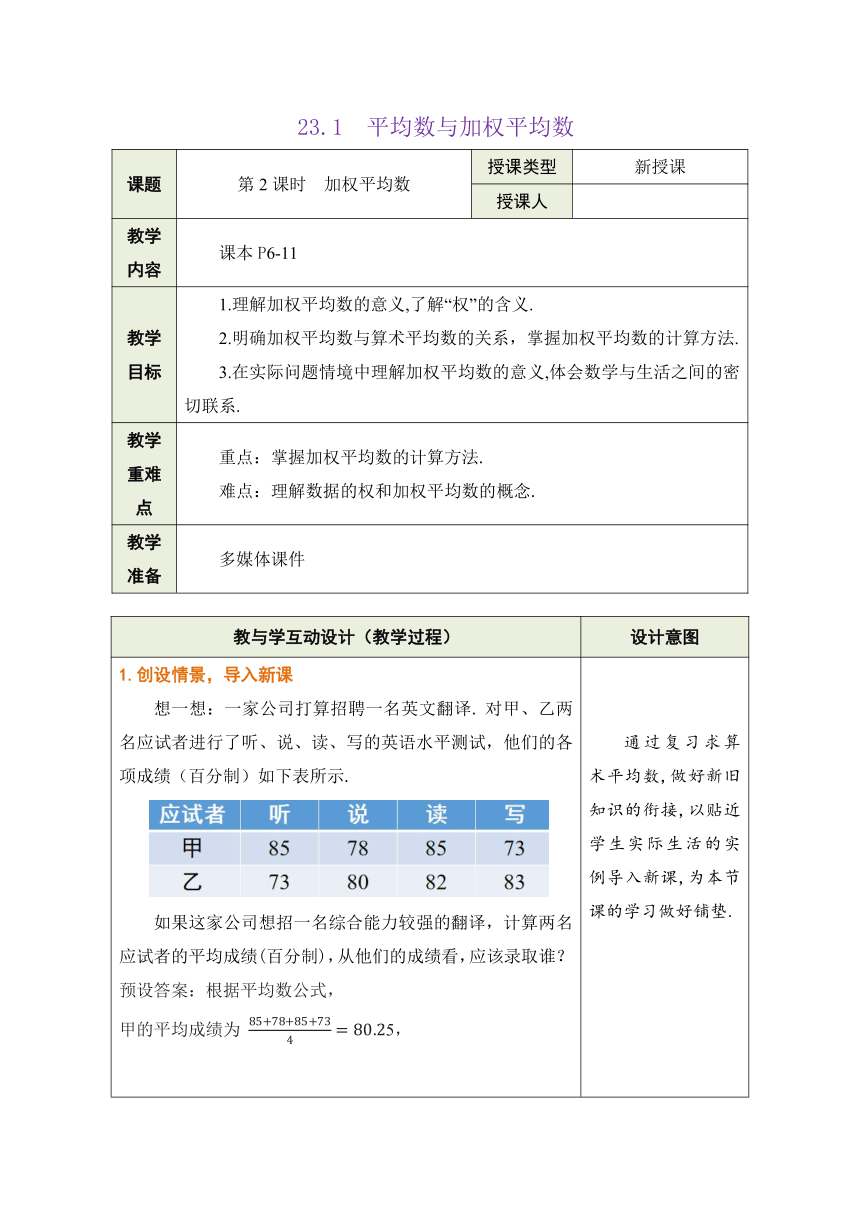
1.创设情景,导入新课 想一想:一家公司打算招聘一名英文翻译. 对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们的各项成绩(百分制)如下表所示. 如果这家公司想招一名综合能力较强的翻译,计算两名应试者的平均成绩(百分制),从他们的成绩看,应该录取谁? 预设答案:根据平均数公式, 甲的平均成绩为 5, 乙的平均成绩为 因为甲的平均成绩比乙高,所以应该录取甲. 师生活动:学生思考后小组合作交流,小组代表发言,教师展示解法,导出新课. 通过复习求算术平均数,做好新旧知识的衔接,以贴近学生实际生活的实例导入新课,为本节课的学习做好铺垫.
2.实践探究,学习新知 1.加权平均数的概念 【观察与思考】 问题1 假期里,小红和小惠结伴去买菜,三次购买的西红柿价格和数量如下表: 从平均价格来看,谁买的西红柿要便宜一些? 思考小亮和小明的下列说法,你认为他俩谁说得对?为什么? 预设答案:小红购买不同单价的西红柿的数量不同,所以平均价格不是三个单价的平均数.实际上,平均价格是总花费金额与购买总量的比. 所以: 从平均价格看,小红买的西红柿要便宜些. 师生活动:小组内合作交流,判断两个人的说法谁正确,教师对学生的回答进行点评,并引导学生通过计算平均数比较谁买的西红柿更便宜,学生独立完成计算平均数的过程,教师点评. 【归纳概念】 已知n个数,…,,若,…,为一组正数,则把 叫做n个数,…,的加权平均数,w1,w2,…,wn分别叫做这n个数的权重,简称为权. 教师提问: (1)在“共同探究”中,加权平均数是多少 哪些数是权 预设答案:小红购买的西红柿平均价格约为2.67元/千克,它是数4,3,2的加权平均数,三个数的权分别为1,2,3。 你能举出用加权平均数计算平均数的生活实例吗 师生活动:学生小组合作交流,创设不同的求平均数的生活情境,小组代表展示问题后,其他学生完成解答,教师进行点评,以鼓励学生参与为主. 【例题】 例1 某学校为了鼓励学生积极参加体育锻炼,规定体育科目学期成绩满分为100分,其中平时表现(早操、课外体育活动)、期中考试和期末考试成绩按比例3∶2∶5计入学期总成绩.甲、乙两名同学的各项成绩如下: 学生平时表现/分期中考试/分期末考试/分甲959085乙809588
分别计算甲、乙的学期总成绩. 解:三项成绩按3∶2∶5的比例确定,就是分别用3,2,5作为三项成绩的权,用加权平均数作为学期总成绩. 甲的学期总成绩为=89(分), 乙的学期总成绩为=87(分). 思考: (1)分配的“权”不同,甲、乙二人的总成绩是否会发生变化 回答:分配的“权”不同,甲、乙二人的总成绩会发生变化. (2)算术平均数和加权平均数的区别和联系是什么 回答:算术平均数是加权平均数的一种特殊情况(它特殊在各项的权相等);在实际问题中,各项权不相等时,计算平均数时就要采用加权平均数. 做一做 某电视节目主持人大赛要进行专业素质、综合素质、外语水平和临场应变能力四项测试,各项测试均采用10分制,两名选手的各项测试成绩如下表所示: 测试项目专业 素质综合 素质外语 水平临场应 变能力测试成 绩/分甲9.08.57.58.8乙8.09.28.49.0
(1)如果按四项测试成绩的算术平均数排名次,名次是怎样的 (2)如果规定按专业素质、综合素质、外语水平和临场应变能力四项测试的成绩各占60%,20%,10%,10%计算总成绩,名次有什么变化 解:(1)甲、乙各项成绩的算术平均数分别为: =8.45(分), =8.65(分). 比较算术平均数,乙排名第一,甲排名第二. (2)甲、乙的加权平均成绩分别为: =9.0×60%+8.5×20%+7.5×10%+8.8×10%=8.73(分), =8.0×60%+9.2×20%+8.4×10%+9.0×10%=8.38(分). 比较加权平均数,甲排名第一,乙排名第二. 【归纳总结】 比较加权平均数,甲排名第一,乙排名第二. 总结:权主要有三种表现形式:百分比,比例,数据出现的次数. 老师带领总结加权平均数的意义 加权平均数不仅与每个数据的大小有关,还受每个数据的权的影响. 数据的“权”反映数据的“重要程度”. 权越大,该数据所占的比重越大;反之,权越小,该数据所占的比重越小. 注意:(1)一组数据的平均数是唯一的. (2)平均数的单位要与原数据的单位一致. 2.估测数据的平均数 目测教室黑板的宽度,然后汇总,计算出全班同学估测数据的平均数,并实际测量,比较各小组的平均数波动情况和全班同学平均数与测量结果的误差. 师生活动:学生以小组为单位,先进行目测,并计算出结果,然后全班汇总,教师重在组织并引导学生观察. 例2 从某校九年级男生中,任意选出100人,分别测量他们的体重,将数据进行分组整理,结果如下表: 计算这100名男生的平均体重. 解:五组数据的组中值分别为47,53,59,65,71.加权平均数为 所以,这100名男生的平均体重约为59.6kg. 师生活动:学生独立完成后,小组内交流答案,小组代表板书解答过程,教师在巡视过程中帮助有困难的学生,对学生的展示进行点评. 通过解决生活实际问题,引导学生思考重要性的差异对平均数的影响,为加权平均数概念的形成做好铺垫,在探究过程中,充分发挥学生的主观能动性,让学生积极思考,合作交流,在数学活动中逐步形成概念. 教师设计开放性题目,学生通过合作交流,共同创设问题情境,体会“权”对平均数的影响,加深学生对加权平均数的理解,提高学生的发散性思维,达到学生数学能力的提升. 学会利用加权平均数进行运算,加深对所学知识的理解,提高学生知识的综合运用能力. 巩固所学知识,加深对所学知识的理解,提高学生知识的综合运用能力. 通过实际动手,让学生体会在实际生活中,我们经常要对某个量进行测量,测量时,往往会产生误差,为了得到比较准确的结果,可以进行多次重复的测量,用这些测量值的平均数作为这个量的估计值. 让学生明白加权平均数的权,有时是一组数据的组中值.
3.学以致用,应用新知 考点 加权平均数的计算 练习1 一次演讲比赛中,评委将从演讲内容、演讲能力、演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%、演讲能力占40%、演讲效果占10%,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示,请确定两人的名次. 解:选手A的最后得分是 选手B的最后得分是 由上可知选手B获得第一名,选手A获得第二名. 变式训练1 某单位定期对员工的专业知识、工作业绩、出勤情况三个方面进行考核(考核的满分均为100分),三个方面的重要性之比为3:5:2.小王经过考核后所得的分数依次为90分、88分、83分,那么小王的最后得分是( ) A. 87 分 B. 87. 5 分 C.87.6 分 D. 88 分 答案:C 练习2 某公交公司为了了解673路公交汽车的运营情况,该公司统计了某天673路公共汽车每个运行班次的载客量,得到下面的图表: 载客量组中值频数(班次)1≤x<2111321≤x<4131541≤x<61a2061≤x<81712281≤x<1019118101≤x
4.随堂训练,巩固新知 1.某超市销售A , B , C , D四种矿泉水,它们的单价依次是5元、3元、2元、1元.某天的销售情况如图所示,则这天销售的矿泉水的平均单价是( ) A.1.95 元 B.2. 15 元 C.2. 25 元 D.2.75 元 答案:C 2.某校拟招聘一批优秀教师,其中某位教师笔试、试讲、面试三轮测试成绩分别为92分、 85分、90分,综合成绩笔试占40%,试讲占40%,面试占20%,则该名教师的综合成绩为______分. 答案:88.8 3.某跳水队为了解运动员的年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个跳水队运动员的平均年龄(结果取整数). 解:这个跳水队运动员的平均年龄为 ≈14(岁). 4.如果某家公司想招一名笔译能力较强的翻译,听、说、读、写的成绩按照2:1:3:4的比确定,计算两名应试者的平均成绩(百分制).从他们的成绩看,应该录取谁? 解: 因为乙的成绩比甲高,所以应该录取乙. 5.某部队为测量一批新制造的炮弹的杀伤半径,从中抽查了50枚炮弹,它们的杀伤半径(米)如下表所示: 求这批炮弹的平均杀伤半径. 解:由表可得出各组数据的组中值分别是30,50,70,90, ∴这批炮弹的平均杀伤半径大约是60. 8米. 通过本环节的学习,让学生巩固所学知识.
5.课堂小结,自我完善 w1,w2,…,wn分别叫做这n个数的权重,简称为权. 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容.
6.布置作业 课本P8习题A组,P9习题B组,P11习题A组 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 23.1 平均数与加权平均数 第2课时 加权平均数 1.加权平均数 概念: 2.例题讲解 3.随堂练习 4.估测数据的平均数 5.课堂小结 6.作业布置 提纲掣领,重点突出.
教后反思 通过教学,预定的目标已经达到.学生主动参与面广,学习兴趣浓,练习的达成度高,教师得到了解放,学生也得到了一次锻炼的机会,很多学生从自学中找到了自信,转变了自己的学习方式,从过度依赖老师转到了先自学再提问,培养了自己的自学能力与独立思考问题的能力. 反思,更进一步提升.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
