23.3方差(第2课时 方差的应用) 教学设计(表格式)冀教版数学九年级上册
文档属性
| 名称 | 23.3方差(第2课时 方差的应用) 教学设计(表格式)冀教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 393.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-20 00:00:00 | ||
图片预览


文档简介
23.3 方差
课题 第2课时 方差的应用 授课类型 新授课
授课人
教学内容 课本P22-25
教学目标 1.组数据的方差,会用方差分析数据的离散程度. 2.学会从图中提取信息,提高读图能力. 3.会用合适的统计量去分析数据,提高决策能力.
教学重难点 重点:能准确计算一组数据的方差,会用方差分析数据的离散程度. 难点:用方差分析数据的离散程度.
教学准备 多媒体课件
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 如何求一组数据的方差,方差的意义是什么? 预设答案: 方差用来衡量一组数据的波动大小(即这组数据偏离平均数的大小). 方差越大,数据的波动越大;方差越小,数据的波动越小. 师生活动:学生思考后举手回答,教师点评. 通过复习旧知衔接新知,引出新课.
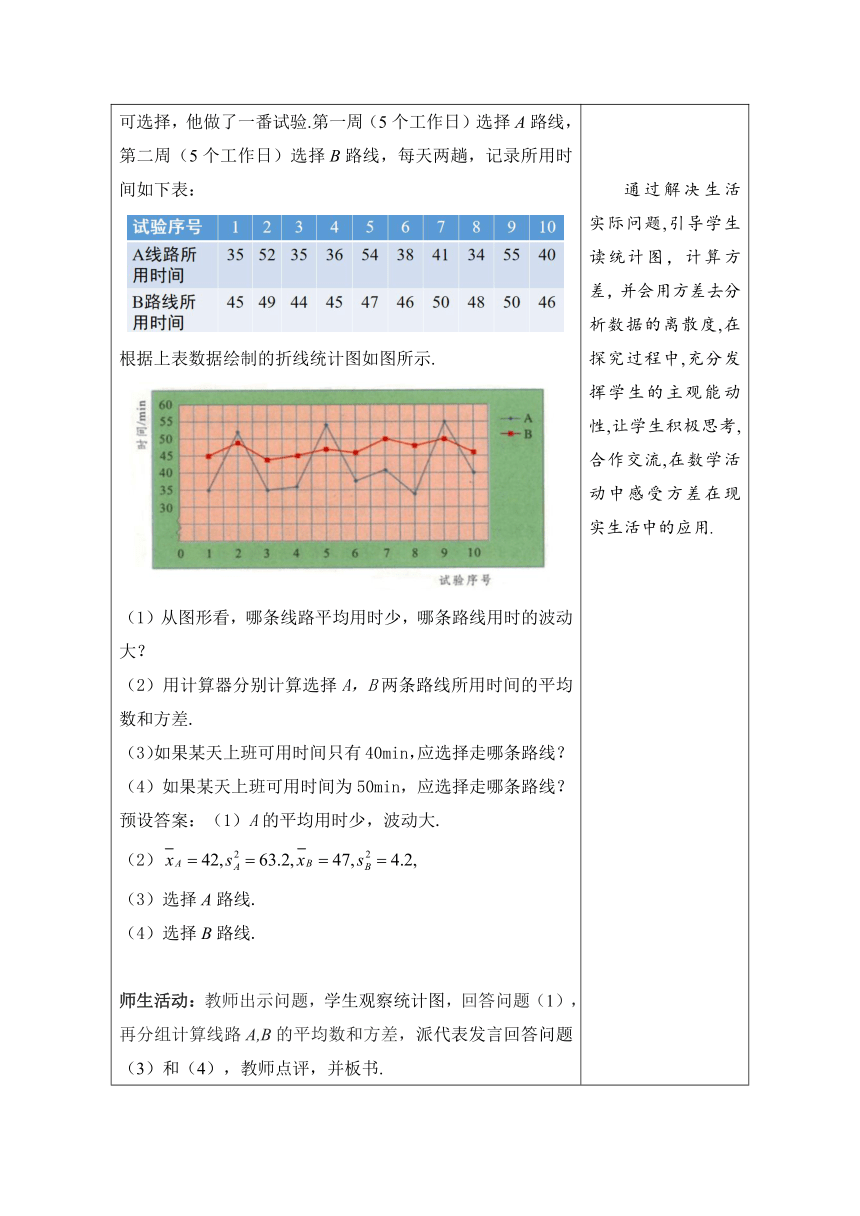
2.实践探究,学习新知 【探究】 问题1 张老师乘公交车上班,从家到学校有A,B两条路线可选择,他做了一番试验.第一周(5个工作日)选择A路线,第二周(5个工作日)选择B路线,每天两趟,记录所用时间如下表: 根据上表数据绘制的折线统计图如图所示. (1)从图形看,哪条线路平均用时少,哪条路线用时的波动大? (2)用计算器分别计算选择A,B两条路线所用时间的平均数和方差. (3)如果某天上班可用时间只有40min,应选择走哪条路线? (4)如果某天上班可用时间为50min,应选择走哪条路线? 预设答案:(1)A的平均用时少,波动大. (2) (3)选择A路线. (4)选择B路线. 师生活动:教师出示问题,学生观察统计图,回答问题(1),再分组计算线路A,B的平均数和方差,派代表发言回答问题(3)和(4),教师点评,并板书. 【教材例题】 例1 测试甲、乙两个品牌的手表各50只,根据日走时误差数据绘制的统计图如下图所示,从日走时误差角度分析这两个品牌手表的优劣. (1)你会想到用哪个统计量去做比较?平均数越大越好吗? 预设答案:平均数是首选,因为平均数代表的是平均水平. 由于我们考察的数据是手表日走时误差,所以平均数与0越接近,说明误差越小,质量越好. 计算甲、乙两品牌手表日走时误差的平均数: 我们发现两个品牌的平均数相同,单从平均数角度难以判断甲、乙的优劣. 师生活动:教师出示问题,学生独立完成计算平均数,发现平均数相同,分组讨论,是否可以判断甲乙的优劣,教学点评,最终给出答案并板书. (2)平均数相同的情况下,我们还可以通过什么统计量来比较甲、乙两个品牌手表日走时误差的优劣? 分析:由于手表的日走时误差为0时最标准,与0的偏差越小,质量越好.因此我们需要去明确两组数据相对于0的波动情况,即需要计算并比较甲、乙方差的大小. 解:=×[(-2×5+(-1×11+×17+×13+×4]=1.2, =×[(-3×2+(-2×6+×11+02×14+×8+×6+×3]=2.24, (3)观察两种手表日走时误差的分布范围,你有什么发现? 预设答案:甲品牌的误差分布范围在-2到2之间,乙品牌的误差范围在-3到3之间,甲品牌的误差范围较小,所以甲品牌手表优于乙品牌手表. (4)若规定日走时误差的绝对值不超过1 s为优秀,判断甲、乙的优劣. 预设答案:甲的优秀率=(11+17+13)÷50×100%=82%. 乙的优秀率=(11+14+8)÷50×100%=66%. 82%>66% ∴甲品牌优于乙品牌. 师生活动:学生独立计算两种数据的方差后,小组内交流答案,并思考回答问题(3)和(4),教师在巡视过程中帮助有困难的学生,对学生的回答进行点评,并板书. 【归纳总结】 在比较两组数据时,一般先看平均数,在平均数相同或相近的情况下,再分析稳定性问题,而方差是反映数据的波动大小的量,通过比较方差的大小来解决问题. 通过解决生活实际问题,引导学生读统计图,计算方差,并会用方差去分析数据的离散度,在探究过程中,充分发挥学生的主观能动性,让学生积极思考,合作交流,在数学活动中感受方差在现实生活中的应用. 用统计量去分析数据,一般先考虑平均数,当平均数相同时,再考虑其它统计量,为后续用统计量-方差分析数据打下基础. 学会用统计量方差去分析生活实例中的数据,并用分析的结果解决相应的实际问题.
3.学以致用,应用新知 考点1 方差的应用 练习1 某快餐公司的香辣鸡腿很受消费者欢迎.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近.快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿.检查人员从两家的鸡腿中各随机抽取15个,记录它们的质量(单位:g)如表所示.根据表中数据,你认为快餐公司应该选购哪家加工厂的鸡腿? 解:检查人员从甲、乙两家农副产品加工厂各随机抽取的15个鸡腿分别组成一个样本,样本数据的平均数分别是 样本数据的方差分别是 由可知,两家加工厂的鸡腿质量大致相等; 由s2甲 < s2乙 可知,甲加工厂的鸡腿质量更稳定,大小更均匀. 因此,快餐公司应该选购甲加工厂生产的鸡腿. 变式训练1 现有甲、乙两个合唱队,队员的平均身高为170 cm,方差分别是s2甲,s2乙,且s2甲>s2乙,,则两个队的队员的身高较整齐的是( B ) 甲队 B.乙队 C.两队一样整齐 D.不能确定 答案:C 巩固所学知识,加深用方差去分析数据的理解,提高学生知识的综合运用能力.
4.随堂训练,巩固新知 1.在体育课上,甲、乙两名同学分别进行了5次跳远测试,经计算他们的平均成绩相同,若要比较这两名同学的成绩哪一个更为稳定,通常需要比较他们成绩的( ) A.众数 B.平均数 C.中位数 D.方差 答案:D 2.某村引进甲、乙两种水稻,各选6块条件相同的试验田吗,结果甲、乙两种水稻的平均产量均为550kg/亩,甲的方差=141.7,乙的方差=433.3,则产量稳定,适合推广的品种为( ) A.甲、乙均可 B.乙 C.甲 D.无法判断 答案:C 3.某排球队6名场上队员的身高(单位:cm)是:180 184 188 190 192 194.先用一名身高为186cm的队员换下场上身高为192cm的队员,与换人前相比,场上队员的身高( ) A.平均数变小,方差变小. B.平均数变小,方差变大. C.平均数变大,方差变小. D.平均数变大,方差变大. 答案:A 通过本环节的学习,让学生巩固所学知识.
5.课堂小结,自我完善 本节课你有什么收获? 1.平均数是衡量、比较两组数据优劣的首选统计量. 2.当两组数据平均水平相同或相近时,通常会用方差比较优劣. 3.当数据中出现极端值时,方差会变大,此时平均数对数据的代表性变差; 反之,方差小时,说明数据中没有异常值,此时平均数对数据的代表性较好. 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容.
6.布置作业 课本P24习题A组、B组 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 23.3 方差 第2课时 方差的应用 1.平均数和方差的公式: 2.方差的意义: 3.根据平均数和方差的大小衡量数据的优劣: 提纲掣领,重点突出.
教后反思 本课时的重点是根据平均数和方差判断数据的好坏.当平均水平相同时,就要分析数据的稳定性,根据方差的大小来判断数据的稳定性;当方差大小相同时,平均数大的就代表这组数据比较好. 反思,更进一步提升.
课题 第2课时 方差的应用 授课类型 新授课
授课人
教学内容 课本P22-25
教学目标 1.组数据的方差,会用方差分析数据的离散程度. 2.学会从图中提取信息,提高读图能力. 3.会用合适的统计量去分析数据,提高决策能力.
教学重难点 重点:能准确计算一组数据的方差,会用方差分析数据的离散程度. 难点:用方差分析数据的离散程度.
教学准备 多媒体课件
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 如何求一组数据的方差,方差的意义是什么? 预设答案: 方差用来衡量一组数据的波动大小(即这组数据偏离平均数的大小). 方差越大,数据的波动越大;方差越小,数据的波动越小. 师生活动:学生思考后举手回答,教师点评. 通过复习旧知衔接新知,引出新课.
2.实践探究,学习新知 【探究】 问题1 张老师乘公交车上班,从家到学校有A,B两条路线可选择,他做了一番试验.第一周(5个工作日)选择A路线,第二周(5个工作日)选择B路线,每天两趟,记录所用时间如下表: 根据上表数据绘制的折线统计图如图所示. (1)从图形看,哪条线路平均用时少,哪条路线用时的波动大? (2)用计算器分别计算选择A,B两条路线所用时间的平均数和方差. (3)如果某天上班可用时间只有40min,应选择走哪条路线? (4)如果某天上班可用时间为50min,应选择走哪条路线? 预设答案:(1)A的平均用时少,波动大. (2) (3)选择A路线. (4)选择B路线. 师生活动:教师出示问题,学生观察统计图,回答问题(1),再分组计算线路A,B的平均数和方差,派代表发言回答问题(3)和(4),教师点评,并板书. 【教材例题】 例1 测试甲、乙两个品牌的手表各50只,根据日走时误差数据绘制的统计图如下图所示,从日走时误差角度分析这两个品牌手表的优劣. (1)你会想到用哪个统计量去做比较?平均数越大越好吗? 预设答案:平均数是首选,因为平均数代表的是平均水平. 由于我们考察的数据是手表日走时误差,所以平均数与0越接近,说明误差越小,质量越好. 计算甲、乙两品牌手表日走时误差的平均数: 我们发现两个品牌的平均数相同,单从平均数角度难以判断甲、乙的优劣. 师生活动:教师出示问题,学生独立完成计算平均数,发现平均数相同,分组讨论,是否可以判断甲乙的优劣,教学点评,最终给出答案并板书. (2)平均数相同的情况下,我们还可以通过什么统计量来比较甲、乙两个品牌手表日走时误差的优劣? 分析:由于手表的日走时误差为0时最标准,与0的偏差越小,质量越好.因此我们需要去明确两组数据相对于0的波动情况,即需要计算并比较甲、乙方差的大小. 解:=×[(-2×5+(-1×11+×17+×13+×4]=1.2, =×[(-3×2+(-2×6+×11+02×14+×8+×6+×3]=2.24, (3)观察两种手表日走时误差的分布范围,你有什么发现? 预设答案:甲品牌的误差分布范围在-2到2之间,乙品牌的误差范围在-3到3之间,甲品牌的误差范围较小,所以甲品牌手表优于乙品牌手表. (4)若规定日走时误差的绝对值不超过1 s为优秀,判断甲、乙的优劣. 预设答案:甲的优秀率=(11+17+13)÷50×100%=82%. 乙的优秀率=(11+14+8)÷50×100%=66%. 82%>66% ∴甲品牌优于乙品牌. 师生活动:学生独立计算两种数据的方差后,小组内交流答案,并思考回答问题(3)和(4),教师在巡视过程中帮助有困难的学生,对学生的回答进行点评,并板书. 【归纳总结】 在比较两组数据时,一般先看平均数,在平均数相同或相近的情况下,再分析稳定性问题,而方差是反映数据的波动大小的量,通过比较方差的大小来解决问题. 通过解决生活实际问题,引导学生读统计图,计算方差,并会用方差去分析数据的离散度,在探究过程中,充分发挥学生的主观能动性,让学生积极思考,合作交流,在数学活动中感受方差在现实生活中的应用. 用统计量去分析数据,一般先考虑平均数,当平均数相同时,再考虑其它统计量,为后续用统计量-方差分析数据打下基础. 学会用统计量方差去分析生活实例中的数据,并用分析的结果解决相应的实际问题.
3.学以致用,应用新知 考点1 方差的应用 练习1 某快餐公司的香辣鸡腿很受消费者欢迎.现有甲、乙两家农副产品加工厂到快餐公司推销鸡腿,两家鸡腿的价格相同,品质相近.快餐公司决定通过检查鸡腿的质量来确定选购哪家的鸡腿.检查人员从两家的鸡腿中各随机抽取15个,记录它们的质量(单位:g)如表所示.根据表中数据,你认为快餐公司应该选购哪家加工厂的鸡腿? 解:检查人员从甲、乙两家农副产品加工厂各随机抽取的15个鸡腿分别组成一个样本,样本数据的平均数分别是 样本数据的方差分别是 由可知,两家加工厂的鸡腿质量大致相等; 由s2甲 < s2乙 可知,甲加工厂的鸡腿质量更稳定,大小更均匀. 因此,快餐公司应该选购甲加工厂生产的鸡腿. 变式训练1 现有甲、乙两个合唱队,队员的平均身高为170 cm,方差分别是s2甲,s2乙,且s2甲>s2乙,,则两个队的队员的身高较整齐的是( B ) 甲队 B.乙队 C.两队一样整齐 D.不能确定 答案:C 巩固所学知识,加深用方差去分析数据的理解,提高学生知识的综合运用能力.
4.随堂训练,巩固新知 1.在体育课上,甲、乙两名同学分别进行了5次跳远测试,经计算他们的平均成绩相同,若要比较这两名同学的成绩哪一个更为稳定,通常需要比较他们成绩的( ) A.众数 B.平均数 C.中位数 D.方差 答案:D 2.某村引进甲、乙两种水稻,各选6块条件相同的试验田吗,结果甲、乙两种水稻的平均产量均为550kg/亩,甲的方差=141.7,乙的方差=433.3,则产量稳定,适合推广的品种为( ) A.甲、乙均可 B.乙 C.甲 D.无法判断 答案:C 3.某排球队6名场上队员的身高(单位:cm)是:180 184 188 190 192 194.先用一名身高为186cm的队员换下场上身高为192cm的队员,与换人前相比,场上队员的身高( ) A.平均数变小,方差变小. B.平均数变小,方差变大. C.平均数变大,方差变小. D.平均数变大,方差变大. 答案:A 通过本环节的学习,让学生巩固所学知识.
5.课堂小结,自我完善 本节课你有什么收获? 1.平均数是衡量、比较两组数据优劣的首选统计量. 2.当两组数据平均水平相同或相近时,通常会用方差比较优劣. 3.当数据中出现极端值时,方差会变大,此时平均数对数据的代表性变差; 反之,方差小时,说明数据中没有异常值,此时平均数对数据的代表性较好. 通过小结,使学生梳理本节课所学内容,掌握本节课的核心内容.
6.布置作业 课本P24习题A组、B组 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 23.3 方差 第2课时 方差的应用 1.平均数和方差的公式: 2.方差的意义: 3.根据平均数和方差的大小衡量数据的优劣: 提纲掣领,重点突出.
教后反思 本课时的重点是根据平均数和方差判断数据的好坏.当平均水平相同时,就要分析数据的稳定性,根据方差的大小来判断数据的稳定性;当方差大小相同时,平均数大的就代表这组数据比较好. 反思,更进一步提升.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
