25.2 平行线分线段成比例(第1课时 平行线分线段成比例的基本事实) 教学设计(表格式)冀教版数学九年级上册
文档属性
| 名称 | 25.2 平行线分线段成比例(第1课时 平行线分线段成比例的基本事实) 教学设计(表格式)冀教版数学九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-20 07:57:18 | ||
图片预览


文档简介
25.2 平行线分线段成比例
课题 第1课时 平行线分线段成比例的基本事实 授课类型 新授课
授课人
教学内容 课本P63-65
教学目标 1.了解平行线分线段成比例这个基本事实产生的过程. 2.掌握平行线分线段成比例的基本事实. 3.会用平行线分线段成比例的基本事实解决相关的计算和证明问题.
教学重难点 重点:平行线分线段成比例的基本事实及其应用. 难点:会用平行线分线段成比例的的基本事实解决相关的计算和证明问题.
教学准备 多媒体课件
教与学互动设计(教学过程) 设计意图
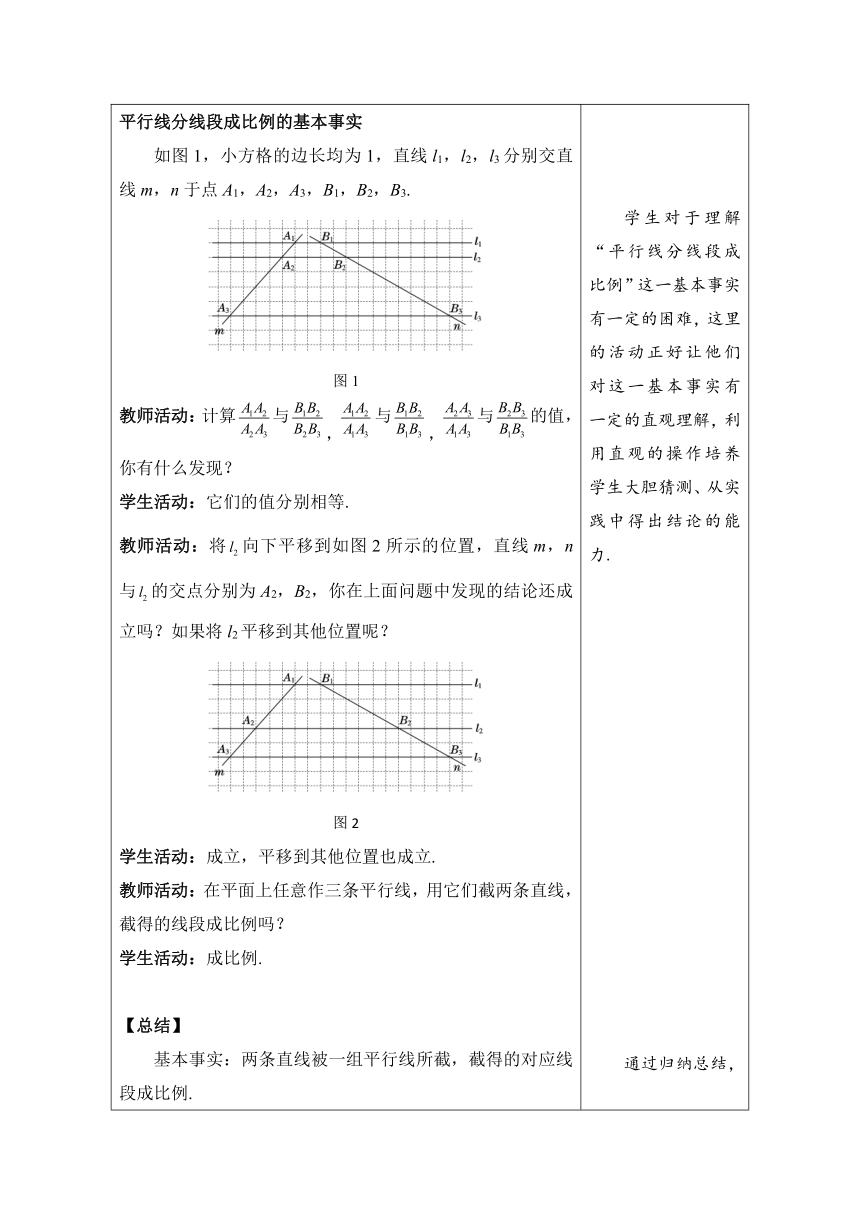
1.创设情景,导入新课 比例线段的内容是什么? 如图,l1∥l2∥l3,AB=BC,=__________,DE=EF,=________. 与有什么关系? 通过特殊图形,对平行线分线段成比例有点认识.
2.实践探究,学习新知 【探究】 平行线分线段成比例的基本事实 如图1,小方格的边长均为1,直线l1,l2,l3分别交直线m,n于点A1,A2,A3,B1,B2,B3. 图1 教师活动:计算与,与,与的值,你有什么发现? 学生活动:它们的值分别相等. 教师活动:将向下平移到如图2所示的位置,直线m,n与的交点分别为A2,B2,你在上面问题中发现的结论还成立吗?如果将l2平移到其他位置呢? 图2 学生活动:成立,平移到其他位置也成立. 教师活动:在平面上任意作三条平行线,用它们截两条直线,截得的线段成比例吗? 学生活动:成比例. 【总结】 基本事实:两条直线被一组平行线所截,截得的对应线段成比例. 符号语言: 若l1∥l2∥l3,则. 若l1∥l2∥l3,则. 知识拓展:(1)理解“对应”的含义:对应线段成比例是指所得的对应位置的线段成比例,如. (2)平行线分线段成比例的基本事实与平行直线和被截两直线的交点位置无关. 【练习】 如图3所示,在正方形网格图中,每个正方形的边长均为1,若AB=BC,则DE和EF之间有什么关系 为什么 图3 解:DE=EF. 理由如下:∵ AD∥BE∥CF,∴ . ∵ AB=BC,∴ =1, ∴ DE=EF. 学生对于理解“平行线分线段成比例”这一基本事实有一定的困难,这里的活动正好让他们对这一基本事实有一定的直观理解,利用直观的操作培养学生大胆猜测、从实践中得出结论的能力. 通过归纳总结,使学生掌握平行线分线段成比例的基本事实,为解决此类问题打下坚实基础.
3.学以致用,应用新知 考点1 由平行判断成比例的线段 练习1 如图,已知直线AB∥CD∥EF,下列结论中不成立的是( ) 图4 A. B. C. D. 答案:D 变式训练1 如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A,B,C和D,E,F,已知=,若DF=10,则的长为( ) 答案:D 巩固由平行判断成比例线段的方法,加深对所学知识的理解,提高学生知识的综合运用能力.
4.随堂训练,巩固新知 1.如图5,已知l1∥l2∥l3,下列比例式错误的是( ) A. B. C. D. 图5 图6 答案:D 2.如图6,已知l1∥l2∥l3,AC=4,,CE=6,BD=3,则DF=( ) A.2 B.4.5 C.6 D.8 答案:B 3. 如图7,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若=,DE=4,则EF的长是______. 图 7 图8 答案:6 4.如图8,已知直线a∥b∥c,分别交直线m,n于点A,C,E,B,D,F,AC=4,CE=6,BD=3,求BF的长. 解:∵ a∥b∥c, ∴ 即, ∴ 4DF=3×6,∴ DF=, ∴ BF=BD+DF=3+. 知识的综合运用,通过本环节的学习,让学生巩固所学知识.
5.课堂小结,自我完善 本节课所学知识:平行线分线段成比例的基本事实. 平行线分线段成比例的基本事实:两条直线被一组平行线所截,截得的对应线段成比例. 通过学生自我反思、小组交流、引导学生自主完成对本节重要知识技能和思想方法的小结.
6.布置作业 课本P64习题A组,P65习题B组 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 25.2 平行线分线段成比例 第1课时 平行线分线段成比例的基本事实 平行线分线段成比例的基本事实:两条直线被一组平行线所截,截得的对应线段成比例. 提纲掣领,重点突出.
教后反思 本节课主要采用了讨论探究法,平行线分线段成比例是学习相似三角形的基础,教学中通过具体图形,计算数据来探究平行线分线段成比例,培养了学生的自学探究能力,而且这样比较直观,学生容易理解.通过例题讲解及练习,增加了学生的知识,及应用能力.不足之处,学生对于对应关系找不准确,还需要加强这方面的练习. 反思,更进一步提升.
课题 第1课时 平行线分线段成比例的基本事实 授课类型 新授课
授课人
教学内容 课本P63-65
教学目标 1.了解平行线分线段成比例这个基本事实产生的过程. 2.掌握平行线分线段成比例的基本事实. 3.会用平行线分线段成比例的基本事实解决相关的计算和证明问题.
教学重难点 重点:平行线分线段成比例的基本事实及其应用. 难点:会用平行线分线段成比例的的基本事实解决相关的计算和证明问题.
教学准备 多媒体课件
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 比例线段的内容是什么? 如图,l1∥l2∥l3,AB=BC,=__________,DE=EF,=________. 与有什么关系? 通过特殊图形,对平行线分线段成比例有点认识.
2.实践探究,学习新知 【探究】 平行线分线段成比例的基本事实 如图1,小方格的边长均为1,直线l1,l2,l3分别交直线m,n于点A1,A2,A3,B1,B2,B3. 图1 教师活动:计算与,与,与的值,你有什么发现? 学生活动:它们的值分别相等. 教师活动:将向下平移到如图2所示的位置,直线m,n与的交点分别为A2,B2,你在上面问题中发现的结论还成立吗?如果将l2平移到其他位置呢? 图2 学生活动:成立,平移到其他位置也成立. 教师活动:在平面上任意作三条平行线,用它们截两条直线,截得的线段成比例吗? 学生活动:成比例. 【总结】 基本事实:两条直线被一组平行线所截,截得的对应线段成比例. 符号语言: 若l1∥l2∥l3,则. 若l1∥l2∥l3,则. 知识拓展:(1)理解“对应”的含义:对应线段成比例是指所得的对应位置的线段成比例,如. (2)平行线分线段成比例的基本事实与平行直线和被截两直线的交点位置无关. 【练习】 如图3所示,在正方形网格图中,每个正方形的边长均为1,若AB=BC,则DE和EF之间有什么关系 为什么 图3 解:DE=EF. 理由如下:∵ AD∥BE∥CF,∴ . ∵ AB=BC,∴ =1, ∴ DE=EF. 学生对于理解“平行线分线段成比例”这一基本事实有一定的困难,这里的活动正好让他们对这一基本事实有一定的直观理解,利用直观的操作培养学生大胆猜测、从实践中得出结论的能力. 通过归纳总结,使学生掌握平行线分线段成比例的基本事实,为解决此类问题打下坚实基础.
3.学以致用,应用新知 考点1 由平行判断成比例的线段 练习1 如图,已知直线AB∥CD∥EF,下列结论中不成立的是( ) 图4 A. B. C. D. 答案:D 变式训练1 如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A,B,C和D,E,F,已知=,若DF=10,则的长为( ) 答案:D 巩固由平行判断成比例线段的方法,加深对所学知识的理解,提高学生知识的综合运用能力.
4.随堂训练,巩固新知 1.如图5,已知l1∥l2∥l3,下列比例式错误的是( ) A. B. C. D. 图5 图6 答案:D 2.如图6,已知l1∥l2∥l3,AC=4,,CE=6,BD=3,则DF=( ) A.2 B.4.5 C.6 D.8 答案:B 3. 如图7,l1∥l2∥l3,直线a,b与l1,l2,l3分别相交于点A,B,C和点D,E,F.若=,DE=4,则EF的长是______. 图 7 图8 答案:6 4.如图8,已知直线a∥b∥c,分别交直线m,n于点A,C,E,B,D,F,AC=4,CE=6,BD=3,求BF的长. 解:∵ a∥b∥c, ∴ 即, ∴ 4DF=3×6,∴ DF=, ∴ BF=BD+DF=3+. 知识的综合运用,通过本环节的学习,让学生巩固所学知识.
5.课堂小结,自我完善 本节课所学知识:平行线分线段成比例的基本事实. 平行线分线段成比例的基本事实:两条直线被一组平行线所截,截得的对应线段成比例. 通过学生自我反思、小组交流、引导学生自主完成对本节重要知识技能和思想方法的小结.
6.布置作业 课本P64习题A组,P65习题B组 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 25.2 平行线分线段成比例 第1课时 平行线分线段成比例的基本事实 平行线分线段成比例的基本事实:两条直线被一组平行线所截,截得的对应线段成比例. 提纲掣领,重点突出.
教后反思 本节课主要采用了讨论探究法,平行线分线段成比例是学习相似三角形的基础,教学中通过具体图形,计算数据来探究平行线分线段成比例,培养了学生的自学探究能力,而且这样比较直观,学生容易理解.通过例题讲解及练习,增加了学生的知识,及应用能力.不足之处,学生对于对应关系找不准确,还需要加强这方面的练习. 反思,更进一步提升.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
