25.2平行线分线段成比例(第2课时 平行线分线段成比例的基本事实的推论) 教学设计(表格式)冀教版数学九年级上册
文档属性
| 名称 | 25.2平行线分线段成比例(第2课时 平行线分线段成比例的基本事实的推论) 教学设计(表格式)冀教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-20 07:55:50 | ||
图片预览


文档简介
25.2 平行线分线段成比例
课题 第2课时 平行线分线段成比例的基本事实的推论 授课类型 新授课
授课人
教学内容 课本P65-68
教学目标 1.掌握平行线分线段成比例的基本事实的推论. 2.了解平行于三角形一边的直线的性质. 3.会用平行线分线段成比例的基本事实的推论解决相关的计算和证明问题.
教学重难点 重点:平行线分线段成比例的基本事实的推论及其应用. 难点:会用平行线分线段成比例的基本事实的推论解决相关的计算和证明问题.
教学准备 多媒体课件
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 【回顾复行线分线段成比例的基本事实: 两条直线被一组平行线所截,截得的对应线段成比例. 图9 符号语言: 若l1 ∥l2∥ l3 ,则. 回顾复习上节课所学内容,有助于本节课的学习.
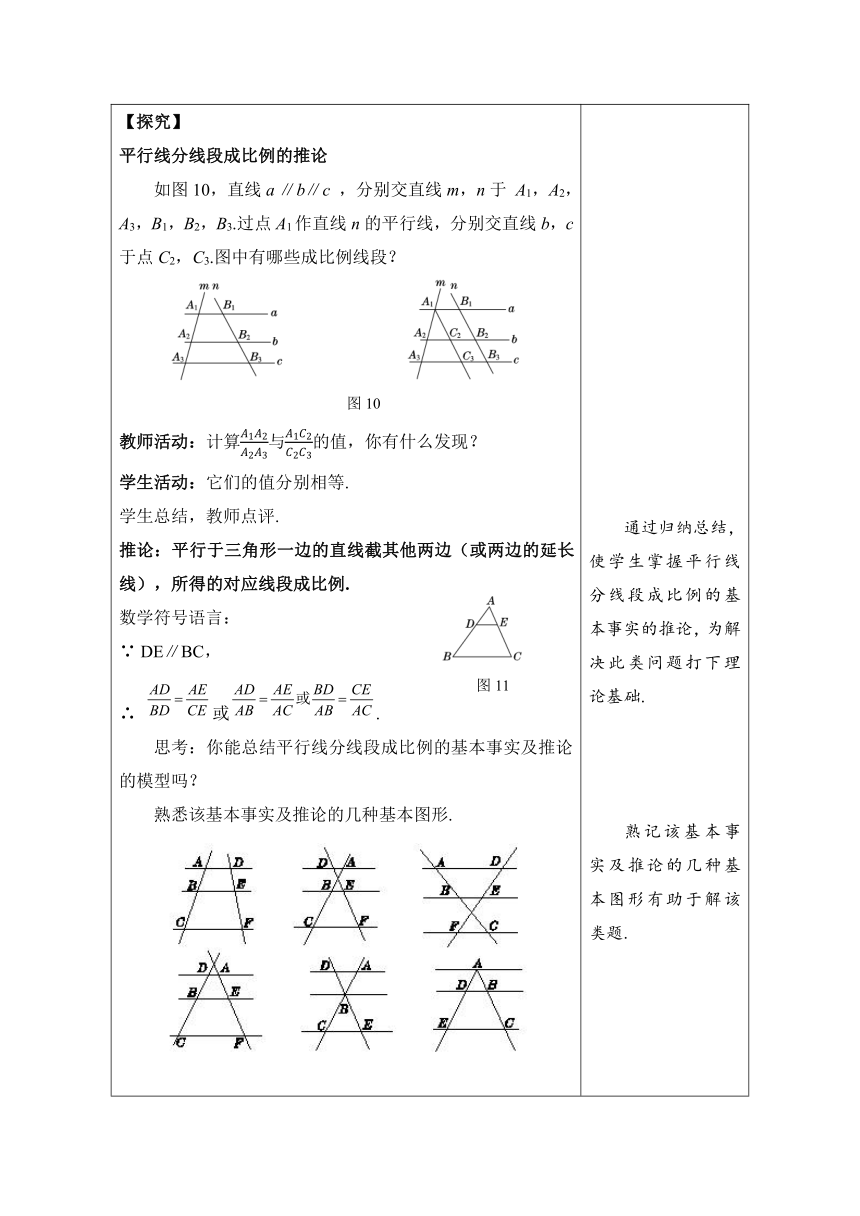
2.实践探究,学习新知 【探究】 平行线分线段成比例的推论 如图10,直线a ∥b∥c ,分别交直线m,n于 A1,A2,A3,B1,B2,B3.过点A1作直线n的平行线,分别交直线b,c于点C2,C3.图中有哪些成比例线段? 图10 教师活动:计算与的值,你有什么发现? 学生活动:它们的值分别相等. 学生总结,教师点评. 推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例. 数学符号语言: ∵ DE∥BC, ∴ 或. 思考:你能总结平行线分线段成比例的基本事实及推论的模型吗? 熟悉该基本事实及推论的几种基本图形. 【例题】 例1 如图12,在△ABC中,E,F分别是AB和AC上的点,且 EF∥BC, (1)如果AE = 7, EB = 5, FC = 4,那么AF的长是多少? (2)如果AB = 10, AE=6,AF = 5,那么FC的长是多少? 【问题探索】根据平行线分线段成比例的推论列出比例式,即可求出AF,FC的长. 解:(1)∵ EF∥BC,∴ . ∵ AE=7,EB=5,FC=4, ∴ ,∴ AF=. (2)∵ EF∥BC,∴ . ∵ AB=10,AE=6,AF=5, ∴ ∴ , ∴ FC=AC-AF=. 例2 如图13所示,在△ABC中,EF∥BC,EF与两边AB,AC分别相交于点E,F. 求证:. 证明:∵ EF∥BC,∴ . 如图13所示,过点E作EG∥AC,EG与边BC相交于点G. ∵ EF∥BC,EG∥AC, ∴ 四边形EGCF为平行四边形,∴ GC=EF, ∴ ,∴ 总结:平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形与原三角形的对应边成比例. 通过归纳总结,使学生掌握平行线分线段成比例的基本事实的推论,为解决此类问题打下理论基础. 熟记该基本事实及推论的几种基本图形有助于解该类题. 通过例1、例2加深平行线分线段成比例的基本事实的推论的理解.
3.学以致用,应用新知 考点1 平行线分线段成比例的基本事实 练习1 已知,AD是△ABC的中线,点E在AC上,BE交AD于点F.某数学兴趣小组在研究这个图形时得到如下结论: (1)当=时,=; (2)当=时,=; (3)当=时,=; …. 猜想:当 时,=?并说明理由. 【问题探索】 要求当时,的值为多少,我们可以通过作辅助线,利用平行线分线段成比例的基本事实,证得,得到EG=nAE,证明EG=CG,AC=(2n+1)AE,即可解决问题. 解:猜想:当=时,=. 理由如下: 如图14,过点D作DG∥BE,交AC于点G, 则==, ∴ =,EG=nAE. ∵ AD是△ABC的中线, ∴ 点D是BC的中点. 又∵ DG∥BE, ∴ EG=CG,AC=(2n+1)AE, ∴ =. 变式训练1 如图,已知AB∥CD∥EF,它们依次交直线l1,l2于点A,D,F和点B,C,E,如果AD=6,DF=3,BC=5,那么BE的值为( ) A.7.5 B.8.5 C.9 D.11 答案:A 通过作平行线,利用平行线分线段成比例的基本事实证明三角形中线段的比例,解题的关键是作辅助线,构造平行线,灵活运用平行线分线段成比例的基本事实来分析、判断、推理或解答.
4.随堂训练,巩固新知 1.如图15,已知l1∥l2∥l3,下列比例式成立的是( ) A. B. C. D. 图15 图16 答案:C 2.如图16,在△ABC中,点D,E分别在边AB,AC上,DE∥BC.已知AE=6,,则EC=( ) A.4.5 B.8 C.10.5 D.14 答案:B 3.如图17,BC∥DE,AB=15,AC=9,BD = 10,则AE=______. 图17 图18 答案:15 4.如图18,DE∥BC,AB=6,AC=9,AD=2,则EC=______. 答案:12 5.如图19,在△ABC中,DE∥BC,AC=4 ,AB=3,EC=1.求AD和BD的长. 解:∵ AC=4,EC=1,∴ AE=3. ∵ DE∥BC,∴ . ∴,∴ AD=, ∴ BD=3-=. 6.如图,在△ABC中,DE∥BC,EF∥AB,AD=2,BD=4,BC=8.求BF和CF的长. 解:∵ AD=2,BD=4,∴ AB=6. ∵ DE∥BC, ∴ . ∵ EF∥AB,∴, ∴,∴ BF=. ∴ CF=8-=. 知识的综合运用,通过本环节的学习,让学生巩固所学知识.
5.课堂小结,自我完善 1.平行线分线段成比例基本事实的推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例. 2.平行于三角形一边的直线的性质:平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形与原三角形的对应边成比例. 通过学生自我反思、小组交流、引导学生自主完成对本节重要知识技能和思想方法的小结.
6.布置作业 课本P67练习,习题A组,P68习题B组 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 25.2 平行线分线段成比例 第2课时 平行线分线段成比例的基本事实的推论 1.平行线分线段成比例的基本事实的推论 平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例. 2.平行于三角形一边的直线的性质 平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形与原三角形的对应边成比例. 提纲掣领,重点突出.
教后反思 在探索活动中,要增强学生发现问题、解决问题的意识和养成合作交流的习惯.进一步培养学生合情推理能力和初步逻辑推理意识. 反思,更进一步提升.
课题 第2课时 平行线分线段成比例的基本事实的推论 授课类型 新授课
授课人
教学内容 课本P65-68
教学目标 1.掌握平行线分线段成比例的基本事实的推论. 2.了解平行于三角形一边的直线的性质. 3.会用平行线分线段成比例的基本事实的推论解决相关的计算和证明问题.
教学重难点 重点:平行线分线段成比例的基本事实的推论及其应用. 难点:会用平行线分线段成比例的基本事实的推论解决相关的计算和证明问题.
教学准备 多媒体课件
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 【回顾复行线分线段成比例的基本事实: 两条直线被一组平行线所截,截得的对应线段成比例. 图9 符号语言: 若l1 ∥l2∥ l3 ,则. 回顾复习上节课所学内容,有助于本节课的学习.
2.实践探究,学习新知 【探究】 平行线分线段成比例的推论 如图10,直线a ∥b∥c ,分别交直线m,n于 A1,A2,A3,B1,B2,B3.过点A1作直线n的平行线,分别交直线b,c于点C2,C3.图中有哪些成比例线段? 图10 教师活动:计算与的值,你有什么发现? 学生活动:它们的值分别相等. 学生总结,教师点评. 推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例. 数学符号语言: ∵ DE∥BC, ∴ 或. 思考:你能总结平行线分线段成比例的基本事实及推论的模型吗? 熟悉该基本事实及推论的几种基本图形. 【例题】 例1 如图12,在△ABC中,E,F分别是AB和AC上的点,且 EF∥BC, (1)如果AE = 7, EB = 5, FC = 4,那么AF的长是多少? (2)如果AB = 10, AE=6,AF = 5,那么FC的长是多少? 【问题探索】根据平行线分线段成比例的推论列出比例式,即可求出AF,FC的长. 解:(1)∵ EF∥BC,∴ . ∵ AE=7,EB=5,FC=4, ∴ ,∴ AF=. (2)∵ EF∥BC,∴ . ∵ AB=10,AE=6,AF=5, ∴ ∴ , ∴ FC=AC-AF=. 例2 如图13所示,在△ABC中,EF∥BC,EF与两边AB,AC分别相交于点E,F. 求证:. 证明:∵ EF∥BC,∴ . 如图13所示,过点E作EG∥AC,EG与边BC相交于点G. ∵ EF∥BC,EG∥AC, ∴ 四边形EGCF为平行四边形,∴ GC=EF, ∴ ,∴ 总结:平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形与原三角形的对应边成比例. 通过归纳总结,使学生掌握平行线分线段成比例的基本事实的推论,为解决此类问题打下理论基础. 熟记该基本事实及推论的几种基本图形有助于解该类题. 通过例1、例2加深平行线分线段成比例的基本事实的推论的理解.
3.学以致用,应用新知 考点1 平行线分线段成比例的基本事实 练习1 已知,AD是△ABC的中线,点E在AC上,BE交AD于点F.某数学兴趣小组在研究这个图形时得到如下结论: (1)当=时,=; (2)当=时,=; (3)当=时,=; …. 猜想:当 时,=?并说明理由. 【问题探索】 要求当时,的值为多少,我们可以通过作辅助线,利用平行线分线段成比例的基本事实,证得,得到EG=nAE,证明EG=CG,AC=(2n+1)AE,即可解决问题. 解:猜想:当=时,=. 理由如下: 如图14,过点D作DG∥BE,交AC于点G, 则==, ∴ =,EG=nAE. ∵ AD是△ABC的中线, ∴ 点D是BC的中点. 又∵ DG∥BE, ∴ EG=CG,AC=(2n+1)AE, ∴ =. 变式训练1 如图,已知AB∥CD∥EF,它们依次交直线l1,l2于点A,D,F和点B,C,E,如果AD=6,DF=3,BC=5,那么BE的值为( ) A.7.5 B.8.5 C.9 D.11 答案:A 通过作平行线,利用平行线分线段成比例的基本事实证明三角形中线段的比例,解题的关键是作辅助线,构造平行线,灵活运用平行线分线段成比例的基本事实来分析、判断、推理或解答.
4.随堂训练,巩固新知 1.如图15,已知l1∥l2∥l3,下列比例式成立的是( ) A. B. C. D. 图15 图16 答案:C 2.如图16,在△ABC中,点D,E分别在边AB,AC上,DE∥BC.已知AE=6,,则EC=( ) A.4.5 B.8 C.10.5 D.14 答案:B 3.如图17,BC∥DE,AB=15,AC=9,BD = 10,则AE=______. 图17 图18 答案:15 4.如图18,DE∥BC,AB=6,AC=9,AD=2,则EC=______. 答案:12 5.如图19,在△ABC中,DE∥BC,AC=4 ,AB=3,EC=1.求AD和BD的长. 解:∵ AC=4,EC=1,∴ AE=3. ∵ DE∥BC,∴ . ∴,∴ AD=, ∴ BD=3-=. 6.如图,在△ABC中,DE∥BC,EF∥AB,AD=2,BD=4,BC=8.求BF和CF的长. 解:∵ AD=2,BD=4,∴ AB=6. ∵ DE∥BC, ∴ . ∵ EF∥AB,∴, ∴,∴ BF=. ∴ CF=8-=. 知识的综合运用,通过本环节的学习,让学生巩固所学知识.
5.课堂小结,自我完善 1.平行线分线段成比例基本事实的推论:平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例. 2.平行于三角形一边的直线的性质:平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形与原三角形的对应边成比例. 通过学生自我反思、小组交流、引导学生自主完成对本节重要知识技能和思想方法的小结.
6.布置作业 课本P67练习,习题A组,P68习题B组 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 25.2 平行线分线段成比例 第2课时 平行线分线段成比例的基本事实的推论 1.平行线分线段成比例的基本事实的推论 平行于三角形一边的直线截其他两边(或两边的延长线),所得的对应线段成比例. 2.平行于三角形一边的直线的性质 平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形与原三角形的对应边成比例. 提纲掣领,重点突出.
教后反思 在探索活动中,要增强学生发现问题、解决问题的意识和养成合作交流的习惯.进一步培养学生合情推理能力和初步逻辑推理意识. 反思,更进一步提升.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
