25.6相似三角形的应用(第1课时 利用相似三角形测内径和高度)教学设计(表格式)冀教版数学九年级上册
文档属性
| 名称 | 25.6相似三角形的应用(第1课时 利用相似三角形测内径和高度)教学设计(表格式)冀教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 411.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-20 08:02:38 | ||
图片预览


文档简介
25.6 相似三角形的应用
课题 第1课时 利用相似三角形测内径和高度 授课类型 新授课
授课人
教学内容 课本P88-90
教学目标 1.在测量旗杆、电视塔等的具体情境中进一步理解相似三角形的概念及性质; 2.积累数学操作活动经验,培养学生的问题意识,提高分析问题和解决问题的能力; 3.在解决实际问题的过程中,感受到数学活动充满着探索与创造的乐趣.
教学重难点 重点:能灵活应用相似三角形的性质解决有关实际问题. 难点:如何把实际问题转化为数学模型.
教学准备 多媒体课件
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 【复习回顾】 教师活动:相似三角形有哪些性质? 学生活动1:相似三角形的对应角相等、对应边成比例. 学生活动2:相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比. 学生活动3:相似三角形周长的比等于相似比. 学生活动4:相似三角形面积的比等于相似比的平方. 教师活动:相似三角形的这些性质有哪些应用呢?这节课继续研究. 教师抛出问题,激发学生思考,从而调动学生学习的积极性,为下面的学习奠定基础.
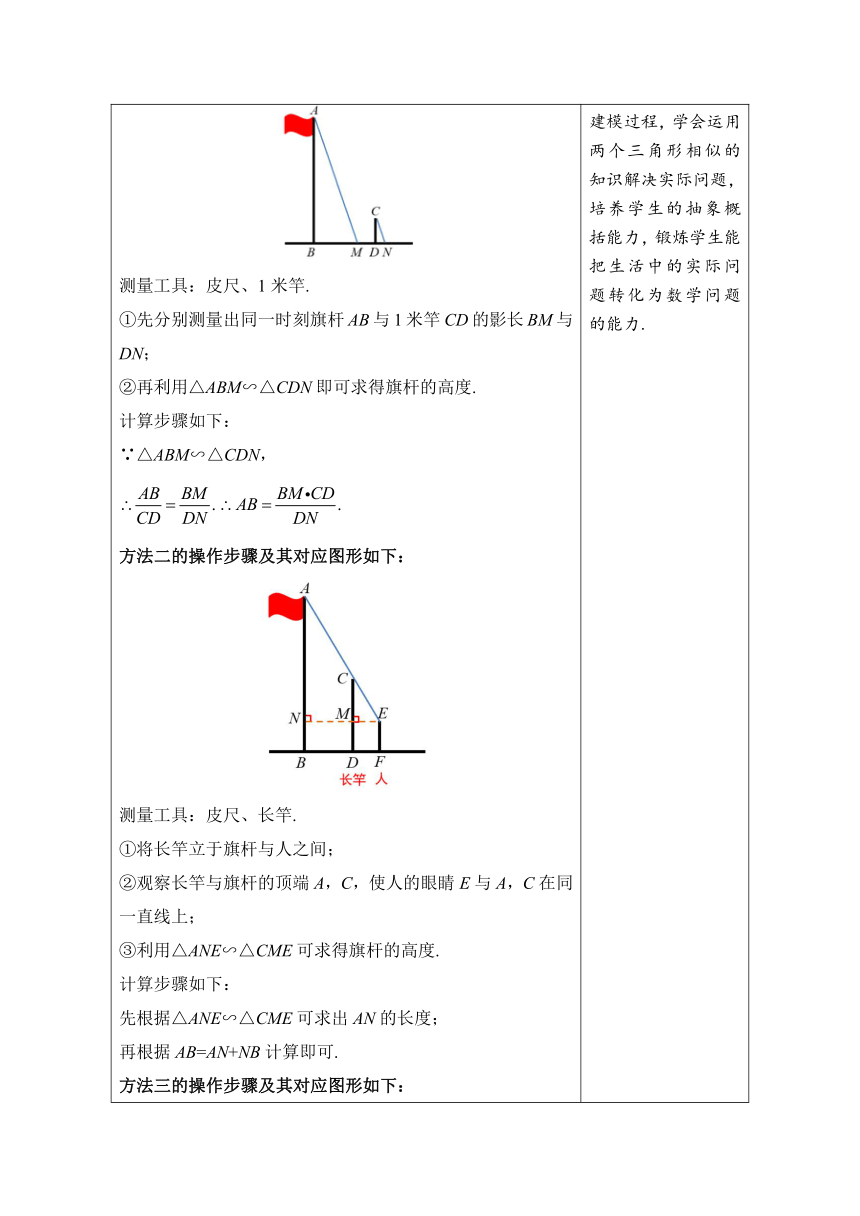
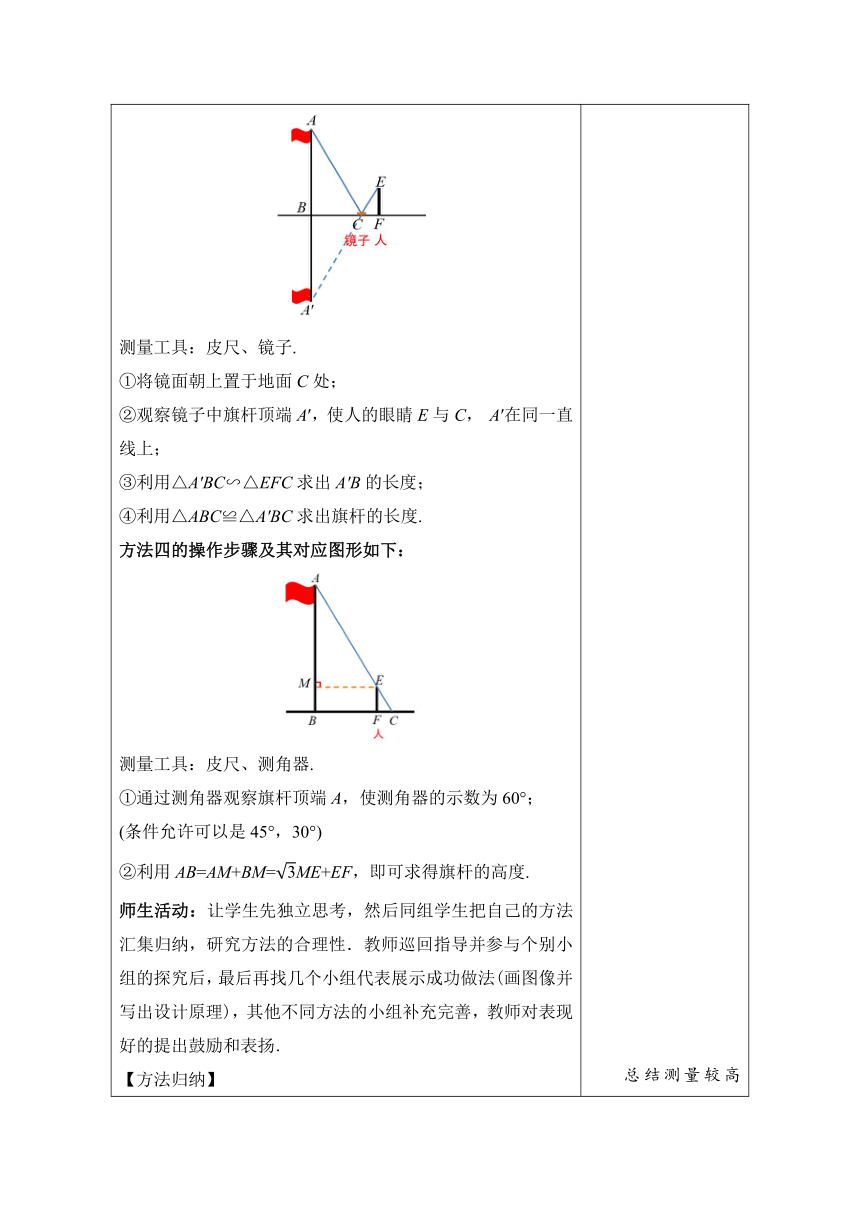
2.实践探究,学习新知 【探究1】利用相似三角形的性质测内径 学生活动:利用所学知识,设计测量空心圆柱形机械零件的内径的方案,并说明方案的可行性. 例1 这是一个零件的剖面图,外径为a,内径AB不能直接量出,求它的壁厚x,需要用交叉卡钳去量,如果OC:OA=OD:OB=1:m ,CD=b,请计算这个零件的壁厚x.(用含a,b,m的代数式表示) 解:∵,∠OCD=∠AOB, ∴△CDO~△ABO. ∴. 又∵CD=b, ∴AB=mb,x=. 即这个零件的内径为mb,壁厚为. 师生活动:小组合作探究,教师巡视,适当给予提示,小组展评. 【探究2】利用相似三角形的性质测量旗杆的高度 教师活动:提出问题:我们操场上飘扬的红旗,你想知道旗杆的高度吗?例1的做法给我们什么启发? 学生活动:测量旗杆的高度几种代表性的做法如下: 方法一的操作步骤及其对应图形如下: 测量工具:皮尺、1米竿. ①先分别测量出同一时刻旗杆AB与1米竿CD的影长BM与DN; ②再利用△ABM∽△CDN即可求得旗杆的高度. 计算步骤如下: ∵△ABM∽△CDN, 方法二的操作步骤及其对应图形如下: 测量工具:皮尺、长竿. ①将长竿立于旗杆与人之间; ②观察长竿与旗杆的顶端A,C,使人的眼睛E与A,C在同一直线上; ③利用△ANE∽△CME可求得旗杆的高度. 计算步骤如下: 先根据△ANE∽△CME可求出AN的长度; 再根据AB=AN+NB计算即可. 方法三的操作步骤及其对应图形如下: 测量工具:皮尺、镜子. ①将镜面朝上置于地面C处; ②观察镜子中旗杆顶端A′,使人的眼睛E与C, A′在同一直线上; ③利用△A′BC∽△EFC求出A′B的长度; ④利用△ABC≌△A′BC求出旗杆的长度. 方法四的操作步骤及其对应图形如下: 测量工具:皮尺、测角器. ①通过测角器观察旗杆顶端A,使测角器的示数为60°; (条件允许可以是45°,30°) ②利用AB=AM+BM=ME+EF,即可求得旗杆的高度. 师生活动:让学生先独立思考,然后同组学生把自己的方法汇集归纳,研究方法的合理性.教师巡回指导并参与个别小组的探究后,最后再找几个小组代表展示成功做法(画图像并写出设计原理),其他不同方法的小组补充完善,教师对表现好的提出鼓励和表扬. 【方法归纳】 测量高度的方法 测量较高的物体(很难到达顶部的物体)的高度,通常用“在同一时刻物体高与影长成正比例”的原理解决. 让学生动脑、动手,先设计方案,然后实施方案,真正让学生动起来,在活动的过程中培养学生的建模能力,在合作的过程中,培养学生的合作交流意识,积累数学活动经验. 让学生通过“审题→画示意图→明确数量关系→解决问题”的数学建模过程,学会运用两个三角形相似的知识解决实际问题,培养学生的抽象概括能力,锻炼学生能把生活中的实际问题转化为数学问题的能力. 总结测量较高物体高度的方法,培养学生的总结概括能力和语言表达能力.
3.学以致用,应用新知 考点1 利用相似三角形测内径 练习1 图1是装满红酒的高脚杯示意图,装酒的杯体可看作一个三角形,液面宽度为6cm,其它数据如图所示,喝掉一部分后的数据如图2所示,求此时液面宽度. 解:如图,过点O作OM⊥CD,垂足为M, 过点O′作O′N⊥AB,垂足为N, ∵AB∥CD, ∴△CDO~△ABO′, ∴, ∵OM=15-7=8 cm,O′N=11-7=4 cm, ∴, 解得:AB=3. 变式训练1 如图,用一个卡尺(AD=BC ,)测量气缸的内孔直径AB,量得CD的长为8 cm,则内孔直径AB的长为( ) A. cm B. cm C.28 cm D.20 cm 答案:D 考点2 利用标杆或阳光下的影子测高度 练习1 如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内.从标杆CD后退2米到点G处,在G处测得建筑物项端A、标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一直线上,求建筑物的高度. 解:设高为x米,根据题意易得△CDG∽△ABG, ∴. ∵CD=DG=2,∴BG=AB=x. 再由△EFH∽△ABH可得,即, ∴BH=2x, 即BD+DF+FH=2x,即x-2+52+4=2x, 解得x=54. 答:建筑物的高度为54米. 变式训练2 如图,某学生利用标杆测量一棵大树的高度,如果标杆EC的高为2 m,并测得BC=3 m,CA=1 m,那么树DB的高度是( ) A.6m B.8m C.32m D.0.125m 答案:B 巩固利用相似三角形测内径的方法,加深对所学知识的理解,提高学生知识的综合运用能力. 通过典型例题的分析,加深、巩固测量物体高度方法的使用,以及提高学生的解决问题的能力.
4.随堂训练,巩固新知 1.某校数学兴趣小组为测量学校旗杆AC的高度,在点F处竖立一根长为1.5米的标杆DF,如图(1)所示,量出DF的影子EF的长度为1米,再量出旗杆AC的影子BC的长度为6米,那么旗杆AC的高度为________米. 答案:9 2.如图,上体育课,甲、乙两名同学分别站在C,D的位置时,乙的影子恰好在甲的影子里边,已知甲、乙同学相距1米.甲身高1.8米,乙身高1.5米,则甲的影长是________米. 答案:6 3.如图,小明在A时测得某树的影长为2 m,B时又测得该树的影长为8 m,若两次日照的光线互相垂直,则树的高度为________m. 答案:4 4.一个圆柱形空心零件的上面有个孔,截面图如图所示,若OA:OD=OB:OC=,且量得AB=a,则厚度x可表示为( )
A. B. C. D. 答案:D 知识的综合运用,通过本环节的学习,让学生巩固所学知识.
5.课堂小结,自我完善 本节课所学知识: (1)测量物体的内径(无法直接测量的内径): 利用相似三角形对应边的比相等可测量物体的内径; (2)测高度: 在同一时刻物体高与影长成正比例; 通过学生自我反思,引导学生自主完成对本节重要知识技能和思想方法的小结.
6.布置作业 课本P89练习,P90习题 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 25.6 相似三角形的应用 第1课时 利用相似三角形测内径和高度 1.利用相似三角形测内径; 例题: 2.利用标杆或阳光下的影子测高度; 例题: 提纲掣领,重点突出.
教后反思 通过本节知识的学习,可以使学生综合运用三角形相似的判定和性质解决问题,发展学生的应用意识,加深学生对相似三角形的理解和认识.基本达到了预期的教学目标,大部分学生都学会了建立数学模型,利用相似的判定和性质来解决实际问题. 反思,更进一步提升.
课题 第1课时 利用相似三角形测内径和高度 授课类型 新授课
授课人
教学内容 课本P88-90
教学目标 1.在测量旗杆、电视塔等的具体情境中进一步理解相似三角形的概念及性质; 2.积累数学操作活动经验,培养学生的问题意识,提高分析问题和解决问题的能力; 3.在解决实际问题的过程中,感受到数学活动充满着探索与创造的乐趣.
教学重难点 重点:能灵活应用相似三角形的性质解决有关实际问题. 难点:如何把实际问题转化为数学模型.
教学准备 多媒体课件
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 【复习回顾】 教师活动:相似三角形有哪些性质? 学生活动1:相似三角形的对应角相等、对应边成比例. 学生活动2:相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比. 学生活动3:相似三角形周长的比等于相似比. 学生活动4:相似三角形面积的比等于相似比的平方. 教师活动:相似三角形的这些性质有哪些应用呢?这节课继续研究. 教师抛出问题,激发学生思考,从而调动学生学习的积极性,为下面的学习奠定基础.
2.实践探究,学习新知 【探究1】利用相似三角形的性质测内径 学生活动:利用所学知识,设计测量空心圆柱形机械零件的内径的方案,并说明方案的可行性. 例1 这是一个零件的剖面图,外径为a,内径AB不能直接量出,求它的壁厚x,需要用交叉卡钳去量,如果OC:OA=OD:OB=1:m ,CD=b,请计算这个零件的壁厚x.(用含a,b,m的代数式表示) 解:∵,∠OCD=∠AOB, ∴△CDO~△ABO. ∴. 又∵CD=b, ∴AB=mb,x=. 即这个零件的内径为mb,壁厚为. 师生活动:小组合作探究,教师巡视,适当给予提示,小组展评. 【探究2】利用相似三角形的性质测量旗杆的高度 教师活动:提出问题:我们操场上飘扬的红旗,你想知道旗杆的高度吗?例1的做法给我们什么启发? 学生活动:测量旗杆的高度几种代表性的做法如下: 方法一的操作步骤及其对应图形如下: 测量工具:皮尺、1米竿. ①先分别测量出同一时刻旗杆AB与1米竿CD的影长BM与DN; ②再利用△ABM∽△CDN即可求得旗杆的高度. 计算步骤如下: ∵△ABM∽△CDN, 方法二的操作步骤及其对应图形如下: 测量工具:皮尺、长竿. ①将长竿立于旗杆与人之间; ②观察长竿与旗杆的顶端A,C,使人的眼睛E与A,C在同一直线上; ③利用△ANE∽△CME可求得旗杆的高度. 计算步骤如下: 先根据△ANE∽△CME可求出AN的长度; 再根据AB=AN+NB计算即可. 方法三的操作步骤及其对应图形如下: 测量工具:皮尺、镜子. ①将镜面朝上置于地面C处; ②观察镜子中旗杆顶端A′,使人的眼睛E与C, A′在同一直线上; ③利用△A′BC∽△EFC求出A′B的长度; ④利用△ABC≌△A′BC求出旗杆的长度. 方法四的操作步骤及其对应图形如下: 测量工具:皮尺、测角器. ①通过测角器观察旗杆顶端A,使测角器的示数为60°; (条件允许可以是45°,30°) ②利用AB=AM+BM=ME+EF,即可求得旗杆的高度. 师生活动:让学生先独立思考,然后同组学生把自己的方法汇集归纳,研究方法的合理性.教师巡回指导并参与个别小组的探究后,最后再找几个小组代表展示成功做法(画图像并写出设计原理),其他不同方法的小组补充完善,教师对表现好的提出鼓励和表扬. 【方法归纳】 测量高度的方法 测量较高的物体(很难到达顶部的物体)的高度,通常用“在同一时刻物体高与影长成正比例”的原理解决. 让学生动脑、动手,先设计方案,然后实施方案,真正让学生动起来,在活动的过程中培养学生的建模能力,在合作的过程中,培养学生的合作交流意识,积累数学活动经验. 让学生通过“审题→画示意图→明确数量关系→解决问题”的数学建模过程,学会运用两个三角形相似的知识解决实际问题,培养学生的抽象概括能力,锻炼学生能把生活中的实际问题转化为数学问题的能力. 总结测量较高物体高度的方法,培养学生的总结概括能力和语言表达能力.
3.学以致用,应用新知 考点1 利用相似三角形测内径 练习1 图1是装满红酒的高脚杯示意图,装酒的杯体可看作一个三角形,液面宽度为6cm,其它数据如图所示,喝掉一部分后的数据如图2所示,求此时液面宽度. 解:如图,过点O作OM⊥CD,垂足为M, 过点O′作O′N⊥AB,垂足为N, ∵AB∥CD, ∴△CDO~△ABO′, ∴, ∵OM=15-7=8 cm,O′N=11-7=4 cm, ∴, 解得:AB=3. 变式训练1 如图,用一个卡尺(AD=BC ,)测量气缸的内孔直径AB,量得CD的长为8 cm,则内孔直径AB的长为( ) A. cm B. cm C.28 cm D.20 cm 答案:D 考点2 利用标杆或阳光下的影子测高度 练习1 如图,某水平地面上建筑物的高度为AB,在点D和点F处分别竖立高是2米的标杆CD和EF,两标杆相隔52米,并且建筑物AB、标杆CD和EF在同一竖直平面内.从标杆CD后退2米到点G处,在G处测得建筑物项端A、标杆顶端C在同一条直线上;从标杆FE后退4米到点H处,在H处测得建筑物顶端A和标杆顶端E在同一直线上,求建筑物的高度. 解:设高为x米,根据题意易得△CDG∽△ABG, ∴. ∵CD=DG=2,∴BG=AB=x. 再由△EFH∽△ABH可得,即, ∴BH=2x, 即BD+DF+FH=2x,即x-2+52+4=2x, 解得x=54. 答:建筑物的高度为54米. 变式训练2 如图,某学生利用标杆测量一棵大树的高度,如果标杆EC的高为2 m,并测得BC=3 m,CA=1 m,那么树DB的高度是( ) A.6m B.8m C.32m D.0.125m 答案:B 巩固利用相似三角形测内径的方法,加深对所学知识的理解,提高学生知识的综合运用能力. 通过典型例题的分析,加深、巩固测量物体高度方法的使用,以及提高学生的解决问题的能力.
4.随堂训练,巩固新知 1.某校数学兴趣小组为测量学校旗杆AC的高度,在点F处竖立一根长为1.5米的标杆DF,如图(1)所示,量出DF的影子EF的长度为1米,再量出旗杆AC的影子BC的长度为6米,那么旗杆AC的高度为________米. 答案:9 2.如图,上体育课,甲、乙两名同学分别站在C,D的位置时,乙的影子恰好在甲的影子里边,已知甲、乙同学相距1米.甲身高1.8米,乙身高1.5米,则甲的影长是________米. 答案:6 3.如图,小明在A时测得某树的影长为2 m,B时又测得该树的影长为8 m,若两次日照的光线互相垂直,则树的高度为________m. 答案:4 4.一个圆柱形空心零件的上面有个孔,截面图如图所示,若OA:OD=OB:OC=,且量得AB=a,则厚度x可表示为( )
A. B. C. D. 答案:D 知识的综合运用,通过本环节的学习,让学生巩固所学知识.
5.课堂小结,自我完善 本节课所学知识: (1)测量物体的内径(无法直接测量的内径): 利用相似三角形对应边的比相等可测量物体的内径; (2)测高度: 在同一时刻物体高与影长成正比例; 通过学生自我反思,引导学生自主完成对本节重要知识技能和思想方法的小结.
6.布置作业 课本P89练习,P90习题 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 25.6 相似三角形的应用 第1课时 利用相似三角形测内径和高度 1.利用相似三角形测内径; 例题: 2.利用标杆或阳光下的影子测高度; 例题: 提纲掣领,重点突出.
教后反思 通过本节知识的学习,可以使学生综合运用三角形相似的判定和性质解决问题,发展学生的应用意识,加深学生对相似三角形的理解和认识.基本达到了预期的教学目标,大部分学生都学会了建立数学模型,利用相似的判定和性质来解决实际问题. 反思,更进一步提升.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
