25.6相似三角形的应用(第2课时 利用相似三角形的性质测量距离) 教学设计(表格式)冀教版数学九年级上册
文档属性
| 名称 | 25.6相似三角形的应用(第2课时 利用相似三角形的性质测量距离) 教学设计(表格式)冀教版数学九年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 161.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-20 08:11:38 | ||
图片预览


文档简介
25.6 相似三角形的应用
课题 第2课时 利用相似三角形测距离 授课类型 新授课
授课人
教学内容 课本P90-92
教学目标 1.能够利用相似三角形的知识,求出不能直接测量的物体的宽度和距离,培养学生的建模能力,增强学生的核心素养. 2.通过利用相似的性质解决实际问题,培养学生的几何直观与推理能力,发展学生的应用意识. 3.通过小组合作解决实际问题,培养学生的动手操作能力和交流与合作的意识,积累活动经验,增强核心素养.
教学重难点 重点:利用相似三角形的性质求不能直接测量的距离. 难点:将实际问题抽象成数学问题.
教学准备 多媒体课件
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 如图,是一条河,直接测量河的宽度不太容易操作,你还记得如何用相似三角形的知识测量旗杆的高度?像测量旗杆的高度一样,一些不能直接测量的物体的长度或高度,我们可以借助于相似三角形的知识解决. 这节课我们来说测量一下河的宽度. 教师抛出问题,激发学生思考,从而调动学生学习的积极性,为下面的学习奠定基础.
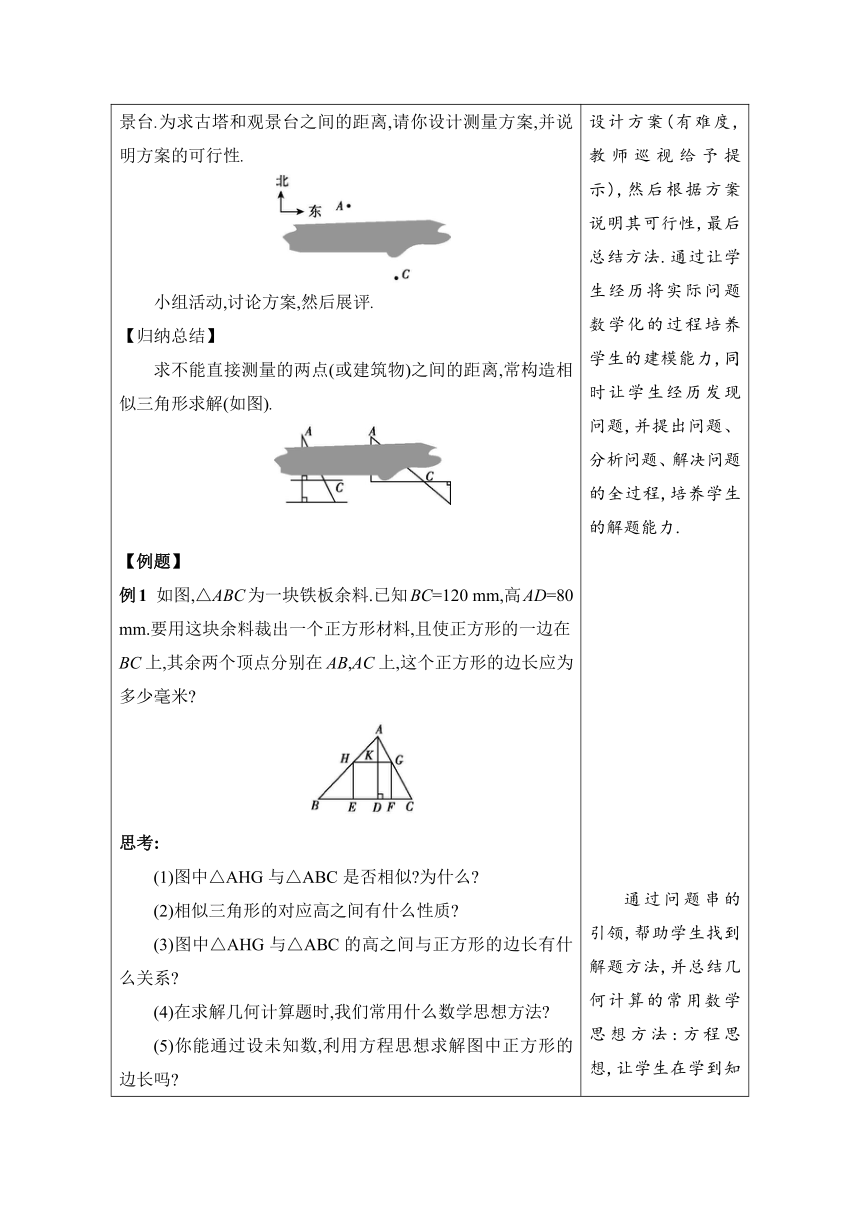
2.实践探究,学习新知 【探究】 如图,在一条小河的北岸A处有一古塔,南岸C处有一观景台.为求古塔和观景台之间的距离,请你设计测量方案,并说明方案的可行性. 小组活动,讨论方案,然后展评. 【归纳总结】 求不能直接测量的两点(或建筑物)之间的距离,常构造相似三角形求解(如图). 【例题】 例1 如图,△ABC为一块铁板余料.已知BC=120 mm,高AD=80 mm.要用这块余料裁出一个正方形材料,且使正方形的一边在BC上,其余两个顶点分别在AB,AC上,这个正方形的边长应为多少毫米 思考: (1)图中△AHG与△ABC是否相似 为什么 (2)相似三角形的对应高之间有什么性质 (3)图中△AHG与△ABC的高之间与正方形的边长有什么关系 (4)在求解几何计算题时,我们常用什么数学思想方法 (5)你能通过设未知数,利用方程思想求解图中正方形的边长吗 师生活动:小组合作探究,教师巡视,适当给予提示,小组展评. 解:设裁出的正方形为EFGH,△ABC的高AD与HG交于点K,则AK为△AHG的高. ∵HG∥EF, ∴∠AHG=∠B. 又∵∠BAC为公共角, ∴△AHG∽△ABC. ∴=. ∵四边形EFGH为正方形, ∴AK=AD-HG. ∴=. 设HG=x mm,则=. 解得x=48. 答:裁出的正方形的边长为48 mm. 思考:若上题条件不变,将正方形改为长方形,且HG=2HE,你能求这个长方形的边长吗 试一试. 引导学生想办法求河两岸两点之间的距离,先让学生设计方案(有难度,教师巡视给予提示),然后根据方案说明其可行性,最后总结方法.通过让学生经历将实际问题数学化的过程培养学生的建模能力,同时让学生经历发现问题,并提出问题、分析问题、解决问题的全过程,培养学生的解题能力. 通过问题串的引领,帮助学生找到解题方法,并总结几何计算的常用数学思想方法:方程思想,让学生在学到知识的同时学到数学思想方法.通过问题的变式,将此类题变式提升,培养学生类比解题的能力.
3.学以致用,应用新知 考点1 测河宽 练习1 如图,为了测量一池塘的宽DE,在岸边找一点C,连接CD,CE,测得CD=30 m,在DC的延长线上找一点A,测得AC=5 m,过点A作AB∥DE,交EC的延长线于B,测得AB=6 m,求池塘的宽DE. 解:∵AB⊥DE, ∴△ABC~△DEC, ∴, ∴, 解得DE=36(m). 答:池塘的宽为36 m. 变式训练1 如图,为了估计河的宽度,我们可以在河对岸选定一个目标点A,在近岸取点B,使AB与河岸垂直,在近岸取点C,E,使BC⊥AB,CE⊥BC,AE与BC交于点D.已测得BD=40 m,DC=20 m,EC=24 m,则河宽AB为______. 答案:48 m 考点2 三角形内接矩形 练习2 有一块三角形余料ABC,它的边BC=100 mm,高AD=60 mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点P,N分别在AB,AC上,求加工成的正方形零件的边长. 解:∵正方形边长QM在BC上, ∴PN∥BC, ∵AD⊥BC, ∴AE⊥PN, ∴△APN~△ABC, ∴, 设ED=x, 则PN=MN=ED=x, ∴, ∴x=37.5 mm, ∴加工成的正方形零件的边长为37.5 mm. 变式训练2 清朝《数理精蕴》里有一首小诗《古色古香方城池》:今有一座古方城,四面正中都开门,南门直行八里止,脚下有座塔耸立.又出西门二里停,切城角恰见塔形,请问诸君能算者,方城每边长是几?如图所示,诗的意思是:有正方形的城池一座,四面城墙的正中有门,从南门口(点)直行8里有一塔(点),自西门(点)直行2里至点,切城角(点)也可以看见塔,问这座方城每面城墙的长是 ________里. 答案:8 巩固利用相似三角形求河宽的方法,加深对所学知识的理解,提高学生知识的综合运用能力. 巩固利用相似三角形求内接矩形的方法,加深对所学知识的理解,提高学生知识的综合运用能力.
4.随堂训练,巩固新知 1.《九章算术》是我国古代的数学名著,书中有这样一个问题:“今有邑方不知大小,各中开门,出北门一百步立一表,出西门二百二十五步适可见之,问邑方几何 ”它的意思是:如图,分别是正方形的边的中点,,,过点,且步,步, 那么该正方形城邑边长约为( )步 A.300 B.260 C.225 D.185 答案:A 2.如图,△ABC是一块锐角三角形材料,高线AH长8 cm,底边BC长10 cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D,G分别在AB,AC上,则四边形DEFG的最大面积为( ) A.40 cm2 B.20 cm2 C.25 cm2 D.10 cm2 答案:B 3.如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边15米的P点处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为________米. 答案:22.5 知识的综合运用,通过本环节的学习,让学生巩固所学知识.
5.课堂小结,自我完善 本节课我们研究了相似三角形在实际生活中的应用,请同学们带着以下问题进行总结: (1)本节课你学到了哪些知识 目前为止利用相似三角形的知识可以解决哪些问题 (2)本节课学习经历了怎样的过程 这个过程中用到了哪些数学方法 积累了哪些活动经验 通过反思数学思想方法与活动经验,培养学生的数学思维品质,让学生学会学习,学会思考.
6.布置作业 课本P92习题 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 25.6 相似三角形的应用 第2课时 利用相似三角形测距离 提纲掣领,重点突出.
教后反思 相似应用最广泛的是测量学中的应用,在实际测量物体的高度、宽度时,关键是要构造和实物所在三角形相似的三角形,而且要能测量已知三角形的各条线段的长,运用相似三角形的性质列出比例式求解.会构造与实物相似的三角形,通过对实际问题的分析和解决,让学生充分感受到数学与现实世界的联系,最大限度地调动学生学习的积极性和主动性. 反思,更进一步提升.
课题 第2课时 利用相似三角形测距离 授课类型 新授课
授课人
教学内容 课本P90-92
教学目标 1.能够利用相似三角形的知识,求出不能直接测量的物体的宽度和距离,培养学生的建模能力,增强学生的核心素养. 2.通过利用相似的性质解决实际问题,培养学生的几何直观与推理能力,发展学生的应用意识. 3.通过小组合作解决实际问题,培养学生的动手操作能力和交流与合作的意识,积累活动经验,增强核心素养.
教学重难点 重点:利用相似三角形的性质求不能直接测量的距离. 难点:将实际问题抽象成数学问题.
教学准备 多媒体课件
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 如图,是一条河,直接测量河的宽度不太容易操作,你还记得如何用相似三角形的知识测量旗杆的高度?像测量旗杆的高度一样,一些不能直接测量的物体的长度或高度,我们可以借助于相似三角形的知识解决. 这节课我们来说测量一下河的宽度. 教师抛出问题,激发学生思考,从而调动学生学习的积极性,为下面的学习奠定基础.
2.实践探究,学习新知 【探究】 如图,在一条小河的北岸A处有一古塔,南岸C处有一观景台.为求古塔和观景台之间的距离,请你设计测量方案,并说明方案的可行性. 小组活动,讨论方案,然后展评. 【归纳总结】 求不能直接测量的两点(或建筑物)之间的距离,常构造相似三角形求解(如图). 【例题】 例1 如图,△ABC为一块铁板余料.已知BC=120 mm,高AD=80 mm.要用这块余料裁出一个正方形材料,且使正方形的一边在BC上,其余两个顶点分别在AB,AC上,这个正方形的边长应为多少毫米 思考: (1)图中△AHG与△ABC是否相似 为什么 (2)相似三角形的对应高之间有什么性质 (3)图中△AHG与△ABC的高之间与正方形的边长有什么关系 (4)在求解几何计算题时,我们常用什么数学思想方法 (5)你能通过设未知数,利用方程思想求解图中正方形的边长吗 师生活动:小组合作探究,教师巡视,适当给予提示,小组展评. 解:设裁出的正方形为EFGH,△ABC的高AD与HG交于点K,则AK为△AHG的高. ∵HG∥EF, ∴∠AHG=∠B. 又∵∠BAC为公共角, ∴△AHG∽△ABC. ∴=. ∵四边形EFGH为正方形, ∴AK=AD-HG. ∴=. 设HG=x mm,则=. 解得x=48. 答:裁出的正方形的边长为48 mm. 思考:若上题条件不变,将正方形改为长方形,且HG=2HE,你能求这个长方形的边长吗 试一试. 引导学生想办法求河两岸两点之间的距离,先让学生设计方案(有难度,教师巡视给予提示),然后根据方案说明其可行性,最后总结方法.通过让学生经历将实际问题数学化的过程培养学生的建模能力,同时让学生经历发现问题,并提出问题、分析问题、解决问题的全过程,培养学生的解题能力. 通过问题串的引领,帮助学生找到解题方法,并总结几何计算的常用数学思想方法:方程思想,让学生在学到知识的同时学到数学思想方法.通过问题的变式,将此类题变式提升,培养学生类比解题的能力.
3.学以致用,应用新知 考点1 测河宽 练习1 如图,为了测量一池塘的宽DE,在岸边找一点C,连接CD,CE,测得CD=30 m,在DC的延长线上找一点A,测得AC=5 m,过点A作AB∥DE,交EC的延长线于B,测得AB=6 m,求池塘的宽DE. 解:∵AB⊥DE, ∴△ABC~△DEC, ∴, ∴, 解得DE=36(m). 答:池塘的宽为36 m. 变式训练1 如图,为了估计河的宽度,我们可以在河对岸选定一个目标点A,在近岸取点B,使AB与河岸垂直,在近岸取点C,E,使BC⊥AB,CE⊥BC,AE与BC交于点D.已测得BD=40 m,DC=20 m,EC=24 m,则河宽AB为______. 答案:48 m 考点2 三角形内接矩形 练习2 有一块三角形余料ABC,它的边BC=100 mm,高AD=60 mm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点P,N分别在AB,AC上,求加工成的正方形零件的边长. 解:∵正方形边长QM在BC上, ∴PN∥BC, ∵AD⊥BC, ∴AE⊥PN, ∴△APN~△ABC, ∴, 设ED=x, 则PN=MN=ED=x, ∴, ∴x=37.5 mm, ∴加工成的正方形零件的边长为37.5 mm. 变式训练2 清朝《数理精蕴》里有一首小诗《古色古香方城池》:今有一座古方城,四面正中都开门,南门直行八里止,脚下有座塔耸立.又出西门二里停,切城角恰见塔形,请问诸君能算者,方城每边长是几?如图所示,诗的意思是:有正方形的城池一座,四面城墙的正中有门,从南门口(点)直行8里有一塔(点),自西门(点)直行2里至点,切城角(点)也可以看见塔,问这座方城每面城墙的长是 ________里. 答案:8 巩固利用相似三角形求河宽的方法,加深对所学知识的理解,提高学生知识的综合运用能力. 巩固利用相似三角形求内接矩形的方法,加深对所学知识的理解,提高学生知识的综合运用能力.
4.随堂训练,巩固新知 1.《九章算术》是我国古代的数学名著,书中有这样一个问题:“今有邑方不知大小,各中开门,出北门一百步立一表,出西门二百二十五步适可见之,问邑方几何 ”它的意思是:如图,分别是正方形的边的中点,,,过点,且步,步, 那么该正方形城邑边长约为( )步 A.300 B.260 C.225 D.185 答案:A 2.如图,△ABC是一块锐角三角形材料,高线AH长8 cm,底边BC长10 cm,要把它加工成一个矩形零件,使矩形DEFG的一边EF在BC上,其余两个顶点D,G分别在AB,AC上,则四边形DEFG的最大面积为( ) A.40 cm2 B.20 cm2 C.25 cm2 D.10 cm2 答案:B 3.如图,一条河的两岸有一段是平行的,在河的南岸边每隔5米有一棵树,在北岸边每隔50米有一根电线杆.小丽站在离南岸边15米的P点处看北岸,发现北岸相邻的两根电线杆恰好被南岸的两棵树遮住,并且在这两棵树之间还有三棵树,则河宽为________米. 答案:22.5 知识的综合运用,通过本环节的学习,让学生巩固所学知识.
5.课堂小结,自我完善 本节课我们研究了相似三角形在实际生活中的应用,请同学们带着以下问题进行总结: (1)本节课你学到了哪些知识 目前为止利用相似三角形的知识可以解决哪些问题 (2)本节课学习经历了怎样的过程 这个过程中用到了哪些数学方法 积累了哪些活动经验 通过反思数学思想方法与活动经验,培养学生的数学思维品质,让学生学会学习,学会思考.
6.布置作业 课本P92习题 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 25.6 相似三角形的应用 第2课时 利用相似三角形测距离 提纲掣领,重点突出.
教后反思 相似应用最广泛的是测量学中的应用,在实际测量物体的高度、宽度时,关键是要构造和实物所在三角形相似的三角形,而且要能测量已知三角形的各条线段的长,运用相似三角形的性质列出比例式求解.会构造与实物相似的三角形,通过对实际问题的分析和解决,让学生充分感受到数学与现实世界的联系,最大限度地调动学生学习的积极性和主动性. 反思,更进一步提升.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
