25.7相似多边形和图形的位似(第1课时 相似多边形) 教学设计(表格式)冀教版数学九年级上册
文档属性
| 名称 | 25.7相似多边形和图形的位似(第1课时 相似多边形) 教学设计(表格式)冀教版数学九年级上册 |
|
|
| 格式 | docx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-20 00:00:00 | ||
图片预览




文档简介
25.7 相似多边形和图形的位似
课题 第1课时 相似多边形 授课类型 新授课
授课人
教学内容 课本P93-96
教学目标 1.从生活中形状相同的图形的实例中认识相似图形. 2.理解相似多边形及相似多边形的性质,并会应用性质解决问题.
教学重难点 重点:相似多边形的判定. 难点:两个多边形相似性质的简单应用.
教学准备 多媒体课件
教与学互动设计(教学过程) 设计意图
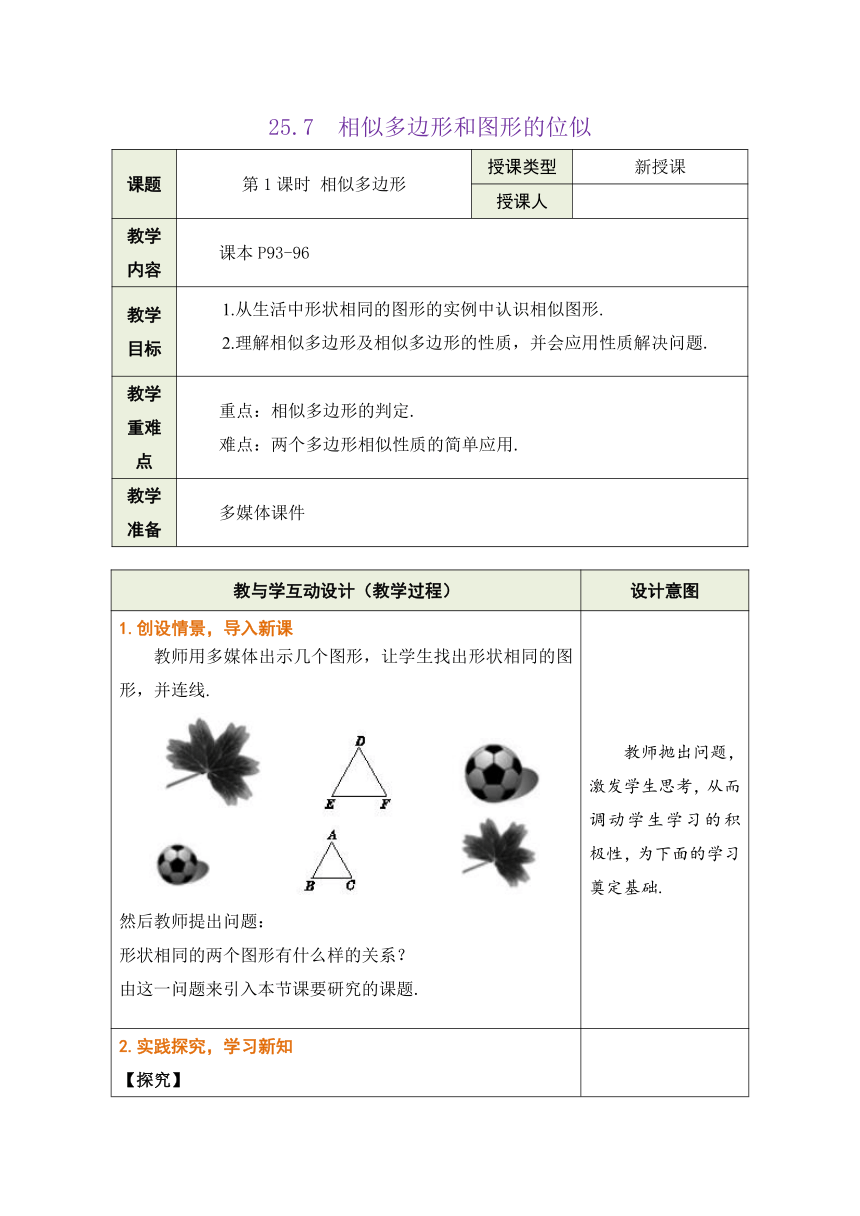
1.创设情景,导入新课 教师用多媒体出示几个图形,让学生找出形状相同的图形,并连线. 然后教师提出问题: 形状相同的两个图形有什么样的关系? 由这一问题来引入本节课要研究的课题. 教师抛出问题,激发学生思考,从而调动学生学习的积极性,为下面的学习奠定基础.
2.实践探究,学习新知 【探究】 1.相似图形 问题1:观察上面的图片,你能发现它们有什么特点吗 学生活动:形状相同,大小不一定相同. 问题2:两个相似图形之间有什么关系呢? 归纳:两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到的. 【思考】 全等图形一定是相似图形吗 相似图形一定全等吗 它们之间有什么关系 学生活动:小组交流,教师引导. 结论:全等图形是相似图形的一种特殊情况.全等图形一定相似,相似图形不一定全等. 2.相似多边形 图1中的两个多边形分别是幻灯片上的多边形ABCDEF和银幕上的多边形A1B1C1D1E1F1. 图 1 教师活动:它们的形状相同吗? 学生活动:六边形ABCDEF和六边形A1B1C1D1E1F1形状相同. 教师活动:在上面的两个多边形中,是否有相等的内角?设法验证你的猜测. 学生活动:∠A与∠A1,∠B与B1,∠C与∠C1,∠D与∠D1,∠E与∠E1,∠F与∠F1分别对应相等. 教师活动:这样的角我们称为对应角,在上面的两个多边形中,夹相等内角的两边是否成比例? 学生活动:通过测量,AB与A1B1,BC与B1C1,CD与C1D1,DE与D1E1,EF与E1F1,FA与F1A1的比相等. 教师活动:这样的边我们称为对应边. 教师活动:从上面的讨论结果来看,大家能否猜到相似多边形的定义呢? 学生活动:可以,一般地,如果两个多边形的对应角相等、对应边成比例,那么这两个多边形叫做相似多边形.相似多边形对应边的比叫做它们的相似比. 教师活动:相似怎样表示呢?请同学们认真看书. 学生活动:六边形ABCDEF和六边形A1B1C1D1E1F1相似,记作六边形ABCDEF∽六边形A1B1C1D1E1F1. 教师活动:相似多边形对应边的比叫做相似比,一般用字母k表示,“∽”读作“相似于”.在记两个多边形相似时,需要注意什么? 学生活动:要把表示对应顶点的字母写在对应的位置上. 几何语言:如图2所示的两个大小不同的四边形ABCD和四边形A1B1C1D1中,∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1,,因此四边形ABCD与四边形A1B1C1D1相似. 图 2 教师活动:通过对相似多边形概念的理解,相似多边形具有哪些性质呢? 学生活动:相似多边形的性质:相似多边形的对应角相等,对应边成比例. 【观察与思考】 分别观察图3(1)和(2)中的两个多边形,先直观判断它们是不是相似多边形,再经过测量与计算,验证你的结论. (1) (2) 图 3 学生活动:小组探究需要做什么,并交流结果. 分别求出这两个四边形的对应边的长度,并分别量出这两个四边形各个内角的度数. 结论:均是相似多边形. 【例题】 例1 如图4所示,五边形ABCDE∽五边形A1B1C1D1E1,求C1D1的长和∠A的度数. 图4 【问题探索】 (1)相似多边形的性质是什么? (2)相似五边形中,对应边AB与A1B1,CD与C1D1之间有什么关系? (3)在比例式中,已知三条线段的长能否求出第四条线段的长?尝试求出C1D1的长. (4)根据相似多边形的性质,你能求出∠E的大小吗? (5)五边形的内角和是多少度? (6)由五边形内角和定理,能否求出∠A的值? 解:∵ 五边形ABCDE∽五边形A1B1C1D1E1, ∴ ,∠E=∠E1=145°. ∵ AB=15,A1B1=10,CD=21, ∴ ,解得C1D1=14. 又∵ ∠B=130°,∠C=∠D=90°, ∴ ∠A=(5-2)×180°-130°-145°-2×90°=85°. ∴ C1D1=14,∠A=85°. 把分析问题的过程设置成小问题的形式,通过教师的引导或者小组合作交流,学生层层递进的方式分析并解决问题,降低了学习难度,进一步培养学生分析问题的能力. 通过问题的形式教师逐步引导学生了解相似多边形的各个性质. 通过以上问题得出的结论,推导出图3中均是相似多边形. 通过例题,让学生掌握相似多边形的各个性质.
3.学以致用,应用新知 考点1 相似多边形的性质 练习1 如图,四边形ABCD~四边形A1B1C1D1,∠A=116°,∠B=40°,∠C=65°,求x的值和∠D1的度数.
解:∵∠A=116°,∠B=40°,∠C=65°, ∴∠D=360°-116°-40°-65°=139°. ∵四边形ABCD~四边形A1B1C1D1, ∴∠D1=∠D=139°,. ∴, ∴x=. 变式训练1 如图,平行四边形ABCD∽平行四边形AEFB,且AB=3 cm,BC=6 cm.求AE的长. 解:∵ 平行四边形ABCD∽平行四边形AEFB, ∴ . 又∵ AB=3 cm,BC=6 cm,EF=AB=3 cm, ∴ AE=(cm). 巩固相似多边形的性质,加深对所学知识的理解,提高学生知识的综合运用能力.
4.随堂训练,巩固新知 1.放大镜中的多边形与原多边形的关系是( ) A.形状不同,大小不同 B.形状相同,大小相同 C.形状相同,大小不同 D.形状不同,大小相同 答案:C 2.给出下列命题:①所有的正方形都相似;②所有的矩形都相似;③所有的三角形都相似;④所有的等腰直角三角形都相似;⑤所有的正五边形都相似.其中,正确命题为 ( ) A.①②③ B.①③⑤ C.①④⑤ D.②④⑤ 答案:C 3.在矩形ABCD中,AB=4,BC=3,下列四个矩形中与矩形ABCD相似的是( ) A B C D 4.若△ABC∽△A′B′C′,且AB︰A′B′=1∶2,则△ABC与△A′B′C′相似比是 ,△A′B′C′与△ABC的相似比是 . 答案: 2 5.如图所示,六边形ABCDEF与六边形A'B'C'D'E'F'相似,已知AB=5 cm,EF=6 cm,CD与C'D'的比为1∶3,∠E=125°,求A'B',E'F'的长及∠E'的度数. 解:∵ 六边形ABCDEF与六边形A'B'C'D'E'F'相似, ∴ ,∠E′=∠E=125°. ∴ A'B'=3AB=15 cm,E'F'=3EF=18 cm. 6.如图所示的两个矩形相似吗?为什么? 解:矩形ABCD ∽ 矩形EFGH, 因为它们的对应角相等,对应边的比也相等. 知识的综合运用,通过本环节的学习,让学生巩固所学知识.
5.课堂小结,自我完善 本节课所学知识: 1.相似图形的概念 2.相似多边形的定义 3.相似多边形的性质 4.相似比的定义 通过学生自我反思、小组交流、引导学生自主完成对本节重要知识技能和思想方法的小结.
6.布置作业 课本P95习题A组,B组 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 25.7 相似多边形和图形的位似 第1课时 相似多边形 1.相似图形: (1)概念:我们把形状相同的图形叫做相似图形. 2.相似多边形 (1)定义:一般地,如果两个多边形的对应角相等、对应边成比例,那么这两个多边形叫做相似多边形. (2)性质:对应角相等;对应边成比例. 3.相似比 (1)定义:相似多边形对应边的比叫做相似比. 提纲掣领,重点突出.
教后反思 本节课主要是相似多边形的定义,这节课主要是让学生自学,将定义和相似比等概念进行理解记忆,通过与相似三角形的定义的对比,得到相似多边形的相关概念. 反思,更进一步提升.
课题 第1课时 相似多边形 授课类型 新授课
授课人
教学内容 课本P93-96
教学目标 1.从生活中形状相同的图形的实例中认识相似图形. 2.理解相似多边形及相似多边形的性质,并会应用性质解决问题.
教学重难点 重点:相似多边形的判定. 难点:两个多边形相似性质的简单应用.
教学准备 多媒体课件
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 教师用多媒体出示几个图形,让学生找出形状相同的图形,并连线. 然后教师提出问题: 形状相同的两个图形有什么样的关系? 由这一问题来引入本节课要研究的课题. 教师抛出问题,激发学生思考,从而调动学生学习的积极性,为下面的学习奠定基础.
2.实践探究,学习新知 【探究】 1.相似图形 问题1:观察上面的图片,你能发现它们有什么特点吗 学生活动:形状相同,大小不一定相同. 问题2:两个相似图形之间有什么关系呢? 归纳:两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到的. 【思考】 全等图形一定是相似图形吗 相似图形一定全等吗 它们之间有什么关系 学生活动:小组交流,教师引导. 结论:全等图形是相似图形的一种特殊情况.全等图形一定相似,相似图形不一定全等. 2.相似多边形 图1中的两个多边形分别是幻灯片上的多边形ABCDEF和银幕上的多边形A1B1C1D1E1F1. 图 1 教师活动:它们的形状相同吗? 学生活动:六边形ABCDEF和六边形A1B1C1D1E1F1形状相同. 教师活动:在上面的两个多边形中,是否有相等的内角?设法验证你的猜测. 学生活动:∠A与∠A1,∠B与B1,∠C与∠C1,∠D与∠D1,∠E与∠E1,∠F与∠F1分别对应相等. 教师活动:这样的角我们称为对应角,在上面的两个多边形中,夹相等内角的两边是否成比例? 学生活动:通过测量,AB与A1B1,BC与B1C1,CD与C1D1,DE与D1E1,EF与E1F1,FA与F1A1的比相等. 教师活动:这样的边我们称为对应边. 教师活动:从上面的讨论结果来看,大家能否猜到相似多边形的定义呢? 学生活动:可以,一般地,如果两个多边形的对应角相等、对应边成比例,那么这两个多边形叫做相似多边形.相似多边形对应边的比叫做它们的相似比. 教师活动:相似怎样表示呢?请同学们认真看书. 学生活动:六边形ABCDEF和六边形A1B1C1D1E1F1相似,记作六边形ABCDEF∽六边形A1B1C1D1E1F1. 教师活动:相似多边形对应边的比叫做相似比,一般用字母k表示,“∽”读作“相似于”.在记两个多边形相似时,需要注意什么? 学生活动:要把表示对应顶点的字母写在对应的位置上. 几何语言:如图2所示的两个大小不同的四边形ABCD和四边形A1B1C1D1中,∠A=∠A1,∠B=∠B1,∠C=∠C1,∠D=∠D1,,因此四边形ABCD与四边形A1B1C1D1相似. 图 2 教师活动:通过对相似多边形概念的理解,相似多边形具有哪些性质呢? 学生活动:相似多边形的性质:相似多边形的对应角相等,对应边成比例. 【观察与思考】 分别观察图3(1)和(2)中的两个多边形,先直观判断它们是不是相似多边形,再经过测量与计算,验证你的结论. (1) (2) 图 3 学生活动:小组探究需要做什么,并交流结果. 分别求出这两个四边形的对应边的长度,并分别量出这两个四边形各个内角的度数. 结论:均是相似多边形. 【例题】 例1 如图4所示,五边形ABCDE∽五边形A1B1C1D1E1,求C1D1的长和∠A的度数. 图4 【问题探索】 (1)相似多边形的性质是什么? (2)相似五边形中,对应边AB与A1B1,CD与C1D1之间有什么关系? (3)在比例式中,已知三条线段的长能否求出第四条线段的长?尝试求出C1D1的长. (4)根据相似多边形的性质,你能求出∠E的大小吗? (5)五边形的内角和是多少度? (6)由五边形内角和定理,能否求出∠A的值? 解:∵ 五边形ABCDE∽五边形A1B1C1D1E1, ∴ ,∠E=∠E1=145°. ∵ AB=15,A1B1=10,CD=21, ∴ ,解得C1D1=14. 又∵ ∠B=130°,∠C=∠D=90°, ∴ ∠A=(5-2)×180°-130°-145°-2×90°=85°. ∴ C1D1=14,∠A=85°. 把分析问题的过程设置成小问题的形式,通过教师的引导或者小组合作交流,学生层层递进的方式分析并解决问题,降低了学习难度,进一步培养学生分析问题的能力. 通过问题的形式教师逐步引导学生了解相似多边形的各个性质. 通过以上问题得出的结论,推导出图3中均是相似多边形. 通过例题,让学生掌握相似多边形的各个性质.
3.学以致用,应用新知 考点1 相似多边形的性质 练习1 如图,四边形ABCD~四边形A1B1C1D1,∠A=116°,∠B=40°,∠C=65°,求x的值和∠D1的度数.
解:∵∠A=116°,∠B=40°,∠C=65°, ∴∠D=360°-116°-40°-65°=139°. ∵四边形ABCD~四边形A1B1C1D1, ∴∠D1=∠D=139°,. ∴, ∴x=. 变式训练1 如图,平行四边形ABCD∽平行四边形AEFB,且AB=3 cm,BC=6 cm.求AE的长. 解:∵ 平行四边形ABCD∽平行四边形AEFB, ∴ . 又∵ AB=3 cm,BC=6 cm,EF=AB=3 cm, ∴ AE=(cm). 巩固相似多边形的性质,加深对所学知识的理解,提高学生知识的综合运用能力.
4.随堂训练,巩固新知 1.放大镜中的多边形与原多边形的关系是( ) A.形状不同,大小不同 B.形状相同,大小相同 C.形状相同,大小不同 D.形状不同,大小相同 答案:C 2.给出下列命题:①所有的正方形都相似;②所有的矩形都相似;③所有的三角形都相似;④所有的等腰直角三角形都相似;⑤所有的正五边形都相似.其中,正确命题为 ( ) A.①②③ B.①③⑤ C.①④⑤ D.②④⑤ 答案:C 3.在矩形ABCD中,AB=4,BC=3,下列四个矩形中与矩形ABCD相似的是( ) A B C D 4.若△ABC∽△A′B′C′,且AB︰A′B′=1∶2,则△ABC与△A′B′C′相似比是 ,△A′B′C′与△ABC的相似比是 . 答案: 2 5.如图所示,六边形ABCDEF与六边形A'B'C'D'E'F'相似,已知AB=5 cm,EF=6 cm,CD与C'D'的比为1∶3,∠E=125°,求A'B',E'F'的长及∠E'的度数. 解:∵ 六边形ABCDEF与六边形A'B'C'D'E'F'相似, ∴ ,∠E′=∠E=125°. ∴ A'B'=3AB=15 cm,E'F'=3EF=18 cm. 6.如图所示的两个矩形相似吗?为什么? 解:矩形ABCD ∽ 矩形EFGH, 因为它们的对应角相等,对应边的比也相等. 知识的综合运用,通过本环节的学习,让学生巩固所学知识.
5.课堂小结,自我完善 本节课所学知识: 1.相似图形的概念 2.相似多边形的定义 3.相似多边形的性质 4.相似比的定义 通过学生自我反思、小组交流、引导学生自主完成对本节重要知识技能和思想方法的小结.
6.布置作业 课本P95习题A组,B组 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 25.7 相似多边形和图形的位似 第1课时 相似多边形 1.相似图形: (1)概念:我们把形状相同的图形叫做相似图形. 2.相似多边形 (1)定义:一般地,如果两个多边形的对应角相等、对应边成比例,那么这两个多边形叫做相似多边形. (2)性质:对应角相等;对应边成比例. 3.相似比 (1)定义:相似多边形对应边的比叫做相似比. 提纲掣领,重点突出.
教后反思 本节课主要是相似多边形的定义,这节课主要是让学生自学,将定义和相似比等概念进行理解记忆,通过与相似三角形的定义的对比,得到相似多边形的相关概念. 反思,更进一步提升.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
