27.2反比例函数的图像和性质(第2课时 反比例函数的性质)教学设计(表格式)冀教版数学九年级上册
文档属性
| 名称 | 27.2反比例函数的图像和性质(第2课时 反比例函数的性质)教学设计(表格式)冀教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-20 00:00:00 | ||
图片预览



文档简介
27.2 反比例函数的图像和性质
课题 第2课时 反比例函数的性质 授课类型 新授课
授课人
教学内容 课本P134-137
教学目标 1.通过反比例函数的表达式及图像的确立,经历探索反比例函数性质的过程,理解并掌握反比例函数的性质. 2.通过探索反比例函数性质的过程,培养观察、分析、归纳和概括的能力,提高从图像中获取信息的能力.
教学重难点 重点:归纳、概括出图像位置及y随x的变化规律与比例系数k的关系. 难点:对反比例函数性质全面、深入地理解以及应用性质解决实际问题.
教学准备 多媒体课件
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 正比例函数与反比例函数的对比 函 数正比例函数反比例函数图 像 及名称 直线 双曲线解析式y=kx(k≠0)y=k/x(k≠0)图像的 位置k>0时,在一、三象限k<0时,在二、四象限性 质k>0时,y随x增大而增大k<0时,y随x增大而减小
反比例函数的图像在哪些象限,其增减性是怎样的? 本节就让我们一起来学习吧! 通过对正比例函数图像及其性质的复习,为引入反比例函数的图像及性质作铺垫,做到自然过渡,完成由正比例函数到反比例函数的知识迁移,从而引出课题.
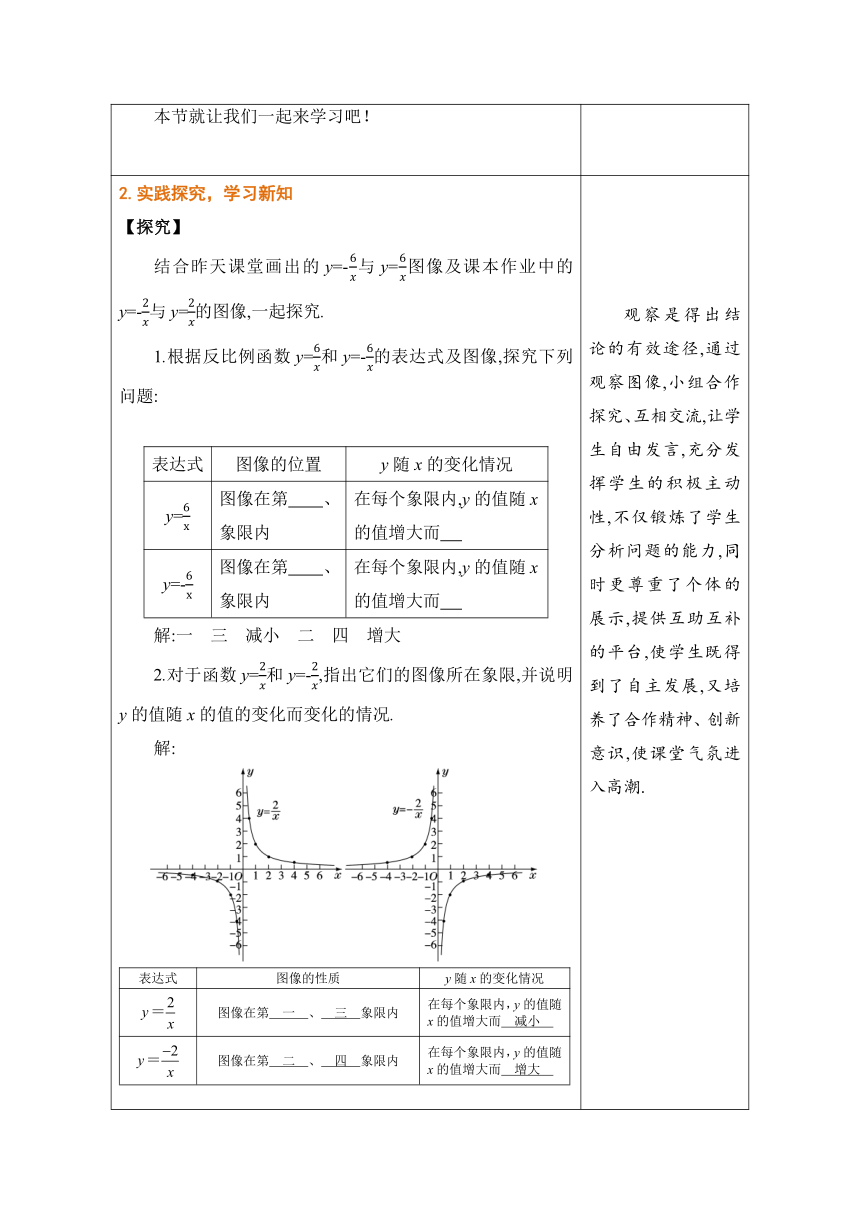
2.实践探究,学习新知 【探究】 结合昨天课堂画出的y=-与y=图像及课本作业中的y=-与y=的图像,一起探究. 1.根据反比例函数y=和y=-的表达式及图像,探究下列问题: 表达式图像的位置y随x的变化情况y=图像在第 、 象限内 在每个象限内,y的值随x的值增大而 y=-图像在第 、 象限内 在每个象限内,y的值随x的值增大而
解:一 三 减小 二 四 增大 2.对于函数y=和y=-,指出它们的图像所在象限,并说明y的值随x的值的变化而变化的情况. 解: 表达式图像的性质y随x的变化情况图像在第 一 、 三 象限内在每个象限内,y的值随x的值增大而 减小 图像在第 二 、 四 象限内在每个象限内,y的值随x的值增大而 增大
即: y=图像的两个分支分别位于第一、三象限内;在每个象限内y随x的增大而减小;y=-图像的两个分支分别位于第二、四象限内;在每个象限内y随x的增大而增大. 教师活动:提出以下问题. (1)反比例函数图像的形状是什么 (2)反比例函数图像无限延伸后与x轴、y轴有公共点吗 反比例函数图像关于原点O对称吗 (3)函数图像在哪个象限内 函数表达式中谁决定函数图像的位置 (4)观察函数图像,在每个象限内随着x的增大, y如何变化 函数表达式中谁决定函数图像的增减性 学生活动:独立思考后,小组进行交流. (1)双曲线. (2)反比例函数图像无限延伸后与x轴、 y轴没有交点,关于原点O 对称. (3)当k>0时,双曲线的两支分别位于第一、三象限; 当k<0时,双曲线的两支分别位于第二、四象限. 函数表达式中k的取值决定函数图像的位置 (4)当k>0时,在每个象限内,y随x的增大而减小; 当k<0时,在每个象限内,y随x的增大而增大.函数表达式中k的取值决定函数图像的增减性. 【归纳总结】 对于反比例函数y=,图像是双曲线,它具有以下性质: 1.当k>0时,它的图像位于第一、三象限,在每个象限内,y的值随x的值增大而减小; 当k<0时,它的图像位于第二、四象限,在每个象限内,y的值随x的值增大而增大. 3.双曲线的两支向两边无限延伸,与坐标轴没有交点; 4.双曲线的两支关于坐标原点成中心对称. 【例题】 例1 反比例函数的图像如图所示. (1)判断k为正数还是负数. (2)如果A(-3,y1)和B(-1,y2)为这个函数图像上的两点,那么y1与y2的大小关系是怎样的 解:(1)∵反比例函数的图像在第一、三象限, ∴ k>0. 由k>0可知,在每个象限内, y的值随x的值增大而减小. ∵ -3<-1,∴ y1>y2. 观察是得出结论的有效途径,通过观察图像,小组合作探究、互相交流,让学生自由发言,充分发挥学生的积极主动性,不仅锻炼了学生分析问题的能力,同时更尊重了个体的展示,提供互助互补的平台,使学生既得到了自主发展,又培养了合作精神、创新意识,使课堂气氛进入高潮. 通过例题的训练,让学生巩固用计算器计算任意锐角的三角函数值的按键步骤及方法.,并增强学生对所学知识的应用意识. 根据上面的函数图像归纳总结出反比例函数图像的性质. 本例题主要针对本节课的内容,重点考查学生对于k的正负性与图像所在象限以及y的值随x的值变化而变化的关系的认识,增强学生数形结合的思想意识.
3.学以致用,应用新知 考点1 反比例函数值的变化情况与k的关系 练习1 若函数y=nx|n|-2是反比例函数,且x>0时,y随x的增大而减小,则n的值是( ) A.±1 B.1 C.-1 D.不能确定 答案:B 解析:∵y=nx|n|-2是反比例函数, ∴|n|-2=-1, 解得n=±1. ∵当x>0时,y随着x的增大而减小, ∴反比例函数的图像一支位于第一象限, 则n>0, ∴n=1. 变式训练1 已知反比例函数y=,在它图像的每个分支上,y都随x的增大而增大,则k的值可以是( ) A.0 B.3 C.6 D.9 答案:A 考点2 比例系数k的几何意义 练习2 如图所示,点A在反比例函数(x >0)的图像上,AB⊥x轴于点B,AC⊥y轴于点C,你能求出矩形OBAC的面积吗 解:设点A的坐标为(x,y),则xy=3. 所以 S矩形OBAC= xy=3. 【归纳总结】 在反比例函数(k>0)的图像上任取一点P,过点P分别作x轴、y轴的垂线,与坐标轴围成的矩形面积为S,则S=. 结论 反比例函数(k≠0)中比例系数k的几何意义: . 变式训练2 如图,矩形AOBC的面积为4,反比例函数的图像的一支经过矩形对角线的交点P,则该反比例函数的表达式是( ) A. B. C. D. 解析:过点P作PD⊥OB(图略),由矩形的性质可知S△OPD=S矩形AOBC=,由反比例函数的几何意义可知S△OPD==,解得k=±1.又因为反比例函数图象在第一象限,所以k>0,所以k=1,所以.故选C. 答案:C 比例系数k的几何意义解题步骤: 运用k的几何意义解决问题,一般要通过双曲线上的点向x轴或y轴作垂线,构造矩形,矩形面积等于,或连接双曲线上的点和原点,再通过双曲线上的点向x轴或y轴作垂线,构造直角三角形,三角形面积等于,利用面积最终得到函数表达式. 巩固学生对反比例函数的图象和性质的认识和理解,并整理、总结对应的解题方法.
4.随堂训练,巩固新知 1.已知反比例函数,下列结论不正确的是( ) A.图像经过点(1,1) B.图像在第一、三象限 C.当x<0时,y<0 D.当x<0时,y随着x的增大而增大 答案:D 如图,A是反比例函数的图像上的一点,AB⊥x轴于点B,且△ABO的面积是3,则k的值是( ) A.3 B.-3 C.6 D.-6 答案:C 3.函数y1=x(x≥0),(x>0)的图像如图11所示,下列结论:(1)两函数图像的交点坐标为A(2,2);(2)当x>2时,y2>y1;(3)直线x=1分别与两函数图像交于B,C两点,则线段BC的长为3;(4)当x逐渐增大时,y1的值随着x的增大而增大,y2的值随着x的增大而减小.则其中正确的是( ) A.只有(1)(2) B.只有(1)(3) C.只有(2)(4) D.只有(1)(3) 答案:D 4.已知反比例函数的图像经过点A(2,6). (1)求此反比例函数的表达式. (2)这个函数的图像位于第几象限?y随x的增大如何变化? (3)点B(3,4),C,D(2,5)是否在这个函数的图像上? 解:(1)设. 因为点A(2,6)在函数图象上,所以, 解得k=12,因此. (2)因为k>0,所以函数图像位于第一、三象限,在每个象限内,y随x的增大而减小. (3)将B,C,D三点的坐标分别代入,得B,C两点的坐标满足表达式,D点坐标不满足表达式,所以B,C两点在函数图像上,D点不在函数图像上. 知识的综合运用,通过本环节的学习,让学生巩固所学知识.
5.课堂小结,自我完善 1.反比例函数的性质 一般地,反比例函数(k≠0)的图像是双曲线,它具有以下性质: 1.当k>0时,它的图像位于第一、三象限,在每个象限内,y的值随x的值增大而减小; 2.当k<0时,它的图像位于第二、四象限,在每个象限内,y的值随x的值增大而增大; 3.双曲线的两支向两边无限延伸,与坐标轴没有交点; 4.双曲线的两支关于坐标原点成中心对称. 2.反比例函数(k≠0)中比例系数k的几何意义: . 通过学生自我反思、小组交流、引导学生自主完成对本节重要知识技能和思想方法的小结.
6.布置作业 课本P113习题A组,B组 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 27.2 反比例函数的图像和性质 第2课时 反比例函数的性质 反比例函数的性质 当k>0时,它的图像位于第一、三象限,在每个象限内,y的值随x的值增大而减小; 当k<0时,它的图像位于第二、四象限,在每个象限内,y的值随x的值增大而增大. 反比例函数(k≠0)中比例系数k的几何意义: . 提纲掣领,重点突出.
教后反思 本节是学习用计算器求三角函数值并加以实际应用的内容,通过本节的学习,可以使学生充分认识到三角函数知识在现实世界中有着广泛的应用. 反思,更进一步提升.
课题 第2课时 反比例函数的性质 授课类型 新授课
授课人
教学内容 课本P134-137
教学目标 1.通过反比例函数的表达式及图像的确立,经历探索反比例函数性质的过程,理解并掌握反比例函数的性质. 2.通过探索反比例函数性质的过程,培养观察、分析、归纳和概括的能力,提高从图像中获取信息的能力.
教学重难点 重点:归纳、概括出图像位置及y随x的变化规律与比例系数k的关系. 难点:对反比例函数性质全面、深入地理解以及应用性质解决实际问题.
教学准备 多媒体课件
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 正比例函数与反比例函数的对比 函 数正比例函数反比例函数图 像 及名称 直线 双曲线解析式y=kx(k≠0)y=k/x(k≠0)图像的 位置k>0时,在一、三象限k<0时,在二、四象限性 质k>0时,y随x增大而增大k<0时,y随x增大而减小
反比例函数的图像在哪些象限,其增减性是怎样的? 本节就让我们一起来学习吧! 通过对正比例函数图像及其性质的复习,为引入反比例函数的图像及性质作铺垫,做到自然过渡,完成由正比例函数到反比例函数的知识迁移,从而引出课题.
2.实践探究,学习新知 【探究】 结合昨天课堂画出的y=-与y=图像及课本作业中的y=-与y=的图像,一起探究. 1.根据反比例函数y=和y=-的表达式及图像,探究下列问题: 表达式图像的位置y随x的变化情况y=图像在第 、 象限内 在每个象限内,y的值随x的值增大而 y=-图像在第 、 象限内 在每个象限内,y的值随x的值增大而
解:一 三 减小 二 四 增大 2.对于函数y=和y=-,指出它们的图像所在象限,并说明y的值随x的值的变化而变化的情况. 解: 表达式图像的性质y随x的变化情况图像在第 一 、 三 象限内在每个象限内,y的值随x的值增大而 减小 图像在第 二 、 四 象限内在每个象限内,y的值随x的值增大而 增大
即: y=图像的两个分支分别位于第一、三象限内;在每个象限内y随x的增大而减小;y=-图像的两个分支分别位于第二、四象限内;在每个象限内y随x的增大而增大. 教师活动:提出以下问题. (1)反比例函数图像的形状是什么 (2)反比例函数图像无限延伸后与x轴、y轴有公共点吗 反比例函数图像关于原点O对称吗 (3)函数图像在哪个象限内 函数表达式中谁决定函数图像的位置 (4)观察函数图像,在每个象限内随着x的增大, y如何变化 函数表达式中谁决定函数图像的增减性 学生活动:独立思考后,小组进行交流. (1)双曲线. (2)反比例函数图像无限延伸后与x轴、 y轴没有交点,关于原点O 对称. (3)当k>0时,双曲线的两支分别位于第一、三象限; 当k<0时,双曲线的两支分别位于第二、四象限. 函数表达式中k的取值决定函数图像的位置 (4)当k>0时,在每个象限内,y随x的增大而减小; 当k<0时,在每个象限内,y随x的增大而增大.函数表达式中k的取值决定函数图像的增减性. 【归纳总结】 对于反比例函数y=,图像是双曲线,它具有以下性质: 1.当k>0时,它的图像位于第一、三象限,在每个象限内,y的值随x的值增大而减小; 当k<0时,它的图像位于第二、四象限,在每个象限内,y的值随x的值增大而增大. 3.双曲线的两支向两边无限延伸,与坐标轴没有交点; 4.双曲线的两支关于坐标原点成中心对称. 【例题】 例1 反比例函数的图像如图所示. (1)判断k为正数还是负数. (2)如果A(-3,y1)和B(-1,y2)为这个函数图像上的两点,那么y1与y2的大小关系是怎样的 解:(1)∵反比例函数的图像在第一、三象限, ∴ k>0. 由k>0可知,在每个象限内, y的值随x的值增大而减小. ∵ -3<-1,∴ y1>y2. 观察是得出结论的有效途径,通过观察图像,小组合作探究、互相交流,让学生自由发言,充分发挥学生的积极主动性,不仅锻炼了学生分析问题的能力,同时更尊重了个体的展示,提供互助互补的平台,使学生既得到了自主发展,又培养了合作精神、创新意识,使课堂气氛进入高潮. 通过例题的训练,让学生巩固用计算器计算任意锐角的三角函数值的按键步骤及方法.,并增强学生对所学知识的应用意识. 根据上面的函数图像归纳总结出反比例函数图像的性质. 本例题主要针对本节课的内容,重点考查学生对于k的正负性与图像所在象限以及y的值随x的值变化而变化的关系的认识,增强学生数形结合的思想意识.
3.学以致用,应用新知 考点1 反比例函数值的变化情况与k的关系 练习1 若函数y=nx|n|-2是反比例函数,且x>0时,y随x的增大而减小,则n的值是( ) A.±1 B.1 C.-1 D.不能确定 答案:B 解析:∵y=nx|n|-2是反比例函数, ∴|n|-2=-1, 解得n=±1. ∵当x>0时,y随着x的增大而减小, ∴反比例函数的图像一支位于第一象限, 则n>0, ∴n=1. 变式训练1 已知反比例函数y=,在它图像的每个分支上,y都随x的增大而增大,则k的值可以是( ) A.0 B.3 C.6 D.9 答案:A 考点2 比例系数k的几何意义 练习2 如图所示,点A在反比例函数(x >0)的图像上,AB⊥x轴于点B,AC⊥y轴于点C,你能求出矩形OBAC的面积吗 解:设点A的坐标为(x,y),则xy=3. 所以 S矩形OBAC= xy=3. 【归纳总结】 在反比例函数(k>0)的图像上任取一点P,过点P分别作x轴、y轴的垂线,与坐标轴围成的矩形面积为S,则S=. 结论 反比例函数(k≠0)中比例系数k的几何意义: . 变式训练2 如图,矩形AOBC的面积为4,反比例函数的图像的一支经过矩形对角线的交点P,则该反比例函数的表达式是( ) A. B. C. D. 解析:过点P作PD⊥OB(图略),由矩形的性质可知S△OPD=S矩形AOBC=,由反比例函数的几何意义可知S△OPD==,解得k=±1.又因为反比例函数图象在第一象限,所以k>0,所以k=1,所以.故选C. 答案:C 比例系数k的几何意义解题步骤: 运用k的几何意义解决问题,一般要通过双曲线上的点向x轴或y轴作垂线,构造矩形,矩形面积等于,或连接双曲线上的点和原点,再通过双曲线上的点向x轴或y轴作垂线,构造直角三角形,三角形面积等于,利用面积最终得到函数表达式. 巩固学生对反比例函数的图象和性质的认识和理解,并整理、总结对应的解题方法.
4.随堂训练,巩固新知 1.已知反比例函数,下列结论不正确的是( ) A.图像经过点(1,1) B.图像在第一、三象限 C.当x<0时,y<0 D.当x<0时,y随着x的增大而增大 答案:D 如图,A是反比例函数的图像上的一点,AB⊥x轴于点B,且△ABO的面积是3,则k的值是( ) A.3 B.-3 C.6 D.-6 答案:C 3.函数y1=x(x≥0),(x>0)的图像如图11所示,下列结论:(1)两函数图像的交点坐标为A(2,2);(2)当x>2时,y2>y1;(3)直线x=1分别与两函数图像交于B,C两点,则线段BC的长为3;(4)当x逐渐增大时,y1的值随着x的增大而增大,y2的值随着x的增大而减小.则其中正确的是( ) A.只有(1)(2) B.只有(1)(3) C.只有(2)(4) D.只有(1)(3) 答案:D 4.已知反比例函数的图像经过点A(2,6). (1)求此反比例函数的表达式. (2)这个函数的图像位于第几象限?y随x的增大如何变化? (3)点B(3,4),C,D(2,5)是否在这个函数的图像上? 解:(1)设. 因为点A(2,6)在函数图象上,所以, 解得k=12,因此. (2)因为k>0,所以函数图像位于第一、三象限,在每个象限内,y随x的增大而减小. (3)将B,C,D三点的坐标分别代入,得B,C两点的坐标满足表达式,D点坐标不满足表达式,所以B,C两点在函数图像上,D点不在函数图像上. 知识的综合运用,通过本环节的学习,让学生巩固所学知识.
5.课堂小结,自我完善 1.反比例函数的性质 一般地,反比例函数(k≠0)的图像是双曲线,它具有以下性质: 1.当k>0时,它的图像位于第一、三象限,在每个象限内,y的值随x的值增大而减小; 2.当k<0时,它的图像位于第二、四象限,在每个象限内,y的值随x的值增大而增大; 3.双曲线的两支向两边无限延伸,与坐标轴没有交点; 4.双曲线的两支关于坐标原点成中心对称. 2.反比例函数(k≠0)中比例系数k的几何意义: . 通过学生自我反思、小组交流、引导学生自主完成对本节重要知识技能和思想方法的小结.
6.布置作业 课本P113习题A组,B组 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 27.2 反比例函数的图像和性质 第2课时 反比例函数的性质 反比例函数的性质 当k>0时,它的图像位于第一、三象限,在每个象限内,y的值随x的值增大而减小; 当k<0时,它的图像位于第二、四象限,在每个象限内,y的值随x的值增大而增大. 反比例函数(k≠0)中比例系数k的几何意义: . 提纲掣领,重点突出.
教后反思 本节是学习用计算器求三角函数值并加以实际应用的内容,通过本节的学习,可以使学生充分认识到三角函数知识在现实世界中有着广泛的应用. 反思,更进一步提升.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
