28.3.3 圆内接四边形及其性质 教学设计(表格式)冀教版数学九年级上册
文档属性
| 名称 | 28.3.3 圆内接四边形及其性质 教学设计(表格式)冀教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-20 00:00:00 | ||
图片预览


文档简介
28.3.3 圆内接四边形及其性质
课题 圆内接四边形及其性质 授课类型 新授课
授课人
教学内容 课本P159-162
教学目标 1.理解圆内接四边形和四边形的外接圆的概念. 2.掌握圆内接四边形的性质,并会用此性质进行有关的计算和证明.
教学重难点 重点:同弧所对的圆周角相等、圆内接多边形的概念及圆内接四边形的性质. 难点:同弧所对的圆周角相等、圆内接四边形性质的探究过程及应用.
教学准备 多媒体课件
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 【复习回顾】 1.什么是圆心角、圆周角 2.同弧所对的圆周角和圆心角有什么关系 3.直径所对的圆周角是多少度 90°的圆周角所对的弦是直径吗 通过复习圆周角定理及推论,巩固与圆周角有关的知识,做好新旧知识之间的衔接,为本节课新知识的学习做铺垫.
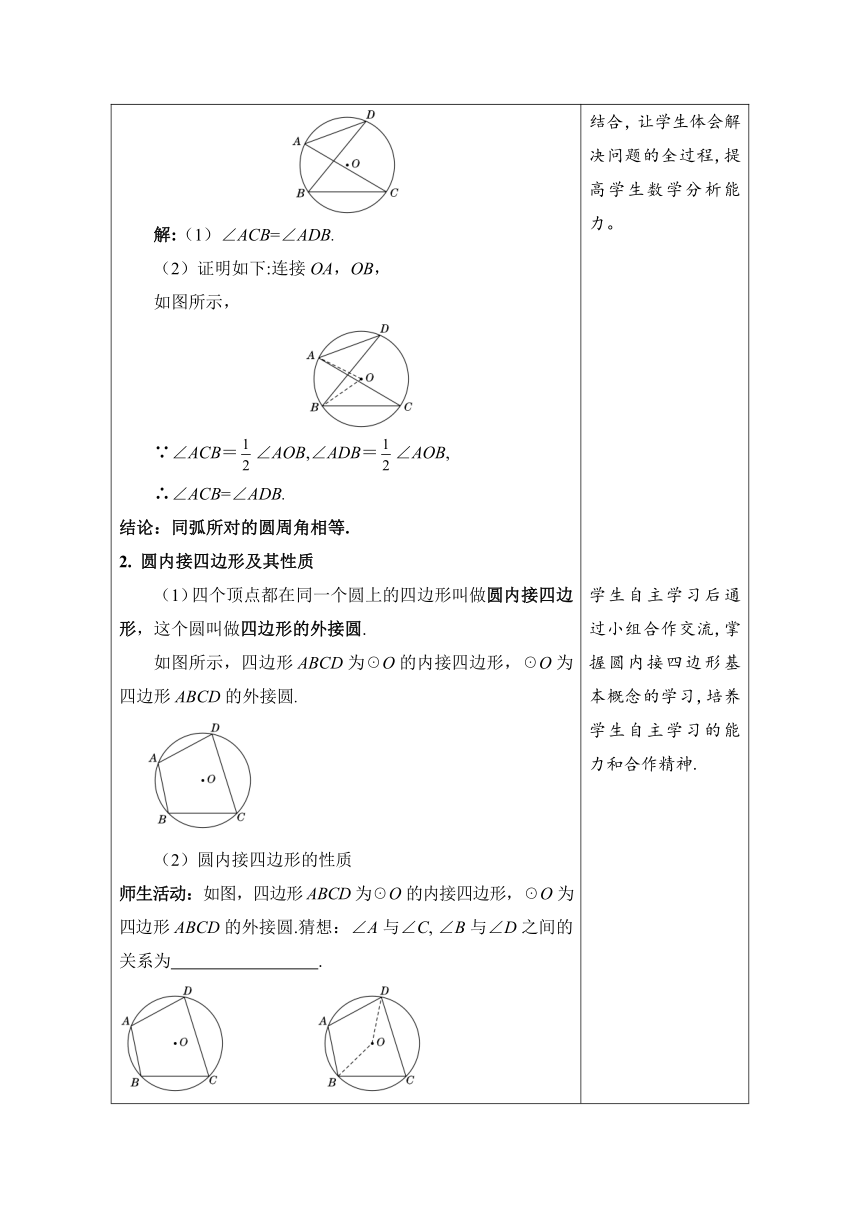
2.实践探究,学习新知 【探究】 1.同弧所对的圆周角 如图所示,∠ACB与∠ADB分别为☉O上同一条弧AB所对的两个圆周角. (1)∠ACB与∠ADB之间具有怎样的大小关系 (2)试证明你的猜想. 解:(1)∠ACB=∠ADB. (2)证明如下:连接OA,OB, 如图所示, ∵∠ACB=∠AOB,∠ADB=∠AOB, ∴∠ACB=∠ADB. 结论:同弧所对的圆周角相等. 2. 圆内接四边形及其性质 (1)四个顶点都在同一个圆上的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆. 如图所示,四边形ABCD为☉O的内接四边形,☉O为四边形ABCD的外接圆. (2)圆内接四边形的性质 师生活动:如图,四边形ABCD为☉O的内接四边形,☉O为四边形ABCD的外接圆.猜想:∠A与∠C, ∠B与∠D之间的关系为 . 师生活动:学生先独立思考,再小组内讨论、合作学习,然后教师组织学生交流,进行汇报. 【证明】连接OB,OD. ∵∠A所对的弧为,∠C所对的弧为, 又和所对的圆心角的和是周角, ∴∠A+∠C=360°÷2=180°. 同理∠B+∠D=180°. 结论:圆内接四边形的对角互补. 【例题】 例3 已知:如图28-3- 16,四边形ABCD为☉O的内接四边形,∠DCE为四边形ABCD的一个外角. 求证:∠DCE=∠BAD. 证明:∵四边形 ABCD为☉O的内接四边形, ∴∠BAD+∠BCD=180°. ∵∠BCD+∠DCE=180°, ∴∠DCE=∠BAD. 【知识拓展】 1.圆周角定理包含两个独立的条件,可以分开使用,即“同弧或等弧所对的圆周角相等”以及“在同圆或等圆中,同一条弧所对的圆周角等于这条弧所对的圆心角的一半”。 2.若将“同弧或等弧”改为“同弦或等弦”,则结论不一定成立. 3.圆内接四边形的外角等于它的内对角. 4.圆内接四边形性质是解决有关角的计算和证明常用的结论. 通过观察、思考、猜想、证明得到圆周角定理的推论,把直观猜想和理性思考相结合,让学生体会解决问题的全过程,提高学生数学分析能力。 学生自主学习后通过小组合作交流,掌握圆内接四边形基本概念的学习,培养学生自主学习的能力和合作精神. 在教师的引导下,通过层层深入分析已知条件,由圆周角和圆心角之间的关系,探究出圆内接四边形性质,提高学生分析问题、解决问题的能力,同时培养学生将语言叙述转化为几何语言的能力,以及严谨的学习态度. 通过完成例题的证明,体会圆内接四边形的性质的应用,培养学生的应用意识,同时证明了“圆内接四边形的外角等于它的内对角”这一性质.
3.学以致用,应用新知 考点1 圆内接四边形的对角互补 练习1 如图,AB为半圆O的直径,∠BAC=40°,D为弧AC上任意一点.求∠D的度数. 解:∵AB为半圆O的直径, ∴∠ACB=90°. ∵∠BAC=40°, ∴∠ABC=50°. 又∵四边形ABCD是圆内接四边形, ∴∠D+∠ABC=180°, ∴∠D=130°. 考点2 同弧所对的圆周角相等 练习2 如图,点A,B,C,D都在☉O上. (1)找出四对分别相等的圆周角. (2)如果∠DAC=∠BAC=60°,证明△BCD为等边三角形. 解:(1)∵同弧所对的圆周角相等, ∴∠ADB=∠ACB,∠BAC=∠BDC,∠DBC=∠DAC, ∠DCA=DBA. (2)∵∠DAC=∠BAC=60°, ∴∠DBC=∠BDC=60°, ∴∠BCD=60°, ∴△BCD是等边三角形. 巩固同弧所对的圆周角相等、圆内接四边形的性质的方法,加深对所学知识的理解,提高学生知识的综合运用能力.
4.随堂训练,巩固新知 1.如图,四边形ABCD是⊙O的内接四边形,BC是直径,∠C=75°,则∠A的度数为( ) A.90° B.75° C.140° D.105° 答案:D 2.如图,四边形ABCD内接于⊙O,若∠BOD=130°,则∠A的度数为( ) A.100° B.115° C.125° D.130° 答案:B 3.如图,四边形ABCD内接于⊙O,如果∠BOD的度数为122°,则∠DCE的度数为( ) A.64° B.61° C.62° D.60° 答案:B 4.如图,四边形ABCD为⊙O的内接四边形,AO⊥BC,垂足为点E,若∠ADC=130°,则∠BDC的度数为( ) A.70° B.80° C.75° D.60° 答案:B 5.如图,四边形ABCD是⊙O的内接四边形,延长BC到点E,则∠A与∠DCE的数量关系一定成立的是( ) A.∠A=∠DCE B.∠A+∠DCE=180° C.∠A+∠DCE=90° D.∠A>∠DCE 答案:A 6.如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠E=40°,∠ADC=85°,那么∠A的度数为 . 答案:45° 7.如图,四边形ABCD内接于半圆O(点A,B,C,D在半圆O上),AB为⊙O的直径,且∠ADC=110°,则∠BAC的度数为 度. 答案:20 知识的综合运用,通过本环节的学习,让学生巩固所学知识.
5.课堂小结,自我完善 1.同弧所对的圆周角相等. 2.圆内接四边形的有关概念. 3.圆内接四边形的性质:圆内接四边形的对角互补. 通过学生自我反思、小组交流、引导学生自主完成对本节重要知识技能和思想方法的小结.
6.布置作业 课本P161--162习题A组,B组 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 28.3.3 圆内接四边形 1.同弧所对的圆周角相等. 2.四个顶点都在同一个圆上的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆. 3. 圆内接四边形的性质:(1)圆内接四边形的对角互补;(2)圆内接四边形的外角等于它的内对角. 提纲掣领,重点突出.
教后反思 本节课探究同弧所对的圆周角相等和圆内接四边形的性质,都与圆周角的定理有关,所以导入新课时设计复习上节课的内容,为本节课做好铺垫,同时设计生活实际问题,激发学生的学习兴趣.本节课内容较为简单,在教学设计时,多设计学生参与活动的环节,让学生经历动手操作(度量)、猜想、验证、得出结论的探索过程,真正成为课堂的主人,在课堂上让学生通过自主学习、合作交流、质疑提升等教学活动学到人人有价值的数学. 反思,更进一步提升.
课题 圆内接四边形及其性质 授课类型 新授课
授课人
教学内容 课本P159-162
教学目标 1.理解圆内接四边形和四边形的外接圆的概念. 2.掌握圆内接四边形的性质,并会用此性质进行有关的计算和证明.
教学重难点 重点:同弧所对的圆周角相等、圆内接多边形的概念及圆内接四边形的性质. 难点:同弧所对的圆周角相等、圆内接四边形性质的探究过程及应用.
教学准备 多媒体课件
教与学互动设计(教学过程) 设计意图
1.创设情景,导入新课 【复习回顾】 1.什么是圆心角、圆周角 2.同弧所对的圆周角和圆心角有什么关系 3.直径所对的圆周角是多少度 90°的圆周角所对的弦是直径吗 通过复习圆周角定理及推论,巩固与圆周角有关的知识,做好新旧知识之间的衔接,为本节课新知识的学习做铺垫.
2.实践探究,学习新知 【探究】 1.同弧所对的圆周角 如图所示,∠ACB与∠ADB分别为☉O上同一条弧AB所对的两个圆周角. (1)∠ACB与∠ADB之间具有怎样的大小关系 (2)试证明你的猜想. 解:(1)∠ACB=∠ADB. (2)证明如下:连接OA,OB, 如图所示, ∵∠ACB=∠AOB,∠ADB=∠AOB, ∴∠ACB=∠ADB. 结论:同弧所对的圆周角相等. 2. 圆内接四边形及其性质 (1)四个顶点都在同一个圆上的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆. 如图所示,四边形ABCD为☉O的内接四边形,☉O为四边形ABCD的外接圆. (2)圆内接四边形的性质 师生活动:如图,四边形ABCD为☉O的内接四边形,☉O为四边形ABCD的外接圆.猜想:∠A与∠C, ∠B与∠D之间的关系为 . 师生活动:学生先独立思考,再小组内讨论、合作学习,然后教师组织学生交流,进行汇报. 【证明】连接OB,OD. ∵∠A所对的弧为,∠C所对的弧为, 又和所对的圆心角的和是周角, ∴∠A+∠C=360°÷2=180°. 同理∠B+∠D=180°. 结论:圆内接四边形的对角互补. 【例题】 例3 已知:如图28-3- 16,四边形ABCD为☉O的内接四边形,∠DCE为四边形ABCD的一个外角. 求证:∠DCE=∠BAD. 证明:∵四边形 ABCD为☉O的内接四边形, ∴∠BAD+∠BCD=180°. ∵∠BCD+∠DCE=180°, ∴∠DCE=∠BAD. 【知识拓展】 1.圆周角定理包含两个独立的条件,可以分开使用,即“同弧或等弧所对的圆周角相等”以及“在同圆或等圆中,同一条弧所对的圆周角等于这条弧所对的圆心角的一半”。 2.若将“同弧或等弧”改为“同弦或等弦”,则结论不一定成立. 3.圆内接四边形的外角等于它的内对角. 4.圆内接四边形性质是解决有关角的计算和证明常用的结论. 通过观察、思考、猜想、证明得到圆周角定理的推论,把直观猜想和理性思考相结合,让学生体会解决问题的全过程,提高学生数学分析能力。 学生自主学习后通过小组合作交流,掌握圆内接四边形基本概念的学习,培养学生自主学习的能力和合作精神. 在教师的引导下,通过层层深入分析已知条件,由圆周角和圆心角之间的关系,探究出圆内接四边形性质,提高学生分析问题、解决问题的能力,同时培养学生将语言叙述转化为几何语言的能力,以及严谨的学习态度. 通过完成例题的证明,体会圆内接四边形的性质的应用,培养学生的应用意识,同时证明了“圆内接四边形的外角等于它的内对角”这一性质.
3.学以致用,应用新知 考点1 圆内接四边形的对角互补 练习1 如图,AB为半圆O的直径,∠BAC=40°,D为弧AC上任意一点.求∠D的度数. 解:∵AB为半圆O的直径, ∴∠ACB=90°. ∵∠BAC=40°, ∴∠ABC=50°. 又∵四边形ABCD是圆内接四边形, ∴∠D+∠ABC=180°, ∴∠D=130°. 考点2 同弧所对的圆周角相等 练习2 如图,点A,B,C,D都在☉O上. (1)找出四对分别相等的圆周角. (2)如果∠DAC=∠BAC=60°,证明△BCD为等边三角形. 解:(1)∵同弧所对的圆周角相等, ∴∠ADB=∠ACB,∠BAC=∠BDC,∠DBC=∠DAC, ∠DCA=DBA. (2)∵∠DAC=∠BAC=60°, ∴∠DBC=∠BDC=60°, ∴∠BCD=60°, ∴△BCD是等边三角形. 巩固同弧所对的圆周角相等、圆内接四边形的性质的方法,加深对所学知识的理解,提高学生知识的综合运用能力.
4.随堂训练,巩固新知 1.如图,四边形ABCD是⊙O的内接四边形,BC是直径,∠C=75°,则∠A的度数为( ) A.90° B.75° C.140° D.105° 答案:D 2.如图,四边形ABCD内接于⊙O,若∠BOD=130°,则∠A的度数为( ) A.100° B.115° C.125° D.130° 答案:B 3.如图,四边形ABCD内接于⊙O,如果∠BOD的度数为122°,则∠DCE的度数为( ) A.64° B.61° C.62° D.60° 答案:B 4.如图,四边形ABCD为⊙O的内接四边形,AO⊥BC,垂足为点E,若∠ADC=130°,则∠BDC的度数为( ) A.70° B.80° C.75° D.60° 答案:B 5.如图,四边形ABCD是⊙O的内接四边形,延长BC到点E,则∠A与∠DCE的数量关系一定成立的是( ) A.∠A=∠DCE B.∠A+∠DCE=180° C.∠A+∠DCE=90° D.∠A>∠DCE 答案:A 6.如图,圆内接四边形ABCD两组对边的延长线分别相交于点E,F,且∠E=40°,∠ADC=85°,那么∠A的度数为 . 答案:45° 7.如图,四边形ABCD内接于半圆O(点A,B,C,D在半圆O上),AB为⊙O的直径,且∠ADC=110°,则∠BAC的度数为 度. 答案:20 知识的综合运用,通过本环节的学习,让学生巩固所学知识.
5.课堂小结,自我完善 1.同弧所对的圆周角相等. 2.圆内接四边形的有关概念. 3.圆内接四边形的性质:圆内接四边形的对角互补. 通过学生自我反思、小组交流、引导学生自主完成对本节重要知识技能和思想方法的小结.
6.布置作业 课本P161--162习题A组,B组 课后练习巩固,让所学知识得以运用,提高计算能力和做题效率.
板书设计 28.3.3 圆内接四边形 1.同弧所对的圆周角相等. 2.四个顶点都在同一个圆上的四边形叫做圆内接四边形,这个圆叫做四边形的外接圆. 3. 圆内接四边形的性质:(1)圆内接四边形的对角互补;(2)圆内接四边形的外角等于它的内对角. 提纲掣领,重点突出.
教后反思 本节课探究同弧所对的圆周角相等和圆内接四边形的性质,都与圆周角的定理有关,所以导入新课时设计复习上节课的内容,为本节课做好铺垫,同时设计生活实际问题,激发学生的学习兴趣.本节课内容较为简单,在教学设计时,多设计学生参与活动的环节,让学生经历动手操作(度量)、猜想、验证、得出结论的探索过程,真正成为课堂的主人,在课堂上让学生通过自主学习、合作交流、质疑提升等教学活动学到人人有价值的数学. 反思,更进一步提升.
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
