1.3.1空间直角坐标系 课件(共14张PPT)-高二上学期数学人教A版(2019)选择性必修第一册
文档属性
| 名称 | 1.3.1空间直角坐标系 课件(共14张PPT)-高二上学期数学人教A版(2019)选择性必修第一册 |  | |
| 格式 | pptx | ||
| 文件大小 | 13.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-19 21:17:55 | ||
图片预览




文档简介
(共14张PPT)
人教2019A版选择性必修 第一册
第一章 空间向量与立体几何
1.3 空间向量及其运算的坐标表示
1.3.1 空间直角坐标系
复习导入
共线向量定理:
共面向量定理:
单位正交基底:如果空间的一个基底的三个基向量互相垂直,且长都为1, 则这个基底叫做单位正交基底, 常用{ }表示.
空间向量的基本定理:
若是 空间的一个基底, 是空间任意一向量,存在唯一的实数组使
笛卡尔是谁?
他对世界有什么贡献?
新课导入
笛卡尔最为世人熟知的是其作为数学家的成就。他于1637年发明了现代数学的基础工具之一 —— 坐标系。
可以说,空间直角坐标系是笛卡尔二维坐标系在三维空间的自然延伸,其核心思想源于笛卡尔建立的“用代数方法研究几何”的框架,因此也常被归入“笛卡尔坐标系”的范畴。
今天,我们一起来学习空间向量的坐标表示......
空间直角坐标系与笛卡尔的思想有密切联系,但并非由他直接提出。
笛卡尔在17世纪创立了平面直角坐标系(二维笛卡尔坐标系),将几何问题代数化。后来,数学家们基于他的二维坐标系思想进行扩展,引入了三维空间的直角坐标系——通过三条两两垂直的数轴(x轴、y轴、z轴),将空间中的点与有序三元组(x,y,z)对应起来,从而实现空间几何与代数方程的结合。
新课导入
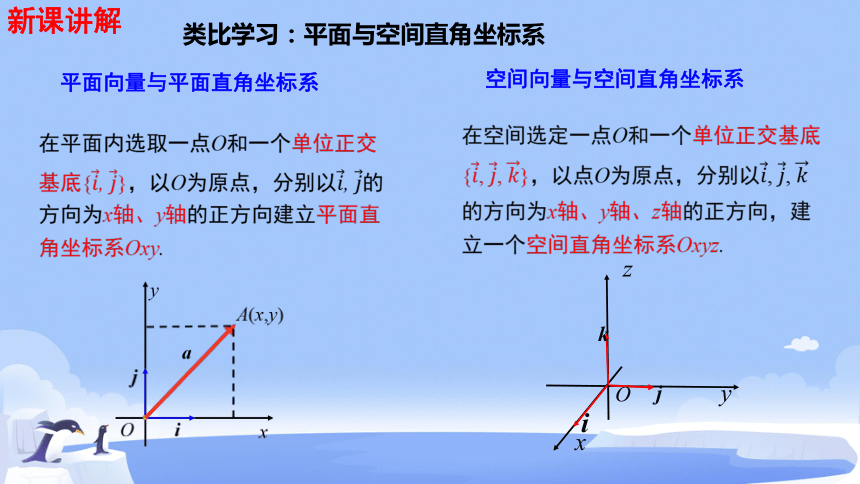
类比学面与空间直角坐标系
平面向量与平面直角坐标系
空间向量与空间直角坐标系
x
y
z
i
j
k
O
新课讲解
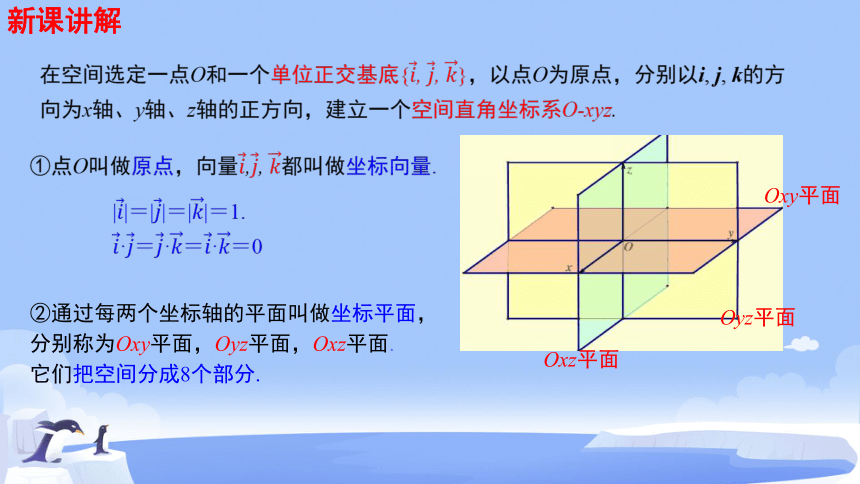
Oyz平面
Oxz平面
②通过每两个坐标轴的平面叫做坐标平面,
分别称为Oxy平面,Oyz平面,Oxz平面.
它们把空间分成8个部分.
Oxy平面
新课讲解
新课讲解
2
3
6
A(6,3,2)
新课讲解
点的位置 x轴上 y轴上 z轴上 xOy平面 xOz平面 yOz平面
点的坐标
(x, 0, 0)
(0, y, 0)
(0, 0, z)
(x, y, 0)
(x, 0, z)
(0, y, z)
已知点A(x , y , z) ,则:
①点A关于x轴对称的点为A1___________;
②点A关于y轴对称的点为A2___________;
③点A关于z轴对称的点为A3___________.
④点A关于原点对称的点为A4___________.
⑤点A关于Oxy平面对称的点为A5 __________;
⑥点A关于Oxz平面对称的点为A6 __________;
⑦点A关于Oyz平面对称的点为A7 __________.
(x , y , -z)
(-x , y , z)
(x , -y , z)
(x , -y , -z)
(-x , -y , z)
(-x , y , -z)
(-x , -y , -z)
规律:关于谁对称,谁就不变!其余互为相反数。
新课讲解
解析:(1)D'(0, 0, 2)
C(0, 4, 0)
A'(3, 0, 2)
B'(3, 4, 2)
例题解析
1.点A(-1,2,1)在x轴上的投影点和在xOy平面上的投影点的坐标分别为( )
A.(-1,0,1),(-1,2,0) B.(-1,0,0),(-1,2,0)
C.(-1,0,0),(-1,0,0) D.(-1,2,0),(-1,2,0)
2.点P(1,-2,5) 到xOy平面的距离为( )
A.1 B.2 C.-2 D.5
D
课堂练习
B
3.在空间直角坐标系Oxyz中,
(1)坐标平面____与x轴垂直,坐标平面_____与y轴垂直,坐标平面____与z轴垂直;
(2)写出点P(2,3,4)在三个坐标平面内的射影的坐标;
在Oyz平面内的射影坐标为________
在Oxz平面内的射影坐标为________
在Oxy平面内的射影坐标为________
(3)点P(1,3,5)关于原点成中心对称的点的坐标是________.
(4)点P(1,3,5)在x轴上的射影坐标为_________.
Oyz
Oxz
Oxy
(0,3,4)
(2,0,4)
(2,3,0)
(-1,-3,-5)
(1,0,0)
课堂练习
4.已知正四棱锥P ABCD的底面边长为 ,侧棱长为13,
建立的空间直角坐标系如图,写出各顶点的坐标.
课堂练习
回顾本节课的学习过程,我们是如何得到空间点和空间
向量的坐标表示的?
平面直角
坐标系
空间直角
坐标系
空间的点和空间向量的坐标表示
课堂小结
课后作业
人教2019A版选择性必修 第一册
第一章 空间向量与立体几何
1.3 空间向量及其运算的坐标表示
1.3.1 空间直角坐标系
复习导入
共线向量定理:
共面向量定理:
单位正交基底:如果空间的一个基底的三个基向量互相垂直,且长都为1, 则这个基底叫做单位正交基底, 常用{ }表示.
空间向量的基本定理:
若是 空间的一个基底, 是空间任意一向量,存在唯一的实数组使
笛卡尔是谁?
他对世界有什么贡献?
新课导入
笛卡尔最为世人熟知的是其作为数学家的成就。他于1637年发明了现代数学的基础工具之一 —— 坐标系。
可以说,空间直角坐标系是笛卡尔二维坐标系在三维空间的自然延伸,其核心思想源于笛卡尔建立的“用代数方法研究几何”的框架,因此也常被归入“笛卡尔坐标系”的范畴。
今天,我们一起来学习空间向量的坐标表示......
空间直角坐标系与笛卡尔的思想有密切联系,但并非由他直接提出。
笛卡尔在17世纪创立了平面直角坐标系(二维笛卡尔坐标系),将几何问题代数化。后来,数学家们基于他的二维坐标系思想进行扩展,引入了三维空间的直角坐标系——通过三条两两垂直的数轴(x轴、y轴、z轴),将空间中的点与有序三元组(x,y,z)对应起来,从而实现空间几何与代数方程的结合。
新课导入
类比学面与空间直角坐标系
平面向量与平面直角坐标系
空间向量与空间直角坐标系
x
y
z
i
j
k
O
新课讲解
Oyz平面
Oxz平面
②通过每两个坐标轴的平面叫做坐标平面,
分别称为Oxy平面,Oyz平面,Oxz平面.
它们把空间分成8个部分.
Oxy平面
新课讲解
新课讲解
2
3
6
A(6,3,2)
新课讲解
点的位置 x轴上 y轴上 z轴上 xOy平面 xOz平面 yOz平面
点的坐标
(x, 0, 0)
(0, y, 0)
(0, 0, z)
(x, y, 0)
(x, 0, z)
(0, y, z)
已知点A(x , y , z) ,则:
①点A关于x轴对称的点为A1___________;
②点A关于y轴对称的点为A2___________;
③点A关于z轴对称的点为A3___________.
④点A关于原点对称的点为A4___________.
⑤点A关于Oxy平面对称的点为A5 __________;
⑥点A关于Oxz平面对称的点为A6 __________;
⑦点A关于Oyz平面对称的点为A7 __________.
(x , y , -z)
(-x , y , z)
(x , -y , z)
(x , -y , -z)
(-x , -y , z)
(-x , y , -z)
(-x , -y , -z)
规律:关于谁对称,谁就不变!其余互为相反数。
新课讲解
解析:(1)D'(0, 0, 2)
C(0, 4, 0)
A'(3, 0, 2)
B'(3, 4, 2)
例题解析
1.点A(-1,2,1)在x轴上的投影点和在xOy平面上的投影点的坐标分别为( )
A.(-1,0,1),(-1,2,0) B.(-1,0,0),(-1,2,0)
C.(-1,0,0),(-1,0,0) D.(-1,2,0),(-1,2,0)
2.点P(1,-2,5) 到xOy平面的距离为( )
A.1 B.2 C.-2 D.5
D
课堂练习
B
3.在空间直角坐标系Oxyz中,
(1)坐标平面____与x轴垂直,坐标平面_____与y轴垂直,坐标平面____与z轴垂直;
(2)写出点P(2,3,4)在三个坐标平面内的射影的坐标;
在Oyz平面内的射影坐标为________
在Oxz平面内的射影坐标为________
在Oxy平面内的射影坐标为________
(3)点P(1,3,5)关于原点成中心对称的点的坐标是________.
(4)点P(1,3,5)在x轴上的射影坐标为_________.
Oyz
Oxz
Oxy
(0,3,4)
(2,0,4)
(2,3,0)
(-1,-3,-5)
(1,0,0)
课堂练习
4.已知正四棱锥P ABCD的底面边长为 ,侧棱长为13,
建立的空间直角坐标系如图,写出各顶点的坐标.
课堂练习
回顾本节课的学习过程,我们是如何得到空间点和空间
向量的坐标表示的?
平面直角
坐标系
空间直角
坐标系
空间的点和空间向量的坐标表示
课堂小结
课后作业
