1.1 探索勾股定理 教学设计 2025-2026学年数学北师大版八年级上册
文档属性
| 名称 | 1.1 探索勾股定理 教学设计 2025-2026学年数学北师大版八年级上册 |

|
|
| 格式 | DOCX | ||
| 文件大小 | 356.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-20 00:00:00 | ||
图片预览

文档简介
第一章 勾股定理
1 探索勾股定理
第1课时 认识勾股定理
1.用数格子的方法探索直角三角形的三边关系,掌握勾股定理的内容.
2.让学生经历“观察—猜想—归纳—验证”的数学思维过程,体会数形结合和从特殊到一般的思想方法.
3.探索并理解直角三角形三边之间的数量关系,提高学生的推理能力.
▲重点
探索勾股定理并利用勾股定理解决问题.
▲难点
在方格纸上通过计算图形面积的方法探索勾股定理.
活动1 创设情境 导入新课(课件)
如图,从电线杆离地面8 m处向地面拉一条钢索,钢索在地面的固定点距离电线杆底部6 m,你知道需要多长的钢索吗?
直角三角形三边长度存在一种特殊的关系,这节课我们一起探索勾股定理.
活动2 实践探究 交流新知
【探究1】
1.在纸上画若干个直角三角形,分别测量它们的三边长,看看三边长的平方之间有怎样的关系?与同伴进行交流.
2.(1)观察教材图1-2中左侧的图案,正方形A中有__9__个小方格,即A的面积为__9__平方单位.(投影教材图1-2)
正方形B中有__9__个小方格,即B的面积为__9__平方单位.
正方形C中有__18__个小方格,即C的面积为__18__平方单位.
(2)你是怎样得出上面的结果的?学生思考交流并加以回答.
(3)图1-2中,A,B,C的面积之间有什么关系?
学生交流后形成共识,教师板书:SA+SB=SC.
【探究2】
我们也不难发现教材图1-2中的直角三角形是等腰直角三角形.如果不是等腰直角三角形,而是一般的直角三角形,会不会也有这种关系呢?(投影教材图1-3)
(1)教材图1-3中,A,B,C的面积是否还满足上面的关系?你是如何计算的?
答:A,B,C的面积还满足上面的关系,即SA+SB=SC,是通过数格子的方法计算的.
(2)如果直角三角形的两直角边长分别为1.6个单位长度和2.4个单位长度,上面所猜想的数量关系还成立吗?
答:仍然成立.
(3)你能发现直角三角形三边长度之间的关系吗?
【归纳】勾股定理:直角三角形两直角边的平方和等于__斜边的平方__.如果用a,b和c分别表示直角三角形的两直角边和斜边,那么__a2+b2=c2__.
活动3 开放训练 应用举例
【例1】在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.
(1)若a=6,b=8,求c的值;
(2)若a=5,c=13,求b的值.
【方法指导】运用勾股定理求解.
解:(1)由勾股定理,得c2=a2+b2=62+82=100.
∵102=100,
∴c=10;
(2)由勾股定理,得b2=c2-a2=132-52=144.
∵122=144,
∴b=12.
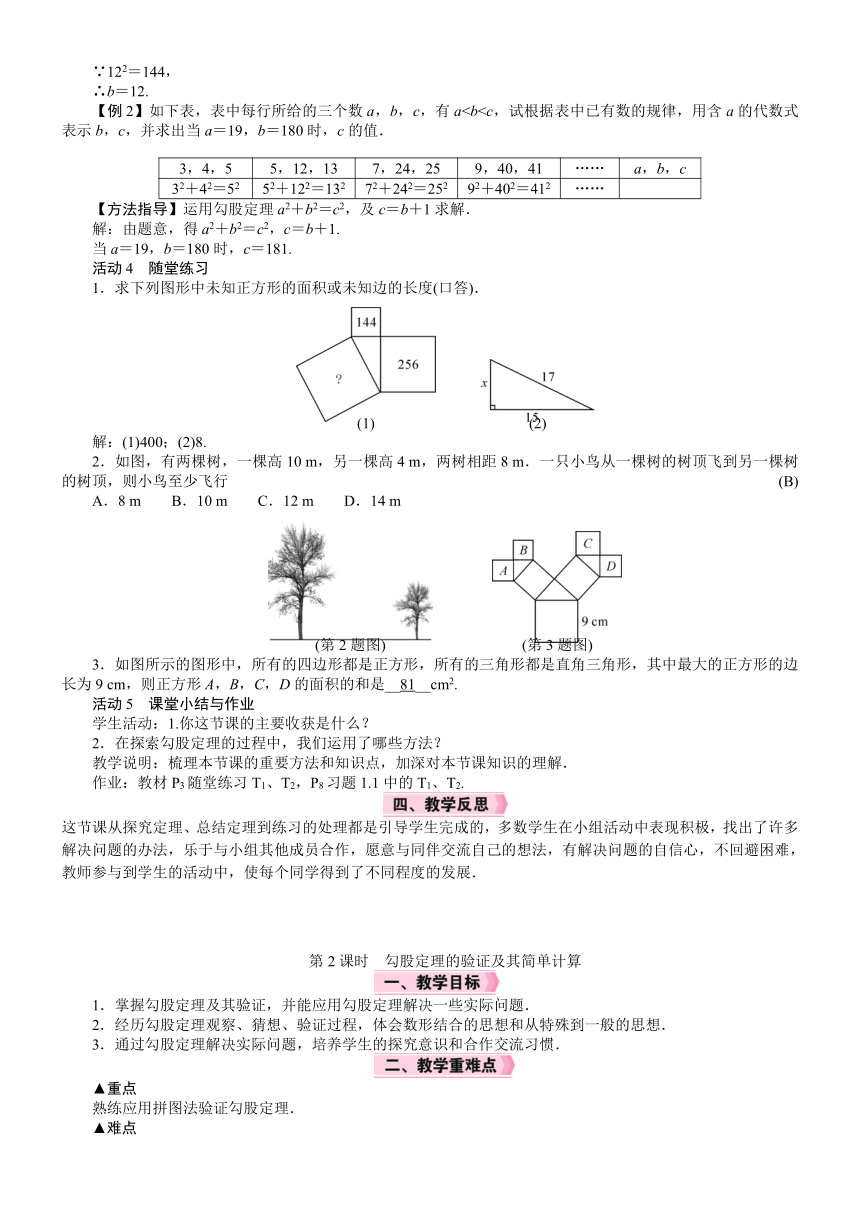
【例2】如下表,表中每行所给的三个数a,b,c,有a3,4,5 5,12,13 7,24,25 9,40,41 …… a,b,c
32+42=52 52+122=132 72+242=252 92+402=412 ……
【方法指导】运用勾股定理a2+b2=c2,及c=b+1求解.
解:由题意,得a2+b2=c2,c=b+1.
当a=19,b=180时,c=181.
活动4 随堂练习
1.求下列图形中未知正方形的面积或未知边的长度(口答).
解:(1)400;(2)8.
2.如图,有两棵树,一棵高10 m,另一棵高4 m,两树相距8 m.一只小鸟从一棵树的树顶飞到另一棵树的树顶,则小鸟至少飞行 (B)
A.8 m B.10 m C.12 m D.14 m
3.如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为9 cm,则正方形A,B,C,D的面积的和是__81__cm2.
活动5 课堂小结与作业
学生活动:1.你这节课的主要收获是什么?
2.在探索勾股定理的过程中,我们运用了哪些方法?
教学说明:梳理本节课的重要方法和知识点,加深对本节课知识的理解.
作业:教材P3随堂练习T1、T2,P8习题1.1中的T1、T2.
这节课从探究定理、总结定理到练习的处理都是引导学生完成的,多数学生在小组活动中表现积极,找出了许多解决问题的办法,乐于与小组其他成员合作,愿意与同伴交流自己的想法,有解决问题的自信心,不回避困难,教师参与到学生的活动中,使每个同学得到了不同程度的发展.
第2课时 勾股定理的验证及其简单计算
1.掌握勾股定理及其验证,并能应用勾股定理解决一些实际问题.
2.经历勾股定理观察、猜想、验证过程,体会数形结合的思想和从特殊到一般的思想.
3.通过勾股定理解决实际问题,培养学生的探究意识和合作交流习惯.
▲重点
熟练应用拼图法验证勾股定理.
▲难点
用勾股定理解决问题.
活动1 创设情境 导入新课(课件)
据说,古埃及人曾用如图所示的方法画直角.
这种方法对吗?今天我们就来一起判断一下吧!
活动2 实践探究 交流新知
【探究1】拼图验证勾股定理
如下课件中图①是四个全等的直角三角形,两直角边分别为a和b,斜边为c.请你开动脑筋,用它们拼出一个正方形,对勾股定理进行验证.
问题1:图②中正方形ABCD的边长是__a+b__,正方形ABCD的面积可表示为__(a+b)2__.
问题2:图②中正方形ABCD由四个全等的直角三角形和一个小正方形组成,因此正方形ABCD的面积还可以表示为__4×ab+c2__.
问题3:观察两种表示方法,它们表示的是同一个图形的面积,所以结果应__相等__.
问题4:现在,你能验证勾股定理吗?
问题5:利用图③如何验证勾股定理?
【探究2】深入了解勾股定理的证法
自主探究
阅读教材P4尝试·思考.
问题1:画一个直角三角形,分别以这个直角三角形的三边为边长向外作正方形,你能利用这个图证明勾股定理的正确性吗?你是如何做的?与同伴进行交流.
合作探究
问题2:为了计算教材P4图1-4中大正方形的面积,小明对这个大正方形适当割补后,分别得到教材P4图1-5、图1-6.
(1)将所有三角形和正方形的面积用a,b,c的式子表示出来.
(2)教材图1-5、图1-6中正方形ABCD的面积分别是多少?你有哪些表示方式?
(3)你能分别利用教材图1-5、图1-6验证勾股定理吗?
解:(3)图1-5:(a+b)2=×4+c2,化简,得:a2+b2=c2;
图1-6:×4+(b-a)2=c2,化简,得:a2+b2=c2.
问题3:你能利用教材P5图1-7,1-8验证勾股定理吗?
解:图1-7:52=×4+12,即52=32+42;
图1-8:设直角三角形中,较长直角边为b,较短直角边为a,斜边长为c,则c2=×4+(b-a)2,即c2=a2+b2.
问题4:如果一个三角形是钝角三角形或锐角三角形,它的三边长能满足“较长边的平方等于另外两边的平方和”吗?
解:观察教材P6图1-10,不能满足.
【归纳】勾股定理的证明方法有300多种,必须是直角三角形的三边才能满足a2+b2=c2.
同学们可以阅读教材P6-7其他证明勾股定理的方法.
活动3 开放训练 应用举例
【例1】(教材P5例题)在一次军事演习中,红方侦察员王叔叔在距离东西向公路400 m处侦察,发现一辆蓝方汽车在公路上疾驶.他用红外测距仪测得汽车与他相距400 m;过了10 s,测得汽车与他相距500 m.你能帮王叔叔计算蓝方汽车这10 s的平均速度吗?
【方法指导】
(1)根据题意画出简单的示意图如图所示.
(2)在直角三角形中已知什么边?要求什么边?
在直角三角形中已知斜边和一条直角边,要求另一条直角边.
(3)如何计算蓝方汽车的速度?
由题意,得AC=__400_m__,AB=__500_m__,由勾股定理,得BC=__300_m__,
所以蓝方汽车这10 s的平均速度为__300÷10=30(m/s)__.
【例2】(教材P6随堂练习)如图是某沿江地区交通平面图的一部分(单位:km),为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速公路,已知沿江高速公路的建设成本是5 000万元/km,该沿江高速公路的建设成本预计是多少?
【方法指导】利用勾股定理求出斜边OM,OQ的长,再计算建设成本.
解:在Rt△MON中,由勾股定理,得OM2=MN2+NO2,
即OM2=302+402=2 500,
∴OM=50 km.
在Rt△OPQ中,由勾股定理,得OQ2=OP2+PQ2,
即OQ2=502+1202=16 900,
∴OQ=130 km,
5 000×(50+130)=900 000(万元).
答:该沿江高速公路的建设成本预计是900 000万元.
活动4 随堂练习
1.放学以后,小红和小颖分别沿着东北方向和西北方向回家,若小红和小颖行走的速度都是40 m/min,小红用15 min到家,小颖用20 min到家,小红和小颖家的距离为 (C)
A.600 m B.800 m
C.1 000 m D.不能确定
2.如图,在四边形ABCD中,∠BAD=90°,∠CBD=90°,AD=4,AB=3,BC=12,则以DC为边的正方形DCEF的面积是__169__.
3.如图,一架云梯长10 m,斜靠在一面墙上,梯子顶端离地面6 m,要使梯子顶端离地面8 m,则梯子的底部在水平方向要向左滑动__2__m.
4.如图,受某次台风的影响,一棵高18 m的大树断裂,树的顶部落在离树根底部12 m处,这棵树断裂后有多高?
解:设这棵树断裂后高x m.
根据题意,得x2+122=(18-x)2,
解得x=5.
答:这棵树断裂后高5 m.
活动5 课堂小结与作业
学生活动:谈谈本节课的收获与体会.
教学说明:学生先独立完成小结,在学生回答的过程中,老师引导学生将本节课的知识系统化.
作业:教材P8~9习题1.1中的T4、T6、T7.
勾股定理的验证既是本节课的重点,也是本节课的难点,为了突破这一难点,设计了拼图活动,先让学生从形上感知,再层层设问,从面积入手,师生共同探究得到方法1,最后由学生独立探究得到方法2,这样使学生较容易地突破了本节课的难点.
1 探索勾股定理
第1课时 认识勾股定理
1.用数格子的方法探索直角三角形的三边关系,掌握勾股定理的内容.
2.让学生经历“观察—猜想—归纳—验证”的数学思维过程,体会数形结合和从特殊到一般的思想方法.
3.探索并理解直角三角形三边之间的数量关系,提高学生的推理能力.
▲重点
探索勾股定理并利用勾股定理解决问题.
▲难点
在方格纸上通过计算图形面积的方法探索勾股定理.
活动1 创设情境 导入新课(课件)
如图,从电线杆离地面8 m处向地面拉一条钢索,钢索在地面的固定点距离电线杆底部6 m,你知道需要多长的钢索吗?
直角三角形三边长度存在一种特殊的关系,这节课我们一起探索勾股定理.
活动2 实践探究 交流新知
【探究1】
1.在纸上画若干个直角三角形,分别测量它们的三边长,看看三边长的平方之间有怎样的关系?与同伴进行交流.
2.(1)观察教材图1-2中左侧的图案,正方形A中有__9__个小方格,即A的面积为__9__平方单位.(投影教材图1-2)
正方形B中有__9__个小方格,即B的面积为__9__平方单位.
正方形C中有__18__个小方格,即C的面积为__18__平方单位.
(2)你是怎样得出上面的结果的?学生思考交流并加以回答.
(3)图1-2中,A,B,C的面积之间有什么关系?
学生交流后形成共识,教师板书:SA+SB=SC.
【探究2】
我们也不难发现教材图1-2中的直角三角形是等腰直角三角形.如果不是等腰直角三角形,而是一般的直角三角形,会不会也有这种关系呢?(投影教材图1-3)
(1)教材图1-3中,A,B,C的面积是否还满足上面的关系?你是如何计算的?
答:A,B,C的面积还满足上面的关系,即SA+SB=SC,是通过数格子的方法计算的.
(2)如果直角三角形的两直角边长分别为1.6个单位长度和2.4个单位长度,上面所猜想的数量关系还成立吗?
答:仍然成立.
(3)你能发现直角三角形三边长度之间的关系吗?
【归纳】勾股定理:直角三角形两直角边的平方和等于__斜边的平方__.如果用a,b和c分别表示直角三角形的两直角边和斜边,那么__a2+b2=c2__.
活动3 开放训练 应用举例
【例1】在△ABC中,∠C=90°,a,b,c分别是∠A,∠B,∠C的对边.
(1)若a=6,b=8,求c的值;
(2)若a=5,c=13,求b的值.
【方法指导】运用勾股定理求解.
解:(1)由勾股定理,得c2=a2+b2=62+82=100.
∵102=100,
∴c=10;
(2)由勾股定理,得b2=c2-a2=132-52=144.
∵122=144,
∴b=12.
【例2】如下表,表中每行所给的三个数a,b,c,有a
32+42=52 52+122=132 72+242=252 92+402=412 ……
【方法指导】运用勾股定理a2+b2=c2,及c=b+1求解.
解:由题意,得a2+b2=c2,c=b+1.
当a=19,b=180时,c=181.
活动4 随堂练习
1.求下列图形中未知正方形的面积或未知边的长度(口答).
解:(1)400;(2)8.
2.如图,有两棵树,一棵高10 m,另一棵高4 m,两树相距8 m.一只小鸟从一棵树的树顶飞到另一棵树的树顶,则小鸟至少飞行 (B)
A.8 m B.10 m C.12 m D.14 m
3.如图所示的图形中,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为9 cm,则正方形A,B,C,D的面积的和是__81__cm2.
活动5 课堂小结与作业
学生活动:1.你这节课的主要收获是什么?
2.在探索勾股定理的过程中,我们运用了哪些方法?
教学说明:梳理本节课的重要方法和知识点,加深对本节课知识的理解.
作业:教材P3随堂练习T1、T2,P8习题1.1中的T1、T2.
这节课从探究定理、总结定理到练习的处理都是引导学生完成的,多数学生在小组活动中表现积极,找出了许多解决问题的办法,乐于与小组其他成员合作,愿意与同伴交流自己的想法,有解决问题的自信心,不回避困难,教师参与到学生的活动中,使每个同学得到了不同程度的发展.
第2课时 勾股定理的验证及其简单计算
1.掌握勾股定理及其验证,并能应用勾股定理解决一些实际问题.
2.经历勾股定理观察、猜想、验证过程,体会数形结合的思想和从特殊到一般的思想.
3.通过勾股定理解决实际问题,培养学生的探究意识和合作交流习惯.
▲重点
熟练应用拼图法验证勾股定理.
▲难点
用勾股定理解决问题.
活动1 创设情境 导入新课(课件)
据说,古埃及人曾用如图所示的方法画直角.
这种方法对吗?今天我们就来一起判断一下吧!
活动2 实践探究 交流新知
【探究1】拼图验证勾股定理
如下课件中图①是四个全等的直角三角形,两直角边分别为a和b,斜边为c.请你开动脑筋,用它们拼出一个正方形,对勾股定理进行验证.
问题1:图②中正方形ABCD的边长是__a+b__,正方形ABCD的面积可表示为__(a+b)2__.
问题2:图②中正方形ABCD由四个全等的直角三角形和一个小正方形组成,因此正方形ABCD的面积还可以表示为__4×ab+c2__.
问题3:观察两种表示方法,它们表示的是同一个图形的面积,所以结果应__相等__.
问题4:现在,你能验证勾股定理吗?
问题5:利用图③如何验证勾股定理?
【探究2】深入了解勾股定理的证法
自主探究
阅读教材P4尝试·思考.
问题1:画一个直角三角形,分别以这个直角三角形的三边为边长向外作正方形,你能利用这个图证明勾股定理的正确性吗?你是如何做的?与同伴进行交流.
合作探究
问题2:为了计算教材P4图1-4中大正方形的面积,小明对这个大正方形适当割补后,分别得到教材P4图1-5、图1-6.
(1)将所有三角形和正方形的面积用a,b,c的式子表示出来.
(2)教材图1-5、图1-6中正方形ABCD的面积分别是多少?你有哪些表示方式?
(3)你能分别利用教材图1-5、图1-6验证勾股定理吗?
解:(3)图1-5:(a+b)2=×4+c2,化简,得:a2+b2=c2;
图1-6:×4+(b-a)2=c2,化简,得:a2+b2=c2.
问题3:你能利用教材P5图1-7,1-8验证勾股定理吗?
解:图1-7:52=×4+12,即52=32+42;
图1-8:设直角三角形中,较长直角边为b,较短直角边为a,斜边长为c,则c2=×4+(b-a)2,即c2=a2+b2.
问题4:如果一个三角形是钝角三角形或锐角三角形,它的三边长能满足“较长边的平方等于另外两边的平方和”吗?
解:观察教材P6图1-10,不能满足.
【归纳】勾股定理的证明方法有300多种,必须是直角三角形的三边才能满足a2+b2=c2.
同学们可以阅读教材P6-7其他证明勾股定理的方法.
活动3 开放训练 应用举例
【例1】(教材P5例题)在一次军事演习中,红方侦察员王叔叔在距离东西向公路400 m处侦察,发现一辆蓝方汽车在公路上疾驶.他用红外测距仪测得汽车与他相距400 m;过了10 s,测得汽车与他相距500 m.你能帮王叔叔计算蓝方汽车这10 s的平均速度吗?
【方法指导】
(1)根据题意画出简单的示意图如图所示.
(2)在直角三角形中已知什么边?要求什么边?
在直角三角形中已知斜边和一条直角边,要求另一条直角边.
(3)如何计算蓝方汽车的速度?
由题意,得AC=__400_m__,AB=__500_m__,由勾股定理,得BC=__300_m__,
所以蓝方汽车这10 s的平均速度为__300÷10=30(m/s)__.
【例2】(教材P6随堂练习)如图是某沿江地区交通平面图的一部分(单位:km),为了加快经济发展,该地区拟修建一条连接M,O,Q三城市的沿江高速公路,已知沿江高速公路的建设成本是5 000万元/km,该沿江高速公路的建设成本预计是多少?
【方法指导】利用勾股定理求出斜边OM,OQ的长,再计算建设成本.
解:在Rt△MON中,由勾股定理,得OM2=MN2+NO2,
即OM2=302+402=2 500,
∴OM=50 km.
在Rt△OPQ中,由勾股定理,得OQ2=OP2+PQ2,
即OQ2=502+1202=16 900,
∴OQ=130 km,
5 000×(50+130)=900 000(万元).
答:该沿江高速公路的建设成本预计是900 000万元.
活动4 随堂练习
1.放学以后,小红和小颖分别沿着东北方向和西北方向回家,若小红和小颖行走的速度都是40 m/min,小红用15 min到家,小颖用20 min到家,小红和小颖家的距离为 (C)
A.600 m B.800 m
C.1 000 m D.不能确定
2.如图,在四边形ABCD中,∠BAD=90°,∠CBD=90°,AD=4,AB=3,BC=12,则以DC为边的正方形DCEF的面积是__169__.
3.如图,一架云梯长10 m,斜靠在一面墙上,梯子顶端离地面6 m,要使梯子顶端离地面8 m,则梯子的底部在水平方向要向左滑动__2__m.
4.如图,受某次台风的影响,一棵高18 m的大树断裂,树的顶部落在离树根底部12 m处,这棵树断裂后有多高?
解:设这棵树断裂后高x m.
根据题意,得x2+122=(18-x)2,
解得x=5.
答:这棵树断裂后高5 m.
活动5 课堂小结与作业
学生活动:谈谈本节课的收获与体会.
教学说明:学生先独立完成小结,在学生回答的过程中,老师引导学生将本节课的知识系统化.
作业:教材P8~9习题1.1中的T4、T6、T7.
勾股定理的验证既是本节课的重点,也是本节课的难点,为了突破这一难点,设计了拼图活动,先让学生从形上感知,再层层设问,从面积入手,师生共同探究得到方法1,最后由学生独立探究得到方法2,这样使学生较容易地突破了本节课的难点.
同课章节目录
