2.1 认识实数 教学设计 2025-2026学年数学北师大版八年级上册
文档属性
| 名称 | 2.1 认识实数 教学设计 2025-2026学年数学北师大版八年级上册 |

|
|
| 格式 | DOCX | ||
| 文件大小 | 78.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-20 00:00:00 | ||
图片预览

文档简介
第二章 实数
1 认识实数
第1课时 无理数的产生
1.通过拼图活动,让学生感受无理数产生的实际背景和引入的必要性.
2.通过计算器探究无理数是无限不循环小数.
3.能判断出不能用有理数表示的数.
▲重点
了解无理数与有理数的区别,并能正确判断.
▲难点
把两个边长为1的正方形剪拼成一个大正方形的动手操作过程.
活动1 创设情境 导入新课(课件)
用多媒体播放“龟免赛跑”的故事,如图,一水池呈直角三角形状,池边AC=300 m,BC=400 m,龟的速度为8 m/min,兔的速度为25 m/min,龟兔均从点C出发,龟沿CB跑.兔子沿C→A→B跑,谁先到达终点B呢?
老师:今天的龟免赛跑故事谁会取胜?
学生计算之后得出结论.
老师:它们各用多长时间?
学生:龟用50 min,免用32 min.
老师:如果我们将BC=400 m改成200 m结果会怎样?
学生先自己计算,再小组讨论,但求不出结果.
老师:为什么算不出呢?我们如果设AB=m,m2=130,你能求出m吗?它是整数吗?它是分数吗?它是有理数吗?
学生讨论之后排除整数,因为整数的平方没有等于130的;也排除分数,因为分数的平方是分数,既不是整数也不是分数,因此它不是有理数.
师:以上的例子说明我们学习的有理数已经不够用了,在日常生活中不能用有理数表示的现象还有很多,现在让我们动手体验一下吧!
活动2 实践探究 交流新知
【探究1】阅读教材P25
已知两个正方形的边长均为1,将这两个正方形进行裁剪,然后重新拼接成一个大正方形,假设新拼接后的大正方形的边长为a,则a是多少?又是怎样一个数?
(1)首先我们知道a是正方形的边长,所以从正负性来讲,a肯定是__正__数.
(2)再来看看拼接后的正方形的面积,因为两个小正方形的面积之和等于大正方形的面积,所以可以计算出新拼接后的大正方形的面积为__2__.
(3)结合12=1,22=4,那么a2=2.a是存在的.
(4)观察拼接后的图形可知,a既不是__整数__,也不是__分数__,所以a__不是__有理数.
【归纳】a在数学学习中存在,但不是有理数.
【探究2】阅读教材P25尝试·思考
(1)以直角三角形斜边为边的正方形的面积是__5__;
(2)正方形的边长为b,则b2=__22+12__;
(3)b是有理数吗?
__22<5<32,没有相同整数或分数的积等于5,b不是有理数.
【归纳】a,b都存在,但都不是有理数.
活动3 开放训练 应用举例
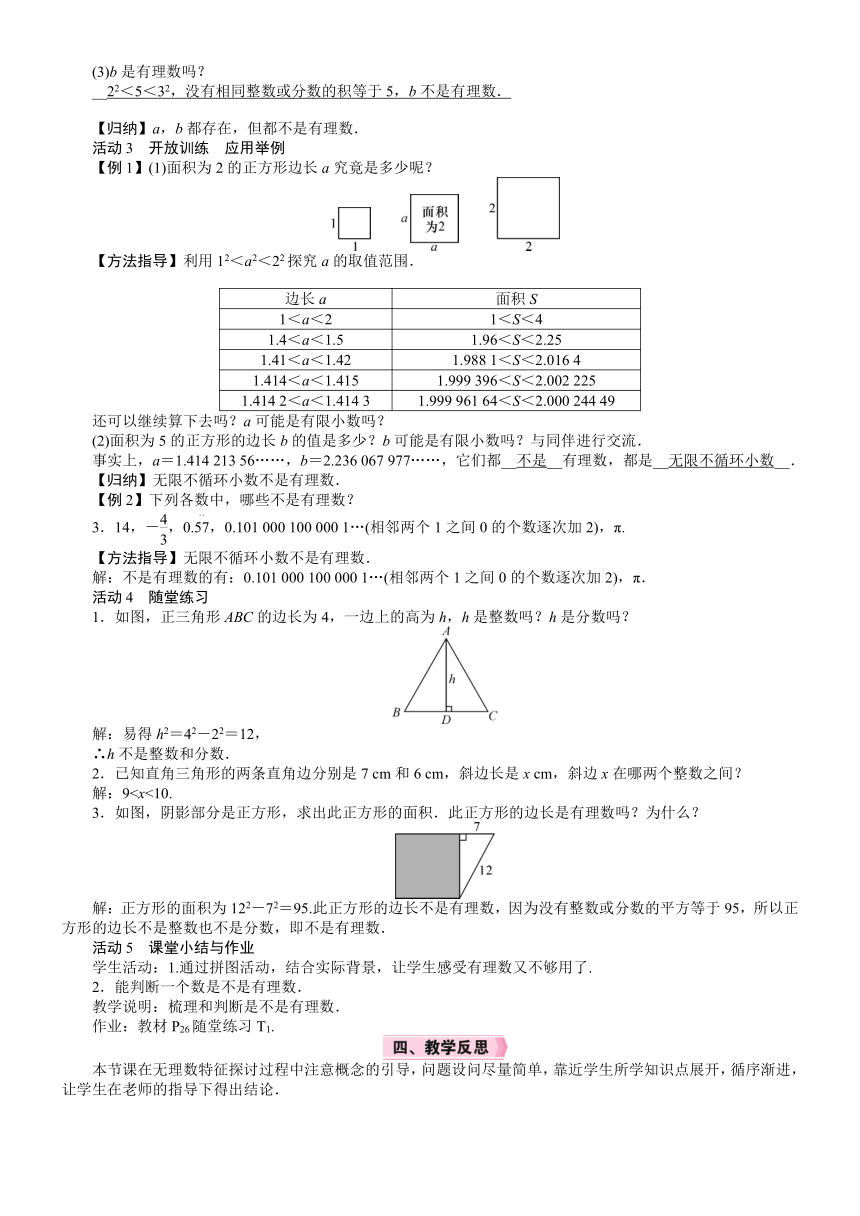
【例1】(1)面积为2的正方形边长a究竟是多少呢?
【方法指导】利用12<a2<22探究a的取值范围.
边长a 面积S
1<a<2 1<S<4
1.4<a<1.5 1.96<S<2.25
1.41<a<1.42 1.988 1<S<2.016 4
1.414<a<1.415 1.999 396<S<2.002 225
1.414 2<a<1.414 3 1.999 961 64<S<2.000 244 49
还可以继续算下去吗?a可能是有限小数吗?
(2)面积为5的正方形的边长b的值是多少?b可能是有限小数吗?与同伴进行交流.
事实上,a=1.414 213 56……,b=2.236 067 977……,它们都__不是__有理数,都是__无限不循环小数__.
【归纳】无限不循环小数不是有理数.
【例2】下列各数中,哪些不是有理数?
3.14,-,0.,0.101 000 100 000 1…(相邻两个1之间0的个数逐次加2),π.
【方法指导】无限不循环小数不是有理数.
解:不是有理数的有:0.101 000 100 000 1…(相邻两个1之间0的个数逐次加2),π.
活动4 随堂练习
1.如图,正三角形ABC的边长为4,一边上的高为h,h是整数吗?h是分数吗?
解:易得h2=42-22=12,
∴h不是整数和分数.
2.已知直角三角形的两条直角边分别是7 cm和6 cm,斜边长是x cm,斜边x在哪两个整数之间?
解:93.如图,阴影部分是正方形,求出此正方形的面积.此正方形的边长是有理数吗?为什么?
解:正方形的面积为122-72=95.此正方形的边长不是有理数,因为没有整数或分数的平方等于95,所以正方形的边长不是整数也不是分数,即不是有理数.
活动5 课堂小结与作业
学生活动:1.通过拼图活动,结合实际背景,让学生感受有理数又不够用了.
2.能判断一个数是不是有理数.
教学说明:梳理和判断是不是有理数.
作业:教材P26随堂练习T1.
本节课在无理数特征探讨过程中注意概念的引导,问题设问尽量简单,靠近学生所学知识点展开,循序渐进,让学生在老师的指导下得出结论.
第2课时 实数
1.了解实数的意义,能对实数按要求进行分类.
2.了解实数范围内,相反数、倒数、绝对值的意义.
3.用类比的方法,引入实数的运算法则、运算律,并能用这些法则、运算律在实数范围内正确计算.
▲重点
无理数和实数的意义.
▲难点
利用数轴上的点表示无理数.
活动1 创设情境 导入新课(课件)
哪些数是有理数,哪些数不是有理数:
2,,π,-,3.,,-,0,0.373 773 777 3…(相邻两个3之间的7的个数逐次加1).
有理数:{2,,-,3.,,-,0};
不是有理数:{π,0.373 773 777 3…(相邻两个3之间的7的个数逐次加1)}.
活动2 实践探究 交流新知
【探究1】实数的分类
阅读教材P26下面部分
知识归纳:__有理数__和__无理数__统称为实数.
无理数和有理数一样,也有正负之分.
分类方法:(1)实数 (2)实数
继续完成:把上题各数填到相应的集合内:
正实数集合:{ 2,,π,3.,,0.373 773 777 3…(相邻两个3之间的7的个数逐次加1), …};
负数集合:{ -,-, …};
【探究2】在实数范围内,相反数、倒数、绝对值的意义
议一议:
1.π与__-π__互为相反数,7与____互为倒数.
2.|-|=____,|0|=__0__,|-π|=__π__.
3.3-π的绝对值是__π-3__.
想一想:
(1)a是一个实数,它的相反数为__-a__,绝对值为__|a|__.
(2)如果a≠0,那么它的倒数是____.
在实数范围内,相反数、倒数、绝对值的意义与有理数范围内的相反数、倒数、绝对值的意义完全一样.实数和有理数一样,可以进行加、减、乘、除、乘方运算,而且有理数的运算法则与运算律对实数仍然适用.
【探究3】实数与数轴上的点的对应关系
(多媒体出示)教材P28图2-4,认真观察,探讨下列问题:
议一议:
两个正方形,边长分别是a,b,且满足a2=2,b2=5.
(1)如图,OA=OB,数轴上点A对应a,b中的哪个数?
(2)你能在数轴上找到另一个数对应的点吗?与同伴进行交流.
【归纳】(1)每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.也就是说,实数与数轴上的点是一一对应的.
(2)在数轴上,右边的点表示的数比左边的点表示的数大.
活动3 开放训练 应用举例
【例1】将下列各数按要求填空:-0.313 131…,,,3.14,0.482 910 200 200 02…(相邻两个2之间的0的个数逐次加1).
【方法指导】实数的分类.
有理数:__-0.313_131…,,3.14__.
无理数:__,0.482_910_200_200_02…(相邻两个2之间的0的个数逐次加1)…__.
正实数:__,,3.14,0.482_910_200_200_02…(相邻两个2之间的0的个数逐次加1)…__.
【例2】如图,数轴上表示1和a的点分别为A,B,点B关于点A的对称点是C,O为原点.
【方法指导】利用数轴表示实数.
用字母a表示线段长度:AB=__a-1__,AC=__a-1__,OC=__2-a__.
活动4 随堂练习
1.在下列实数中,无理数是 (C)
A.0 B. C. D.8
2.下列说法正确的是 (D)
A.无限小数不是有理数 B.无限小数是无理数
C.数轴上的点与有理数一一对应 D.数轴上的点与实数一一对应
3.实数a,b在数轴上对应点的位置如图所示,则下列结论正确的是 (A)
A.|a|<|b| B.a>b
C.a<-b D.|a|>|b|
4.如图,数轴上A,B分别与实数-1,1对应,用圆规在数轴上以B为圆心画点C,则与点C对应的实数是__3__.
活动5 课堂小结与作业
学生活动:这节课学习了什么知识?你的收获是什么?
教学说明:掌握实数的概念及分类、运算,会正确在数轴上表示实数.
作业:教材P28随堂练习,P29习题2.1中的T2、T3.
关注学生对实数分类的理解,同时运用类比的方法,得到对于实数的性质:相反数、绝对值、倒数和意义与有理数范围内完全一样.通过数形结合的方式,运用数轴,让学生对“实数与数轴上的点是一一对应”有更清晰的认识.
1 认识实数
第1课时 无理数的产生
1.通过拼图活动,让学生感受无理数产生的实际背景和引入的必要性.
2.通过计算器探究无理数是无限不循环小数.
3.能判断出不能用有理数表示的数.
▲重点
了解无理数与有理数的区别,并能正确判断.
▲难点
把两个边长为1的正方形剪拼成一个大正方形的动手操作过程.
活动1 创设情境 导入新课(课件)
用多媒体播放“龟免赛跑”的故事,如图,一水池呈直角三角形状,池边AC=300 m,BC=400 m,龟的速度为8 m/min,兔的速度为25 m/min,龟兔均从点C出发,龟沿CB跑.兔子沿C→A→B跑,谁先到达终点B呢?
老师:今天的龟免赛跑故事谁会取胜?
学生计算之后得出结论.
老师:它们各用多长时间?
学生:龟用50 min,免用32 min.
老师:如果我们将BC=400 m改成200 m结果会怎样?
学生先自己计算,再小组讨论,但求不出结果.
老师:为什么算不出呢?我们如果设AB=m,m2=130,你能求出m吗?它是整数吗?它是分数吗?它是有理数吗?
学生讨论之后排除整数,因为整数的平方没有等于130的;也排除分数,因为分数的平方是分数,既不是整数也不是分数,因此它不是有理数.
师:以上的例子说明我们学习的有理数已经不够用了,在日常生活中不能用有理数表示的现象还有很多,现在让我们动手体验一下吧!
活动2 实践探究 交流新知
【探究1】阅读教材P25
已知两个正方形的边长均为1,将这两个正方形进行裁剪,然后重新拼接成一个大正方形,假设新拼接后的大正方形的边长为a,则a是多少?又是怎样一个数?
(1)首先我们知道a是正方形的边长,所以从正负性来讲,a肯定是__正__数.
(2)再来看看拼接后的正方形的面积,因为两个小正方形的面积之和等于大正方形的面积,所以可以计算出新拼接后的大正方形的面积为__2__.
(3)结合12=1,22=4,那么a2=2.a是存在的.
(4)观察拼接后的图形可知,a既不是__整数__,也不是__分数__,所以a__不是__有理数.
【归纳】a在数学学习中存在,但不是有理数.
【探究2】阅读教材P25尝试·思考
(1)以直角三角形斜边为边的正方形的面积是__5__;
(2)正方形的边长为b,则b2=__22+12__;
(3)b是有理数吗?
__22<5<32,没有相同整数或分数的积等于5,b不是有理数.
【归纳】a,b都存在,但都不是有理数.
活动3 开放训练 应用举例
【例1】(1)面积为2的正方形边长a究竟是多少呢?
【方法指导】利用12<a2<22探究a的取值范围.
边长a 面积S
1<a<2 1<S<4
1.4<a<1.5 1.96<S<2.25
1.41<a<1.42 1.988 1<S<2.016 4
1.414<a<1.415 1.999 396<S<2.002 225
1.414 2<a<1.414 3 1.999 961 64<S<2.000 244 49
还可以继续算下去吗?a可能是有限小数吗?
(2)面积为5的正方形的边长b的值是多少?b可能是有限小数吗?与同伴进行交流.
事实上,a=1.414 213 56……,b=2.236 067 977……,它们都__不是__有理数,都是__无限不循环小数__.
【归纳】无限不循环小数不是有理数.
【例2】下列各数中,哪些不是有理数?
3.14,-,0.,0.101 000 100 000 1…(相邻两个1之间0的个数逐次加2),π.
【方法指导】无限不循环小数不是有理数.
解:不是有理数的有:0.101 000 100 000 1…(相邻两个1之间0的个数逐次加2),π.
活动4 随堂练习
1.如图,正三角形ABC的边长为4,一边上的高为h,h是整数吗?h是分数吗?
解:易得h2=42-22=12,
∴h不是整数和分数.
2.已知直角三角形的两条直角边分别是7 cm和6 cm,斜边长是x cm,斜边x在哪两个整数之间?
解:9
解:正方形的面积为122-72=95.此正方形的边长不是有理数,因为没有整数或分数的平方等于95,所以正方形的边长不是整数也不是分数,即不是有理数.
活动5 课堂小结与作业
学生活动:1.通过拼图活动,结合实际背景,让学生感受有理数又不够用了.
2.能判断一个数是不是有理数.
教学说明:梳理和判断是不是有理数.
作业:教材P26随堂练习T1.
本节课在无理数特征探讨过程中注意概念的引导,问题设问尽量简单,靠近学生所学知识点展开,循序渐进,让学生在老师的指导下得出结论.
第2课时 实数
1.了解实数的意义,能对实数按要求进行分类.
2.了解实数范围内,相反数、倒数、绝对值的意义.
3.用类比的方法,引入实数的运算法则、运算律,并能用这些法则、运算律在实数范围内正确计算.
▲重点
无理数和实数的意义.
▲难点
利用数轴上的点表示无理数.
活动1 创设情境 导入新课(课件)
哪些数是有理数,哪些数不是有理数:
2,,π,-,3.,,-,0,0.373 773 777 3…(相邻两个3之间的7的个数逐次加1).
有理数:{2,,-,3.,,-,0};
不是有理数:{π,0.373 773 777 3…(相邻两个3之间的7的个数逐次加1)}.
活动2 实践探究 交流新知
【探究1】实数的分类
阅读教材P26下面部分
知识归纳:__有理数__和__无理数__统称为实数.
无理数和有理数一样,也有正负之分.
分类方法:(1)实数 (2)实数
继续完成:把上题各数填到相应的集合内:
正实数集合:{ 2,,π,3.,,0.373 773 777 3…(相邻两个3之间的7的个数逐次加1), …};
负数集合:{ -,-, …};
【探究2】在实数范围内,相反数、倒数、绝对值的意义
议一议:
1.π与__-π__互为相反数,7与____互为倒数.
2.|-|=____,|0|=__0__,|-π|=__π__.
3.3-π的绝对值是__π-3__.
想一想:
(1)a是一个实数,它的相反数为__-a__,绝对值为__|a|__.
(2)如果a≠0,那么它的倒数是____.
在实数范围内,相反数、倒数、绝对值的意义与有理数范围内的相反数、倒数、绝对值的意义完全一样.实数和有理数一样,可以进行加、减、乘、除、乘方运算,而且有理数的运算法则与运算律对实数仍然适用.
【探究3】实数与数轴上的点的对应关系
(多媒体出示)教材P28图2-4,认真观察,探讨下列问题:
议一议:
两个正方形,边长分别是a,b,且满足a2=2,b2=5.
(1)如图,OA=OB,数轴上点A对应a,b中的哪个数?
(2)你能在数轴上找到另一个数对应的点吗?与同伴进行交流.
【归纳】(1)每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数.也就是说,实数与数轴上的点是一一对应的.
(2)在数轴上,右边的点表示的数比左边的点表示的数大.
活动3 开放训练 应用举例
【例1】将下列各数按要求填空:-0.313 131…,,,3.14,0.482 910 200 200 02…(相邻两个2之间的0的个数逐次加1).
【方法指导】实数的分类.
有理数:__-0.313_131…,,3.14__.
无理数:__,0.482_910_200_200_02…(相邻两个2之间的0的个数逐次加1)…__.
正实数:__,,3.14,0.482_910_200_200_02…(相邻两个2之间的0的个数逐次加1)…__.
【例2】如图,数轴上表示1和a的点分别为A,B,点B关于点A的对称点是C,O为原点.
【方法指导】利用数轴表示实数.
用字母a表示线段长度:AB=__a-1__,AC=__a-1__,OC=__2-a__.
活动4 随堂练习
1.在下列实数中,无理数是 (C)
A.0 B. C. D.8
2.下列说法正确的是 (D)
A.无限小数不是有理数 B.无限小数是无理数
C.数轴上的点与有理数一一对应 D.数轴上的点与实数一一对应
3.实数a,b在数轴上对应点的位置如图所示,则下列结论正确的是 (A)
A.|a|<|b| B.a>b
C.a<-b D.|a|>|b|
4.如图,数轴上A,B分别与实数-1,1对应,用圆规在数轴上以B为圆心画点C,则与点C对应的实数是__3__.
活动5 课堂小结与作业
学生活动:这节课学习了什么知识?你的收获是什么?
教学说明:掌握实数的概念及分类、运算,会正确在数轴上表示实数.
作业:教材P28随堂练习,P29习题2.1中的T2、T3.
关注学生对实数分类的理解,同时运用类比的方法,得到对于实数的性质:相反数、绝对值、倒数和意义与有理数范围内完全一样.通过数形结合的方式,运用数轴,让学生对“实数与数轴上的点是一一对应”有更清晰的认识.
同课章节目录
