27.3位似(巩固复习.培优卷.含解析)-2024-2025学年人教版(2024)数学九年级下册
文档属性
| 名称 | 27.3位似(巩固复习.培优卷.含解析)-2024-2025学年人教版(2024)数学九年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 363.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-21 15:59:53 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
巩固复习.培优卷 位似
一.选择题(共5小题)
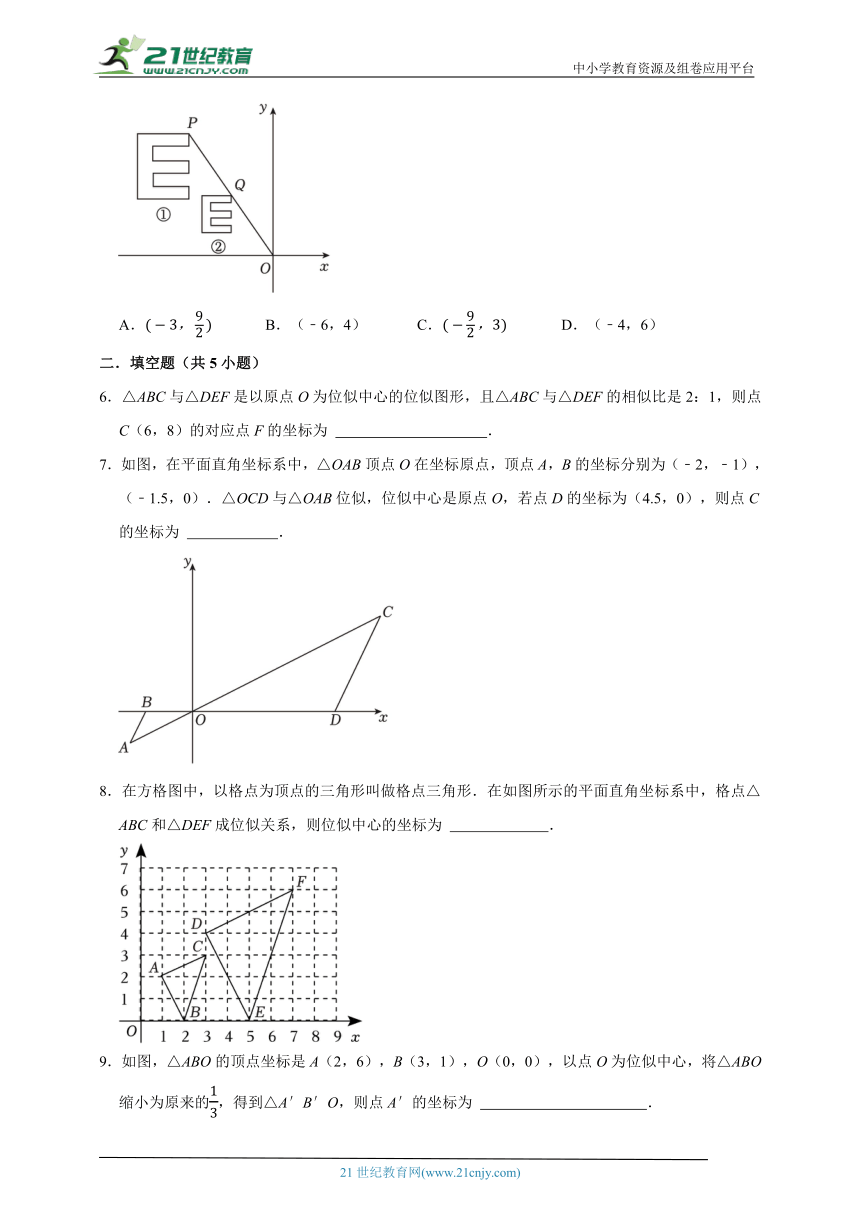
1.如图,△ABC与△DEF位似,位似中心为点O,若OA:AD=1:2,△ABC的周长为3,则△DEF的周长为( )
A.6 B.9 C.12 D.27
2.如图,在平面直角坐标系中,△ABC与△DEF是以坐标原点O为位似中心的位似图形,若A(﹣2,0),D(3,0),且AC,则线段DF的长度为( )
A. B. C. D.
3.如图,已知△ABC与△DEF位似,位似中心为O,且△ABC与△DEF的周长之比是4:3,则AO:DO的值为( )
A.4:7 B.4:3 C.3:4 D.16:9
4.已知关于原点位似的两个图形上,一组对应点的坐标分别为(1,﹣2)和(﹣2,x),则x=( )
A.1 B.﹣1 C.4 D.﹣4
5.如图,将视力表中的两个“E”放在平面直角坐标系中,两个“E”字是位似图形,位似中心点O,①号“E”与②号“E”的相似比为2:1.点P与Q为一组对应点,若点Q坐标为(﹣2,3),则点P的坐标为( )
A. B.(﹣6,4) C. D.(﹣4,6)
二.填空题(共5小题)
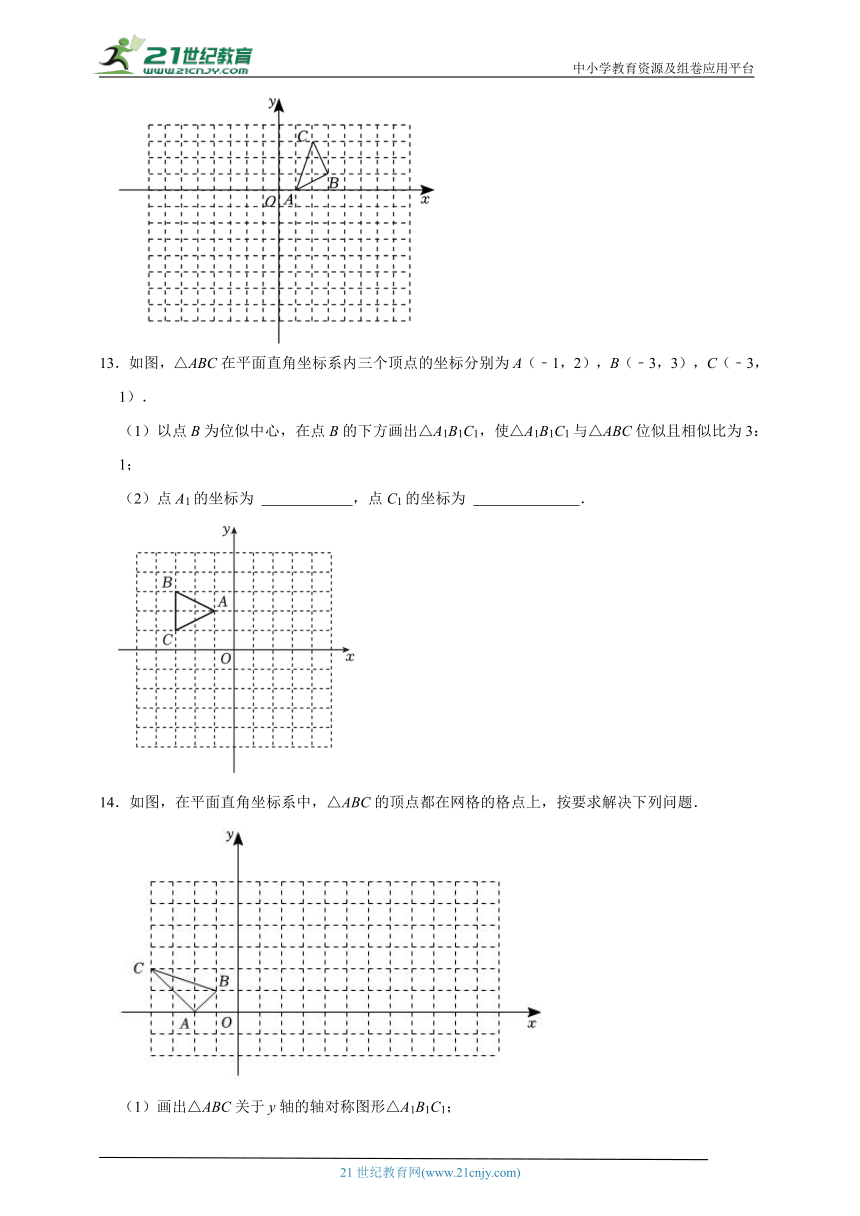
6.△ABC与△DEF是以原点O为位似中心的位似图形,且△ABC与△DEF的相似比是2:1,则点C(6,8)的对应点F的坐标为 .
7.如图,在平面直角坐标系中,△OAB顶点O在坐标原点,顶点A,B的坐标分别为(﹣2,﹣1),(﹣1.5,0).△OCD与△OAB位似,位似中心是原点O,若点D的坐标为(4.5,0),则点C的坐标为 .
8.在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点△ABC和△DEF成位似关系,则位似中心的坐标为 .
9.如图,△ABO的顶点坐标是A(2,6),B(3,1),O(0,0),以点O为位似中心,将△ABO缩小为原来的,得到△A′B′O,则点A′的坐标为 .
10.如图,△ABC和△DEF是以点O为位似中心的位似图形,相似比为2:3,则△ABC和△DEF的面积比是 .
三.解答题(共5小题)
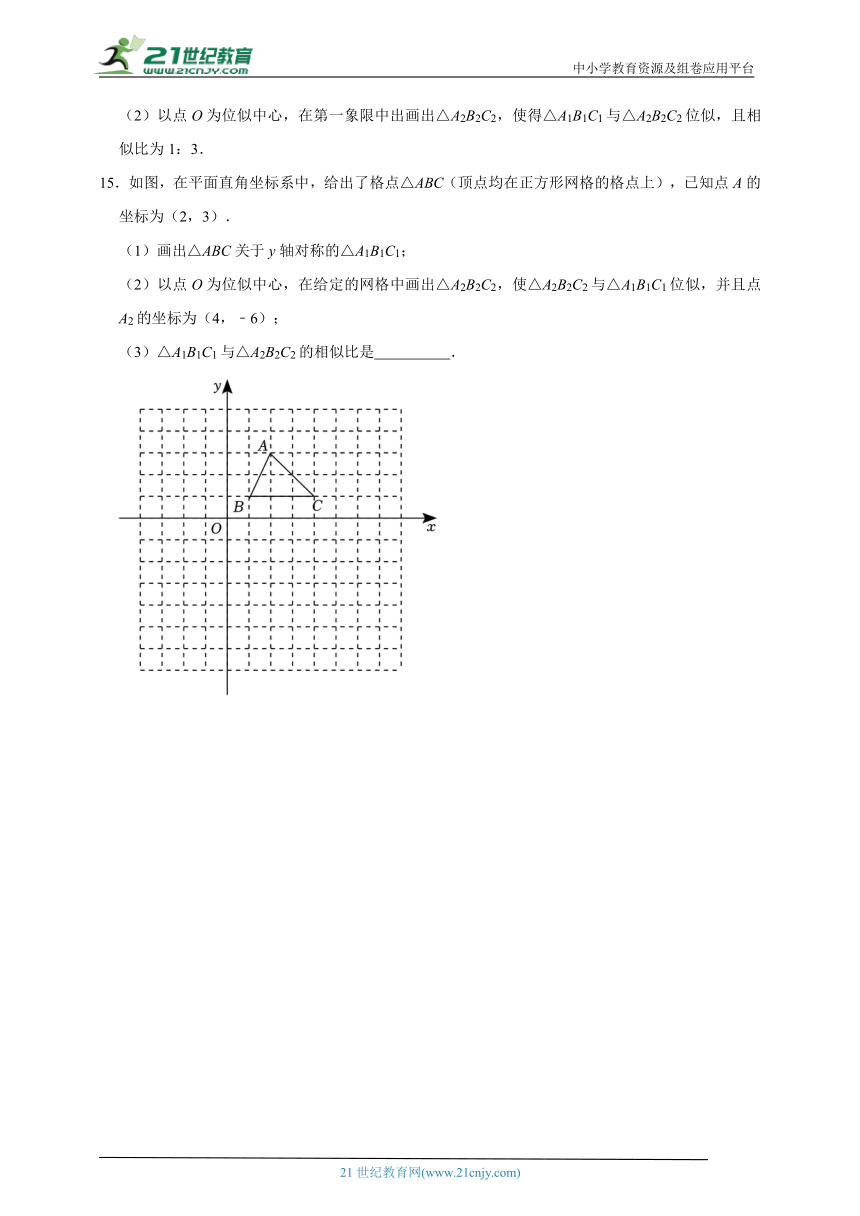
11.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点的坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
12.如图所示,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,0),B(3,1),C(2,3).请在所给直角坐标系中按要求画图和解答下列问题:
(1)画出△ABC关于x轴成轴对称的△A1B1C1,并直接写出点B1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△ABC的位似三角形△A2B2C2,使它与△ABC的相似比为2:1,并写出点C2的坐标.
13.如图,△ABC在平面直角坐标系内三个顶点的坐标分别为A(﹣1,2),B(﹣3,3),C(﹣3,1).
(1)以点B为位似中心,在点B的下方画出△A1B1C1,使△A1B1C1与△ABC位似且相似比为3:1;
(2)点A1的坐标为 ,点C1的坐标为 .
14.如图,在平面直角坐标系中,△ABC的顶点都在网格的格点上,按要求解决下列问题.
(1)画出△ABC关于y轴的轴对称图形△A1B1C1;
(2)以点O为位似中心,在第一象限中出画出△A2B2C2,使得△A1B1C1与△A2B2C2位似,且相似比为1:3.
15.如图,在平面直角坐标系中,给出了格点△ABC(顶点均在正方形网格的格点上),已知点A的坐标为(2,3).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)以点O为位似中心,在给定的网格中画出△A2B2C2,使△A2B2C2与△A1B1C1位似,并且点A2的坐标为(4,﹣6);
(3)△A1B1C1与△A2B2C2的相似比是 .
巩固复习.培优卷 位似
参考答案与试题解析
一.选择题(共5小题)
1.如图,△ABC与△DEF位似,位似中心为点O,若OA:AD=1:2,△ABC的周长为3,则△DEF的周长为( )
A.6 B.9 C.12 D.27
【考点】位似变换.
【专题】图形的相似;运算能力.
【答案】B
【分析】利用位似的性质得△ABC∽△DEF,AC:DF=OA:OD=1:3,然后根据相似三角形的性质解决问题.
【解答】解:∵△ABC与△DEF位似,点O为位似中心.OA:AD=1:2,
∴△ABC∽△DEF,AC:DF=OA:OD=1:3,
∴△ABC的周长:△DEF的周长=1:3,
∴△DEF的周长为3×3=9.
故选:B.
【点评】本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.位似图形必须是相似形,对应点的连线都经过同一点;对应边平行或共线.
2.如图,在平面直角坐标系中,△ABC与△DEF是以坐标原点O为位似中心的位似图形,若A(﹣2,0),D(3,0),且AC,则线段DF的长度为( )
A. B. C. D.
【考点】位似变换;坐标与图形性质.
【专题】图形的相似;推理能力.
【答案】B
【分析】根据题意求出相似比,计算即可.
【解答】解:∵△ABC与△DEF是以坐标原点O为位似中心的位似图形,A(﹣2,0),D(3,0),
∴△ABC∽△DEF,且相似比为2:3,
∴,
∵AC=2,
∴DF=3,
故选:B.
【点评】本题考查的是位似变换,根据题意求出相似比是解题的关键.
3.如图,已知△ABC与△DEF位似,位似中心为O,且△ABC与△DEF的周长之比是4:3,则AO:DO的值为( )
A.4:7 B.4:3 C.3:4 D.16:9
【考点】位似变换.
【专题】图形的相似;推理能力.
【答案】B
【分析】根据位似图形的概念得到△ABC∽△DEF,AB∥DE,根据相似三角形的性质求出AB:DE=4:3,再根据相似三角形的性质计算即可.
【解答】解:∵△ABC与△DEF位似,
∴△ABC∽△DEF,AB∥DE,
∵△ABC与△DEF的周长之比是4:3,
∴AB:DE=4:3,
∵AB∥DE,
∴△AOB∽△DOE,
∴AO:DO=AB:DE=4:3,
故选:B.
【点评】本题考查的是位似变换、相似三角形的性质,熟记相似三角形的周长比等于相似比是解题的关键.
4.已知关于原点位似的两个图形上,一组对应点的坐标分别为(1,﹣2)和(﹣2,x),则x=( )
A.1 B.﹣1 C.4 D.﹣4
【考点】位似变换;坐标与图形性质.
【专题】图形的相似;推理能力.
【答案】C
【分析】根据位似变换的性质列出比例式,计算即可.
【解答】解:∵两个图形关于原点位似,一组对应点的坐标分别为(1,﹣2)和(﹣2,x),
∴,
解得:x=4,
故选:C.
【点评】本题考查的是位似变换,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
5.如图,将视力表中的两个“E”放在平面直角坐标系中,两个“E”字是位似图形,位似中心点O,①号“E”与②号“E”的相似比为2:1.点P与Q为一组对应点,若点Q坐标为(﹣2,3),则点P的坐标为( )
A. B.(﹣6,4) C. D.(﹣4,6)
【考点】位似变换;坐标确定位置.
【专题】图形的相似;推理能力.
【答案】D
【分析】根据位似变换的性质计算,将Q点的横、纵坐标乘以2,即可求解.
【解答】解:∵①号“E”与②号“E”的相似比为2:1,点Q坐标为(﹣2,3)
∴点P的坐标为(﹣2×2,3×2),即(﹣4,6),
故选:D.
【点评】此题考查了位似变换的性质:如果两个图形位似,那么任意一对对应点到位似中心的距离之比都等于位似比,任意一组对应边都互相平行(或在一条直线上),熟记性质是解题的关键.
二.填空题(共5小题)
6.△ABC与△DEF是以原点O为位似中心的位似图形,且△ABC与△DEF的相似比是2:1,则点C(6,8)的对应点F的坐标为 (3,4)或(﹣3,﹣4) .
【考点】位似变换;坐标与图形性质.
【专题】图形的相似;推理能力.
【答案】见试题解答内容
【分析】根据位似变换的性质解答即可.
【解答】解:∵△ABC与△DEF是以原点O为位似中心的位似图形,相似比是2:1,点C(6,8),
∴点C的对应点F的坐标为(6,8)或(6×(),8×()),即(3,4)或(﹣3,﹣4),
故答案为:(3,4)或(﹣3,﹣4).
【点评】本题考查的是位似变换,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
7.如图,在平面直角坐标系中,△OAB顶点O在坐标原点,顶点A,B的坐标分别为(﹣2,﹣1),(﹣1.5,0).△OCD与△OAB位似,位似中心是原点O,若点D的坐标为(4.5,0),则点C的坐标为 (6,3) .
【考点】位似变换;坐标与图形性质.
【专题】图形的相似;推理能力.
【答案】(6,3).
【分析】根据题意求出△OCD与△OAB的相似比,再根据位似变换的性质计算即可.
【解答】解:∵△OCD与△OAB位似,位似中心是原点O,点B的坐标为(﹣1.5,0),点D的坐标为(4.5,0),
∴△OCD与△OAB的相似比为3:1,
∵点A的坐标为(﹣2,﹣1),
∴点C的坐标为(﹣2×(﹣3),﹣1×(﹣3)),即(6,3),
故答案为:(6,3).
【点评】本题考查的是位似变换,正确求出相似比是解题的关键.
8.在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点△ABC和△DEF成位似关系,则位似中心的坐标为 (﹣1,0) .
【考点】位似变换;坐标与图形性质.
【专题】图形的相似;推理能力.
【答案】(﹣1,0).
【分析】利用待定系数法求出直线AD的解析式,根据位似中心的概念解答即可.
【解答】解:设直线AD的解析式为y=kx+b,
∵点A的坐标为(1,2),点D的坐标为(3,4),
∴,
解得:,
∴直线AD的解析式为y=x+1,
由位似图形的概念可知:△ABC与△DEF的位似中心是直线AD与直线BE的交点,
∵直线y=x+1与x轴的交点是(﹣1,0),
∴位似中心的坐标为(﹣1,0).
【点评】本题考查的是位似图形的概念、待定系数法求一次函数解析式,掌握位似中心的概念是解题的关键.
9.如图,△ABO的顶点坐标是A(2,6),B(3,1),O(0,0),以点O为位似中心,将△ABO缩小为原来的,得到△A′B′O,则点A′的坐标为 (,2)或(,﹣2) .
【考点】位似变换;坐标与图形性质.
【专题】图形的相似;运算能力.
【答案】(,2)或(,﹣2).
【分析】根据位似变换的性质计算,得到答案.
【解答】解:∵以原点O为位似中心,把△ABC缩小为原来的,可以得到△A'B'O,点A的坐标为(2,6),
∴点A'的坐标是(2,6)或(2×(),6×()),即(,2)或(,﹣2).
故答案为:(,2)或(,﹣2).
【点评】本题考查的是位似变换的性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
10.如图,△ABC和△DEF是以点O为位似中心的位似图形,相似比为2:3,则△ABC和△DEF的面积比是 4:9 .
【考点】位似变换.
【专题】图形的相似;运算能力.
【答案】4:9.
【分析】先利用位似的性质得到△ABC∽△DEF,相似比为2:3,然后根据相似三角形的性质解决问题.
【解答】解:∵△ABC与△DEF是以点O为位似中心的位似图形,位似比为2:3,
∴△ABC∽△DEF,相似比为2:3,
∴△ABC与△DEF的面积之比为22:32=4:9.
故答案为:4:9.
【点评】本题考查的是位似变换的概念和性质、相似三角形的性质,熟记相似三角形的面积比等于相似比的平方是解题的关键.
三.解答题(共5小题)
11.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点的坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
【考点】作图﹣位似变换;作图﹣轴对称变换.
【专题】平移、旋转与对称;图形的相似;几何直观.
【答案】(1)△A1B1C1见解答,(3,2);
(2)△A2B2C2见解答,(﹣6,4).
【分析】(1)分别作出三个顶点关于y轴的对称点,再首尾顺次连接即可;
(2)根据位似图形的概念作出三个顶点的对应点,再首尾顺次连接即可.
【解答】解:(1)如图所示,△A1B1C1即为所求,
由图知,C1点的坐标为(3,2);
(2)如图所示,△A2B2C2即为所求,C2点坐标为(﹣6,4).
【点评】本题主要考查作图—轴对称变换与位似变换,解题的关键是掌握轴对称变换与位似变换的定义与性质,并据此得出变换后的对应点.
12.如图所示,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,0),B(3,1),C(2,3).请在所给直角坐标系中按要求画图和解答下列问题:
(1)画出△ABC关于x轴成轴对称的△A1B1C1,并直接写出点B1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△ABC的位似三角形△A2B2C2,使它与△ABC的相似比为2:1,并写出点C2的坐标.
【考点】作图﹣位似变换;作图﹣轴对称变换.
【专题】平移、旋转与对称;图形的相似;几何直观.
【答案】(1)画图见解答;B1(3,﹣1).
(2)画图见解答;C2(﹣4,﹣6).
【分析】(1)根据轴对称的性质作图,即可得出答案.
(2)根据位似的性质作图,即可得出答案.
【解答】解:(1)如图,△A1B1C1即为所求.
点B1的坐标为(3,﹣1).
(2)如图,△A2B2C2即为所求.
点C2的坐标为(﹣4,﹣6).
【点评】本题考查作图﹣轴对称变换、位似变换,熟练掌握轴对称的性质、位似的性质是解答本题的关键.
13.如图,△ABC在平面直角坐标系内三个顶点的坐标分别为A(﹣1,2),B(﹣3,3),C(﹣3,1).
(1)以点B为位似中心,在点B的下方画出△A1B1C1,使△A1B1C1与△ABC位似且相似比为3:1;
(2)点A1的坐标为 (3,0) ,点C1的坐标为 (﹣3,﹣3) .
【考点】作图﹣位似变换;点的坐标.
【专题】作图题;图形的相似;几何直观.
【答案】(1)见解析;
(2)(3,0),(﹣3,﹣3).
【分析】(1)在网格中作出A1、C1,连接A1C1、BC1、BA1即可得到△A1B1C1;
(2)根据点的位置写出A1、A1、C1的坐标即可.
【解答】解:(1)△A1B1C1即为所作;
(2)点A1的坐标为(3,0),点C1的坐标为(﹣3,﹣3),
故答案为:(3,0),(﹣3,﹣3).
【点评】本题考查了位似作图,图形与坐标,掌握位似的性质是解题的关键.
14.如图,在平面直角坐标系中,△ABC的顶点都在网格的格点上,按要求解决下列问题.
(1)画出△ABC关于y轴的轴对称图形△A1B1C1;
(2)以点O为位似中心,在第一象限中出画出△A2B2C2,使得△A1B1C1与△A2B2C2位似,且相似比为1:3.
【考点】作图﹣位似变换;作图﹣轴对称变换.
【专题】平移、旋转与对称;图形的相似;几何直观;推理能力.
【答案】(1)作图见解析过程;
(2)作图见解析过程.
【分析】(1)分别得出点A、B、C关于y轴的对称点,然后连线即可;
(2)由(1)及位似的性质进行作图即可.
【解答】解:(1)如图1所示,△A1B1C1即为所求.
(2)如图2所示,△A2B2C2即为所求.
【点评】本题主要考查轴对称及位似,熟练掌握轴对称及位似的性质是解题的关键.
15.如图,在平面直角坐标系中,给出了格点△ABC(顶点均在正方形网格的格点上),已知点A的坐标为(2,3).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)以点O为位似中心,在给定的网格中画出△A2B2C2,使△A2B2C2与△A1B1C1位似,并且点A2的坐标为(4,﹣6);
(3)△A1B1C1与△A2B2C2的相似比是 1:2 .
【考点】作图﹣位似变换;作图﹣轴对称变换.
【专题】作图题;平移、旋转与对称;几何直观.
【答案】(1)见解析;
(2)见解析;
(3)1:2.
【分析】(1)根据轴对称的性质作出图形即可;
(2)利用点A和A2的坐标特征得到位似比,再把B、C的横纵坐标都乘以2得到B2、C2的坐标,然后描点即可;
(3)根据相似三角形的性质即可得到结论.
【解答】解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)∵△A1B1C1∽△A2B2C2,C1B1=3,C2B2=6
∴△A1B1C1与△A2B2C2的相似比1:2,
故答案为:1:2.
【点评】此题主要考查了作图﹣位似变换以及关于y轴对称点的性质,正确得出对应点位置是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
巩固复习.培优卷 位似
一.选择题(共5小题)
1.如图,△ABC与△DEF位似,位似中心为点O,若OA:AD=1:2,△ABC的周长为3,则△DEF的周长为( )
A.6 B.9 C.12 D.27
2.如图,在平面直角坐标系中,△ABC与△DEF是以坐标原点O为位似中心的位似图形,若A(﹣2,0),D(3,0),且AC,则线段DF的长度为( )
A. B. C. D.
3.如图,已知△ABC与△DEF位似,位似中心为O,且△ABC与△DEF的周长之比是4:3,则AO:DO的值为( )
A.4:7 B.4:3 C.3:4 D.16:9
4.已知关于原点位似的两个图形上,一组对应点的坐标分别为(1,﹣2)和(﹣2,x),则x=( )
A.1 B.﹣1 C.4 D.﹣4
5.如图,将视力表中的两个“E”放在平面直角坐标系中,两个“E”字是位似图形,位似中心点O,①号“E”与②号“E”的相似比为2:1.点P与Q为一组对应点,若点Q坐标为(﹣2,3),则点P的坐标为( )
A. B.(﹣6,4) C. D.(﹣4,6)
二.填空题(共5小题)
6.△ABC与△DEF是以原点O为位似中心的位似图形,且△ABC与△DEF的相似比是2:1,则点C(6,8)的对应点F的坐标为 .
7.如图,在平面直角坐标系中,△OAB顶点O在坐标原点,顶点A,B的坐标分别为(﹣2,﹣1),(﹣1.5,0).△OCD与△OAB位似,位似中心是原点O,若点D的坐标为(4.5,0),则点C的坐标为 .
8.在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点△ABC和△DEF成位似关系,则位似中心的坐标为 .
9.如图,△ABO的顶点坐标是A(2,6),B(3,1),O(0,0),以点O为位似中心,将△ABO缩小为原来的,得到△A′B′O,则点A′的坐标为 .
10.如图,△ABC和△DEF是以点O为位似中心的位似图形,相似比为2:3,则△ABC和△DEF的面积比是 .
三.解答题(共5小题)
11.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点的坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
12.如图所示,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,0),B(3,1),C(2,3).请在所给直角坐标系中按要求画图和解答下列问题:
(1)画出△ABC关于x轴成轴对称的△A1B1C1,并直接写出点B1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△ABC的位似三角形△A2B2C2,使它与△ABC的相似比为2:1,并写出点C2的坐标.
13.如图,△ABC在平面直角坐标系内三个顶点的坐标分别为A(﹣1,2),B(﹣3,3),C(﹣3,1).
(1)以点B为位似中心,在点B的下方画出△A1B1C1,使△A1B1C1与△ABC位似且相似比为3:1;
(2)点A1的坐标为 ,点C1的坐标为 .
14.如图,在平面直角坐标系中,△ABC的顶点都在网格的格点上,按要求解决下列问题.
(1)画出△ABC关于y轴的轴对称图形△A1B1C1;
(2)以点O为位似中心,在第一象限中出画出△A2B2C2,使得△A1B1C1与△A2B2C2位似,且相似比为1:3.
15.如图,在平面直角坐标系中,给出了格点△ABC(顶点均在正方形网格的格点上),已知点A的坐标为(2,3).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)以点O为位似中心,在给定的网格中画出△A2B2C2,使△A2B2C2与△A1B1C1位似,并且点A2的坐标为(4,﹣6);
(3)△A1B1C1与△A2B2C2的相似比是 .
巩固复习.培优卷 位似
参考答案与试题解析
一.选择题(共5小题)
1.如图,△ABC与△DEF位似,位似中心为点O,若OA:AD=1:2,△ABC的周长为3,则△DEF的周长为( )
A.6 B.9 C.12 D.27
【考点】位似变换.
【专题】图形的相似;运算能力.
【答案】B
【分析】利用位似的性质得△ABC∽△DEF,AC:DF=OA:OD=1:3,然后根据相似三角形的性质解决问题.
【解答】解:∵△ABC与△DEF位似,点O为位似中心.OA:AD=1:2,
∴△ABC∽△DEF,AC:DF=OA:OD=1:3,
∴△ABC的周长:△DEF的周长=1:3,
∴△DEF的周长为3×3=9.
故选:B.
【点评】本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.位似图形必须是相似形,对应点的连线都经过同一点;对应边平行或共线.
2.如图,在平面直角坐标系中,△ABC与△DEF是以坐标原点O为位似中心的位似图形,若A(﹣2,0),D(3,0),且AC,则线段DF的长度为( )
A. B. C. D.
【考点】位似变换;坐标与图形性质.
【专题】图形的相似;推理能力.
【答案】B
【分析】根据题意求出相似比,计算即可.
【解答】解:∵△ABC与△DEF是以坐标原点O为位似中心的位似图形,A(﹣2,0),D(3,0),
∴△ABC∽△DEF,且相似比为2:3,
∴,
∵AC=2,
∴DF=3,
故选:B.
【点评】本题考查的是位似变换,根据题意求出相似比是解题的关键.
3.如图,已知△ABC与△DEF位似,位似中心为O,且△ABC与△DEF的周长之比是4:3,则AO:DO的值为( )
A.4:7 B.4:3 C.3:4 D.16:9
【考点】位似变换.
【专题】图形的相似;推理能力.
【答案】B
【分析】根据位似图形的概念得到△ABC∽△DEF,AB∥DE,根据相似三角形的性质求出AB:DE=4:3,再根据相似三角形的性质计算即可.
【解答】解:∵△ABC与△DEF位似,
∴△ABC∽△DEF,AB∥DE,
∵△ABC与△DEF的周长之比是4:3,
∴AB:DE=4:3,
∵AB∥DE,
∴△AOB∽△DOE,
∴AO:DO=AB:DE=4:3,
故选:B.
【点评】本题考查的是位似变换、相似三角形的性质,熟记相似三角形的周长比等于相似比是解题的关键.
4.已知关于原点位似的两个图形上,一组对应点的坐标分别为(1,﹣2)和(﹣2,x),则x=( )
A.1 B.﹣1 C.4 D.﹣4
【考点】位似变换;坐标与图形性质.
【专题】图形的相似;推理能力.
【答案】C
【分析】根据位似变换的性质列出比例式,计算即可.
【解答】解:∵两个图形关于原点位似,一组对应点的坐标分别为(1,﹣2)和(﹣2,x),
∴,
解得:x=4,
故选:C.
【点评】本题考查的是位似变换,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
5.如图,将视力表中的两个“E”放在平面直角坐标系中,两个“E”字是位似图形,位似中心点O,①号“E”与②号“E”的相似比为2:1.点P与Q为一组对应点,若点Q坐标为(﹣2,3),则点P的坐标为( )
A. B.(﹣6,4) C. D.(﹣4,6)
【考点】位似变换;坐标确定位置.
【专题】图形的相似;推理能力.
【答案】D
【分析】根据位似变换的性质计算,将Q点的横、纵坐标乘以2,即可求解.
【解答】解:∵①号“E”与②号“E”的相似比为2:1,点Q坐标为(﹣2,3)
∴点P的坐标为(﹣2×2,3×2),即(﹣4,6),
故选:D.
【点评】此题考查了位似变换的性质:如果两个图形位似,那么任意一对对应点到位似中心的距离之比都等于位似比,任意一组对应边都互相平行(或在一条直线上),熟记性质是解题的关键.
二.填空题(共5小题)
6.△ABC与△DEF是以原点O为位似中心的位似图形,且△ABC与△DEF的相似比是2:1,则点C(6,8)的对应点F的坐标为 (3,4)或(﹣3,﹣4) .
【考点】位似变换;坐标与图形性质.
【专题】图形的相似;推理能力.
【答案】见试题解答内容
【分析】根据位似变换的性质解答即可.
【解答】解:∵△ABC与△DEF是以原点O为位似中心的位似图形,相似比是2:1,点C(6,8),
∴点C的对应点F的坐标为(6,8)或(6×(),8×()),即(3,4)或(﹣3,﹣4),
故答案为:(3,4)或(﹣3,﹣4).
【点评】本题考查的是位似变换,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
7.如图,在平面直角坐标系中,△OAB顶点O在坐标原点,顶点A,B的坐标分别为(﹣2,﹣1),(﹣1.5,0).△OCD与△OAB位似,位似中心是原点O,若点D的坐标为(4.5,0),则点C的坐标为 (6,3) .
【考点】位似变换;坐标与图形性质.
【专题】图形的相似;推理能力.
【答案】(6,3).
【分析】根据题意求出△OCD与△OAB的相似比,再根据位似变换的性质计算即可.
【解答】解:∵△OCD与△OAB位似,位似中心是原点O,点B的坐标为(﹣1.5,0),点D的坐标为(4.5,0),
∴△OCD与△OAB的相似比为3:1,
∵点A的坐标为(﹣2,﹣1),
∴点C的坐标为(﹣2×(﹣3),﹣1×(﹣3)),即(6,3),
故答案为:(6,3).
【点评】本题考查的是位似变换,正确求出相似比是解题的关键.
8.在方格图中,以格点为顶点的三角形叫做格点三角形.在如图所示的平面直角坐标系中,格点△ABC和△DEF成位似关系,则位似中心的坐标为 (﹣1,0) .
【考点】位似变换;坐标与图形性质.
【专题】图形的相似;推理能力.
【答案】(﹣1,0).
【分析】利用待定系数法求出直线AD的解析式,根据位似中心的概念解答即可.
【解答】解:设直线AD的解析式为y=kx+b,
∵点A的坐标为(1,2),点D的坐标为(3,4),
∴,
解得:,
∴直线AD的解析式为y=x+1,
由位似图形的概念可知:△ABC与△DEF的位似中心是直线AD与直线BE的交点,
∵直线y=x+1与x轴的交点是(﹣1,0),
∴位似中心的坐标为(﹣1,0).
【点评】本题考查的是位似图形的概念、待定系数法求一次函数解析式,掌握位似中心的概念是解题的关键.
9.如图,△ABO的顶点坐标是A(2,6),B(3,1),O(0,0),以点O为位似中心,将△ABO缩小为原来的,得到△A′B′O,则点A′的坐标为 (,2)或(,﹣2) .
【考点】位似变换;坐标与图形性质.
【专题】图形的相似;运算能力.
【答案】(,2)或(,﹣2).
【分析】根据位似变换的性质计算,得到答案.
【解答】解:∵以原点O为位似中心,把△ABC缩小为原来的,可以得到△A'B'O,点A的坐标为(2,6),
∴点A'的坐标是(2,6)或(2×(),6×()),即(,2)或(,﹣2).
故答案为:(,2)或(,﹣2).
【点评】本题考查的是位似变换的性质,在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或﹣k.
10.如图,△ABC和△DEF是以点O为位似中心的位似图形,相似比为2:3,则△ABC和△DEF的面积比是 4:9 .
【考点】位似变换.
【专题】图形的相似;运算能力.
【答案】4:9.
【分析】先利用位似的性质得到△ABC∽△DEF,相似比为2:3,然后根据相似三角形的性质解决问题.
【解答】解:∵△ABC与△DEF是以点O为位似中心的位似图形,位似比为2:3,
∴△ABC∽△DEF,相似比为2:3,
∴△ABC与△DEF的面积之比为22:32=4:9.
故答案为:4:9.
【点评】本题考查的是位似变换的概念和性质、相似三角形的性质,熟记相似三角形的面积比等于相似比的平方是解题的关键.
三.解答题(共5小题)
11.如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣2,1),B(﹣1,4),C(﹣3,2).
(1)画出△ABC关于y轴对称的图形△A1B1C1,并直接写出C1点的坐标;
(2)以原点O为位似中心,位似比为1:2,在y轴的左侧,画出△ABC放大后的图形△A2B2C2,并直接写出C2点坐标;
【考点】作图﹣位似变换;作图﹣轴对称变换.
【专题】平移、旋转与对称;图形的相似;几何直观.
【答案】(1)△A1B1C1见解答,(3,2);
(2)△A2B2C2见解答,(﹣6,4).
【分析】(1)分别作出三个顶点关于y轴的对称点,再首尾顺次连接即可;
(2)根据位似图形的概念作出三个顶点的对应点,再首尾顺次连接即可.
【解答】解:(1)如图所示,△A1B1C1即为所求,
由图知,C1点的坐标为(3,2);
(2)如图所示,△A2B2C2即为所求,C2点坐标为(﹣6,4).
【点评】本题主要考查作图—轴对称变换与位似变换,解题的关键是掌握轴对称变换与位似变换的定义与性质,并据此得出变换后的对应点.
12.如图所示,在平面直角坐标系中,△ABC的顶点坐标分别是A(1,0),B(3,1),C(2,3).请在所给直角坐标系中按要求画图和解答下列问题:
(1)画出△ABC关于x轴成轴对称的△A1B1C1,并直接写出点B1的坐标;
(2)以原点O为位似中心,在原点的另一侧画出△ABC的位似三角形△A2B2C2,使它与△ABC的相似比为2:1,并写出点C2的坐标.
【考点】作图﹣位似变换;作图﹣轴对称变换.
【专题】平移、旋转与对称;图形的相似;几何直观.
【答案】(1)画图见解答;B1(3,﹣1).
(2)画图见解答;C2(﹣4,﹣6).
【分析】(1)根据轴对称的性质作图,即可得出答案.
(2)根据位似的性质作图,即可得出答案.
【解答】解:(1)如图,△A1B1C1即为所求.
点B1的坐标为(3,﹣1).
(2)如图,△A2B2C2即为所求.
点C2的坐标为(﹣4,﹣6).
【点评】本题考查作图﹣轴对称变换、位似变换,熟练掌握轴对称的性质、位似的性质是解答本题的关键.
13.如图,△ABC在平面直角坐标系内三个顶点的坐标分别为A(﹣1,2),B(﹣3,3),C(﹣3,1).
(1)以点B为位似中心,在点B的下方画出△A1B1C1,使△A1B1C1与△ABC位似且相似比为3:1;
(2)点A1的坐标为 (3,0) ,点C1的坐标为 (﹣3,﹣3) .
【考点】作图﹣位似变换;点的坐标.
【专题】作图题;图形的相似;几何直观.
【答案】(1)见解析;
(2)(3,0),(﹣3,﹣3).
【分析】(1)在网格中作出A1、C1,连接A1C1、BC1、BA1即可得到△A1B1C1;
(2)根据点的位置写出A1、A1、C1的坐标即可.
【解答】解:(1)△A1B1C1即为所作;
(2)点A1的坐标为(3,0),点C1的坐标为(﹣3,﹣3),
故答案为:(3,0),(﹣3,﹣3).
【点评】本题考查了位似作图,图形与坐标,掌握位似的性质是解题的关键.
14.如图,在平面直角坐标系中,△ABC的顶点都在网格的格点上,按要求解决下列问题.
(1)画出△ABC关于y轴的轴对称图形△A1B1C1;
(2)以点O为位似中心,在第一象限中出画出△A2B2C2,使得△A1B1C1与△A2B2C2位似,且相似比为1:3.
【考点】作图﹣位似变换;作图﹣轴对称变换.
【专题】平移、旋转与对称;图形的相似;几何直观;推理能力.
【答案】(1)作图见解析过程;
(2)作图见解析过程.
【分析】(1)分别得出点A、B、C关于y轴的对称点,然后连线即可;
(2)由(1)及位似的性质进行作图即可.
【解答】解:(1)如图1所示,△A1B1C1即为所求.
(2)如图2所示,△A2B2C2即为所求.
【点评】本题主要考查轴对称及位似,熟练掌握轴对称及位似的性质是解题的关键.
15.如图,在平面直角坐标系中,给出了格点△ABC(顶点均在正方形网格的格点上),已知点A的坐标为(2,3).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)以点O为位似中心,在给定的网格中画出△A2B2C2,使△A2B2C2与△A1B1C1位似,并且点A2的坐标为(4,﹣6);
(3)△A1B1C1与△A2B2C2的相似比是 1:2 .
【考点】作图﹣位似变换;作图﹣轴对称变换.
【专题】作图题;平移、旋转与对称;几何直观.
【答案】(1)见解析;
(2)见解析;
(3)1:2.
【分析】(1)根据轴对称的性质作出图形即可;
(2)利用点A和A2的坐标特征得到位似比,再把B、C的横纵坐标都乘以2得到B2、C2的坐标,然后描点即可;
(3)根据相似三角形的性质即可得到结论.
【解答】解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求;
(3)∵△A1B1C1∽△A2B2C2,C1B1=3,C2B2=6
∴△A1B1C1与△A2B2C2的相似比1:2,
故答案为:1:2.
【点评】此题主要考查了作图﹣位似变换以及关于y轴对称点的性质,正确得出对应点位置是解题关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
