29.1投影(巩固复习.培优卷.含解析)-2024-2025学年人教版(2024)数学九年级下册
文档属性
| 名称 | 29.1投影(巩固复习.培优卷.含解析)-2024-2025学年人教版(2024)数学九年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 785.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-21 16:05:54 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
巩固复习.培优卷 投影
一.选择题(共5小题)
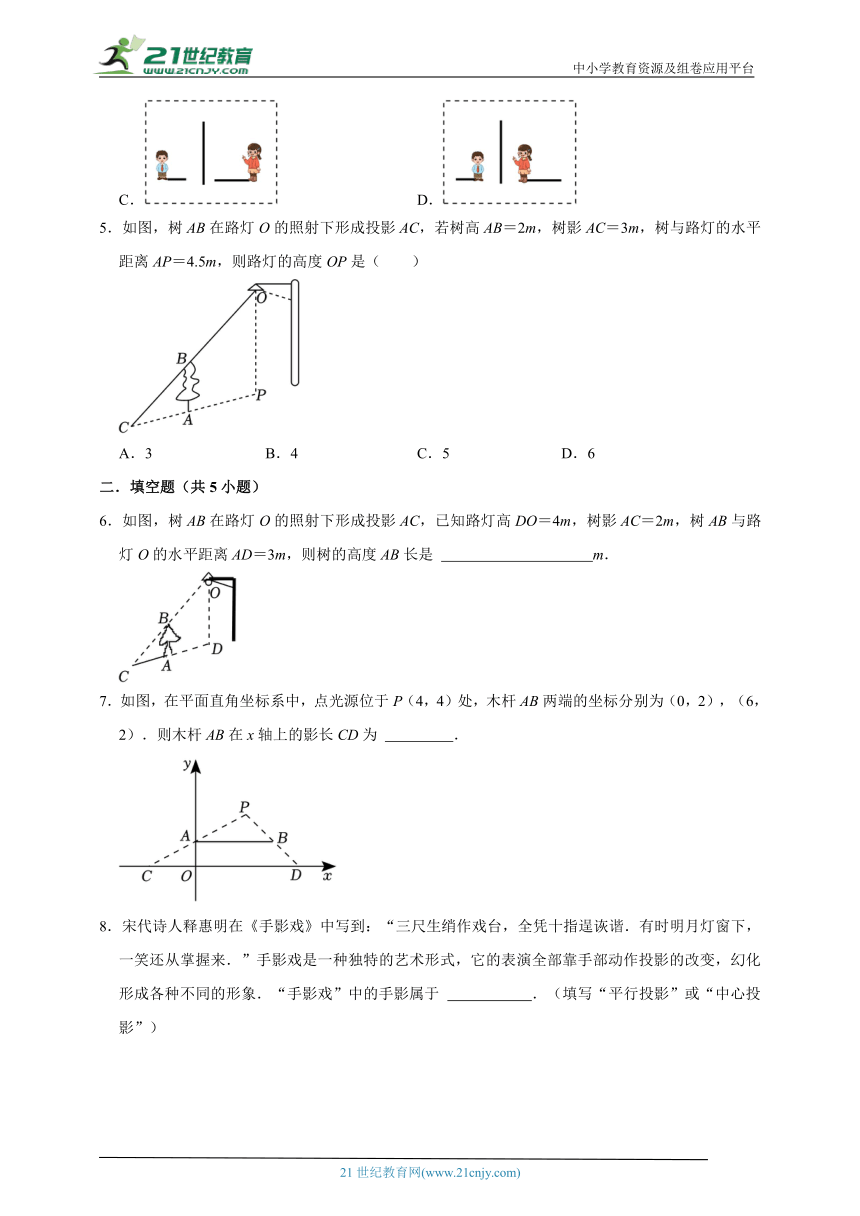
1.平地上立有三根等高的木杆,其俯视图如图所示,在某一时刻三根木杆在阳光下的影子可能是( )
A. B.
C. D.
2.如图,晚上小亮在路灯下散步,在小亮由A处走到B处这一过程中,他在地上的影子( )
A.逐渐变短 B.逐渐变长
C.先变短后变长 D.先变长后变短
3.小明拿一个等边三角形木框在阳光下玩,等边三角形木框在地上的投影不可能是( )
A.线段 B.一个点
C.等边三角形 D.等腰三角形
4.下列是描述小明和小颖在同一盏路灯下影子的图片,其中合理的是( )
A. B.
C. D.
5.如图,树AB在路灯O的照射下形成投影AC,若树高AB=2m,树影AC=3m,树与路灯的水平距离AP=4.5m,则路灯的高度OP是( )
A.3 B.4 C.5 D.6
二.填空题(共5小题)
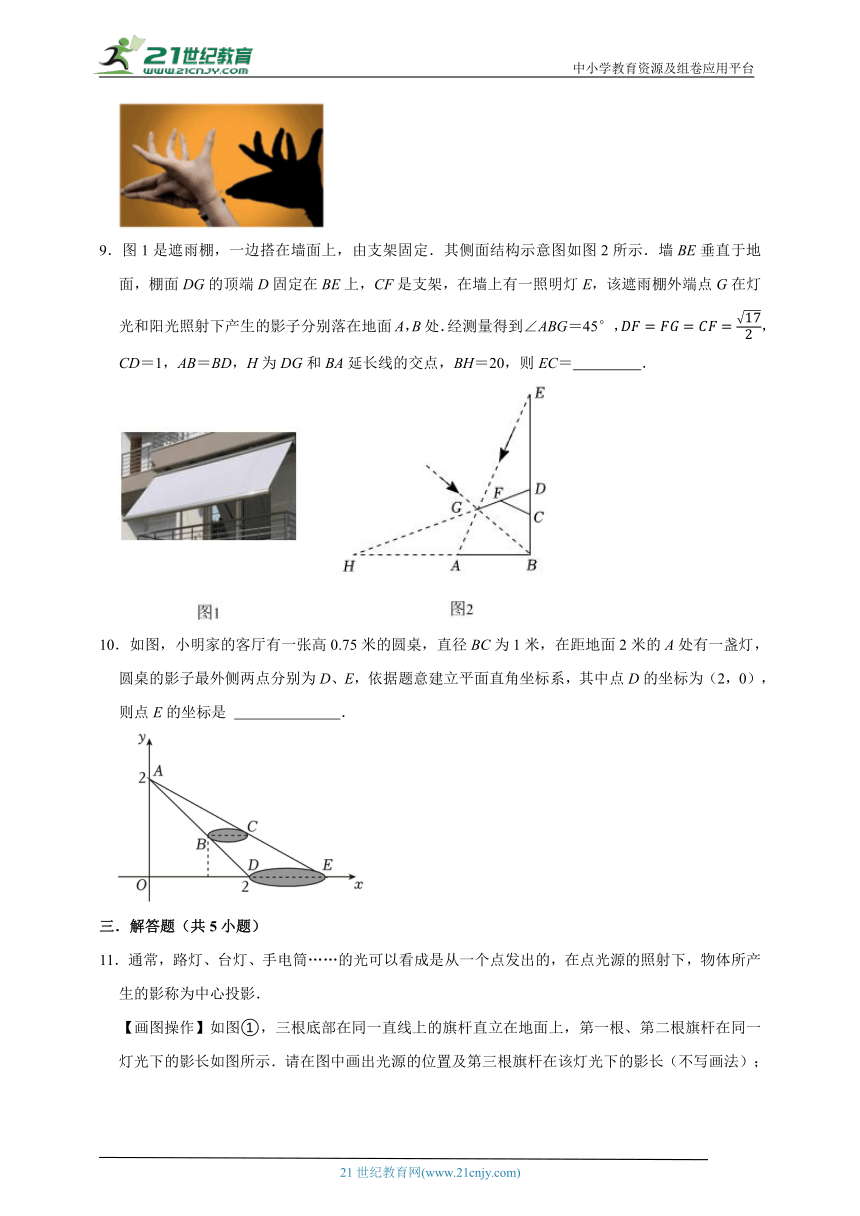
6.如图,树AB在路灯O的照射下形成投影AC,已知路灯高DO=4m,树影AC=2m,树AB与路灯O的水平距离AD=3m,则树的高度AB长是 m.
7.如图,在平面直角坐标系中,点光源位于P(4,4)处,木杆AB两端的坐标分别为(0,2),(6,2).则木杆AB在x轴上的影长CD为 .
8.宋代诗人释惠明在《手影戏》中写到:“三尺生绡作戏台,全凭十指逞诙谐.有时明月灯窗下,一笑还从掌握来.”手影戏是一种独特的艺术形式,它的表演全部靠手部动作投影的改变,幻化形成各种不同的形象.“手影戏”中的手影属于 .(填写“平行投影”或“中心投影”)
9.图1是遮雨棚,一边搭在墙面上,由支架固定.其侧面结构示意图如图2所示.墙BE垂直于地面,棚面DG的顶端D固定在BE上,CF是支架,在墙上有一照明灯E,该遮雨棚外端点G在灯光和阳光照射下产生的影子分别落在地面A,B处.经测量得到∠ABG=45°,,CD=1,AB=BD,H为DG和BA延长线的交点,BH=20,则EC= .
10.如图,小明家的客厅有一张高0.75米的圆桌,直径BC为1米,在距地面2米的A处有一盏灯,圆桌的影子最外侧两点分别为D、E,依据题意建立平面直角坐标系,其中点D的坐标为(2,0),则点E的坐标是 .
三.解答题(共5小题)
11.通常,路灯、台灯、手电筒……的光可以看成是从一个点发出的,在点光源的照射下,物体所产生的影称为中心投影.
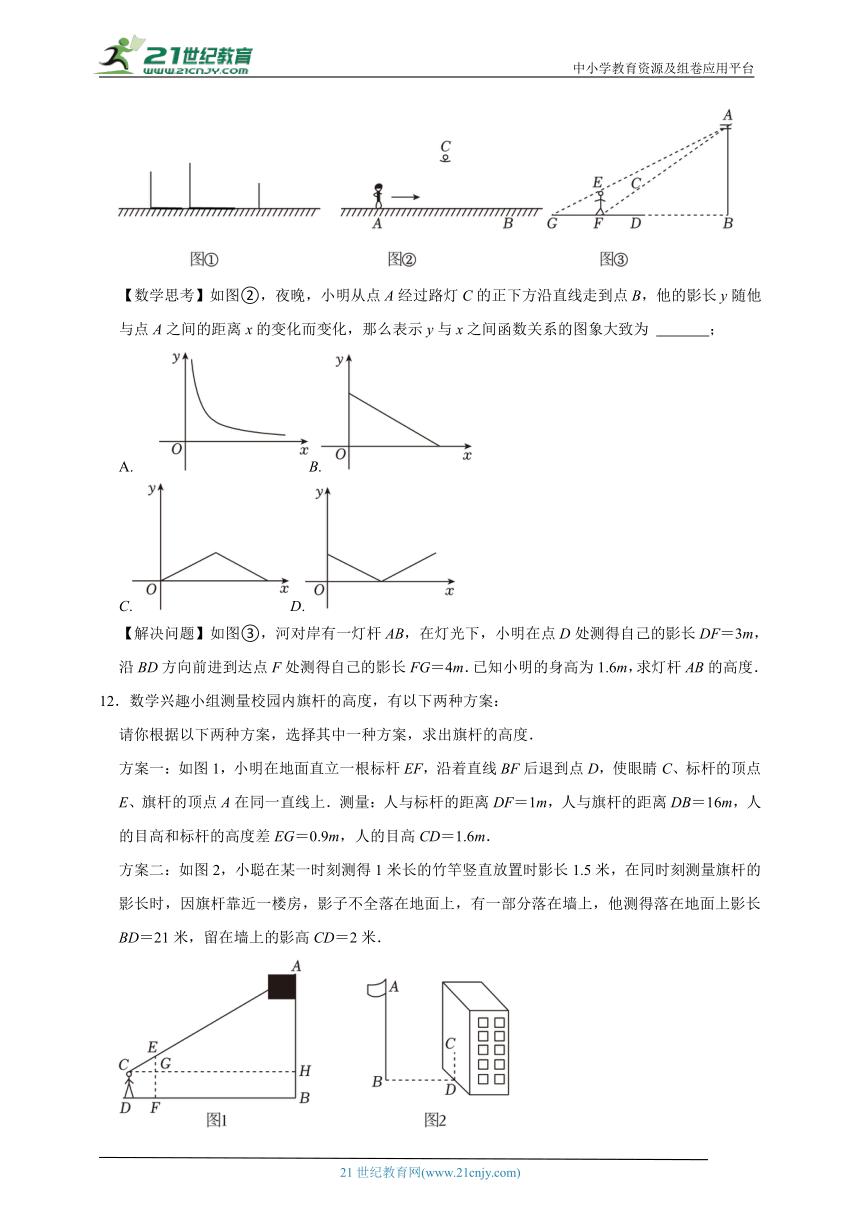
【画图操作】如图①,三根底部在同一直线上的旗杆直立在地面上,第一根、第二根旗杆在同一灯光下的影长如图所示.请在图中画出光源的位置及第三根旗杆在该灯光下的影长(不写画法);
【数学思考】如图②,夜晚,小明从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图象大致为 ;
B.
C.D.
【解决问题】如图③,河对岸有一灯杆AB,在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向前进到达点F处测得自己的影长FG=4m.已知小明的身高为1.6m,求灯杆AB的高度.
12.数学兴趣小组测量校园内旗杆的高度,有以下两种方案:
请你根据以下两种方案,选择其中一种方案,求出旗杆的高度.
方案一:如图1,小明在地面直立一根标杆EF,沿着直线BF后退到点D,使眼睛C、标杆的顶点E、旗杆的顶点A在同一直线上.测量:人与标杆的距离DF=1m,人与旗杆的距离DB=16m,人的目高和标杆的高度差EG=0.9m,人的目高CD=1.6m.
方案二:如图2,小聪在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长BD=21米,留在墙上的影高CD=2米.
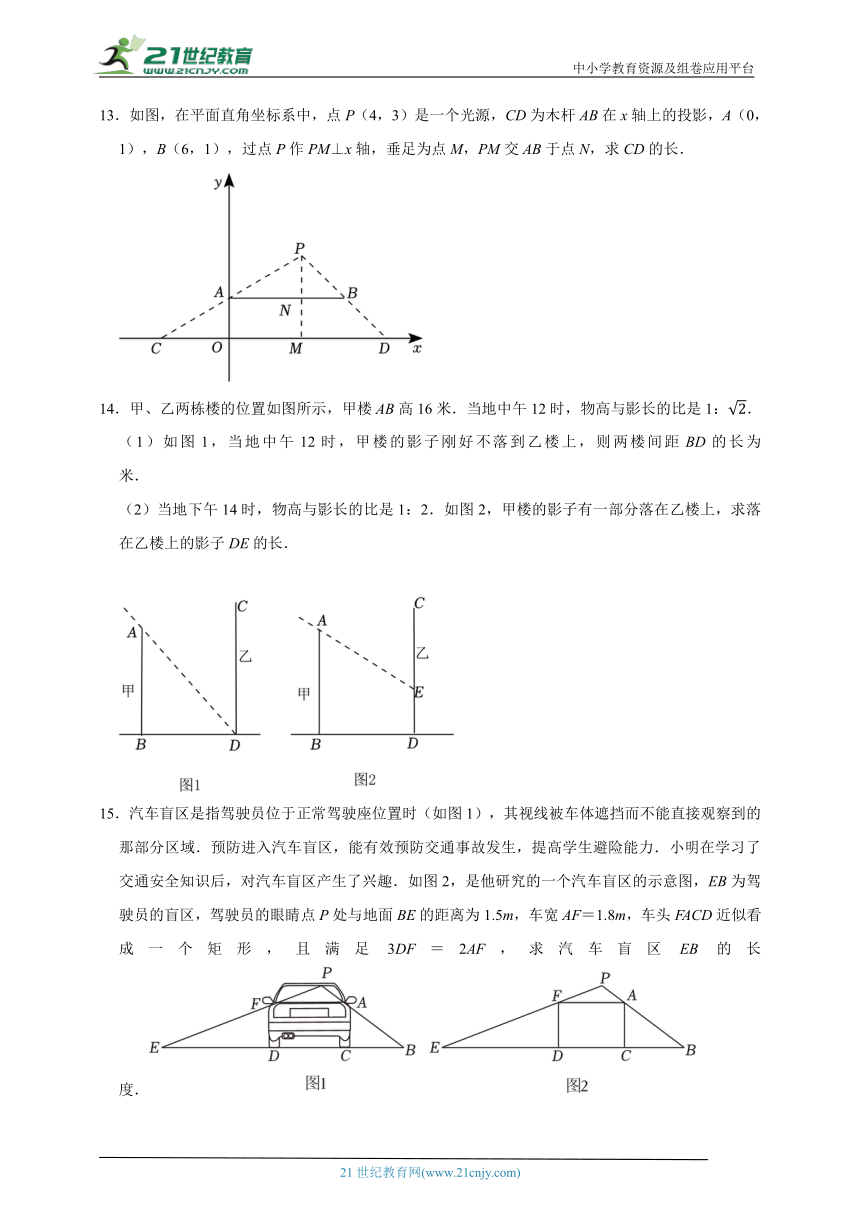
13.如图,在平面直角坐标系中,点P(4,3)是一个光源,CD为木杆AB在x轴上的投影,A(0,1),B(6,1),过点P作PM⊥x轴,垂足为点M,PM交AB于点N,求CD的长.
14.甲、乙两栋楼的位置如图所示,甲楼AB高16米.当地中午12时,物高与影长的比是1:.
(1)如图1,当地中午12时,甲楼的影子刚好不落到乙楼上,则两楼间距BD的长为 米.
(2)当地下午14时,物高与影长的比是1:2.如图2,甲楼的影子有一部分落在乙楼上,求落在乙楼上的影子DE的长.
15.汽车盲区是指驾驶员位于正常驾驶座位置时(如图1),其视线被车体遮挡而不能直接观察到的那部分区域.预防进入汽车盲区,能有效预防交通事故发生,提高学生避险能力.小明在学习了交通安全知识后,对汽车盲区产生了兴趣.如图2,是他研究的一个汽车盲区的示意图,EB为驾驶员的盲区,驾驶员的眼睛点P处与地面BE的距离为1.5m,车宽AF=1.8m,车头FACD近似看成一个矩形,且满足3DF=2AF,求汽车盲区EB的长度.
巩固复习.培优卷 投影
参考答案与试题解析
一.选择题(共5小题)
1.平地上立有三根等高的木杆,其俯视图如图所示,在某一时刻三根木杆在阳光下的影子可能是( )
A. B.
C. D.
【考点】平行投影.
【专题】投影与视图;几何直观.
【答案】D
【分析】根据平行投影的定义判断即可.
【解答】解:根据平行投影的定义可知,在某一时刻三根木杆在阳光下的影子可能是:
故选:D.
【点评】本题考查平行投影,解题的关键是理解平行投影的定义,属于中考常考题型.
2.如图,晚上小亮在路灯下散步,在小亮由A处走到B处这一过程中,他在地上的影子( )
A.逐渐变短 B.逐渐变长
C.先变短后变长 D.先变长后变短
【考点】中心投影.
【专题】投影与视图;推理能力.
【答案】C
【分析】根据中心投影的特点:等高的物体垂直地面放置时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.进行判断即可.
【解答】解:因为由A到B,离灯光由远到近再到远,所以影子先变短后变长.
故选:C.
【点评】本题综合考查了中心投影的特点和规律.中心投影的特点是:
①等高的物体垂直地面放置时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长;
②等长的物体平行于地面放置时,在灯光下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
3.小明拿一个等边三角形木框在阳光下玩,等边三角形木框在地上的投影不可能是( )
A.线段 B.一个点
C.等边三角形 D.等腰三角形
【考点】平行投影;等腰三角形的性质;等边三角形的性质.
【专题】投影与视图;几何直观.
【答案】B
【分析】在不同时刻,同一物体的影子的方向和大小可能不同,不同时刻物体在太阳光下的影子的大小在变,方向也在改变,依此进行分析.
【解答】解:当等边三角形木框与阳光平行时,投影是线段;
当等边三角形木框与阳光垂直时,投影是等边三角形;
当等边三角形木框与阳光有一定角度时,投影是等腰三角形;
投影不可能是一个点.
故选:B.
【点评】本题考查了平行投影特点,不同位置,不同时间,影子的大小、形状可能不同.
4.下列是描述小明和小颖在同一盏路灯下影子的图片,其中合理的是( )
A. B.
C. D.
【考点】中心投影.
【专题】投影与视图;几何直观.
【答案】D
【分析】利用“在同一时刻同一地点阳光下的影子的方向应该一致,人与影子的比相等”对各选项进行判断.
【解答】解:小明和小颖在同一盏路灯下影子与身高比例相等且影子方向相反.
故选:D.
【点评】本题考查中心投影的特点是:
①等高的物体垂直地面放置时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.
②等长的物体平行于地面放置时,在灯光下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
5.如图,树AB在路灯O的照射下形成投影AC,若树高AB=2m,树影AC=3m,树与路灯的水平距离AP=4.5m,则路灯的高度OP是( )
A.3 B.4 C.5 D.6
【考点】中心投影.
【专题】图形的相似;投影与视图;运算能力.
【答案】C
【分析】证明△ACB∽△PCO,利用相似三角形的性质求解即可.
【解答】解:∵AB∥OP,
∴△ACB∽△PCO,
∴,
∴,
∴OP=5(m),
故选:C.
【点评】本题考查中心投影,相似三角形的判定和性质,解题的关键是掌握中心投影的性质,属于中考常考题型.
二.填空题(共5小题)
6.如图,树AB在路灯O的照射下形成投影AC,已知路灯高DO=4m,树影AC=2m,树AB与路灯O的水平距离AD=3m,则树的高度AB长是 m.
【考点】中心投影.
【专题】图形的相似;运算能力;推理能力.
【答案】.
【分析】利用相似三角形的性质求解即可.
【解答】解:∵AB∥OD,
∴△CAB∽△CDO,
∴,
∴
∴AB(m),
答:树的高度AB长是m,
故答案为:.
【点评】本题考查中心投影以及相似三角形的应用.测量不能到达顶部的物体的高度,通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.
7.如图,在平面直角坐标系中,点光源位于P(4,4)处,木杆AB两端的坐标分别为(0,2),(6,2).则木杆AB在x轴上的影长CD为 12 .
【考点】中心投影;坐标确定位置.
【专题】投影与视图;推理能力.
【答案】见试题解答内容
【分析】利用中心投影,作PE⊥x轴于E,交AB于M,如图,证明△PAB∽△CPD,然后利用相似比可求出CD的长.
【解答】解:过P作PE⊥x轴于E,交AB于M,如图,
∵P(4,4),A(0,2),B(6,2).
∴PM=2,PE=4,AB=6,
∵AB∥CD,
∴.
∴,
∴CD=12,
故答案为:12.
【点评】本题考查了中心投影:中心投影的光线特点是从一点出发的投射线.物体与投影面平行时的投影是放大(即位似变换)的关系.
8.宋代诗人释惠明在《手影戏》中写到:“三尺生绡作戏台,全凭十指逞诙谐.有时明月灯窗下,一笑还从掌握来.”手影戏是一种独特的艺术形式,它的表演全部靠手部动作投影的改变,幻化形成各种不同的形象.“手影戏”中的手影属于 中心投影 .(填写“平行投影”或“中心投影”)
【考点】中心投影;平行投影.
【专题】投影与视图;推理能力.
【答案】中心投影.
【分析】根据中心投影和平行投影的定义即可判断.
【解答】解:由图可知,“手影戏”中的投影是光由一点向外散射形成的投影,属于中心投影,
故答案为:中心投影.
【点评】本题考查中心投影和平行投影的识别,解题的关键是掌握两者的定义:中心投影是指把光由一点向外散射形成的投影,平行投影是在一束平行光线照射下形成的投影.
9.图1是遮雨棚,一边搭在墙面上,由支架固定.其侧面结构示意图如图2所示.墙BE垂直于地面,棚面DG的顶端D固定在BE上,CF是支架,在墙上有一照明灯E,该遮雨棚外端点G在灯光和阳光照射下产生的影子分别落在地面A,B处.经测量得到∠ABG=45°,,CD=1,AB=BD,H为DG和BA延长线的交点,BH=20,则EC= 16 .
【考点】中心投影;平行投影.
【专题】解直角三角形及其应用;投影与视图;运算能力.
【答案】16.
【分析】连接CG,证明GC∥AB,推出,求出CG,AB,可得结论.
【解答】解:如图,连接CG.
∵BE⊥AB,∠ABG=45°,
∴∠EBG=90°﹣45°=45°,
∵FD=FC=FG,
∴∠GCD=90°,
∴∠CGB=∠CBG=45°,
∴CG=CB4,
∴AB=BD=BC+CD=4+1=5,
∵∠ECG=∠ABE=90°,
∴CG∥AB,
∴,
∴,
∴EC=16.
故答案为:16.
【点评】本题考查中心投影,平行投影,解题的关键是理解题意,灵活运用所学知识解决问题.
10.如图,小明家的客厅有一张高0.75米的圆桌,直径BC为1米,在距地面2米的A处有一盏灯,圆桌的影子最外侧两点分别为D、E,依据题意建立平面直角坐标系,其中点D的坐标为(2,0),则点E的坐标是 (3.6,0) .
【考点】中心投影;坐标确定位置.
【专题】图形的相似;投影与视图;推理能力.
【答案】(3.6,0).
【分析】根据相似三角形的相似比等于等于高的比,列方程求出DE,进而求出OE,确定点E的坐标.
【解答】解:过点B作BF⊥x轴,垂足为F,由题意得,BF=0.75米,BC=1米,
∵BC∥DE,
∴△ABC∽△ADE,
∴,
即:,
解得:DE=1.6(米),
∴OE=2+1.6=3.6(米),
∴E(3.6,0),
故答案为:(3.6,0).
【点评】本题考查的是中心投影,熟知将中心投影的问题转化为相似三角形的问题进行解答是解题的关键.
三.解答题(共5小题)
11.通常,路灯、台灯、手电筒……的光可以看成是从一个点发出的,在点光源的照射下,物体所产生的影称为中心投影.
【画图操作】如图①,三根底部在同一直线上的旗杆直立在地面上,第一根、第二根旗杆在同一灯光下的影长如图所示.请在图中画出光源的位置及第三根旗杆在该灯光下的影长(不写画法);
【数学思考】如图②,夜晚,小明从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图象大致为 D ;
A.
B.
C.
D.
【解决问题】如图③,河对岸有一灯杆AB,在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向前进到达点F处测得自己的影长FG=4m.已知小明的身高为1.6m,求灯杆AB的高度.
【考点】中心投影;函数的图象.
【专题】投影与视图;应用意识.
【答案】见试题解答内容
【分析】【画图操作】根据中心投影,直接画图即可;
【数学思考】等高的物体垂直地面时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长;
【解决问题】根据相似三角形的性质即可解答.
【解答】解:【画图操作】光源的位置及第三根旗杆在该灯光下的影长如图①所示;
【数学思考】如图②所示,等高的物体垂直地面时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长,所以小明的影长从A到B的变化是先越来越短再越来越长;
故答案为:D;
【解决问题】∵CD∥EF∥AB,
∴△CDF∽△ABF,△ABG∽△EFG,
∴,,
又∵CD=EF,
∴,
∵DF=3m,FG=4m,BF=BD+DF=(BD+3)(m),BG=BD+DF+FG=(BD+7)(m),
∴,
∴BD=9m,BF=9+3=12m,
∴,
解得:AB=6.4m;
∴灯杆AB的高度为6.4m.
【点评】本题考查了中心投影,相似三角形的性质的应用等,把实际问题抽象到相似三角形中,利用相似三角形的性质对应边成比例就可以求出结果.
12.数学兴趣小组测量校园内旗杆的高度,有以下两种方案:
请你根据以下两种方案,选择其中一种方案,求出旗杆的高度.
方案一:如图1,小明在地面直立一根标杆EF,沿着直线BF后退到点D,使眼睛C、标杆的顶点E、旗杆的顶点A在同一直线上.测量:人与标杆的距离DF=1m,人与旗杆的距离DB=16m,人的目高和标杆的高度差EG=0.9m,人的目高CD=1.6m.
方案二:如图2,小聪在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长BD=21米,留在墙上的影高CD=2米.
【考点】平行投影.
【答案】见解析,旗杆的高度是16米.
【分析】方案一:由题意得出CD∥EF∥AB,证出△ECG∽△ACH,得出对应边成比例,求出AH,即可得出结果;
方案二:延长AC,BD相交于点E,则CD:DE=1:1.5,得DE=1.5CD=3米,由CD∥AB,得出△ABE∽△CDE,得出对应边成比例,即可得出结果.
【解答】解:方案一:如图1所示:
由已知得:CD∥EF∥AB,
∴△ECG∽△ACH,
∴,即,
解得:AH=14.4米,
∴AB=AH+BH=14.4+1.6=16(米);
答:旗杆的高度是16米;
方案二:如图所示,延长AC,BD相交于点E,
则CD:DE=1:1.5,得DE=1.5CD=3米,
由已知CD∥AB,
∴△ABE∽△CDE,
∴,即,
解得:AB=16.
答:旗杆的高度是16米.
【点评】本题考查了相似三角形的应用、相似三角形的判定与性质;由题意证出三角形相似得出对应边成比例是解决问题的关键.
13.如图,在平面直角坐标系中,点P(4,3)是一个光源,CD为木杆AB在x轴上的投影,A(0,1),B(6,1),过点P作PM⊥x轴,垂足为点M,PM交AB于点N,求CD的长.
【考点】中心投影;坐标与图形性质;相似三角形的性质.
【专题】投影与视图;空间观念.
【答案】9.
【分析】根据坐标得出AB=6,AB∥x轴,PM、PN的值,根据相似三角形的性质得出答案.
【解答】解:∵A(0,1),B(6,1).
∴AB∥x轴,AB=6,
∵点P(4,3),
∴PM=3,PN=PM﹣MN=3﹣1=2,
∴△PAB∽△PCD,
∴,
即,
∴CD=9,
即CD的长为9.
【点评】本题考查中心投影,理解中心投影的意义,掌握相似三角形的性质是正确解答的关键.
14.甲、乙两栋楼的位置如图所示,甲楼AB高16米.当地中午12时,物高与影长的比是1:.
(1)如图1,当地中午12时,甲楼的影子刚好不落到乙楼上,则两楼间距BD的长为 米.
(2)当地下午14时,物高与影长的比是1:2.如图2,甲楼的影子有一部分落在乙楼上,求落在乙楼上的影子DE的长.
【考点】平行投影.
【专题】投影与视图;应用意识.
【答案】见试题解答内容
【分析】(1)根据物高与影长的比是1:列出比例式解答即可;
(2)设FE⊥AB于点F,那么在Rt△AEF中,∠AFE=90°,解直角三角形AEC可以求得AF的长,进而求得DE=AB﹣AF即可解题.
【解答】解:(1)由题意得:
,
即,
解得BD(米),
故答案为:;
(2)如图,
设FE⊥AB于点F,那么在Rt△AEF中,∠AFE=90°,EF=BD米.
∵物高与影长的比是1:2,
∴,
则AFEF(米),
故DE=FB=(16)米.
答:落在乙楼上的影子DE的长为(16)米.
【点评】本题考查了平行投影,根据物高与影长的比得出相关比例式是解题的关键.
15.汽车盲区是指驾驶员位于正常驾驶座位置时(如图1),其视线被车体遮挡而不能直接观察到的那部分区域.预防进入汽车盲区,能有效预防交通事故发生,提高学生避险能力.小明在学习了交通安全知识后,对汽车盲区产生了兴趣.如图2,是他研究的一个汽车盲区的示意图,EB为驾驶员的盲区,驾驶员的眼睛点P处与地面BE的距离为1.5m,车宽AF=1.8m,车头FACD近似看成一个矩形,且满足3DF=2AF,求汽车盲区EB的长度.
【考点】视点、视角和盲区;矩形的性质;相似三角形的判定与性质.
【专题】矩形 菱形 正方形;图形的相似;运算能力.
【答案】9m.
【分析】如图,过点P作PN⊥EB于点N,交AF于点M.理由相似三角形的性质求解.
【解答】解:如图,过点P作PN⊥EB于点N,交AF于点M.
∵3DF=2AF,AF=1.8m,
∴DF=1.2(m),
∵四边形ACDF是矩形,
∴∠FDC=90°,AF∥CD,
∴DF⊥DC,
∵MN⊥DC,
∴DF=MN=1.2(m),
∵PM=1.5m,
∴PM=PN﹣MN=1.5﹣1.2=0.3(m),
∵AF∥EB,
∴△PAF∽△PBE,
∴,
∴,
∴EB=9(m).
【点评】本题考查视点、视角和盲区,相似三角形的判定和性质,矩形的性质等知识,解题的关键是学会添加常用辅助线,理由相似三角形的性质解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
巩固复习.培优卷 投影
一.选择题(共5小题)
1.平地上立有三根等高的木杆,其俯视图如图所示,在某一时刻三根木杆在阳光下的影子可能是( )
A. B.
C. D.
2.如图,晚上小亮在路灯下散步,在小亮由A处走到B处这一过程中,他在地上的影子( )
A.逐渐变短 B.逐渐变长
C.先变短后变长 D.先变长后变短
3.小明拿一个等边三角形木框在阳光下玩,等边三角形木框在地上的投影不可能是( )
A.线段 B.一个点
C.等边三角形 D.等腰三角形
4.下列是描述小明和小颖在同一盏路灯下影子的图片,其中合理的是( )
A. B.
C. D.
5.如图,树AB在路灯O的照射下形成投影AC,若树高AB=2m,树影AC=3m,树与路灯的水平距离AP=4.5m,则路灯的高度OP是( )
A.3 B.4 C.5 D.6
二.填空题(共5小题)
6.如图,树AB在路灯O的照射下形成投影AC,已知路灯高DO=4m,树影AC=2m,树AB与路灯O的水平距离AD=3m,则树的高度AB长是 m.
7.如图,在平面直角坐标系中,点光源位于P(4,4)处,木杆AB两端的坐标分别为(0,2),(6,2).则木杆AB在x轴上的影长CD为 .
8.宋代诗人释惠明在《手影戏》中写到:“三尺生绡作戏台,全凭十指逞诙谐.有时明月灯窗下,一笑还从掌握来.”手影戏是一种独特的艺术形式,它的表演全部靠手部动作投影的改变,幻化形成各种不同的形象.“手影戏”中的手影属于 .(填写“平行投影”或“中心投影”)
9.图1是遮雨棚,一边搭在墙面上,由支架固定.其侧面结构示意图如图2所示.墙BE垂直于地面,棚面DG的顶端D固定在BE上,CF是支架,在墙上有一照明灯E,该遮雨棚外端点G在灯光和阳光照射下产生的影子分别落在地面A,B处.经测量得到∠ABG=45°,,CD=1,AB=BD,H为DG和BA延长线的交点,BH=20,则EC= .
10.如图,小明家的客厅有一张高0.75米的圆桌,直径BC为1米,在距地面2米的A处有一盏灯,圆桌的影子最外侧两点分别为D、E,依据题意建立平面直角坐标系,其中点D的坐标为(2,0),则点E的坐标是 .
三.解答题(共5小题)
11.通常,路灯、台灯、手电筒……的光可以看成是从一个点发出的,在点光源的照射下,物体所产生的影称为中心投影.
【画图操作】如图①,三根底部在同一直线上的旗杆直立在地面上,第一根、第二根旗杆在同一灯光下的影长如图所示.请在图中画出光源的位置及第三根旗杆在该灯光下的影长(不写画法);
【数学思考】如图②,夜晚,小明从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图象大致为 ;
B.
C.D.
【解决问题】如图③,河对岸有一灯杆AB,在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向前进到达点F处测得自己的影长FG=4m.已知小明的身高为1.6m,求灯杆AB的高度.
12.数学兴趣小组测量校园内旗杆的高度,有以下两种方案:
请你根据以下两种方案,选择其中一种方案,求出旗杆的高度.
方案一:如图1,小明在地面直立一根标杆EF,沿着直线BF后退到点D,使眼睛C、标杆的顶点E、旗杆的顶点A在同一直线上.测量:人与标杆的距离DF=1m,人与旗杆的距离DB=16m,人的目高和标杆的高度差EG=0.9m,人的目高CD=1.6m.
方案二:如图2,小聪在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长BD=21米,留在墙上的影高CD=2米.
13.如图,在平面直角坐标系中,点P(4,3)是一个光源,CD为木杆AB在x轴上的投影,A(0,1),B(6,1),过点P作PM⊥x轴,垂足为点M,PM交AB于点N,求CD的长.
14.甲、乙两栋楼的位置如图所示,甲楼AB高16米.当地中午12时,物高与影长的比是1:.
(1)如图1,当地中午12时,甲楼的影子刚好不落到乙楼上,则两楼间距BD的长为 米.
(2)当地下午14时,物高与影长的比是1:2.如图2,甲楼的影子有一部分落在乙楼上,求落在乙楼上的影子DE的长.
15.汽车盲区是指驾驶员位于正常驾驶座位置时(如图1),其视线被车体遮挡而不能直接观察到的那部分区域.预防进入汽车盲区,能有效预防交通事故发生,提高学生避险能力.小明在学习了交通安全知识后,对汽车盲区产生了兴趣.如图2,是他研究的一个汽车盲区的示意图,EB为驾驶员的盲区,驾驶员的眼睛点P处与地面BE的距离为1.5m,车宽AF=1.8m,车头FACD近似看成一个矩形,且满足3DF=2AF,求汽车盲区EB的长度.
巩固复习.培优卷 投影
参考答案与试题解析
一.选择题(共5小题)
1.平地上立有三根等高的木杆,其俯视图如图所示,在某一时刻三根木杆在阳光下的影子可能是( )
A. B.
C. D.
【考点】平行投影.
【专题】投影与视图;几何直观.
【答案】D
【分析】根据平行投影的定义判断即可.
【解答】解:根据平行投影的定义可知,在某一时刻三根木杆在阳光下的影子可能是:
故选:D.
【点评】本题考查平行投影,解题的关键是理解平行投影的定义,属于中考常考题型.
2.如图,晚上小亮在路灯下散步,在小亮由A处走到B处这一过程中,他在地上的影子( )
A.逐渐变短 B.逐渐变长
C.先变短后变长 D.先变长后变短
【考点】中心投影.
【专题】投影与视图;推理能力.
【答案】C
【分析】根据中心投影的特点:等高的物体垂直地面放置时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.进行判断即可.
【解答】解:因为由A到B,离灯光由远到近再到远,所以影子先变短后变长.
故选:C.
【点评】本题综合考查了中心投影的特点和规律.中心投影的特点是:
①等高的物体垂直地面放置时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长;
②等长的物体平行于地面放置时,在灯光下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
3.小明拿一个等边三角形木框在阳光下玩,等边三角形木框在地上的投影不可能是( )
A.线段 B.一个点
C.等边三角形 D.等腰三角形
【考点】平行投影;等腰三角形的性质;等边三角形的性质.
【专题】投影与视图;几何直观.
【答案】B
【分析】在不同时刻,同一物体的影子的方向和大小可能不同,不同时刻物体在太阳光下的影子的大小在变,方向也在改变,依此进行分析.
【解答】解:当等边三角形木框与阳光平行时,投影是线段;
当等边三角形木框与阳光垂直时,投影是等边三角形;
当等边三角形木框与阳光有一定角度时,投影是等腰三角形;
投影不可能是一个点.
故选:B.
【点评】本题考查了平行投影特点,不同位置,不同时间,影子的大小、形状可能不同.
4.下列是描述小明和小颖在同一盏路灯下影子的图片,其中合理的是( )
A. B.
C. D.
【考点】中心投影.
【专题】投影与视图;几何直观.
【答案】D
【分析】利用“在同一时刻同一地点阳光下的影子的方向应该一致,人与影子的比相等”对各选项进行判断.
【解答】解:小明和小颖在同一盏路灯下影子与身高比例相等且影子方向相反.
故选:D.
【点评】本题考查中心投影的特点是:
①等高的物体垂直地面放置时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长.
②等长的物体平行于地面放置时,在灯光下,离点光源越近,影子越长;离点光源越远,影子越短,但不会比物体本身的长度还短.
5.如图,树AB在路灯O的照射下形成投影AC,若树高AB=2m,树影AC=3m,树与路灯的水平距离AP=4.5m,则路灯的高度OP是( )
A.3 B.4 C.5 D.6
【考点】中心投影.
【专题】图形的相似;投影与视图;运算能力.
【答案】C
【分析】证明△ACB∽△PCO,利用相似三角形的性质求解即可.
【解答】解:∵AB∥OP,
∴△ACB∽△PCO,
∴,
∴,
∴OP=5(m),
故选:C.
【点评】本题考查中心投影,相似三角形的判定和性质,解题的关键是掌握中心投影的性质,属于中考常考题型.
二.填空题(共5小题)
6.如图,树AB在路灯O的照射下形成投影AC,已知路灯高DO=4m,树影AC=2m,树AB与路灯O的水平距离AD=3m,则树的高度AB长是 m.
【考点】中心投影.
【专题】图形的相似;运算能力;推理能力.
【答案】.
【分析】利用相似三角形的性质求解即可.
【解答】解:∵AB∥OD,
∴△CAB∽△CDO,
∴,
∴
∴AB(m),
答:树的高度AB长是m,
故答案为:.
【点评】本题考查中心投影以及相似三角形的应用.测量不能到达顶部的物体的高度,通常利用相似三角形的性质即相似三角形的对应边的比相等和“在同一时刻物高与影长的比相等”的原理解决.
7.如图,在平面直角坐标系中,点光源位于P(4,4)处,木杆AB两端的坐标分别为(0,2),(6,2).则木杆AB在x轴上的影长CD为 12 .
【考点】中心投影;坐标确定位置.
【专题】投影与视图;推理能力.
【答案】见试题解答内容
【分析】利用中心投影,作PE⊥x轴于E,交AB于M,如图,证明△PAB∽△CPD,然后利用相似比可求出CD的长.
【解答】解:过P作PE⊥x轴于E,交AB于M,如图,
∵P(4,4),A(0,2),B(6,2).
∴PM=2,PE=4,AB=6,
∵AB∥CD,
∴.
∴,
∴CD=12,
故答案为:12.
【点评】本题考查了中心投影:中心投影的光线特点是从一点出发的投射线.物体与投影面平行时的投影是放大(即位似变换)的关系.
8.宋代诗人释惠明在《手影戏》中写到:“三尺生绡作戏台,全凭十指逞诙谐.有时明月灯窗下,一笑还从掌握来.”手影戏是一种独特的艺术形式,它的表演全部靠手部动作投影的改变,幻化形成各种不同的形象.“手影戏”中的手影属于 中心投影 .(填写“平行投影”或“中心投影”)
【考点】中心投影;平行投影.
【专题】投影与视图;推理能力.
【答案】中心投影.
【分析】根据中心投影和平行投影的定义即可判断.
【解答】解:由图可知,“手影戏”中的投影是光由一点向外散射形成的投影,属于中心投影,
故答案为:中心投影.
【点评】本题考查中心投影和平行投影的识别,解题的关键是掌握两者的定义:中心投影是指把光由一点向外散射形成的投影,平行投影是在一束平行光线照射下形成的投影.
9.图1是遮雨棚,一边搭在墙面上,由支架固定.其侧面结构示意图如图2所示.墙BE垂直于地面,棚面DG的顶端D固定在BE上,CF是支架,在墙上有一照明灯E,该遮雨棚外端点G在灯光和阳光照射下产生的影子分别落在地面A,B处.经测量得到∠ABG=45°,,CD=1,AB=BD,H为DG和BA延长线的交点,BH=20,则EC= 16 .
【考点】中心投影;平行投影.
【专题】解直角三角形及其应用;投影与视图;运算能力.
【答案】16.
【分析】连接CG,证明GC∥AB,推出,求出CG,AB,可得结论.
【解答】解:如图,连接CG.
∵BE⊥AB,∠ABG=45°,
∴∠EBG=90°﹣45°=45°,
∵FD=FC=FG,
∴∠GCD=90°,
∴∠CGB=∠CBG=45°,
∴CG=CB4,
∴AB=BD=BC+CD=4+1=5,
∵∠ECG=∠ABE=90°,
∴CG∥AB,
∴,
∴,
∴EC=16.
故答案为:16.
【点评】本题考查中心投影,平行投影,解题的关键是理解题意,灵活运用所学知识解决问题.
10.如图,小明家的客厅有一张高0.75米的圆桌,直径BC为1米,在距地面2米的A处有一盏灯,圆桌的影子最外侧两点分别为D、E,依据题意建立平面直角坐标系,其中点D的坐标为(2,0),则点E的坐标是 (3.6,0) .
【考点】中心投影;坐标确定位置.
【专题】图形的相似;投影与视图;推理能力.
【答案】(3.6,0).
【分析】根据相似三角形的相似比等于等于高的比,列方程求出DE,进而求出OE,确定点E的坐标.
【解答】解:过点B作BF⊥x轴,垂足为F,由题意得,BF=0.75米,BC=1米,
∵BC∥DE,
∴△ABC∽△ADE,
∴,
即:,
解得:DE=1.6(米),
∴OE=2+1.6=3.6(米),
∴E(3.6,0),
故答案为:(3.6,0).
【点评】本题考查的是中心投影,熟知将中心投影的问题转化为相似三角形的问题进行解答是解题的关键.
三.解答题(共5小题)
11.通常,路灯、台灯、手电筒……的光可以看成是从一个点发出的,在点光源的照射下,物体所产生的影称为中心投影.
【画图操作】如图①,三根底部在同一直线上的旗杆直立在地面上,第一根、第二根旗杆在同一灯光下的影长如图所示.请在图中画出光源的位置及第三根旗杆在该灯光下的影长(不写画法);
【数学思考】如图②,夜晚,小明从点A经过路灯C的正下方沿直线走到点B,他的影长y随他与点A之间的距离x的变化而变化,那么表示y与x之间函数关系的图象大致为 D ;
A.
B.
C.
D.
【解决问题】如图③,河对岸有一灯杆AB,在灯光下,小明在点D处测得自己的影长DF=3m,沿BD方向前进到达点F处测得自己的影长FG=4m.已知小明的身高为1.6m,求灯杆AB的高度.
【考点】中心投影;函数的图象.
【专题】投影与视图;应用意识.
【答案】见试题解答内容
【分析】【画图操作】根据中心投影,直接画图即可;
【数学思考】等高的物体垂直地面时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长;
【解决问题】根据相似三角形的性质即可解答.
【解答】解:【画图操作】光源的位置及第三根旗杆在该灯光下的影长如图①所示;
【数学思考】如图②所示,等高的物体垂直地面时,在灯光下,离点光源近的物体它的影子短,离点光源远的物体它的影子长,所以小明的影长从A到B的变化是先越来越短再越来越长;
故答案为:D;
【解决问题】∵CD∥EF∥AB,
∴△CDF∽△ABF,△ABG∽△EFG,
∴,,
又∵CD=EF,
∴,
∵DF=3m,FG=4m,BF=BD+DF=(BD+3)(m),BG=BD+DF+FG=(BD+7)(m),
∴,
∴BD=9m,BF=9+3=12m,
∴,
解得:AB=6.4m;
∴灯杆AB的高度为6.4m.
【点评】本题考查了中心投影,相似三角形的性质的应用等,把实际问题抽象到相似三角形中,利用相似三角形的性质对应边成比例就可以求出结果.
12.数学兴趣小组测量校园内旗杆的高度,有以下两种方案:
请你根据以下两种方案,选择其中一种方案,求出旗杆的高度.
方案一:如图1,小明在地面直立一根标杆EF,沿着直线BF后退到点D,使眼睛C、标杆的顶点E、旗杆的顶点A在同一直线上.测量:人与标杆的距离DF=1m,人与旗杆的距离DB=16m,人的目高和标杆的高度差EG=0.9m,人的目高CD=1.6m.
方案二:如图2,小聪在某一时刻测得1米长的竹竿竖直放置时影长1.5米,在同时刻测量旗杆的影长时,因旗杆靠近一楼房,影子不全落在地面上,有一部分落在墙上,他测得落在地面上影长BD=21米,留在墙上的影高CD=2米.
【考点】平行投影.
【答案】见解析,旗杆的高度是16米.
【分析】方案一:由题意得出CD∥EF∥AB,证出△ECG∽△ACH,得出对应边成比例,求出AH,即可得出结果;
方案二:延长AC,BD相交于点E,则CD:DE=1:1.5,得DE=1.5CD=3米,由CD∥AB,得出△ABE∽△CDE,得出对应边成比例,即可得出结果.
【解答】解:方案一:如图1所示:
由已知得:CD∥EF∥AB,
∴△ECG∽△ACH,
∴,即,
解得:AH=14.4米,
∴AB=AH+BH=14.4+1.6=16(米);
答:旗杆的高度是16米;
方案二:如图所示,延长AC,BD相交于点E,
则CD:DE=1:1.5,得DE=1.5CD=3米,
由已知CD∥AB,
∴△ABE∽△CDE,
∴,即,
解得:AB=16.
答:旗杆的高度是16米.
【点评】本题考查了相似三角形的应用、相似三角形的判定与性质;由题意证出三角形相似得出对应边成比例是解决问题的关键.
13.如图,在平面直角坐标系中,点P(4,3)是一个光源,CD为木杆AB在x轴上的投影,A(0,1),B(6,1),过点P作PM⊥x轴,垂足为点M,PM交AB于点N,求CD的长.
【考点】中心投影;坐标与图形性质;相似三角形的性质.
【专题】投影与视图;空间观念.
【答案】9.
【分析】根据坐标得出AB=6,AB∥x轴,PM、PN的值,根据相似三角形的性质得出答案.
【解答】解:∵A(0,1),B(6,1).
∴AB∥x轴,AB=6,
∵点P(4,3),
∴PM=3,PN=PM﹣MN=3﹣1=2,
∴△PAB∽△PCD,
∴,
即,
∴CD=9,
即CD的长为9.
【点评】本题考查中心投影,理解中心投影的意义,掌握相似三角形的性质是正确解答的关键.
14.甲、乙两栋楼的位置如图所示,甲楼AB高16米.当地中午12时,物高与影长的比是1:.
(1)如图1,当地中午12时,甲楼的影子刚好不落到乙楼上,则两楼间距BD的长为 米.
(2)当地下午14时,物高与影长的比是1:2.如图2,甲楼的影子有一部分落在乙楼上,求落在乙楼上的影子DE的长.
【考点】平行投影.
【专题】投影与视图;应用意识.
【答案】见试题解答内容
【分析】(1)根据物高与影长的比是1:列出比例式解答即可;
(2)设FE⊥AB于点F,那么在Rt△AEF中,∠AFE=90°,解直角三角形AEC可以求得AF的长,进而求得DE=AB﹣AF即可解题.
【解答】解:(1)由题意得:
,
即,
解得BD(米),
故答案为:;
(2)如图,
设FE⊥AB于点F,那么在Rt△AEF中,∠AFE=90°,EF=BD米.
∵物高与影长的比是1:2,
∴,
则AFEF(米),
故DE=FB=(16)米.
答:落在乙楼上的影子DE的长为(16)米.
【点评】本题考查了平行投影,根据物高与影长的比得出相关比例式是解题的关键.
15.汽车盲区是指驾驶员位于正常驾驶座位置时(如图1),其视线被车体遮挡而不能直接观察到的那部分区域.预防进入汽车盲区,能有效预防交通事故发生,提高学生避险能力.小明在学习了交通安全知识后,对汽车盲区产生了兴趣.如图2,是他研究的一个汽车盲区的示意图,EB为驾驶员的盲区,驾驶员的眼睛点P处与地面BE的距离为1.5m,车宽AF=1.8m,车头FACD近似看成一个矩形,且满足3DF=2AF,求汽车盲区EB的长度.
【考点】视点、视角和盲区;矩形的性质;相似三角形的判定与性质.
【专题】矩形 菱形 正方形;图形的相似;运算能力.
【答案】9m.
【分析】如图,过点P作PN⊥EB于点N,交AF于点M.理由相似三角形的性质求解.
【解答】解:如图,过点P作PN⊥EB于点N,交AF于点M.
∵3DF=2AF,AF=1.8m,
∴DF=1.2(m),
∵四边形ACDF是矩形,
∴∠FDC=90°,AF∥CD,
∴DF⊥DC,
∵MN⊥DC,
∴DF=MN=1.2(m),
∵PM=1.5m,
∴PM=PN﹣MN=1.5﹣1.2=0.3(m),
∵AF∥EB,
∴△PAF∽△PBE,
∴,
∴,
∴EB=9(m).
【点评】本题考查视点、视角和盲区,相似三角形的判定和性质,矩形的性质等知识,解题的关键是学会添加常用辅助线,理由相似三角形的性质解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
