第二章 相交线与平行线(巩固复习.培优卷.含解析)-2024-2025学年北师大版(2024)数学七年级下册
文档属性
| 名称 | 第二章 相交线与平行线(巩固复习.培优卷.含解析)-2024-2025学年北师大版(2024)数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 515.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-21 16:04:41 | ||
图片预览
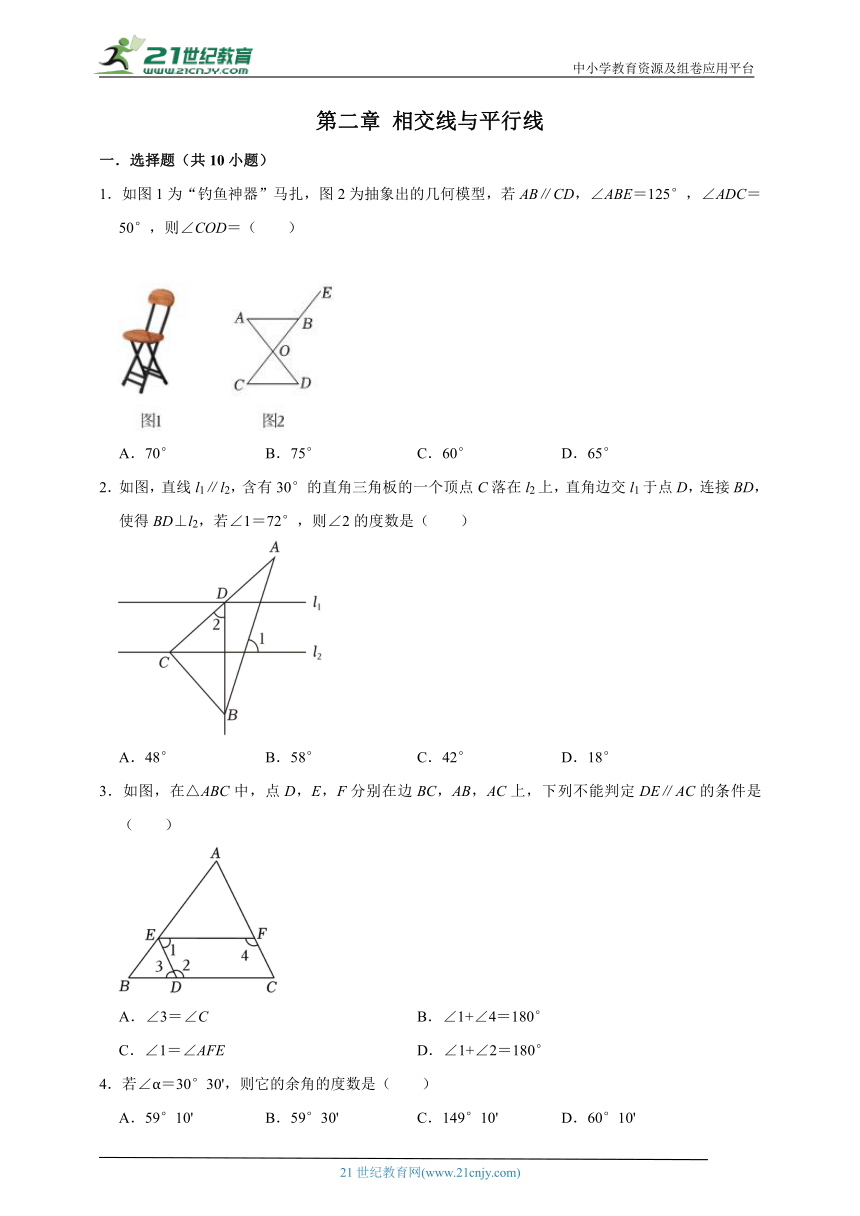
文档简介
中小学教育资源及组卷应用平台
第二章 相交线与平行线
一.选择题(共10小题)
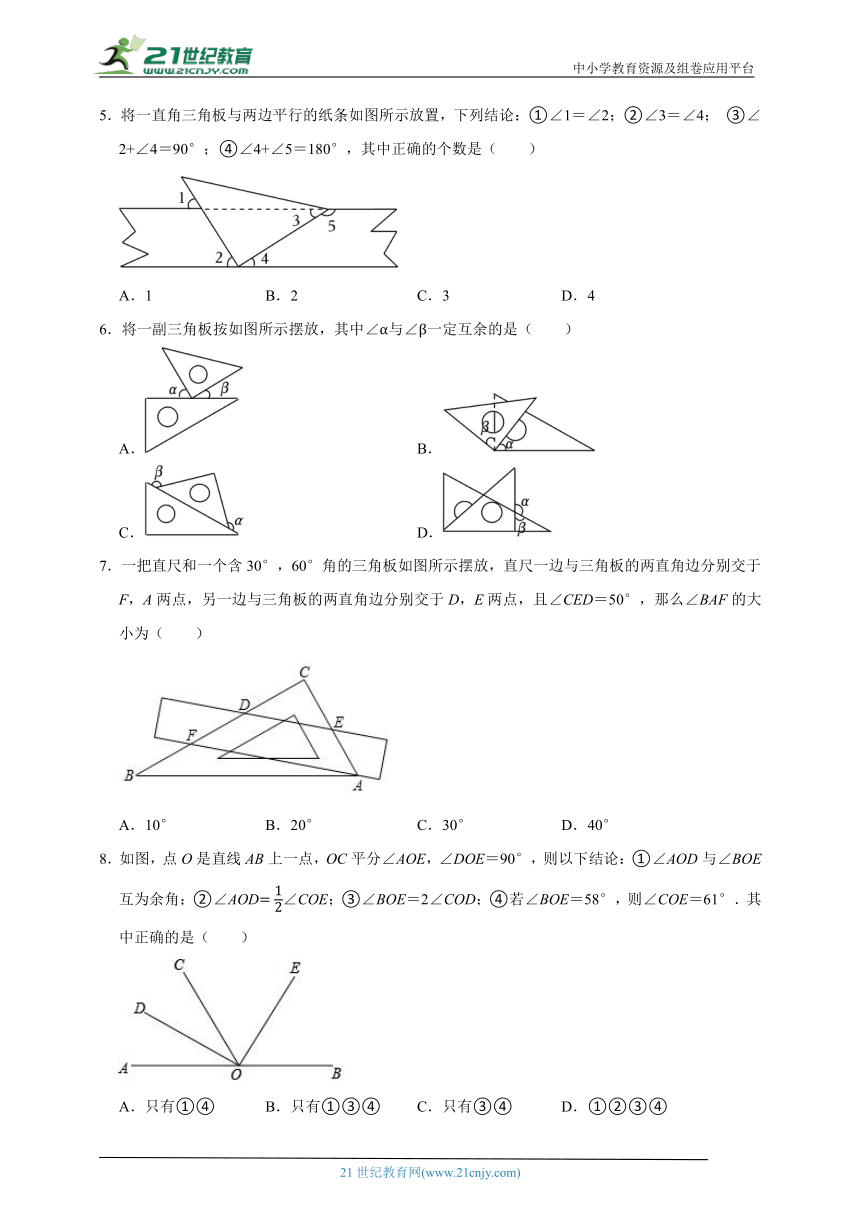
1.如图1为“钓鱼神器”马扎,图2为抽象出的几何模型,若AB∥CD,∠ABE=125°,∠ADC=50°,则∠COD=( )
A.70° B.75° C.60° D.65°
2.如图,直线l1∥l2,含有30°的直角三角板的一个顶点C落在l2上,直角边交l1于点D,连接BD,使得BD⊥l2,若∠1=72°,则∠2的度数是( )
A.48° B.58° C.42° D.18°
3.如图,在△ABC中,点D,E,F分别在边BC,AB,AC上,下列不能判定DE∥AC的条件是( )
A.∠3=∠C B.∠1+∠4=180°
C.∠1=∠AFE D.∠1+∠2=180°
4.若∠α=30°30',则它的余角的度数是( )
A.59°10' B.59°30' C.149°10' D.60°10'
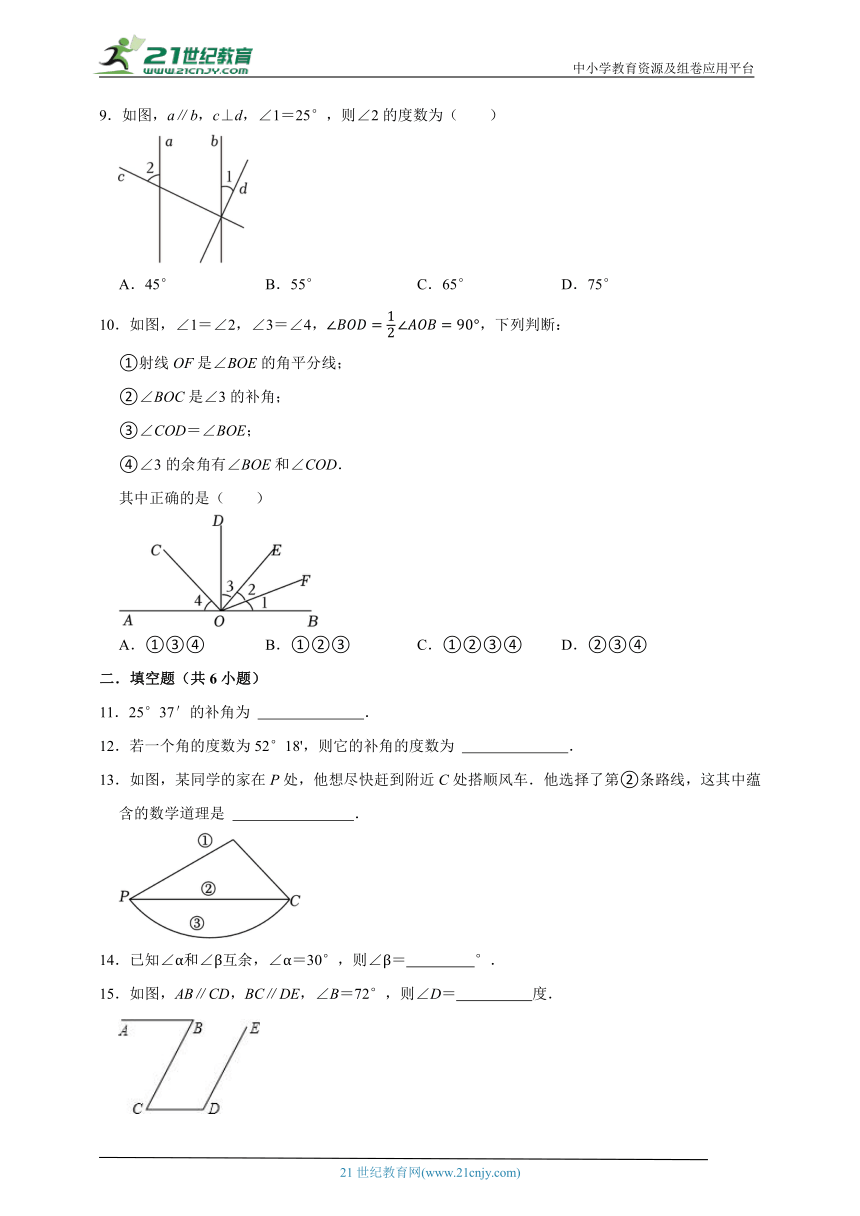
5.将一直角三角板与两边平行的纸条如图所示放置,下列结论:①∠1=∠2;②∠3=∠4; ③∠2+∠4=90°;④∠4+∠5=180°,其中正确的个数是( )
A.1 B.2 C.3 D.4
6.将一副三角板按如图所示摆放,其中∠α与∠β一定互余的是( )
A. B.
C. D.
7.一把直尺和一个含30°,60°角的三角板如图所示摆放,直尺一边与三角板的两直角边分别交于F,A两点,另一边与三角板的两直角边分别交于D,E两点,且∠CED=50°,那么∠BAF的大小为( )
A.10° B.20° C.30° D.40°
8.如图,点O是直线AB上一点,OC平分∠AOE,∠DOE=90°,则以下结论:①∠AOD与∠BOE互为余角;②∠AOD∠COE;③∠BOE=2∠COD;④若∠BOE=58°,则∠COE=61°.其中正确的是( )
A.只有①④ B.只有①③④ C.只有③④ D.①②③④
9.如图,a∥b,c⊥d,∠1=25°,则∠2的度数为( )
A.45° B.55° C.65° D.75°
10.如图,∠1=∠2,∠3=∠4,,下列判断:
①射线OF是∠BOE的角平分线;
②∠BOC是∠3的补角;
③∠COD=∠BOE;
④∠3的余角有∠BOE和∠COD.
其中正确的是( )
A.①③④ B.①②③ C.①②③④ D.②③④
二.填空题(共6小题)
11.25°37′的补角为 .
12.若一个角的度数为52°18',则它的补角的度数为 .
13.如图,某同学的家在P处,他想尽快赶到附近C处搭顺风车.他选择了第②条路线,这其中蕴含的数学道理是 .
14.已知∠α和∠β互余,∠α=30°,则∠β= °.
15.如图,AB∥CD,BC∥DE,∠B=72°,则∠D= 度.
16.已知一个角的余角比这个角的补角的一半还小12°,则这个角的度数为 .
三.解答题(共9小题)
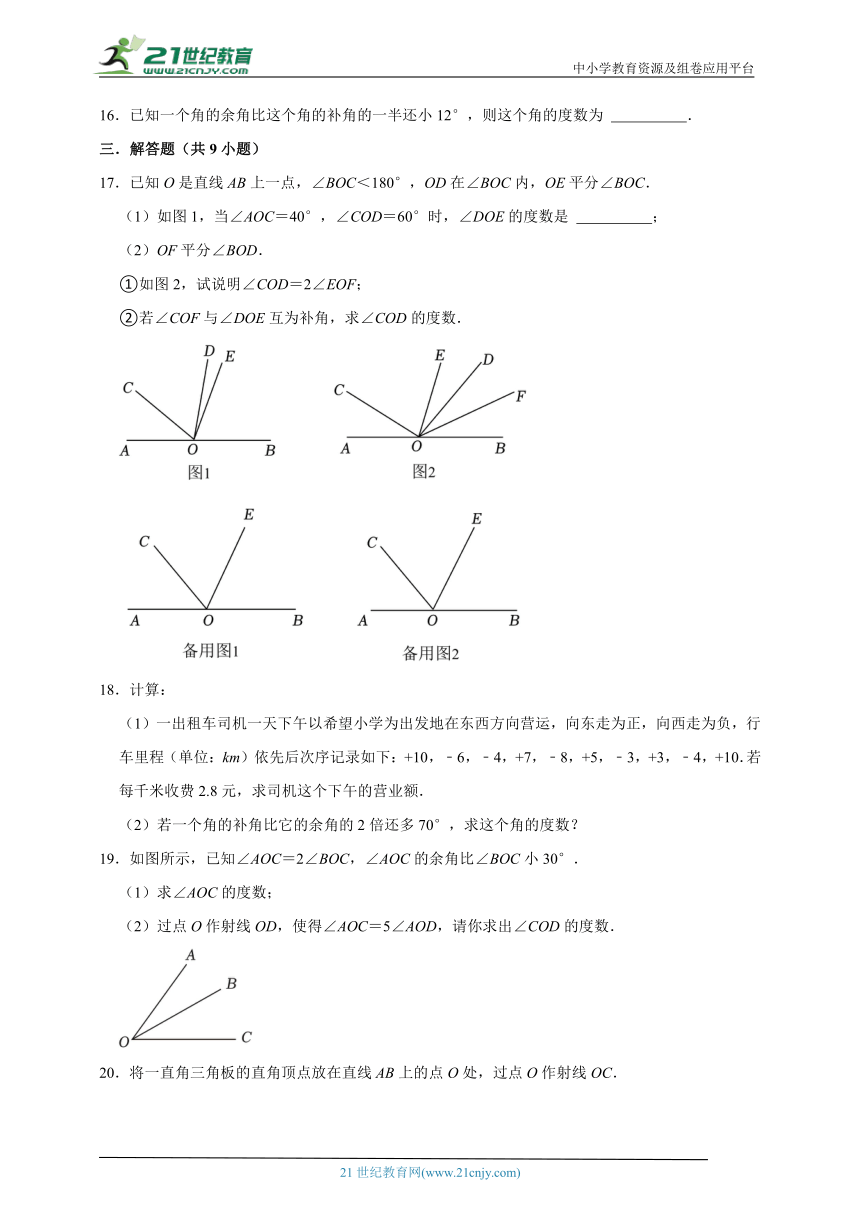
17.已知O是直线AB上一点,∠BOC<180°,OD在∠BOC内,OE平分∠BOC.
(1)如图1,当∠AOC=40°,∠COD=60°时,∠DOE的度数是 ;
(2)OF平分∠BOD.
①如图2,试说明∠COD=2∠EOF;
②若∠COF与∠DOE互为补角,求∠COD的度数.
18.计算:
(1)一出租车司机一天下午以希望小学为出发地在东西方向营运,向东走为正,向西走为负,行车里程(单位:km)依先后次序记录如下:+10,﹣6,﹣4,+7,﹣8,+5,﹣3,+3,﹣4,+10.若每千米收费2.8元,求司机这个下午的营业额.
(2)若一个角的补角比它的余角的2倍还多70°,求这个角的度数?
19.如图所示,已知∠AOC=2∠BOC,∠AOC的余角比∠BOC小30°.
(1)求∠AOC的度数;
(2)过点O作射线OD,使得∠AOC=5∠AOD,请你求出∠COD的度数.
20.将一直角三角板的直角顶点放在直线AB上的点O处,过点O作射线OC.
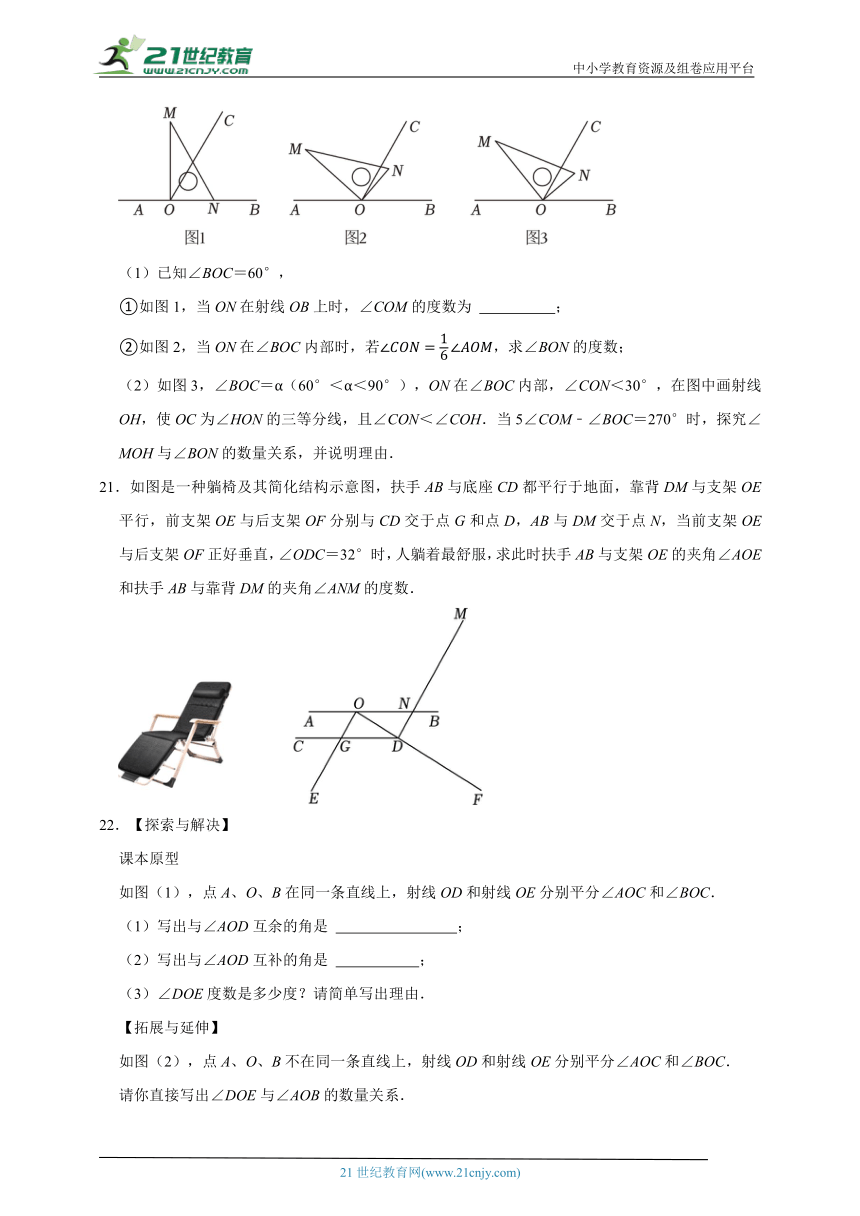
(1)已知∠BOC=60°,
①如图1,当ON在射线OB上时,∠COM的度数为 ;
②如图2,当ON在∠BOC内部时,若,求∠BON的度数;
(2)如图3,∠BOC=α(60°<α<90°),ON在∠BOC内部,∠CON<30°,在图中画射线OH,使OC为∠HON的三等分线,且∠CON<∠COH.当5∠COM﹣∠BOC=270°时,探究∠MOH与∠BON的数量关系,并说明理由.
21.如图是一种躺椅及其简化结构示意图,扶手AB与底座CD都平行于地面,靠背DM与支架OE平行,前支架OE与后支架OF分别与CD交于点G和点D,AB与DM交于点N,当前支架OE与后支架OF正好垂直,∠ODC=32°时,人躺着最舒服,求此时扶手AB与支架OE的夹角∠AOE和扶手AB与靠背DM的夹角∠ANM的度数.
22.【探索与解决】
课本原型
如图(1),点A、O、B在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)写出与∠AOD互余的角是 ;
(2)写出与∠AOD互补的角是 ;
(3)∠DOE度数是多少度?请简单写出理由.
【拓展与延伸】
如图(2),点A、O、B不在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC.
请你直接写出∠DOE与∠AOB的数量关系.
23.如图,已知∠AOB的补角等于它的余角的10倍.
(1)求∠AOB的度数;
(2)若OD平分∠BOC,∠AOC=3∠BOD,求∠AOD的度数.
24.(1)将一副直角三角板ABC,ADE按如图1所示位置摆放,∠BAC=45°,∠EAD=60°.分别作∠BAE,∠CAD的平分线AM,AN.试求∠MAN的度数;
(2)将三角板ADE从图1位置开始绕点A顺时针旋转到图2所示的位置,AM、AN仍然是∠BAE,∠CAD的平分线.试求∠MAN的度数;
(3)将三角板ADE从图1位置开始绕点A顺时针旋转α°(0°<α<360°),AM、AN仍然是∠BAE,∠CAD的平分线.在旋转的过程中,∠MAN的度数会发生改变吗?请说明理由.
25.综合与探究
问题情境:
数学活动课上,老师以直线AB上一点O为端点作射线OC,OD,OM,ON,使OM平分∠AOC,ON平分∠BOD,若∠COD=α,求∠MOC+∠DON的度数.
特例探究:
(1)从特殊到一般是研究几何的一般思路,如图2,“兴趣小组”将一个三角尺的直角顶点放在点O处,即当∠COD=90°时,则∠MOC+∠DON的度数为 ;(直接写出答案,不写过程)
(2)受“兴趣小组”的启发,“智慧小组”将三角尺60°角的顶点放在点O处,即当∠COD=60°时,请你在图3中求∠MOC+∠DON的度数;
数学思考:
(3)请你在图1中,求∠MOC+∠DON的度数(用含有α的式子表示).
第二章 相交线与平行线
参考答案与试题解析
一.选择题(共10小题)
1.【答案】B
【分析】根据两直线平行,内错角相等得出∠A的度数,再根据三角形外角的性质即可求出∠AOB的度数,最后根据对顶角的性质即可求出∠COD的度数.
【解答】解:∵AB∥CD,∠ADC=50°,
∴∠A=∠ADC=50°,
∵∠ABE是△AOB的外角,∠ABE=125°,
∴∠AOB=∠ABE﹣∠A=125°﹣50°=75°,
∴∠COD=∠AOB=75°,
故选:B.
【点评】本题考查了平行线的性质,三角形外角的性质,对顶角的性质,熟练掌握这些知识点是解题的关键.
2.【答案】A
【分析】根据平行的性质可得∠DEB=∠1=72°,根据三角形的外角的定义可得∠ADC=42°,再根据平角进行计算即可得到答案.
【解答】解:如图,设AB与l1相交于点E,
∵l1∥l2,∠1=72°,
∴∠DEB=∠1=72°,
∵∠A+∠ADC=∠DEB=72°,∠A=30°,
∴∠ADE=42°,
∵∠ADC+∠BDE+∠2=180°,BD⊥l2,
∴∠2=48°.
故选:A.
【点评】本题主要考查了平行线的性质、三角形外角的定义,平角的定义,熟练掌握平行线的性质、三角形外角的定义,平角的定义是解题的关键.
3.【答案】D
【分析】利用平行线的判定方法分别分析得出答案.
【解答】解:A、当∠C=∠3时,DE∥AC,故不符合题意;
B、当∠1+∠4=180°时,DE∥AC,故不符合题意;
C、当∠1=∠AFE时,DE∥AC,故不符合题意;
D、当∠1+∠2=180°时,EF∥BC,不能判定DE∥AC,故符合题意.
故选:D.
【点评】本题主要考查了平行线的判定,正确掌握平行线的判定方法是解题关键.
4.【答案】B
【分析】互余两角的和等于90°,90°与∠α的差,就是它的余角.
【解答】解:90°﹣∠α=90°﹣30°30′=59°30′.
故答案为:B.
【点评】本题考查了两角互为余角的定义,度分秒换算,关键是两角减法,1°=60′.
5.【答案】D
【分析】根据平行线的性质,直角三角板的性质对各小题进行验证即可得解.
【解答】解:∵纸条的两边互相平行,
∴∠1=∠2,∠3=∠4,∠4+∠5=180°,故①,②,④正确;
∵三角板是直角三角板,
∴∠2+∠4=180°﹣90°=90°,故③正确.
综上所述,正确的个数是4.
故选:D.
【点评】本题考查了平行线的性质,直角三角板的性质,熟记性质与概念并准确识图是解题的关键.
6.【答案】A
【分析】根据每个图形中∠α与∠β的关系进行判断,即可找出一定互余的图形.
【解答】解:A中的∠α与∠β的和等于平角减去一个直角,是90°,故A中的∠α与∠β一定互余;
B中的∠α与∠β是同一个角的余角,一定相等,但是不一定互余,故B排除;
C中∠α与∠β都是钝角,不可能互余,故C排除;
D中∠α与∠β互为邻补,不可能互余,故D排除.
故选:A.
【点评】本题主要考查余角,熟练掌握互为余角的定义是解决问题的关键.
7.【答案】A
【分析】先根据∠CED=50°,DE∥AF,即可得到∠CAF=50°,最后根据∠BAC=60°,即可得出∠BAF的大小.
【解答】解:∵DE∥AF,∠CED=50°,
∴∠CAF=∠CED=50°,
∵∠BAC=60°,
∴∠BAF=60°﹣50°=10°,
故选:A.
【点评】本题主要考查了平行线的性质以及直角三角形的性质的运用,解题解题的关键是掌握平行线的性质:两直线平行,同位角相等.
8.【答案】B
【分析】根据补角以及角平分线的定义解决此题.
【解答】解:①由∠DOE=90°,得∠AOD+∠BOE=180°﹣∠DOE=90°,那么∠AOD与∠BOE互为余角,故①正确.
②由OC平分∠AOE,得∠AOC=∠COE,无法推断得到∠AOD∠COE,故②错误.
③设∠COD=x,由∠DOE=90°,得∠COE=90°﹣x.由OC平分∠AOE,得∠AOC=∠COE,那么∠AOD=90°﹣2x,进而推断出∠BOE=2x,也就是说∠BOE=2∠COD,故③正确.
④由∠BOE=58°,得∠AOE=180°﹣∠BOE=122°.由OC平分∠AOE,得∠COE61°,故④正确.
综上:正确的有①③④.
故选:B.
【点评】本题主要考查角平分线、补角,熟练掌握角平分线的定义以及补角的定义是解决本题的关键.
9.【答案】C
【分析】先利用垂直性质求∠3度数,再利用平行线性质求∠2度数.
【解答】解:如图:
∵c⊥d,
∴∠1+∠3=90°,
∵∠1=25°,
∴∠3=65°,
∵a∥b,
∠2=∠3=65°.
故选:C.
【点评】本题考查了平行线的性质,掌握平行线的性质是解题关键.
10.【答案】C
【分析】根据角平分线的定义和互为余角、互为补角的定义判断即可.
【解答】解:①∵∠1=∠2,∴射线OF是∠BOE的角平分线,故正确;
②∵∠BOC+∠4=180°,又∵∠3=∠4,∴∠BOC+∠3=180°,即∠BOC是∠3的补角,故正确;
③∵,∴∠AOD=90°,∠BOE+∠3=90°,∴∠4+∠COD=90°,∵∠3=∠4,∴∠COD=∠BOE,故正确;
④∠3的余角有∠BOE和∠COD,故正确.
正确的是①②③④,
故选:C.
【点评】本题考查了余角和补角,角平分线的定义,正确识别图形是解题的关键.
二.填空题(共6小题)
11.【答案】154°23′.
【分析】根据互为补角的定义,列出算式,进行计算即可.
【解答】解:25°37′的补角为:
180°﹣25°37′
=179°60′﹣25°37′
=154°23′,
故答案为:154°23′.
【点评】本题主要考查了互为补角定义和度分秒的换算,解题关键是熟练掌握互为补角的两个角的和为180°.
12.【答案】127°42'.
【分析】如果两个角的和为180°,那么这两个角互为补角;由此计算即可.
【解答】解:若一个角的度数为52°18',
则它的补角的度数为180°﹣52°18'=179°60'﹣52°18'=127°42',
故答案为:127°42'.
【点评】本题考查了余角和补角,度分秒的换算,熟知互为补角的定义是解题的关键.
13.【答案】两点之间,线段最短.
【分析】根据两点之间,线段最短进行判断即可.
【解答】解:在点P与点C之间所有的连线中,线段最短,即两点之间,线段最短.
故答案为:两点之间,线段最短.
【点评】本题考查线段的性质,掌握两点之间,线段最短是正确判断的关键.
14.【答案】见试题解答内容
【分析】根据余角的定义计算.
【解答】解:已知∠α和∠β互余,∠α=30°,
则∠β=90°﹣∠α=60°.
故答案为:60.
【点评】本题考查余角的定义:如果两个角的和为90°,则这两个角互为余角.
15.【答案】见试题解答内容
【分析】先根据AB∥CD求出∠C的度数,再由BC∥DE即可求出∠D的度数.
【解答】解:∵AB∥CD,∠B=72°,
∴∠C=∠B=72°,
∵BC∥DE,
∴∠D=180°﹣∠C=180°﹣72°=108°.
故答案为:108.
【点评】本题考查的是平行线的性质,即两直线平行,内错角相等,同旁内角互补.
16.【答案】24°.
【分析】设这个角为x,则它的余角是90°﹣x,它的补角是180°﹣x,列方程求解即可.
【解答】解:设这个角为x,
则它的余角是90°﹣x,它的补角是180°﹣x,
由题意,得:90°﹣x+12°(180°﹣x),
解得:x=24°,
即这个角的度数是24°.
故答案为:24°.
【点评】本题考查了余角和补角,掌握互余的两角之和为90°,互补的两角之和为180°是解题的关键.
三.解答题(共9小题)
17.【答案】(1)10°;
(2)①证明见解析;
②120°.
【分析】(1)根据平角定义和已知条件,求出∠BOC,再根据角平分线的定义先求出∠COE的度数,再减去∠COD的度数即可;
(2)①先根据角平分线的定义证明∠COE=∠DOB,∠DOF=∠BOF,然后根据∠COD=∠COE+∠DOF,最后代换成2(∠DOE+∠DOF)进行解答即可;
②先根据已知条件得到∠COF+∠DOE=180°,从而得到∠COD+∠DOF+∠DOE=180°,根据①的结论,得到关于∠EOF的方程,求出∠EOF,再求出∠COD即可.
【解答】解:(1)∵O是直线AB上一点,
∴∠AOC+∠BOC=180°,
∵∠AOC=40°,
∴∠BOC=180°﹣40°=140°,
∵OE平分∠BOC,
∴∠COE,
∵∠COD=60°,
∴∠DOE=∠COE﹣∠COD=70°﹣60°=10°,
故答案为:10°;
(2)证明:①∵OE平分∠BOC,
∴∠COE=∠DOB,
∵OF平分∠BOD,
∴∠DOF=∠BOF,
∵∠COD=∠COE+∠DOE,
∴∠COD=∠BOE+∠DOE
=∠DOE+∠DOF+∠BOF+∠DOE,
=∠DOE+∠DOF+∠DOF+∠DOE
=2∠DOE+2∠DOF
=2(∠DOE+∠DOF)
=2∠EOF;
②∵∠COF与∠DOE互为补角,
∴∠COF+∠DOE=180°,
∴∠COD+∠DOF+∠DOE=180°,
∠COD+∠EOF=180°,
2∠EOF+∠EOF=180°,
3∠EOF=180°,
∴∠EOF=60°,
∴∠COD=2∠EOF=120°.
【点评】本题主要考查了角的有关运算,解题关键是正确识别图形,理解角与角之间的和差倍分关系.
18.【答案】(1)168元;
(2)70°.
【分析】(1)把每次行车里程相加求出这天下午的总里程,然后乘单价即可求出司机这个下午的营业额;
(2)设这个角为x,分别表示出其补角和余角,根据题意列出方程然后解方程即可求出这个角的度数.
【解答】解:(1)10+6+4+7+8+5+3+3+4+10=60(km),
2.8×60=168(元).
答:司机这个下午的营业额为168元.
(2)设这个角为x,则其补角度数为180°﹣x,余角度数为90°﹣x,
由题意得:180°﹣x=2(90°﹣x)+70,
解得:x=70°,
∴这个角的度数为70°.
【点评】本题主要考查正数和负数以及余角和补角,熟练掌握正负数的意义和求一个角余角、补角的方法是解决问题的关键.
19.【答案】(1)∠AOC=80°;
(2)64°或96°.
【分析】(1)设∠BOC=x,则∠AOC=2x,根据,∠AOC的余角比∠BOC小30°列方程求解即可;
(2)分两种情况:①当射线OD在∠AOC内部②当射线OD在∠AOC外部,分别求出∠COD的度数即可.
【解答】解:(1)设∠BOC=x,则∠AOC=2x,
依题意列方程90°﹣2x=x﹣30°,
解得:x=40°,
即∠AOC=40°×2=80°.
(2)由(1)得,∠AOC=80°,
①当射线OD在∠AOC内部时,∠AOD=16°,
则∠COD=∠AOC﹣∠AOD=80°﹣16°=64°;
②当射线OD在∠AOC外部时,∠AOD=16°,
则∠COD=∠AOC+∠AOD=80°+16°=96°.
【点评】本题考查了余角和补角的知识,解答本题的关键是掌握互余两角之和为90°,互补两角之和为180°.
20.【答案】(1)①30°;
②55°;
(2)∠BON=2∠HOM.理由见解析.
【分析】(1)①根据余角的定义即可得到结论;
②设∠CON=α,∠AOM=6α,求得∠BON=60°﹣α,列方程得到α=5°,于是得到∠BON=60°﹣5°=55°;
(2)根据OC为∠HON的三等分线,设∠CON=β,∠COH=2β,得到∠BON=α﹣β,∠COM=90°﹣β,列方程得到α=180°﹣5β,于是得到∠BON=2∠HOM.
【解答】解:(1)①∵∠BOM=90°,∠BOC=60°,
∴∠COM=90°﹣60°=30°;
故答案为:30°;
②∵,
∴设∠CON=α,∠AOM=6α,
∵∠BOC=60°,
∴∠BON=60°﹣α,
∴∠AOM=180°﹣90°﹣(60°﹣α)=6α,
∴α=5°,
∴∠BON=60°﹣5°=55°;
(2)∠BON=2∠HOM.
理由:如图,
∵OC为∠HON的三等分线,
∴设∠CON=β,∠COH=2β,
∵∠BOC=α,
∴∠BON=α﹣β,
∴∠COM=90°﹣β,
∵5∠COM﹣∠BOC=270°,
∴5(90°﹣β)﹣α=270°,
∴α=180°﹣5β,
∴∠BON=∠BOC﹣∠CON=180°﹣6β=2(90°﹣3β),
∵∠HOM=90°﹣∠COH﹣∠CON=90°﹣3β,
∴∠BON=2∠HOM.
【点评】本题考查了余角与补角,一元一次方程的应用,正确的识别图形是解题的关键.
21.【答案】122°.
【分析】先根据平行线的性质,得出∠ODC=∠BOD=32°,再根据∠EOF=90°,即可得到∠AOE=58°,再根据平行线的性质,即可得到∠AND的度数,进而得出∠ANM的度数.
【解答】解:∵扶手AB与底座CD都平行于地面,
∴AB∥CD,
∴∠ODC=∠BOD=32°,
又∵∠EOF=90°,
∴∠AOE=58°,
∵DM∥OE,
∴∠AND=∠AOE=58°,
∴∠ANM=180°﹣∠AND=122°.
【点评】本题主要考查了平行线的性质的运用,掌握两直线平行,内错角相等;两直线平行,同位角相等是解题的关键.
22.【答案】【探索与解决】(1)∠COE,∠BOE;
(2)∠BOD;
(3)∠DOE=90°;
理由见解析;
【拓展与延伸】∠COD∠AOB.
【分析】【探索与解决】(1)根据角平分线的定义得到∠COD=∠AOD∠AOC,∠COE=∠BOE∠BOC,于是得到∠AOD与∠COE互为余角,∠AOD与∠BOE互为余角;
(2)根据互为补角的定义即可得到结论;
(3)根据角平分线的定义和角的和差即可得到结论;
【拓展与延伸】根据角平分线的定义和角的和差即可得到结论.
【解答】解:【探索与解决】(1)∵点A,O,B在同一条直线上,
∵射线OD和射线OE分别平分∠AOC和∠BOC,
∴∠COD=∠AOD∠AOC,∠COE=∠BOE∠BOC,
∴∠COD+∠COE∠AOC∠BOC180°=90°.
∴∠AOD与∠COE互为余角,∠AOD与∠BOE互为余角;
故答案为:∠COE,∠BOE;
(2)∠AOD与∠BOD分别互为补角,
故答案为:∠BOD;
(3)∠DOE=90°;
理由:∵射线OD和射线OE分别平分∠AOC和∠BOC,
∴∠COD=∠AOD∠AOC,∠COE=∠BOE∠BOC,
∴∠COD+∠COE∠AOC∠BOC180°=90°,
∴∠DOE=90°;
【拓展与延伸】∵射线OD和射线OE分别平分∠AOC和∠BOC,
∴∠COD=∠AOD∠AOC,∠COE=∠BOE∠BOC,
∴∠COD+∠COE∠AOC∠BOCAOB.
【点评】本题主要考查补角与余角、角平分线,熟练掌握补角与余角、角平分线的定义是解决本题的关键.
23.【答案】(1)80°.
(2)160°.
【分析】(1)利用设元法列方程求解即可.
(2)设∠BOD=y,利用题目条件列出关于y的方程求解即可.
【解答】解:(1)设∠AOB=x,
由题意得:180°﹣x=10(90°﹣x),
解得x=80°.
所以∠AOB的度数为80°.
(2)设∠BOD=y,则∠AOC=3y,
∵OD平分∠BOC,
∴∠BOC=2∠BOD=2y,
由题意得:2y+80°=3y°,
解得y=80°,
∴∠AOD=∠AOB+∠BOD=80°+80°=160°.
【点评】本题考查角度的计算、补角和余角的概念,熟练掌握设元法求角的方法是解题关键.
24.【答案】(1)52.5°;(2)52.5°;(3)不变,理由见详解.
【分析】(1)根据题意求得∠MAE、∠NAE,再相加即可;
(2)用已知60°、45°、∠DAB来分别表示∠MAB、∠NAD,再减去∠DAB即可;
(3)通过画图考虑到∠BAE.∠CAD为钝角时的情况,根据(2)的思路解答即可.
【解答】解:(1)∵AM,AN是∠BAE,∠CAD的平分线,
∴∠MAE=22.5°,∠NAE=30°,
∴∠MAN=∠MAE+∠NAE=22.5°+30°=52.5°.
(2)∠MAB;,
∠MAN=∠MAB+∠NAD﹣∠BAD∠BAD=30°+22.5=52.5°;
(3)不变,在旋转过程中,∠BAE.∠CAD为钝角时,如图示:
∵∠MAE,,
∴∠MAN=∠MAE+∠NAC﹣∠CAE∠CAE=52.5°.
【点评】本题考查了角平分线的定义,熟练掌握角平分线的定义是解答本题的关键.
25.【答案】(1)45°;(2)60°;(3).
【分析】(1)求得∠AOC+∠BOD=90°,利用角平分线的定义得,据此求解即可;
(2)求得∠AOC+∠BOD=120°,利用角平分线的定义得,据此求解即可;
(3)求得∠AOC+∠BOD=180°﹣α,利用角平分线的定义得求解即可.
【解答】解:(1)因为∠COD=90°,所以∠AOC+∠BOD=90°,
因为OM平分∠AOC,ON平分∠BOD,
所以,,
所以
;
故答案为:45°;
(2)因为∠COD=60°,所以∠AOC+∠BOD=120°,
因为OM平分∠AOC,ON平分∠BOD,
所以,,
所以
;
(3)因为∠COD=α,所以∠AOC+∠BOD=180°﹣α,
因为OM平分∠AOC,ON平分∠BOD,
所以,,
所以
.
【点评】本题考查角度计算,涉及角平分线的定义,解题的关键是根据题意得到.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二章 相交线与平行线
一.选择题(共10小题)
1.如图1为“钓鱼神器”马扎,图2为抽象出的几何模型,若AB∥CD,∠ABE=125°,∠ADC=50°,则∠COD=( )
A.70° B.75° C.60° D.65°
2.如图,直线l1∥l2,含有30°的直角三角板的一个顶点C落在l2上,直角边交l1于点D,连接BD,使得BD⊥l2,若∠1=72°,则∠2的度数是( )
A.48° B.58° C.42° D.18°
3.如图,在△ABC中,点D,E,F分别在边BC,AB,AC上,下列不能判定DE∥AC的条件是( )
A.∠3=∠C B.∠1+∠4=180°
C.∠1=∠AFE D.∠1+∠2=180°
4.若∠α=30°30',则它的余角的度数是( )
A.59°10' B.59°30' C.149°10' D.60°10'
5.将一直角三角板与两边平行的纸条如图所示放置,下列结论:①∠1=∠2;②∠3=∠4; ③∠2+∠4=90°;④∠4+∠5=180°,其中正确的个数是( )
A.1 B.2 C.3 D.4
6.将一副三角板按如图所示摆放,其中∠α与∠β一定互余的是( )
A. B.
C. D.
7.一把直尺和一个含30°,60°角的三角板如图所示摆放,直尺一边与三角板的两直角边分别交于F,A两点,另一边与三角板的两直角边分别交于D,E两点,且∠CED=50°,那么∠BAF的大小为( )
A.10° B.20° C.30° D.40°
8.如图,点O是直线AB上一点,OC平分∠AOE,∠DOE=90°,则以下结论:①∠AOD与∠BOE互为余角;②∠AOD∠COE;③∠BOE=2∠COD;④若∠BOE=58°,则∠COE=61°.其中正确的是( )
A.只有①④ B.只有①③④ C.只有③④ D.①②③④
9.如图,a∥b,c⊥d,∠1=25°,则∠2的度数为( )
A.45° B.55° C.65° D.75°
10.如图,∠1=∠2,∠3=∠4,,下列判断:
①射线OF是∠BOE的角平分线;
②∠BOC是∠3的补角;
③∠COD=∠BOE;
④∠3的余角有∠BOE和∠COD.
其中正确的是( )
A.①③④ B.①②③ C.①②③④ D.②③④
二.填空题(共6小题)
11.25°37′的补角为 .
12.若一个角的度数为52°18',则它的补角的度数为 .
13.如图,某同学的家在P处,他想尽快赶到附近C处搭顺风车.他选择了第②条路线,这其中蕴含的数学道理是 .
14.已知∠α和∠β互余,∠α=30°,则∠β= °.
15.如图,AB∥CD,BC∥DE,∠B=72°,则∠D= 度.
16.已知一个角的余角比这个角的补角的一半还小12°,则这个角的度数为 .
三.解答题(共9小题)
17.已知O是直线AB上一点,∠BOC<180°,OD在∠BOC内,OE平分∠BOC.
(1)如图1,当∠AOC=40°,∠COD=60°时,∠DOE的度数是 ;
(2)OF平分∠BOD.
①如图2,试说明∠COD=2∠EOF;
②若∠COF与∠DOE互为补角,求∠COD的度数.
18.计算:
(1)一出租车司机一天下午以希望小学为出发地在东西方向营运,向东走为正,向西走为负,行车里程(单位:km)依先后次序记录如下:+10,﹣6,﹣4,+7,﹣8,+5,﹣3,+3,﹣4,+10.若每千米收费2.8元,求司机这个下午的营业额.
(2)若一个角的补角比它的余角的2倍还多70°,求这个角的度数?
19.如图所示,已知∠AOC=2∠BOC,∠AOC的余角比∠BOC小30°.
(1)求∠AOC的度数;
(2)过点O作射线OD,使得∠AOC=5∠AOD,请你求出∠COD的度数.
20.将一直角三角板的直角顶点放在直线AB上的点O处,过点O作射线OC.
(1)已知∠BOC=60°,
①如图1,当ON在射线OB上时,∠COM的度数为 ;
②如图2,当ON在∠BOC内部时,若,求∠BON的度数;
(2)如图3,∠BOC=α(60°<α<90°),ON在∠BOC内部,∠CON<30°,在图中画射线OH,使OC为∠HON的三等分线,且∠CON<∠COH.当5∠COM﹣∠BOC=270°时,探究∠MOH与∠BON的数量关系,并说明理由.
21.如图是一种躺椅及其简化结构示意图,扶手AB与底座CD都平行于地面,靠背DM与支架OE平行,前支架OE与后支架OF分别与CD交于点G和点D,AB与DM交于点N,当前支架OE与后支架OF正好垂直,∠ODC=32°时,人躺着最舒服,求此时扶手AB与支架OE的夹角∠AOE和扶手AB与靠背DM的夹角∠ANM的度数.
22.【探索与解决】
课本原型
如图(1),点A、O、B在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC.
(1)写出与∠AOD互余的角是 ;
(2)写出与∠AOD互补的角是 ;
(3)∠DOE度数是多少度?请简单写出理由.
【拓展与延伸】
如图(2),点A、O、B不在同一条直线上,射线OD和射线OE分别平分∠AOC和∠BOC.
请你直接写出∠DOE与∠AOB的数量关系.
23.如图,已知∠AOB的补角等于它的余角的10倍.
(1)求∠AOB的度数;
(2)若OD平分∠BOC,∠AOC=3∠BOD,求∠AOD的度数.
24.(1)将一副直角三角板ABC,ADE按如图1所示位置摆放,∠BAC=45°,∠EAD=60°.分别作∠BAE,∠CAD的平分线AM,AN.试求∠MAN的度数;
(2)将三角板ADE从图1位置开始绕点A顺时针旋转到图2所示的位置,AM、AN仍然是∠BAE,∠CAD的平分线.试求∠MAN的度数;
(3)将三角板ADE从图1位置开始绕点A顺时针旋转α°(0°<α<360°),AM、AN仍然是∠BAE,∠CAD的平分线.在旋转的过程中,∠MAN的度数会发生改变吗?请说明理由.
25.综合与探究
问题情境:
数学活动课上,老师以直线AB上一点O为端点作射线OC,OD,OM,ON,使OM平分∠AOC,ON平分∠BOD,若∠COD=α,求∠MOC+∠DON的度数.
特例探究:
(1)从特殊到一般是研究几何的一般思路,如图2,“兴趣小组”将一个三角尺的直角顶点放在点O处,即当∠COD=90°时,则∠MOC+∠DON的度数为 ;(直接写出答案,不写过程)
(2)受“兴趣小组”的启发,“智慧小组”将三角尺60°角的顶点放在点O处,即当∠COD=60°时,请你在图3中求∠MOC+∠DON的度数;
数学思考:
(3)请你在图1中,求∠MOC+∠DON的度数(用含有α的式子表示).
第二章 相交线与平行线
参考答案与试题解析
一.选择题(共10小题)
1.【答案】B
【分析】根据两直线平行,内错角相等得出∠A的度数,再根据三角形外角的性质即可求出∠AOB的度数,最后根据对顶角的性质即可求出∠COD的度数.
【解答】解:∵AB∥CD,∠ADC=50°,
∴∠A=∠ADC=50°,
∵∠ABE是△AOB的外角,∠ABE=125°,
∴∠AOB=∠ABE﹣∠A=125°﹣50°=75°,
∴∠COD=∠AOB=75°,
故选:B.
【点评】本题考查了平行线的性质,三角形外角的性质,对顶角的性质,熟练掌握这些知识点是解题的关键.
2.【答案】A
【分析】根据平行的性质可得∠DEB=∠1=72°,根据三角形的外角的定义可得∠ADC=42°,再根据平角进行计算即可得到答案.
【解答】解:如图,设AB与l1相交于点E,
∵l1∥l2,∠1=72°,
∴∠DEB=∠1=72°,
∵∠A+∠ADC=∠DEB=72°,∠A=30°,
∴∠ADE=42°,
∵∠ADC+∠BDE+∠2=180°,BD⊥l2,
∴∠2=48°.
故选:A.
【点评】本题主要考查了平行线的性质、三角形外角的定义,平角的定义,熟练掌握平行线的性质、三角形外角的定义,平角的定义是解题的关键.
3.【答案】D
【分析】利用平行线的判定方法分别分析得出答案.
【解答】解:A、当∠C=∠3时,DE∥AC,故不符合题意;
B、当∠1+∠4=180°时,DE∥AC,故不符合题意;
C、当∠1=∠AFE时,DE∥AC,故不符合题意;
D、当∠1+∠2=180°时,EF∥BC,不能判定DE∥AC,故符合题意.
故选:D.
【点评】本题主要考查了平行线的判定,正确掌握平行线的判定方法是解题关键.
4.【答案】B
【分析】互余两角的和等于90°,90°与∠α的差,就是它的余角.
【解答】解:90°﹣∠α=90°﹣30°30′=59°30′.
故答案为:B.
【点评】本题考查了两角互为余角的定义,度分秒换算,关键是两角减法,1°=60′.
5.【答案】D
【分析】根据平行线的性质,直角三角板的性质对各小题进行验证即可得解.
【解答】解:∵纸条的两边互相平行,
∴∠1=∠2,∠3=∠4,∠4+∠5=180°,故①,②,④正确;
∵三角板是直角三角板,
∴∠2+∠4=180°﹣90°=90°,故③正确.
综上所述,正确的个数是4.
故选:D.
【点评】本题考查了平行线的性质,直角三角板的性质,熟记性质与概念并准确识图是解题的关键.
6.【答案】A
【分析】根据每个图形中∠α与∠β的关系进行判断,即可找出一定互余的图形.
【解答】解:A中的∠α与∠β的和等于平角减去一个直角,是90°,故A中的∠α与∠β一定互余;
B中的∠α与∠β是同一个角的余角,一定相等,但是不一定互余,故B排除;
C中∠α与∠β都是钝角,不可能互余,故C排除;
D中∠α与∠β互为邻补,不可能互余,故D排除.
故选:A.
【点评】本题主要考查余角,熟练掌握互为余角的定义是解决问题的关键.
7.【答案】A
【分析】先根据∠CED=50°,DE∥AF,即可得到∠CAF=50°,最后根据∠BAC=60°,即可得出∠BAF的大小.
【解答】解:∵DE∥AF,∠CED=50°,
∴∠CAF=∠CED=50°,
∵∠BAC=60°,
∴∠BAF=60°﹣50°=10°,
故选:A.
【点评】本题主要考查了平行线的性质以及直角三角形的性质的运用,解题解题的关键是掌握平行线的性质:两直线平行,同位角相等.
8.【答案】B
【分析】根据补角以及角平分线的定义解决此题.
【解答】解:①由∠DOE=90°,得∠AOD+∠BOE=180°﹣∠DOE=90°,那么∠AOD与∠BOE互为余角,故①正确.
②由OC平分∠AOE,得∠AOC=∠COE,无法推断得到∠AOD∠COE,故②错误.
③设∠COD=x,由∠DOE=90°,得∠COE=90°﹣x.由OC平分∠AOE,得∠AOC=∠COE,那么∠AOD=90°﹣2x,进而推断出∠BOE=2x,也就是说∠BOE=2∠COD,故③正确.
④由∠BOE=58°,得∠AOE=180°﹣∠BOE=122°.由OC平分∠AOE,得∠COE61°,故④正确.
综上:正确的有①③④.
故选:B.
【点评】本题主要考查角平分线、补角,熟练掌握角平分线的定义以及补角的定义是解决本题的关键.
9.【答案】C
【分析】先利用垂直性质求∠3度数,再利用平行线性质求∠2度数.
【解答】解:如图:
∵c⊥d,
∴∠1+∠3=90°,
∵∠1=25°,
∴∠3=65°,
∵a∥b,
∠2=∠3=65°.
故选:C.
【点评】本题考查了平行线的性质,掌握平行线的性质是解题关键.
10.【答案】C
【分析】根据角平分线的定义和互为余角、互为补角的定义判断即可.
【解答】解:①∵∠1=∠2,∴射线OF是∠BOE的角平分线,故正确;
②∵∠BOC+∠4=180°,又∵∠3=∠4,∴∠BOC+∠3=180°,即∠BOC是∠3的补角,故正确;
③∵,∴∠AOD=90°,∠BOE+∠3=90°,∴∠4+∠COD=90°,∵∠3=∠4,∴∠COD=∠BOE,故正确;
④∠3的余角有∠BOE和∠COD,故正确.
正确的是①②③④,
故选:C.
【点评】本题考查了余角和补角,角平分线的定义,正确识别图形是解题的关键.
二.填空题(共6小题)
11.【答案】154°23′.
【分析】根据互为补角的定义,列出算式,进行计算即可.
【解答】解:25°37′的补角为:
180°﹣25°37′
=179°60′﹣25°37′
=154°23′,
故答案为:154°23′.
【点评】本题主要考查了互为补角定义和度分秒的换算,解题关键是熟练掌握互为补角的两个角的和为180°.
12.【答案】127°42'.
【分析】如果两个角的和为180°,那么这两个角互为补角;由此计算即可.
【解答】解:若一个角的度数为52°18',
则它的补角的度数为180°﹣52°18'=179°60'﹣52°18'=127°42',
故答案为:127°42'.
【点评】本题考查了余角和补角,度分秒的换算,熟知互为补角的定义是解题的关键.
13.【答案】两点之间,线段最短.
【分析】根据两点之间,线段最短进行判断即可.
【解答】解:在点P与点C之间所有的连线中,线段最短,即两点之间,线段最短.
故答案为:两点之间,线段最短.
【点评】本题考查线段的性质,掌握两点之间,线段最短是正确判断的关键.
14.【答案】见试题解答内容
【分析】根据余角的定义计算.
【解答】解:已知∠α和∠β互余,∠α=30°,
则∠β=90°﹣∠α=60°.
故答案为:60.
【点评】本题考查余角的定义:如果两个角的和为90°,则这两个角互为余角.
15.【答案】见试题解答内容
【分析】先根据AB∥CD求出∠C的度数,再由BC∥DE即可求出∠D的度数.
【解答】解:∵AB∥CD,∠B=72°,
∴∠C=∠B=72°,
∵BC∥DE,
∴∠D=180°﹣∠C=180°﹣72°=108°.
故答案为:108.
【点评】本题考查的是平行线的性质,即两直线平行,内错角相等,同旁内角互补.
16.【答案】24°.
【分析】设这个角为x,则它的余角是90°﹣x,它的补角是180°﹣x,列方程求解即可.
【解答】解:设这个角为x,
则它的余角是90°﹣x,它的补角是180°﹣x,
由题意,得:90°﹣x+12°(180°﹣x),
解得:x=24°,
即这个角的度数是24°.
故答案为:24°.
【点评】本题考查了余角和补角,掌握互余的两角之和为90°,互补的两角之和为180°是解题的关键.
三.解答题(共9小题)
17.【答案】(1)10°;
(2)①证明见解析;
②120°.
【分析】(1)根据平角定义和已知条件,求出∠BOC,再根据角平分线的定义先求出∠COE的度数,再减去∠COD的度数即可;
(2)①先根据角平分线的定义证明∠COE=∠DOB,∠DOF=∠BOF,然后根据∠COD=∠COE+∠DOF,最后代换成2(∠DOE+∠DOF)进行解答即可;
②先根据已知条件得到∠COF+∠DOE=180°,从而得到∠COD+∠DOF+∠DOE=180°,根据①的结论,得到关于∠EOF的方程,求出∠EOF,再求出∠COD即可.
【解答】解:(1)∵O是直线AB上一点,
∴∠AOC+∠BOC=180°,
∵∠AOC=40°,
∴∠BOC=180°﹣40°=140°,
∵OE平分∠BOC,
∴∠COE,
∵∠COD=60°,
∴∠DOE=∠COE﹣∠COD=70°﹣60°=10°,
故答案为:10°;
(2)证明:①∵OE平分∠BOC,
∴∠COE=∠DOB,
∵OF平分∠BOD,
∴∠DOF=∠BOF,
∵∠COD=∠COE+∠DOE,
∴∠COD=∠BOE+∠DOE
=∠DOE+∠DOF+∠BOF+∠DOE,
=∠DOE+∠DOF+∠DOF+∠DOE
=2∠DOE+2∠DOF
=2(∠DOE+∠DOF)
=2∠EOF;
②∵∠COF与∠DOE互为补角,
∴∠COF+∠DOE=180°,
∴∠COD+∠DOF+∠DOE=180°,
∠COD+∠EOF=180°,
2∠EOF+∠EOF=180°,
3∠EOF=180°,
∴∠EOF=60°,
∴∠COD=2∠EOF=120°.
【点评】本题主要考查了角的有关运算,解题关键是正确识别图形,理解角与角之间的和差倍分关系.
18.【答案】(1)168元;
(2)70°.
【分析】(1)把每次行车里程相加求出这天下午的总里程,然后乘单价即可求出司机这个下午的营业额;
(2)设这个角为x,分别表示出其补角和余角,根据题意列出方程然后解方程即可求出这个角的度数.
【解答】解:(1)10+6+4+7+8+5+3+3+4+10=60(km),
2.8×60=168(元).
答:司机这个下午的营业额为168元.
(2)设这个角为x,则其补角度数为180°﹣x,余角度数为90°﹣x,
由题意得:180°﹣x=2(90°﹣x)+70,
解得:x=70°,
∴这个角的度数为70°.
【点评】本题主要考查正数和负数以及余角和补角,熟练掌握正负数的意义和求一个角余角、补角的方法是解决问题的关键.
19.【答案】(1)∠AOC=80°;
(2)64°或96°.
【分析】(1)设∠BOC=x,则∠AOC=2x,根据,∠AOC的余角比∠BOC小30°列方程求解即可;
(2)分两种情况:①当射线OD在∠AOC内部②当射线OD在∠AOC外部,分别求出∠COD的度数即可.
【解答】解:(1)设∠BOC=x,则∠AOC=2x,
依题意列方程90°﹣2x=x﹣30°,
解得:x=40°,
即∠AOC=40°×2=80°.
(2)由(1)得,∠AOC=80°,
①当射线OD在∠AOC内部时,∠AOD=16°,
则∠COD=∠AOC﹣∠AOD=80°﹣16°=64°;
②当射线OD在∠AOC外部时,∠AOD=16°,
则∠COD=∠AOC+∠AOD=80°+16°=96°.
【点评】本题考查了余角和补角的知识,解答本题的关键是掌握互余两角之和为90°,互补两角之和为180°.
20.【答案】(1)①30°;
②55°;
(2)∠BON=2∠HOM.理由见解析.
【分析】(1)①根据余角的定义即可得到结论;
②设∠CON=α,∠AOM=6α,求得∠BON=60°﹣α,列方程得到α=5°,于是得到∠BON=60°﹣5°=55°;
(2)根据OC为∠HON的三等分线,设∠CON=β,∠COH=2β,得到∠BON=α﹣β,∠COM=90°﹣β,列方程得到α=180°﹣5β,于是得到∠BON=2∠HOM.
【解答】解:(1)①∵∠BOM=90°,∠BOC=60°,
∴∠COM=90°﹣60°=30°;
故答案为:30°;
②∵,
∴设∠CON=α,∠AOM=6α,
∵∠BOC=60°,
∴∠BON=60°﹣α,
∴∠AOM=180°﹣90°﹣(60°﹣α)=6α,
∴α=5°,
∴∠BON=60°﹣5°=55°;
(2)∠BON=2∠HOM.
理由:如图,
∵OC为∠HON的三等分线,
∴设∠CON=β,∠COH=2β,
∵∠BOC=α,
∴∠BON=α﹣β,
∴∠COM=90°﹣β,
∵5∠COM﹣∠BOC=270°,
∴5(90°﹣β)﹣α=270°,
∴α=180°﹣5β,
∴∠BON=∠BOC﹣∠CON=180°﹣6β=2(90°﹣3β),
∵∠HOM=90°﹣∠COH﹣∠CON=90°﹣3β,
∴∠BON=2∠HOM.
【点评】本题考查了余角与补角,一元一次方程的应用,正确的识别图形是解题的关键.
21.【答案】122°.
【分析】先根据平行线的性质,得出∠ODC=∠BOD=32°,再根据∠EOF=90°,即可得到∠AOE=58°,再根据平行线的性质,即可得到∠AND的度数,进而得出∠ANM的度数.
【解答】解:∵扶手AB与底座CD都平行于地面,
∴AB∥CD,
∴∠ODC=∠BOD=32°,
又∵∠EOF=90°,
∴∠AOE=58°,
∵DM∥OE,
∴∠AND=∠AOE=58°,
∴∠ANM=180°﹣∠AND=122°.
【点评】本题主要考查了平行线的性质的运用,掌握两直线平行,内错角相等;两直线平行,同位角相等是解题的关键.
22.【答案】【探索与解决】(1)∠COE,∠BOE;
(2)∠BOD;
(3)∠DOE=90°;
理由见解析;
【拓展与延伸】∠COD∠AOB.
【分析】【探索与解决】(1)根据角平分线的定义得到∠COD=∠AOD∠AOC,∠COE=∠BOE∠BOC,于是得到∠AOD与∠COE互为余角,∠AOD与∠BOE互为余角;
(2)根据互为补角的定义即可得到结论;
(3)根据角平分线的定义和角的和差即可得到结论;
【拓展与延伸】根据角平分线的定义和角的和差即可得到结论.
【解答】解:【探索与解决】(1)∵点A,O,B在同一条直线上,
∵射线OD和射线OE分别平分∠AOC和∠BOC,
∴∠COD=∠AOD∠AOC,∠COE=∠BOE∠BOC,
∴∠COD+∠COE∠AOC∠BOC180°=90°.
∴∠AOD与∠COE互为余角,∠AOD与∠BOE互为余角;
故答案为:∠COE,∠BOE;
(2)∠AOD与∠BOD分别互为补角,
故答案为:∠BOD;
(3)∠DOE=90°;
理由:∵射线OD和射线OE分别平分∠AOC和∠BOC,
∴∠COD=∠AOD∠AOC,∠COE=∠BOE∠BOC,
∴∠COD+∠COE∠AOC∠BOC180°=90°,
∴∠DOE=90°;
【拓展与延伸】∵射线OD和射线OE分别平分∠AOC和∠BOC,
∴∠COD=∠AOD∠AOC,∠COE=∠BOE∠BOC,
∴∠COD+∠COE∠AOC∠BOCAOB.
【点评】本题主要考查补角与余角、角平分线,熟练掌握补角与余角、角平分线的定义是解决本题的关键.
23.【答案】(1)80°.
(2)160°.
【分析】(1)利用设元法列方程求解即可.
(2)设∠BOD=y,利用题目条件列出关于y的方程求解即可.
【解答】解:(1)设∠AOB=x,
由题意得:180°﹣x=10(90°﹣x),
解得x=80°.
所以∠AOB的度数为80°.
(2)设∠BOD=y,则∠AOC=3y,
∵OD平分∠BOC,
∴∠BOC=2∠BOD=2y,
由题意得:2y+80°=3y°,
解得y=80°,
∴∠AOD=∠AOB+∠BOD=80°+80°=160°.
【点评】本题考查角度的计算、补角和余角的概念,熟练掌握设元法求角的方法是解题关键.
24.【答案】(1)52.5°;(2)52.5°;(3)不变,理由见详解.
【分析】(1)根据题意求得∠MAE、∠NAE,再相加即可;
(2)用已知60°、45°、∠DAB来分别表示∠MAB、∠NAD,再减去∠DAB即可;
(3)通过画图考虑到∠BAE.∠CAD为钝角时的情况,根据(2)的思路解答即可.
【解答】解:(1)∵AM,AN是∠BAE,∠CAD的平分线,
∴∠MAE=22.5°,∠NAE=30°,
∴∠MAN=∠MAE+∠NAE=22.5°+30°=52.5°.
(2)∠MAB;,
∠MAN=∠MAB+∠NAD﹣∠BAD∠BAD=30°+22.5=52.5°;
(3)不变,在旋转过程中,∠BAE.∠CAD为钝角时,如图示:
∵∠MAE,,
∴∠MAN=∠MAE+∠NAC﹣∠CAE∠CAE=52.5°.
【点评】本题考查了角平分线的定义,熟练掌握角平分线的定义是解答本题的关键.
25.【答案】(1)45°;(2)60°;(3).
【分析】(1)求得∠AOC+∠BOD=90°,利用角平分线的定义得,据此求解即可;
(2)求得∠AOC+∠BOD=120°,利用角平分线的定义得,据此求解即可;
(3)求得∠AOC+∠BOD=180°﹣α,利用角平分线的定义得求解即可.
【解答】解:(1)因为∠COD=90°,所以∠AOC+∠BOD=90°,
因为OM平分∠AOC,ON平分∠BOD,
所以,,
所以
;
故答案为:45°;
(2)因为∠COD=60°,所以∠AOC+∠BOD=120°,
因为OM平分∠AOC,ON平分∠BOD,
所以,,
所以
;
(3)因为∠COD=α,所以∠AOC+∠BOD=180°﹣α,
因为OM平分∠AOC,ON平分∠BOD,
所以,,
所以
.
【点评】本题考查角度计算,涉及角平分线的定义,解题的关键是根据题意得到.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
