第六章 变量之间的关系(巩固复习.培优卷.含解析)-2024-2025学年北师大版(2024)数学七年级下册
文档属性
| 名称 | 第六章 变量之间的关系(巩固复习.培优卷.含解析)-2024-2025学年北师大版(2024)数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 481.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-21 16:10:20 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
第六章 变量之间的关系
一.选择题(共8小题)
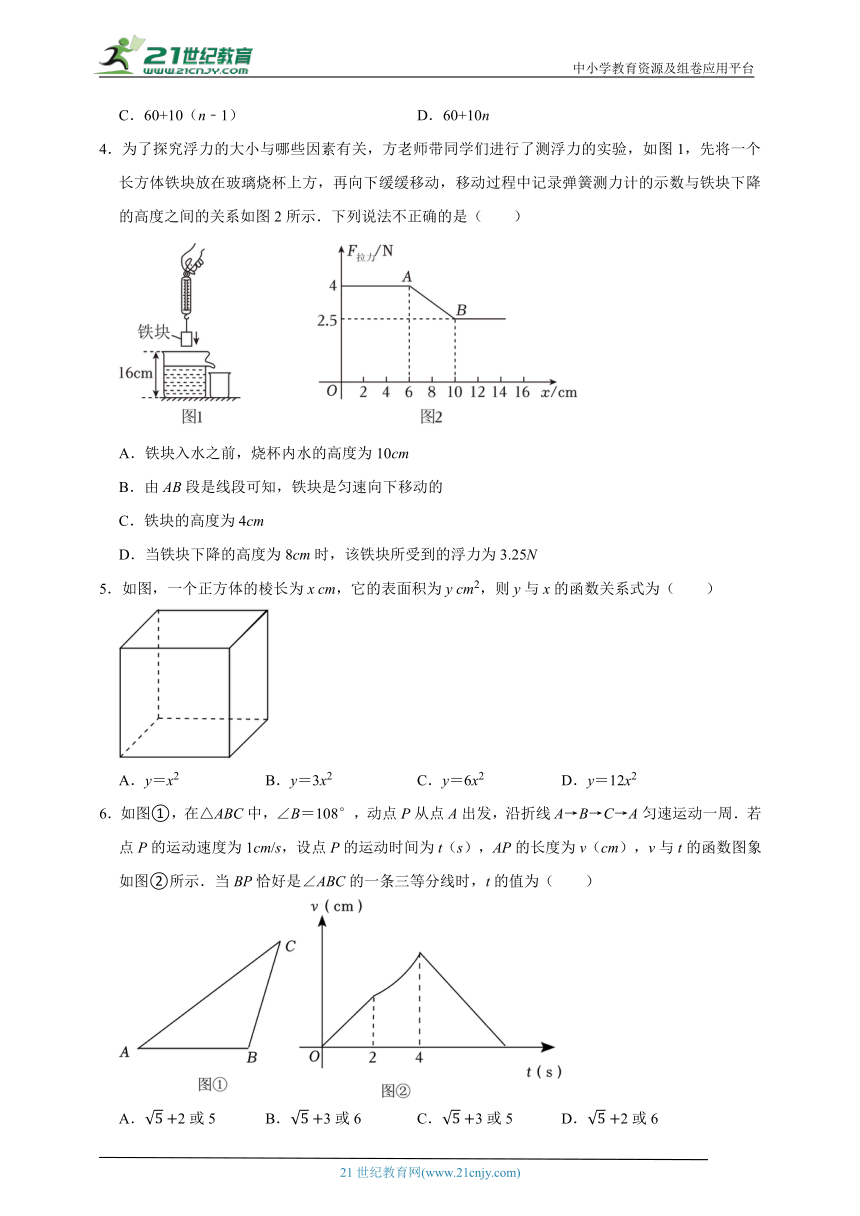
1.在测浮力的实验中,将一长方体石块由玻璃器皿的上方,向下缓慢移动浸入水里的过程中,弹簧测力计的示数F拉力(N)与石块下降的高度x(cm)之间的关系如图所示.(温馨提示:当石块位于水面上方时,F拉力=G重力,当石块入水后,F拉力=C重力﹣F浮力.)则以下说法正确的是( )
A.当石块下降3cm时,此时石块在水里
B.当6≤x≤10时,F拉力(N)与x(cm)之间的函数表达式为F拉力
C.石块下降高度8cm时,此时石块所受浮力是1N
D.当弹簧测力计的示数为3N时,此时石块距离水底
2.甲、乙两车从A城出发前往B城,过程中,汽车离开A城的距离y(km)与时刻t的关系如图所示,则被墨水遮住的时刻是( )
A.7:20 B.7:30 C.7:45 D.8:00
3.某树苗原始高度为60cm,如图是该树苗的高度与生长的月数的有关数据示意图,假设以后一段时间内,该树苗高度的变化与月数保持此关系,用式子表示生长n个月时,它的高度(单位:cm)应为( )
A.60+5(n﹣1) B.60+5n
C.60+10(n﹣1) D.60+10n
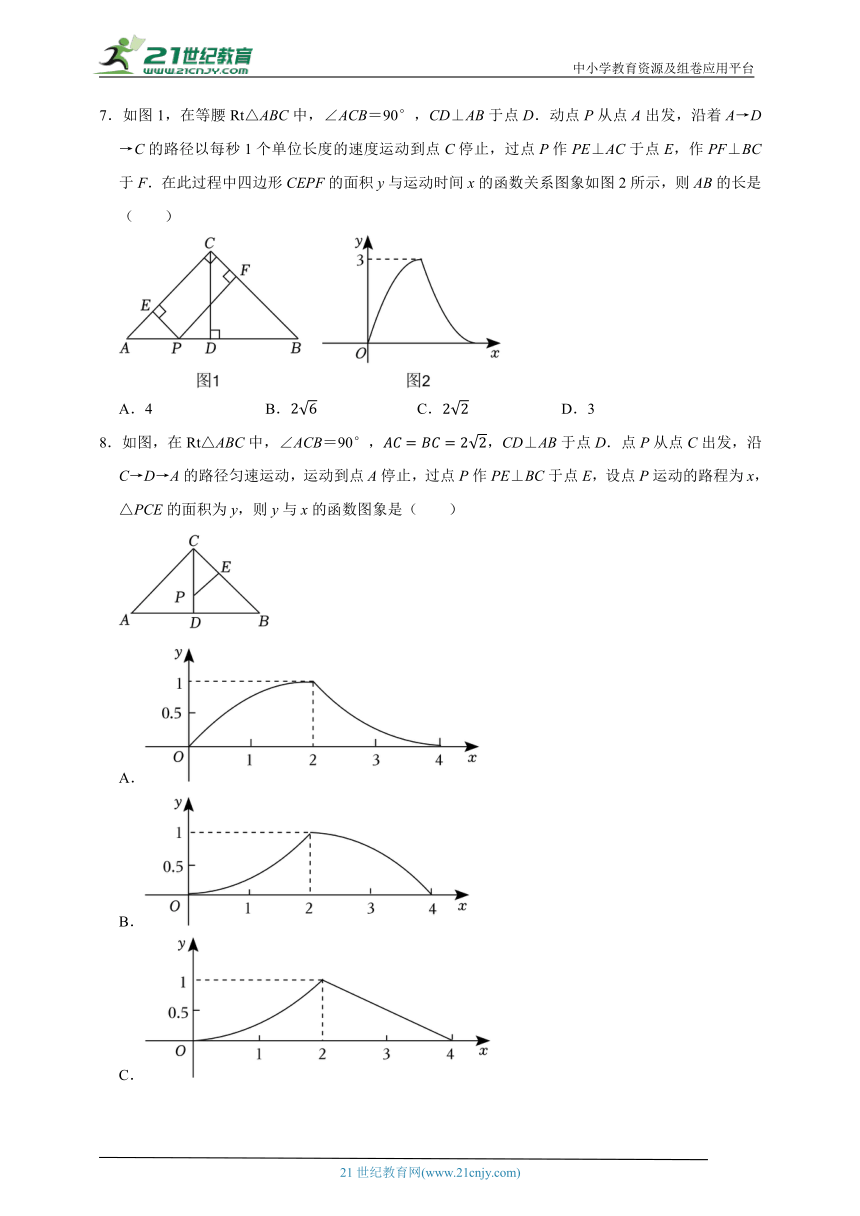
4.为了探究浮力的大小与哪些因素有关,方老师带同学们进行了测浮力的实验,如图1,先将一个长方体铁块放在玻璃烧杯上方,再向下缓缓移动,移动过程中记录弹簧测力计的示数与铁块下降的高度之间的关系如图2所示.下列说法不正确的是( )
A.铁块入水之前,烧杯内水的高度为10cm
B.由AB段是线段可知,铁块是匀速向下移动的
C.铁块的高度为4cm
D.当铁块下降的高度为8cm时,该铁块所受到的浮力为3.25N
5.如图,一个正方体的棱长为x cm,它的表面积为y cm2,则y与x的函数关系式为( )
A.y=x2 B.y=3x2 C.y=6x2 D.y=12x2
6.如图①,在△ABC中,∠B=108°,动点P从点A出发,沿折线A→B→C→A匀速运动一周.若点P的运动速度为1cm/s,设点P的运动时间为t(s),AP的长度为v(cm),v与t的函数图象如图②所示.当BP恰好是∠ABC的一条三等分线时,t的值为( )
A.2或5 B.3或6 C.3或5 D.2或6
7.如图1,在等腰Rt△ABC中,∠ACB=90°,CD⊥AB于点D.动点P从点A出发,沿着A→D→C的路径以每秒1个单位长度的速度运动到点C停止,过点P作PE⊥AC于点E,作PF⊥BC于F.在此过程中四边形CEPF的面积y与运动时间x的函数关系图象如图2所示,则AB的长是( )
A.4 B. C. D.3
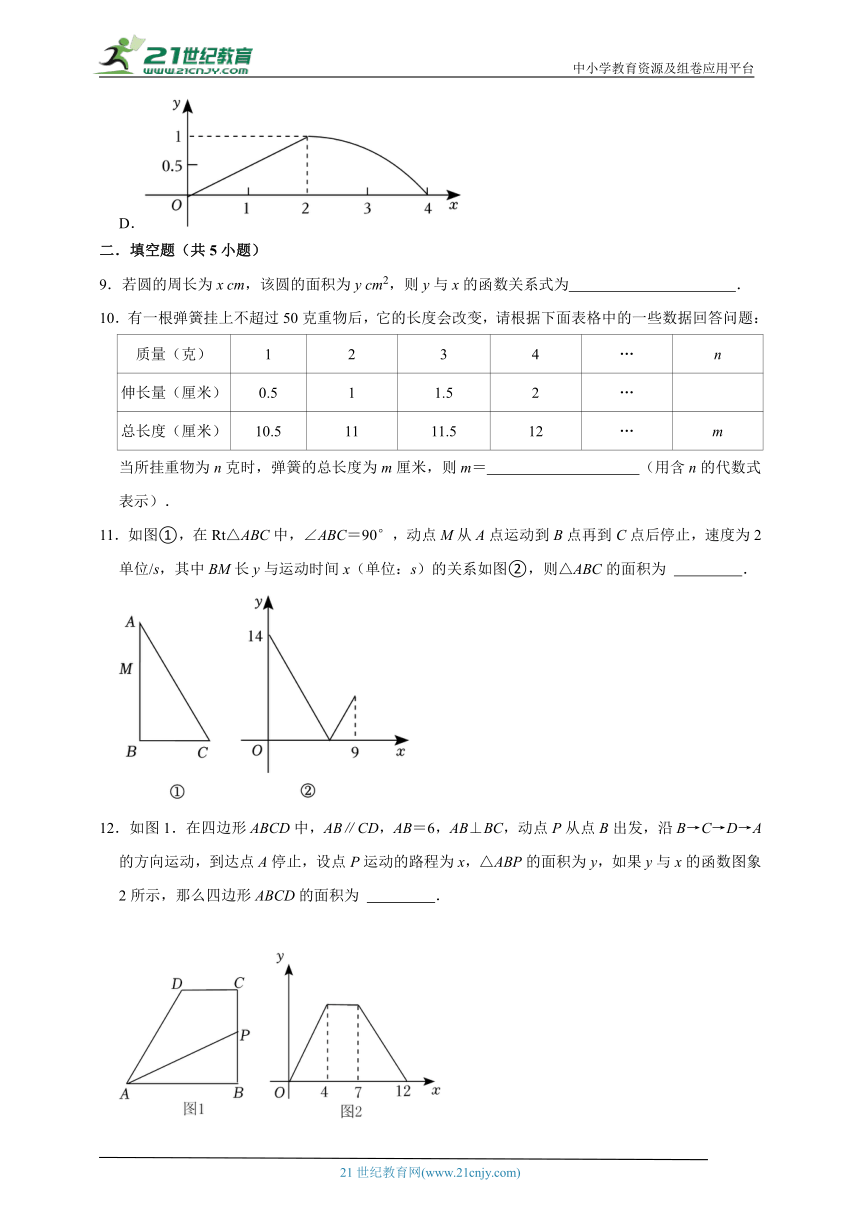
8.如图,在Rt△ABC中,∠ACB=90°,,CD⊥AB于点D.点P从点C出发,沿C→D→A的路径匀速运动,运动到点A停止,过点P作PE⊥BC于点E,设点P运动的路程为x,△PCE的面积为y,则y与x的函数图象是( )
A.
B.
C.
D.
二.填空题(共5小题)
9.若圆的周长为x cm,该圆的面积为y cm2,则y与x的函数关系式为 .
10.有一根弹簧挂上不超过50克重物后,它的长度会改变,请根据下面表格中的一些数据回答问题:
质量(克) 1 2 3 4 … n
伸长量(厘米) 0.5 1 1.5 2 …
总长度(厘米) 10.5 11 11.5 12 … m
当所挂重物为n克时,弹簧的总长度为m厘米,则m= (用含n的代数式表示).
11.如图①,在Rt△ABC中,∠ABC=90°,动点M从A点运动到B点再到C点后停止,速度为2单位/s,其中BM长y与运动时间x(单位:s)的关系如图②,则△ABC的面积为 .
12.如图1.在四边形ABCD中,AB∥CD,AB=6,AB⊥BC,动点P从点B出发,沿B→C→D→A的方向运动,到达点A停止,设点P运动的路程为x,△ABP的面积为y,如果y与x的函数图象2所示,那么四边形ABCD的面积为 .
13.在如图所示的计算程序中,输入一个有理数x,便可输出一个相应的有理数y,则y与x之间的关系式是 .
三.解答题(共9小题)
14.如图1,AD是三角形ABC的边BC上的高,且AD=8cm,BC=9cm,点E从点B出发,沿线段BC向终点C运动,其速度与时间的关系如图2所示,设点E运动时间为x(s),三角形ABE的面积为y(cm2).
(1)在点E沿BC向点C运动的过程中,它的速度是 cm/s,用含x的代数式表示线段BE的长是 cm,变量y与x之间的关系式为 ;
(2)当x=2时,y的值为 ;当x每增加1s时,y的变化情况是: .
15.经过实验获得两个变量x(x>0),y(y>0)的一组对应值如表.
x 1 2 3 4 5
y 6 3 2 1.5 1.2
(1)请在如图所示的平面直角坐标系中画出相应函数的图象;
(2)求出函数表达式;
(3)点A(x1,y2),B(x2,y2)在此函数图象上,若0<x1<x2,则y1,y2有怎样的大小关系?
16.某网上购物平台促销,苹果2千克以上有优惠(不含2千克),购买苹果所付金额(元)与购买数量(千克)之间的关系如图所示,根据图象回答下列问题:
(1)购买1千克苹果多少元?
(2)购买3千克苹果多少元?
(3)一次性下单购买苹果6千克与平均分3次下单购买可节省多少元?
17.如图1,在长方形ABCD中,AB:AD=3:5,点P从点A出发以2cm/秒的速度沿A→B→C→D的路线匀速移动.随着点P的移动,三角形APD的面积会不断发生变化,它的面积变化情况如图2所示.
(1)点P从点A出发,经过多少秒后到达点D?
(2)点P从点A出发,经过多少秒后三角形APD的面积恰好是25cm2?
18.某市为了节约用水,采用分段收费标准,设居民每月应交水费为y(元),用水量为x(立方米).
用水量(立方米) 收费(元)
不超过10立方米 每立方米2.5元
超过10立方米 超过的部分每立方米3.5元
(1)写出每月用水量不超过10立方米和超过10立方米时,水费与用水量之间的关系式:
①每月用水量不超过10立方米时,y= ;
②每月用水量超过10立方米时,y= ;
(2)若某户居民某月用水量为6立方米,则应交水费多少元?
(3)若某户居民某月交水费32元,则该户居民用水多少立方米?
19.为增强公民的节约意识,合理利用天然气资源,我市将居民用天然气用气量及价格分为三档,其中:
档次 年用气量 单价(元/m3)
第一档气量 不超出300m3的部分 2.7
第二档气量 超出300m3不超出600m3的部分 a
第三档气量 超出600m3的部分 a+0.5
(说明:户籍人口超过4人的家庭,每增加1人,各档年用气量基数按每人增加60立方米依次调整)
(1)若甲用户户籍人口登记有4人,今年前三个月已使用天然气200m3,则应缴费 元.
(2)若乙用户户籍人口登记有5人,今年已使用天然气560m3,则应缴费 元.(用含a的代数式表示)
(3)若丙用户户籍人口登记有5人,今年该用户年用气量为x(m3),当a=3.3时请用含x的代数式表示丙用户一年支出的燃气费.
20.根据实验测定:高度每增加1000米,气温大约变化量为﹣6℃.
(1)若某登山运动员攀登了3000米,则气温变化量为多少?
(2)若某登山运动员在攀登途中发回信息,报告他所在高度的气温为﹣27℃,如果当时地面温度为6℃,求此时该登山运动员攀登了多少米?
21.如图1,已知∠MQN,QA、QB分别从QM、QN同时开始旋转,QA按逆时针方向旋转,旋转到与QN重合时停止旋转,QB按顺时针方向旋转,旋转到与QM重合后,立刻按原速度逆时针返回,与QN重合停止旋转.根据观察,QA、QB最终同时停止旋转,旋转过程中∠AQB的大小记作y(°),旋转时间记作t(s),y与t之间的关系如图2所示.
(1)依据图象,请直接填写:∠MQN= °;QA旋转的速度是 °/s;a+b= ;
(2)当∠AQB=40°时,求旋转时间t的值.
22.已知琳琳家、药店、邮局在同一直线上,琳琳从家出发,跑步去药店买了酒精和口罩,又步行到邮局把物品寄出,然后走回家.琳琳离家的距离y(km)与时间x(min)之间的关系如图所示,请根据图象解决下列问题:
(1)琳琳家离药店的距离为 km;
(2)琳琳邮寄物品用了 min;
(3)求琳琳从邮局走回家的速度是多少?
第六章 变量之间的关系
参考答案与试题解析
一.选择题(共8小题)
1.【答案】D
【分析】观察图象,解出6≤x10的函数关系式,利用关系式判断出相关结论即可解题.
【解答】解:A、由图得,当石块下降3cm时,拉力不变,此时石块不在水里,故A不符题意;
B、设F=kx+b,代入(6,4)(10,2.5),得Fx,故B不符合题意;
C、将x=8代入Fx,得F,4,故C不符合题意;
D、将F=3代入Fx,得x,16,故D符合题意;
故选:D.
【点评】本题考查了函数图象的应用,对物理常识的掌握及数形结合的思想是解题关键.
2.【答案】B
【分析】根据题意可得甲和乙的速度,据此可得乙追上甲的数据,进而得出答案.
【解答】解:甲的速度为:300÷(10﹣5)=60(km/h),
乙的速度为:300÷(9﹣6)=100(km/h),
设乙用了x小时追上甲,根据题意得:
100x=60×(x+1),
解得x=1.5,
即乙用了1.5小时追上甲,
所以被墨水遮住的时刻是7:30.
故选:B.
【点评】本题考查了函数的图象.主要利用了路程、速度、时间三者之间的关系,准确识图,理解横、纵坐标的实际意义是解题的关键.
3.【答案】D
【分析】由题意可得树苗每个月增长的高度是10cm,进而得出答案.
【解答】解:根据题意可得,树苗每个月增长的高度是10cm,
∴用式子表示生长n个月时,它的高度(单位:cm)应为:(60+10n)cm.
故选:D.
【点评】本题考查了函数的图象,得出树苗每个月增长的高度是解答本题的关键.
4.【答案】D
【分析】图2中点(0,4)表示铁块未移动时,拉力为4N,那么铁块的重力为4N,此时铁块下表面与烧杯上端平齐;(6,4)表示铁块向下移动6cm时,拉力为4N,此时铁块下表面与水面平齐;铁块继续向下移动,水向外流出,水平面保持不变.(10,2.5)表示铁块上表面刚好浸入水中,拉力为2.5N.烧杯高度为16cm,铁块下表面接触水时移动了6cm,所以烧杯内水的高度为10cm,可判断A正确,不符合题意;由AB段是线段可知,拉力与移动的距离成一次函数关系,铁块是匀速向下移动的,可判断B正确,不符合题意;AB段表示铁块下表面刚接触水到铁块上表面刚好浸入水中的过程,因为水平面保持不变.那么AB段铁块移动的距离即为铁块的高度,为10﹣6等于4cm,可判断C正确,不符合题意;当铁块下降高度为8cm时,由于出水口的存在,由图2和B选项可知,铁块的一半刚好浸入水中,拉力的大小为3.25N,那么所受到的浮力=重力﹣拉力=4﹣3.25=0.75N,故D错误,符合题意.
【解答】解:∵烧杯高度为16cm,铁块从烧杯口到下表面接触水时移动了6cm,∴烧杯内水的高度为10cm,故A正确,不符合题意;
∵AB段是线段,∴拉力与移动的距离成一次函数关系,∴铁块是匀速向下移动的,故B正确,不符合题意;
∵烧杯有出水口,∴水平面在铁块下移过程中保持不变.∴铁块的高度为AB段铁块移动的距离为10﹣6=4cm,故C正确,不符合题意;
∵当铁块下降高度为8cm时,铁块的一半刚好浸入水中,∴拉力的大小为3.25N,∵铁块的重力为4N,∴铁块所受到的浮力为4﹣3.25=0.75N,故D错误,符合题意.
故选:D.
【点评】本题考查动点问题的函数图象.关键是得到图象中关键点表示的意义.用到的知识点为:浮力=重力﹣拉力.
5.【答案】C
【分析】正方体有6个面,每一个面都是边长为x的正方形,这6个正方形的面积和就是该正方体的表面积.
【解答】解:由题意得,y=6x2,
故选:C.
【点评】本题考查函数关系式,理解两个变量之间的关系是得出关系式的关键.
6.【答案】B
【分析】根据图②可知,AB=BC=2,再根据BP,BP′是∠ABC的三等分线,可以证明△PBC∽△BAC,求出PC的长,即可求出答案.
【解答】解:如图①,BP,BP′是∠ABC的三等分线,
根据图②可知,AB=BC=2,
∵∠ABC=108°,AB=BC,
∴∠A=∠C=∠ABP′=∠CBP=∠PBP′=36°,
∴∠APB=∠ABP=72°,
∴AB=AP=2,
同理CP′=BC=2,
∵∠PBC=∠A,∠C=∠C,
∴△PBC∽△BAC,
∴,
∴,
∴PC1或1(负值舍去),
∴AB+BC+PC3,AB+BC+CP′=6,
∴当BP恰好是∠ABC的一条三等分线时,t的值为3或6.
故选:B.
【点评】本题是动点问题的函数图象,考查了等腰三角形的性质,相似三角形的判定和性质,证明三角形相似是解题的关键.
7.【答案】B
【分析】图2中拐点的纵坐标3,即四边形CEPF的面积y=3,此时点P运动到点D.可证明四边形CEPF是正方形,面积为3,那么正方形的边长AP为.易得△AEP为等腰直角三角形,所以AP长,那么可得AB长度为2.
【解答】解:∵动点P从点A出发,沿着A→D→C的路径运动,
∴第一个拐点的位置在点D处,此时点P运动到点D.
∵图2中拐点的纵坐标3,
∴四边形CEPF的面积为3.
∵PE⊥AC,PF⊥BC,
∴∠CED=∠CFD=∠AED=90°.
∵∠ACB=90°,
∴四边形CEPF是矩形.
∵△ABC是等腰直角三角形,CD⊥AB,
∴∠ACD=∠BCD,∠A=45°,AB=2AP.
∴DE=DF,∠ADE=45°
∴四边形CEPF是正方形,AE=PE.
∴△AED是等腰直角三角形.
∵四边形CEPF的面积为3,
∴PE.
∴AP.
∴AB=2AP=2.
故选:B.
【点评】本题考查了动点问题的函数图象.关键是得到拐点的纵坐标表示的意义及动点此时所在的位置.用到的知识点为:等腰直角三角形的斜边长=直角边边长的倍.
8.【答案】B
【分析】根据题意可知,需要分两种情况,当点P在CD上时,当点P在DA上时,根据三角形的面积公式可得出x与y的关系,进而可判断.
【解答】解:在Rt△ABC中,∠ACB=90°,AC=BC=2,CD⊥AB于点D,
∴AB=4,点D是AB的中点,∠CDB=∠B=45°;
∴AD=CD=BD=2,
根据点P的运动可知,需要分两种情况,当点P在CD上时,
∴CP=x,
∵PE⊥BC,
∴△PCE是等腰直角三角形,
∴CE=PEx,
∴y x xx2,
∴函数图象是一段抛物线,且开口向上;
当点P在DA上时,如图,
∴OP=x﹣2,BP=2+x﹣2=x,
∵PE⊥BC,
∴△PBE是等腰直角三角形,
∴PE=BEx,
∴CE=2x,
∴y x (2x)x2+x,
∴函数图象是一段抛物线,且开口向下;
故选:B.
【点评】本题考查了动点问题的函数图象,解决本题的关键是掌握二次函数图象的性质.
二.填空题(共5小题)
9.【答案】见试题解答内容
【分析】根据圆的周长表示出半径,再利用圆的面积公式列式整理即可.
【解答】解:∵圆的周长为xcm,
∴圆的半径为cm,
∴圆的面积为y=π()2x2,
即yx2.
故答案为:yx2.
【点评】本题考查了函数关系式,主要利用了圆的周长和面积公式,难点在于用周长表示出圆的半径.
10.【答案】m=0.5n+10(n≤50).
【分析】根据表格得到弹簧原来的长度是10厘米,再算出挂上1克重物弹簧伸长的长度,最后用字母表示出代数式.
【解答】解:弹簧原来的长度:10.5﹣0.5=10(厘米),
挂上1克重物弹簧伸长的长度:0.5÷1=0.5(厘米),
∴m=0.5n+10(n≤50),
故答案为:m=0.5n+10(n≤50).
【点评】本题考查了函数的表示方法,解题的关键是求出弹簧原来的长度和每挂上1克重物弹簧伸长的长度.
11.【答案】28.
【分析】从图2看,y=14=BM,则在BC上运动的时间为:9﹣7=2,即可求解.
【解答】解:从图2看,y=14=BM,
则AB=14,
点M在AB上运动的时间为:14÷2=7,
则在BC上运动的时间为:9﹣7=2,
则BC=2×2=4,
则△ABC的面积AB BC14×4=28,
故答案案为:28.
【点评】本题考查动点的函数图象,面积计算.从函数图象中有效的获取信息,求出AB,BC的长是解题的关键.
12.【答案】18.
【分析】根据题意,分析P的运动路线,分阶段分别进行讨论,可得BC,CD的值,再由梯形的面积公式计算,即可求解.
【解答】解:根据题意,当P在BC上时,
,
此时y随x的增大而增大,
结合图2得:当x=4时,点P与点C重合,
∴BC=4;
当P在CD上时,,
此时y保持不变,
结合图2得:当x=7时,点P与点D重合,
∴CD=7﹣4=3;
∴四边形ABCD的面积为.
故答案为:18.
【点评】此题主要考查矩形的动点问题,解题的关键是根据题意作出辅助线进行求解.
13.【答案】y=﹣2x﹣4.
【分析】根据运算程序求解出y与x之间的关系式.
【解答】解:由题意得,y与x之间的关系式是y=﹣2x﹣4,
故答案为:y=﹣2x﹣4.
【点评】此题考查了运用运算程序求解函数解析式的能力,关键是能准确理解并运用以上知识.
三.解答题(共9小题)
14.【答案】见试题解答内容
【分析】(1)根据图2即可求得点E沿BC向点C运动的过程中的速度,根据速度、路程和时间的关系即可求得BE的长,进而根据三角形面积公式求得y与x的关系式;
(2)把x=2代入关系式即可求得y的值,直线的斜率就是函数的变化率.
【解答】解:(1)由图2可知,在点E沿BC向点C运动的过程中,它的速度是3cm/s,
所以线段BE的长是3xcm;
根据三角形的面积公式得:y3x×8=12x;
故答案为3.3x,y=12x;
(2)当x=2时,y=12×2=24;
由y=12x可知,因为12是斜率,说明x每增加一个单位,y增加12个单位,
所以当x每增加1s时,y增加12cm2,
故答案为24cm2,12cm2.
【点评】本题考查了动点问题的函数图象,三角形的面积,函数的变化和斜率的关系等.
15.【答案】(1)图象见解析过程;
(2);
(3)y1>y2.
【分析】(1)将表格中的各点坐标再平面直角坐标系中描出,再用平滑的曲线连接即可.
(2)根据所画函数图象即可解决问题.
(3)运用数形结合的思想解决问题.
【解答】解:(1)函数图象如图所示,
(2)由(1)所画的函数图象可知,
y是x的反比例函数,
令,
将x=1,y=6代入得,
k=1×6=6.
所以函数表达式为.
(3)由函数图象可知,
当x>0时,y随x的增大而减小,
又0<x1<x2,
所以y1>y2.
【点评】本题考查函数图象及函数关系式,能正确的描点连线,并得出y是x的反比例函数是解题的关键.
16.【答案】(1)10元;
(2)28元;
(3)8元.
【分析】(1)由函数图象可知,购买2千克苹果的总价是20元,据此可得答案;
(2)由题意可得,当x≥2时苹果的单价,进而得出购买3千克苹果需要的价钱;
(3)结合(3)的结论分别求出一次性下单购买苹果6千克与平均分3次下单购买所需费用,即可得出结果.
【解答】解:(1)20÷2=10(元),
答:购买1千克苹果需要10元;
(2)当x≥2时苹果的单价为:(44﹣20)÷(5﹣2)=8(元),
20+8=28(元),
答:购买3千克苹果需要28元;
(3)一次性下单购买苹果6千克需要费用:20+4×8=52(元),
平均分3次下单购买需要费用:20×3=60(元),
60﹣52=8(元),
答:可节省8元.
【点评】本题考查了函数的图象,解答本题明确题意,利用数形结合的思想解答.
17.【答案】(1)11秒;
(2)2.5秒或8.5秒.
【分析】(1)由图2可知,点P运动3秒到达点B,再由点P的运动速度和AB:AD=3:5,即可解决问题.
(2)由(1)中求得的数据,可知矩形的面积,进而可得出点P在BC上运动时,△APD的面积为定值30,再对点P的位置再AB和CD上进行分类即可.
【解答】解:(1)由图2知,
点P运动3秒时到达B点,
又点P的运动速度是2cm/秒,
所以AB=2×3=6cm.
又AB:AD=3:5,
则AD=10cm.
又四边形ABCD是长方形,
所以CD=AB=6cm.
则AB+BC+CD=6+10+6=22cm,
所以22÷2=11秒.
故点P从点A出发,经过11秒后到达点D.
(2)由(1)知,
,
则当点P在BC上运动时,
△ADP的面积恒为:60÷2=30cm2.
又25<30,
则当点P在边AB上时,
25×2÷10=5cm,
5÷2=2.5秒.
当点P在边CD上时,
6+10+6﹣5=17cm,
17÷2=8.5秒.
综上所述,经过2.5秒或8.5秒后三角形APD的面积恰好是25cm2.
【点评】本题考查动点运动的函数图象问题,能根据图2得出AB的长进而求出AD是解题的关键.
18.【答案】(1)①y=2.5x;②3.5x﹣10;(2)15;(3)12.
【分析】(1)①根据不超过10立方米时应缴水费=2.5×用水量;
②超过10立方米时应缴水费=2.5×10+3.5×超出10立方米的用水量,即可得出y关于x的函数关系式;
(2)将x=6代入y=2.5x中,求出y值即可;
(3)根据2.5×10=25(元),32>25,即可得出该户居民月用水量超出10立方米,将y=27代入y=3.5x﹣10中,求出x值即可.
【解答】解:(1)①当0≤x≤10时,y=2.5x;
故答案为:y=2.5x;
②当x>10时,y=2.5×10+3.5(x﹣10)=3.5x﹣10;
故答案为:3.5x﹣10;
(2)当x=6时,y=2.5×6=15(元),
答:应交水费15元;
(3)2.5×10=25(元),32>25,
即可得出该户居民月用水量超出10立方米,
当y=32时,3.5x﹣10=32,
x=12,
答:该户居民用水12立方米.
【点评】本题考查了一次函数的应用,解题的关键是根据题意列出y关于x的函数关系式,再根据函数关系式求值.
19.【答案】(1)540;
(2)(200a+972);
(3)当年用气量不超过360m3时,每年支出的燃气费为2.7x元;当年用气量超过360m3不超过660m3时,每年支出的燃气费为(3.3x﹣216)元;当年用气量超过660m3时,每年支出的燃气费为:(3.8x﹣546)元.
【分析】(1)由于甲用户使用天然气200m3,则直接用第一档的计算方式即可求解;
(2)由于乙用户有5人,则其基数分别调整为不超过360m3,超过360m3不超过660m3,超出660m3,据此进行作答即可;
(3)分三种情况讨论当年用气量不超过360m3时;当年用气量超过360m3不超过660m3时;当年用气量超过660m3时,进行求解即可.
【解答】解:(1)由题意得:2.7×200=540(元),
故答案为:540;
(2)由题意得:2.7×(300+60)+[560﹣(300+60)]a=200a+972,
即应缴费(200a+972)元;
故答案为:(200a+972);
(3)当年用气量不超过360m3时,
每年支出的燃气费为:2.7x元;
当年用气量超过360m3不超过660m3时,
每年支出的燃气费为:2.7×360+3.3(x﹣360)=(3.3x﹣216)元;
当年用气量超过660m3时,
每年支出的燃气费为:2.7×360+3.3×(660﹣360)+(x﹣660)×(3.3+0.5)=(3.8x﹣546)元.
答:当a=3.3时丙用户一年支出的燃气费为(3.8x﹣546)元.
【点评】本题主要考查了列代数式,解答的关键是理解清楚题意,找到其中的数量关系.
20.【答案】(1)﹣18;(2)5500.
【分析】(1)由3000÷1000=3,3×(﹣6)=﹣18,即可得气温变化量为﹣18℃.
(2)由[(﹣27)﹣6]÷(﹣6)×1000=5500 (米),即可得登山运动员攀登了5500 米.
【解答】解:(1)3000÷1000=3(个),
3×(﹣6)=﹣18(℃),
答:气温变化量为﹣18℃.
(2)[(﹣27)﹣6]÷(﹣6)×1000=5500 (米),
答:登山运动员攀登了5500 米.
【点评】本题主要考查了数量变化的规律,解题关键是找到并正确应用规律.
21.【答案】见解析.
【分析】(1)根据图象和题中的条件得到角度,再用相遇问题来求出所用的时间.
(2)根据相遇,追击来解决旋转的时间.
【解答】解:(1)根据图象,y轴上的点是120°,是最大值,也就是没运动时的角度,
所以∠MQN=120°.
观察图象得到运动6秒时,QA,QB两条线重合,所以VQA+VQB20°/s,
因为在最终停止运动,QB运动两个路程,QA运动一个路程,
所以VQB=2VQA,
VQA(VQB+VQA)°/s,
当运动a秒时,QB到QM,
所以a=1209(秒),
当运动b秒时,QB运动到QM,又返回到QN,
所以b=(120×2)18(秒),
即a+b=27(秒).
故答案为:120°,°/s,27秒.
(2)当QA、QB未相遇时,
t=(120﹣40)÷20=4(秒),
当QA、QB相遇后,QB没到QM时,
t=(120+40)÷20=8(秒)
当QA、QB相遇后,且QB到达过QM,
t﹣(t﹣120)=40,
解得t=12,
所以当AOB=40时,t=4s,t=8s,t=12s.
【点评】本题考查了图象与数据之间的关系,关键用路程问题来解决问题.
22.【答案】(1)2.5;
(2)20;
(3)琳琳从邮局走回家的速度是60m/min.
【分析】(1)根据所给图象,结合琳琳的行走路线即可解决问题.
(2)根据所给图象,结合琳琳的行走路线即可解决问题.
(3)由所给图象,得出邮局离琳琳家的距离,再求出所用时间即可解决问题.
【解答】解:(1)由所给图象可知,
药店离琳琳家2.5km,琳琳用了15min走到药店;
因为30﹣15=15(min),
所以琳琳在药店停留了15min;
因为2.5﹣1.5=1(km),45﹣30=15(min),
所以药店距邮局1km,琳琳走了15min;
因为65﹣45=20(min),
所以琳琳在邮局停留了20min;
因为1.5﹣0=1.5(km),90﹣65=25(min),
所以邮局离琳琳家1.5km,琳琳走了25min.
故答案为:2.5.
(2)由(1)知,
琳琳在邮局停留了20min,
即琳琳邮寄物品用了20min.
故答案为:20.
(3)由(1)知,
邮局离琳琳家1.5km,琳琳走了25min,
所以1500÷25=60(m/min),
故琳琳从邮局走回家的速度是60m/min.
【点评】本题考查函数的图象,读懂所给函数图象是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第六章 变量之间的关系
一.选择题(共8小题)
1.在测浮力的实验中,将一长方体石块由玻璃器皿的上方,向下缓慢移动浸入水里的过程中,弹簧测力计的示数F拉力(N)与石块下降的高度x(cm)之间的关系如图所示.(温馨提示:当石块位于水面上方时,F拉力=G重力,当石块入水后,F拉力=C重力﹣F浮力.)则以下说法正确的是( )
A.当石块下降3cm时,此时石块在水里
B.当6≤x≤10时,F拉力(N)与x(cm)之间的函数表达式为F拉力
C.石块下降高度8cm时,此时石块所受浮力是1N
D.当弹簧测力计的示数为3N时,此时石块距离水底
2.甲、乙两车从A城出发前往B城,过程中,汽车离开A城的距离y(km)与时刻t的关系如图所示,则被墨水遮住的时刻是( )
A.7:20 B.7:30 C.7:45 D.8:00
3.某树苗原始高度为60cm,如图是该树苗的高度与生长的月数的有关数据示意图,假设以后一段时间内,该树苗高度的变化与月数保持此关系,用式子表示生长n个月时,它的高度(单位:cm)应为( )
A.60+5(n﹣1) B.60+5n
C.60+10(n﹣1) D.60+10n
4.为了探究浮力的大小与哪些因素有关,方老师带同学们进行了测浮力的实验,如图1,先将一个长方体铁块放在玻璃烧杯上方,再向下缓缓移动,移动过程中记录弹簧测力计的示数与铁块下降的高度之间的关系如图2所示.下列说法不正确的是( )
A.铁块入水之前,烧杯内水的高度为10cm
B.由AB段是线段可知,铁块是匀速向下移动的
C.铁块的高度为4cm
D.当铁块下降的高度为8cm时,该铁块所受到的浮力为3.25N
5.如图,一个正方体的棱长为x cm,它的表面积为y cm2,则y与x的函数关系式为( )
A.y=x2 B.y=3x2 C.y=6x2 D.y=12x2
6.如图①,在△ABC中,∠B=108°,动点P从点A出发,沿折线A→B→C→A匀速运动一周.若点P的运动速度为1cm/s,设点P的运动时间为t(s),AP的长度为v(cm),v与t的函数图象如图②所示.当BP恰好是∠ABC的一条三等分线时,t的值为( )
A.2或5 B.3或6 C.3或5 D.2或6
7.如图1,在等腰Rt△ABC中,∠ACB=90°,CD⊥AB于点D.动点P从点A出发,沿着A→D→C的路径以每秒1个单位长度的速度运动到点C停止,过点P作PE⊥AC于点E,作PF⊥BC于F.在此过程中四边形CEPF的面积y与运动时间x的函数关系图象如图2所示,则AB的长是( )
A.4 B. C. D.3
8.如图,在Rt△ABC中,∠ACB=90°,,CD⊥AB于点D.点P从点C出发,沿C→D→A的路径匀速运动,运动到点A停止,过点P作PE⊥BC于点E,设点P运动的路程为x,△PCE的面积为y,则y与x的函数图象是( )
A.
B.
C.
D.
二.填空题(共5小题)
9.若圆的周长为x cm,该圆的面积为y cm2,则y与x的函数关系式为 .
10.有一根弹簧挂上不超过50克重物后,它的长度会改变,请根据下面表格中的一些数据回答问题:
质量(克) 1 2 3 4 … n
伸长量(厘米) 0.5 1 1.5 2 …
总长度(厘米) 10.5 11 11.5 12 … m
当所挂重物为n克时,弹簧的总长度为m厘米,则m= (用含n的代数式表示).
11.如图①,在Rt△ABC中,∠ABC=90°,动点M从A点运动到B点再到C点后停止,速度为2单位/s,其中BM长y与运动时间x(单位:s)的关系如图②,则△ABC的面积为 .
12.如图1.在四边形ABCD中,AB∥CD,AB=6,AB⊥BC,动点P从点B出发,沿B→C→D→A的方向运动,到达点A停止,设点P运动的路程为x,△ABP的面积为y,如果y与x的函数图象2所示,那么四边形ABCD的面积为 .
13.在如图所示的计算程序中,输入一个有理数x,便可输出一个相应的有理数y,则y与x之间的关系式是 .
三.解答题(共9小题)
14.如图1,AD是三角形ABC的边BC上的高,且AD=8cm,BC=9cm,点E从点B出发,沿线段BC向终点C运动,其速度与时间的关系如图2所示,设点E运动时间为x(s),三角形ABE的面积为y(cm2).
(1)在点E沿BC向点C运动的过程中,它的速度是 cm/s,用含x的代数式表示线段BE的长是 cm,变量y与x之间的关系式为 ;
(2)当x=2时,y的值为 ;当x每增加1s时,y的变化情况是: .
15.经过实验获得两个变量x(x>0),y(y>0)的一组对应值如表.
x 1 2 3 4 5
y 6 3 2 1.5 1.2
(1)请在如图所示的平面直角坐标系中画出相应函数的图象;
(2)求出函数表达式;
(3)点A(x1,y2),B(x2,y2)在此函数图象上,若0<x1<x2,则y1,y2有怎样的大小关系?
16.某网上购物平台促销,苹果2千克以上有优惠(不含2千克),购买苹果所付金额(元)与购买数量(千克)之间的关系如图所示,根据图象回答下列问题:
(1)购买1千克苹果多少元?
(2)购买3千克苹果多少元?
(3)一次性下单购买苹果6千克与平均分3次下单购买可节省多少元?
17.如图1,在长方形ABCD中,AB:AD=3:5,点P从点A出发以2cm/秒的速度沿A→B→C→D的路线匀速移动.随着点P的移动,三角形APD的面积会不断发生变化,它的面积变化情况如图2所示.
(1)点P从点A出发,经过多少秒后到达点D?
(2)点P从点A出发,经过多少秒后三角形APD的面积恰好是25cm2?
18.某市为了节约用水,采用分段收费标准,设居民每月应交水费为y(元),用水量为x(立方米).
用水量(立方米) 收费(元)
不超过10立方米 每立方米2.5元
超过10立方米 超过的部分每立方米3.5元
(1)写出每月用水量不超过10立方米和超过10立方米时,水费与用水量之间的关系式:
①每月用水量不超过10立方米时,y= ;
②每月用水量超过10立方米时,y= ;
(2)若某户居民某月用水量为6立方米,则应交水费多少元?
(3)若某户居民某月交水费32元,则该户居民用水多少立方米?
19.为增强公民的节约意识,合理利用天然气资源,我市将居民用天然气用气量及价格分为三档,其中:
档次 年用气量 单价(元/m3)
第一档气量 不超出300m3的部分 2.7
第二档气量 超出300m3不超出600m3的部分 a
第三档气量 超出600m3的部分 a+0.5
(说明:户籍人口超过4人的家庭,每增加1人,各档年用气量基数按每人增加60立方米依次调整)
(1)若甲用户户籍人口登记有4人,今年前三个月已使用天然气200m3,则应缴费 元.
(2)若乙用户户籍人口登记有5人,今年已使用天然气560m3,则应缴费 元.(用含a的代数式表示)
(3)若丙用户户籍人口登记有5人,今年该用户年用气量为x(m3),当a=3.3时请用含x的代数式表示丙用户一年支出的燃气费.
20.根据实验测定:高度每增加1000米,气温大约变化量为﹣6℃.
(1)若某登山运动员攀登了3000米,则气温变化量为多少?
(2)若某登山运动员在攀登途中发回信息,报告他所在高度的气温为﹣27℃,如果当时地面温度为6℃,求此时该登山运动员攀登了多少米?
21.如图1,已知∠MQN,QA、QB分别从QM、QN同时开始旋转,QA按逆时针方向旋转,旋转到与QN重合时停止旋转,QB按顺时针方向旋转,旋转到与QM重合后,立刻按原速度逆时针返回,与QN重合停止旋转.根据观察,QA、QB最终同时停止旋转,旋转过程中∠AQB的大小记作y(°),旋转时间记作t(s),y与t之间的关系如图2所示.
(1)依据图象,请直接填写:∠MQN= °;QA旋转的速度是 °/s;a+b= ;
(2)当∠AQB=40°时,求旋转时间t的值.
22.已知琳琳家、药店、邮局在同一直线上,琳琳从家出发,跑步去药店买了酒精和口罩,又步行到邮局把物品寄出,然后走回家.琳琳离家的距离y(km)与时间x(min)之间的关系如图所示,请根据图象解决下列问题:
(1)琳琳家离药店的距离为 km;
(2)琳琳邮寄物品用了 min;
(3)求琳琳从邮局走回家的速度是多少?
第六章 变量之间的关系
参考答案与试题解析
一.选择题(共8小题)
1.【答案】D
【分析】观察图象,解出6≤x10的函数关系式,利用关系式判断出相关结论即可解题.
【解答】解:A、由图得,当石块下降3cm时,拉力不变,此时石块不在水里,故A不符题意;
B、设F=kx+b,代入(6,4)(10,2.5),得Fx,故B不符合题意;
C、将x=8代入Fx,得F,4,故C不符合题意;
D、将F=3代入Fx,得x,16,故D符合题意;
故选:D.
【点评】本题考查了函数图象的应用,对物理常识的掌握及数形结合的思想是解题关键.
2.【答案】B
【分析】根据题意可得甲和乙的速度,据此可得乙追上甲的数据,进而得出答案.
【解答】解:甲的速度为:300÷(10﹣5)=60(km/h),
乙的速度为:300÷(9﹣6)=100(km/h),
设乙用了x小时追上甲,根据题意得:
100x=60×(x+1),
解得x=1.5,
即乙用了1.5小时追上甲,
所以被墨水遮住的时刻是7:30.
故选:B.
【点评】本题考查了函数的图象.主要利用了路程、速度、时间三者之间的关系,准确识图,理解横、纵坐标的实际意义是解题的关键.
3.【答案】D
【分析】由题意可得树苗每个月增长的高度是10cm,进而得出答案.
【解答】解:根据题意可得,树苗每个月增长的高度是10cm,
∴用式子表示生长n个月时,它的高度(单位:cm)应为:(60+10n)cm.
故选:D.
【点评】本题考查了函数的图象,得出树苗每个月增长的高度是解答本题的关键.
4.【答案】D
【分析】图2中点(0,4)表示铁块未移动时,拉力为4N,那么铁块的重力为4N,此时铁块下表面与烧杯上端平齐;(6,4)表示铁块向下移动6cm时,拉力为4N,此时铁块下表面与水面平齐;铁块继续向下移动,水向外流出,水平面保持不变.(10,2.5)表示铁块上表面刚好浸入水中,拉力为2.5N.烧杯高度为16cm,铁块下表面接触水时移动了6cm,所以烧杯内水的高度为10cm,可判断A正确,不符合题意;由AB段是线段可知,拉力与移动的距离成一次函数关系,铁块是匀速向下移动的,可判断B正确,不符合题意;AB段表示铁块下表面刚接触水到铁块上表面刚好浸入水中的过程,因为水平面保持不变.那么AB段铁块移动的距离即为铁块的高度,为10﹣6等于4cm,可判断C正确,不符合题意;当铁块下降高度为8cm时,由于出水口的存在,由图2和B选项可知,铁块的一半刚好浸入水中,拉力的大小为3.25N,那么所受到的浮力=重力﹣拉力=4﹣3.25=0.75N,故D错误,符合题意.
【解答】解:∵烧杯高度为16cm,铁块从烧杯口到下表面接触水时移动了6cm,∴烧杯内水的高度为10cm,故A正确,不符合题意;
∵AB段是线段,∴拉力与移动的距离成一次函数关系,∴铁块是匀速向下移动的,故B正确,不符合题意;
∵烧杯有出水口,∴水平面在铁块下移过程中保持不变.∴铁块的高度为AB段铁块移动的距离为10﹣6=4cm,故C正确,不符合题意;
∵当铁块下降高度为8cm时,铁块的一半刚好浸入水中,∴拉力的大小为3.25N,∵铁块的重力为4N,∴铁块所受到的浮力为4﹣3.25=0.75N,故D错误,符合题意.
故选:D.
【点评】本题考查动点问题的函数图象.关键是得到图象中关键点表示的意义.用到的知识点为:浮力=重力﹣拉力.
5.【答案】C
【分析】正方体有6个面,每一个面都是边长为x的正方形,这6个正方形的面积和就是该正方体的表面积.
【解答】解:由题意得,y=6x2,
故选:C.
【点评】本题考查函数关系式,理解两个变量之间的关系是得出关系式的关键.
6.【答案】B
【分析】根据图②可知,AB=BC=2,再根据BP,BP′是∠ABC的三等分线,可以证明△PBC∽△BAC,求出PC的长,即可求出答案.
【解答】解:如图①,BP,BP′是∠ABC的三等分线,
根据图②可知,AB=BC=2,
∵∠ABC=108°,AB=BC,
∴∠A=∠C=∠ABP′=∠CBP=∠PBP′=36°,
∴∠APB=∠ABP=72°,
∴AB=AP=2,
同理CP′=BC=2,
∵∠PBC=∠A,∠C=∠C,
∴△PBC∽△BAC,
∴,
∴,
∴PC1或1(负值舍去),
∴AB+BC+PC3,AB+BC+CP′=6,
∴当BP恰好是∠ABC的一条三等分线时,t的值为3或6.
故选:B.
【点评】本题是动点问题的函数图象,考查了等腰三角形的性质,相似三角形的判定和性质,证明三角形相似是解题的关键.
7.【答案】B
【分析】图2中拐点的纵坐标3,即四边形CEPF的面积y=3,此时点P运动到点D.可证明四边形CEPF是正方形,面积为3,那么正方形的边长AP为.易得△AEP为等腰直角三角形,所以AP长,那么可得AB长度为2.
【解答】解:∵动点P从点A出发,沿着A→D→C的路径运动,
∴第一个拐点的位置在点D处,此时点P运动到点D.
∵图2中拐点的纵坐标3,
∴四边形CEPF的面积为3.
∵PE⊥AC,PF⊥BC,
∴∠CED=∠CFD=∠AED=90°.
∵∠ACB=90°,
∴四边形CEPF是矩形.
∵△ABC是等腰直角三角形,CD⊥AB,
∴∠ACD=∠BCD,∠A=45°,AB=2AP.
∴DE=DF,∠ADE=45°
∴四边形CEPF是正方形,AE=PE.
∴△AED是等腰直角三角形.
∵四边形CEPF的面积为3,
∴PE.
∴AP.
∴AB=2AP=2.
故选:B.
【点评】本题考查了动点问题的函数图象.关键是得到拐点的纵坐标表示的意义及动点此时所在的位置.用到的知识点为:等腰直角三角形的斜边长=直角边边长的倍.
8.【答案】B
【分析】根据题意可知,需要分两种情况,当点P在CD上时,当点P在DA上时,根据三角形的面积公式可得出x与y的关系,进而可判断.
【解答】解:在Rt△ABC中,∠ACB=90°,AC=BC=2,CD⊥AB于点D,
∴AB=4,点D是AB的中点,∠CDB=∠B=45°;
∴AD=CD=BD=2,
根据点P的运动可知,需要分两种情况,当点P在CD上时,
∴CP=x,
∵PE⊥BC,
∴△PCE是等腰直角三角形,
∴CE=PEx,
∴y x xx2,
∴函数图象是一段抛物线,且开口向上;
当点P在DA上时,如图,
∴OP=x﹣2,BP=2+x﹣2=x,
∵PE⊥BC,
∴△PBE是等腰直角三角形,
∴PE=BEx,
∴CE=2x,
∴y x (2x)x2+x,
∴函数图象是一段抛物线,且开口向下;
故选:B.
【点评】本题考查了动点问题的函数图象,解决本题的关键是掌握二次函数图象的性质.
二.填空题(共5小题)
9.【答案】见试题解答内容
【分析】根据圆的周长表示出半径,再利用圆的面积公式列式整理即可.
【解答】解:∵圆的周长为xcm,
∴圆的半径为cm,
∴圆的面积为y=π()2x2,
即yx2.
故答案为:yx2.
【点评】本题考查了函数关系式,主要利用了圆的周长和面积公式,难点在于用周长表示出圆的半径.
10.【答案】m=0.5n+10(n≤50).
【分析】根据表格得到弹簧原来的长度是10厘米,再算出挂上1克重物弹簧伸长的长度,最后用字母表示出代数式.
【解答】解:弹簧原来的长度:10.5﹣0.5=10(厘米),
挂上1克重物弹簧伸长的长度:0.5÷1=0.5(厘米),
∴m=0.5n+10(n≤50),
故答案为:m=0.5n+10(n≤50).
【点评】本题考查了函数的表示方法,解题的关键是求出弹簧原来的长度和每挂上1克重物弹簧伸长的长度.
11.【答案】28.
【分析】从图2看,y=14=BM,则在BC上运动的时间为:9﹣7=2,即可求解.
【解答】解:从图2看,y=14=BM,
则AB=14,
点M在AB上运动的时间为:14÷2=7,
则在BC上运动的时间为:9﹣7=2,
则BC=2×2=4,
则△ABC的面积AB BC14×4=28,
故答案案为:28.
【点评】本题考查动点的函数图象,面积计算.从函数图象中有效的获取信息,求出AB,BC的长是解题的关键.
12.【答案】18.
【分析】根据题意,分析P的运动路线,分阶段分别进行讨论,可得BC,CD的值,再由梯形的面积公式计算,即可求解.
【解答】解:根据题意,当P在BC上时,
,
此时y随x的增大而增大,
结合图2得:当x=4时,点P与点C重合,
∴BC=4;
当P在CD上时,,
此时y保持不变,
结合图2得:当x=7时,点P与点D重合,
∴CD=7﹣4=3;
∴四边形ABCD的面积为.
故答案为:18.
【点评】此题主要考查矩形的动点问题,解题的关键是根据题意作出辅助线进行求解.
13.【答案】y=﹣2x﹣4.
【分析】根据运算程序求解出y与x之间的关系式.
【解答】解:由题意得,y与x之间的关系式是y=﹣2x﹣4,
故答案为:y=﹣2x﹣4.
【点评】此题考查了运用运算程序求解函数解析式的能力,关键是能准确理解并运用以上知识.
三.解答题(共9小题)
14.【答案】见试题解答内容
【分析】(1)根据图2即可求得点E沿BC向点C运动的过程中的速度,根据速度、路程和时间的关系即可求得BE的长,进而根据三角形面积公式求得y与x的关系式;
(2)把x=2代入关系式即可求得y的值,直线的斜率就是函数的变化率.
【解答】解:(1)由图2可知,在点E沿BC向点C运动的过程中,它的速度是3cm/s,
所以线段BE的长是3xcm;
根据三角形的面积公式得:y3x×8=12x;
故答案为3.3x,y=12x;
(2)当x=2时,y=12×2=24;
由y=12x可知,因为12是斜率,说明x每增加一个单位,y增加12个单位,
所以当x每增加1s时,y增加12cm2,
故答案为24cm2,12cm2.
【点评】本题考查了动点问题的函数图象,三角形的面积,函数的变化和斜率的关系等.
15.【答案】(1)图象见解析过程;
(2);
(3)y1>y2.
【分析】(1)将表格中的各点坐标再平面直角坐标系中描出,再用平滑的曲线连接即可.
(2)根据所画函数图象即可解决问题.
(3)运用数形结合的思想解决问题.
【解答】解:(1)函数图象如图所示,
(2)由(1)所画的函数图象可知,
y是x的反比例函数,
令,
将x=1,y=6代入得,
k=1×6=6.
所以函数表达式为.
(3)由函数图象可知,
当x>0时,y随x的增大而减小,
又0<x1<x2,
所以y1>y2.
【点评】本题考查函数图象及函数关系式,能正确的描点连线,并得出y是x的反比例函数是解题的关键.
16.【答案】(1)10元;
(2)28元;
(3)8元.
【分析】(1)由函数图象可知,购买2千克苹果的总价是20元,据此可得答案;
(2)由题意可得,当x≥2时苹果的单价,进而得出购买3千克苹果需要的价钱;
(3)结合(3)的结论分别求出一次性下单购买苹果6千克与平均分3次下单购买所需费用,即可得出结果.
【解答】解:(1)20÷2=10(元),
答:购买1千克苹果需要10元;
(2)当x≥2时苹果的单价为:(44﹣20)÷(5﹣2)=8(元),
20+8=28(元),
答:购买3千克苹果需要28元;
(3)一次性下单购买苹果6千克需要费用:20+4×8=52(元),
平均分3次下单购买需要费用:20×3=60(元),
60﹣52=8(元),
答:可节省8元.
【点评】本题考查了函数的图象,解答本题明确题意,利用数形结合的思想解答.
17.【答案】(1)11秒;
(2)2.5秒或8.5秒.
【分析】(1)由图2可知,点P运动3秒到达点B,再由点P的运动速度和AB:AD=3:5,即可解决问题.
(2)由(1)中求得的数据,可知矩形的面积,进而可得出点P在BC上运动时,△APD的面积为定值30,再对点P的位置再AB和CD上进行分类即可.
【解答】解:(1)由图2知,
点P运动3秒时到达B点,
又点P的运动速度是2cm/秒,
所以AB=2×3=6cm.
又AB:AD=3:5,
则AD=10cm.
又四边形ABCD是长方形,
所以CD=AB=6cm.
则AB+BC+CD=6+10+6=22cm,
所以22÷2=11秒.
故点P从点A出发,经过11秒后到达点D.
(2)由(1)知,
,
则当点P在BC上运动时,
△ADP的面积恒为:60÷2=30cm2.
又25<30,
则当点P在边AB上时,
25×2÷10=5cm,
5÷2=2.5秒.
当点P在边CD上时,
6+10+6﹣5=17cm,
17÷2=8.5秒.
综上所述,经过2.5秒或8.5秒后三角形APD的面积恰好是25cm2.
【点评】本题考查动点运动的函数图象问题,能根据图2得出AB的长进而求出AD是解题的关键.
18.【答案】(1)①y=2.5x;②3.5x﹣10;(2)15;(3)12.
【分析】(1)①根据不超过10立方米时应缴水费=2.5×用水量;
②超过10立方米时应缴水费=2.5×10+3.5×超出10立方米的用水量,即可得出y关于x的函数关系式;
(2)将x=6代入y=2.5x中,求出y值即可;
(3)根据2.5×10=25(元),32>25,即可得出该户居民月用水量超出10立方米,将y=27代入y=3.5x﹣10中,求出x值即可.
【解答】解:(1)①当0≤x≤10时,y=2.5x;
故答案为:y=2.5x;
②当x>10时,y=2.5×10+3.5(x﹣10)=3.5x﹣10;
故答案为:3.5x﹣10;
(2)当x=6时,y=2.5×6=15(元),
答:应交水费15元;
(3)2.5×10=25(元),32>25,
即可得出该户居民月用水量超出10立方米,
当y=32时,3.5x﹣10=32,
x=12,
答:该户居民用水12立方米.
【点评】本题考查了一次函数的应用,解题的关键是根据题意列出y关于x的函数关系式,再根据函数关系式求值.
19.【答案】(1)540;
(2)(200a+972);
(3)当年用气量不超过360m3时,每年支出的燃气费为2.7x元;当年用气量超过360m3不超过660m3时,每年支出的燃气费为(3.3x﹣216)元;当年用气量超过660m3时,每年支出的燃气费为:(3.8x﹣546)元.
【分析】(1)由于甲用户使用天然气200m3,则直接用第一档的计算方式即可求解;
(2)由于乙用户有5人,则其基数分别调整为不超过360m3,超过360m3不超过660m3,超出660m3,据此进行作答即可;
(3)分三种情况讨论当年用气量不超过360m3时;当年用气量超过360m3不超过660m3时;当年用气量超过660m3时,进行求解即可.
【解答】解:(1)由题意得:2.7×200=540(元),
故答案为:540;
(2)由题意得:2.7×(300+60)+[560﹣(300+60)]a=200a+972,
即应缴费(200a+972)元;
故答案为:(200a+972);
(3)当年用气量不超过360m3时,
每年支出的燃气费为:2.7x元;
当年用气量超过360m3不超过660m3时,
每年支出的燃气费为:2.7×360+3.3(x﹣360)=(3.3x﹣216)元;
当年用气量超过660m3时,
每年支出的燃气费为:2.7×360+3.3×(660﹣360)+(x﹣660)×(3.3+0.5)=(3.8x﹣546)元.
答:当a=3.3时丙用户一年支出的燃气费为(3.8x﹣546)元.
【点评】本题主要考查了列代数式,解答的关键是理解清楚题意,找到其中的数量关系.
20.【答案】(1)﹣18;(2)5500.
【分析】(1)由3000÷1000=3,3×(﹣6)=﹣18,即可得气温变化量为﹣18℃.
(2)由[(﹣27)﹣6]÷(﹣6)×1000=5500 (米),即可得登山运动员攀登了5500 米.
【解答】解:(1)3000÷1000=3(个),
3×(﹣6)=﹣18(℃),
答:气温变化量为﹣18℃.
(2)[(﹣27)﹣6]÷(﹣6)×1000=5500 (米),
答:登山运动员攀登了5500 米.
【点评】本题主要考查了数量变化的规律,解题关键是找到并正确应用规律.
21.【答案】见解析.
【分析】(1)根据图象和题中的条件得到角度,再用相遇问题来求出所用的时间.
(2)根据相遇,追击来解决旋转的时间.
【解答】解:(1)根据图象,y轴上的点是120°,是最大值,也就是没运动时的角度,
所以∠MQN=120°.
观察图象得到运动6秒时,QA,QB两条线重合,所以VQA+VQB20°/s,
因为在最终停止运动,QB运动两个路程,QA运动一个路程,
所以VQB=2VQA,
VQA(VQB+VQA)°/s,
当运动a秒时,QB到QM,
所以a=1209(秒),
当运动b秒时,QB运动到QM,又返回到QN,
所以b=(120×2)18(秒),
即a+b=27(秒).
故答案为:120°,°/s,27秒.
(2)当QA、QB未相遇时,
t=(120﹣40)÷20=4(秒),
当QA、QB相遇后,QB没到QM时,
t=(120+40)÷20=8(秒)
当QA、QB相遇后,且QB到达过QM,
t﹣(t﹣120)=40,
解得t=12,
所以当AOB=40时,t=4s,t=8s,t=12s.
【点评】本题考查了图象与数据之间的关系,关键用路程问题来解决问题.
22.【答案】(1)2.5;
(2)20;
(3)琳琳从邮局走回家的速度是60m/min.
【分析】(1)根据所给图象,结合琳琳的行走路线即可解决问题.
(2)根据所给图象,结合琳琳的行走路线即可解决问题.
(3)由所给图象,得出邮局离琳琳家的距离,再求出所用时间即可解决问题.
【解答】解:(1)由所给图象可知,
药店离琳琳家2.5km,琳琳用了15min走到药店;
因为30﹣15=15(min),
所以琳琳在药店停留了15min;
因为2.5﹣1.5=1(km),45﹣30=15(min),
所以药店距邮局1km,琳琳走了15min;
因为65﹣45=20(min),
所以琳琳在邮局停留了20min;
因为1.5﹣0=1.5(km),90﹣65=25(min),
所以邮局离琳琳家1.5km,琳琳走了25min.
故答案为:2.5.
(2)由(1)知,
琳琳在邮局停留了20min,
即琳琳邮寄物品用了20min.
故答案为:20.
(3)由(1)知,
邮局离琳琳家1.5km,琳琳走了25min,
所以1500÷25=60(m/min),
故琳琳从邮局走回家的速度是60m/min.
【点评】本题考查函数的图象,读懂所给函数图象是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
